基于内禀模态奇异值熵的声发射管道泄漏诊断

袁培龙，周绍骑，周颖涛，张医帆，唐 航

(1.中国人民解放军后勤工程学院 军事供油工程系，重庆 401331； 2. 68101部队，陕西)



基于内禀模态奇异值熵的声发射管道泄漏诊断

袁培龙1，周绍骑1，周颖涛2，张医帆2，唐 航1

(1.中国人民解放军后勤工程学院 军事供油工程系，重庆 401331； 2. 68101部队，陕西)

管道泄漏诊断是泄漏定位的前提，为诊断管道是否泄漏，针对管道泄漏状态下声发射信号非平稳随机性的特点，提出了基于内禀模态奇异值熵的声发射管道泄漏诊断方法。该方法用EMD分解声发射信号得到内禀模态函数，将内禀模态函数组成初始特征向量，求得奇异值熵，通过对比奇异值熵的大小诊断管道有无泄漏。计算机模拟仿真验证了该方法的有效性，实验结果表明该方法可以准确诊断管道有无泄漏。

内禀模态函数；奇异值熵；管道泄漏；声发射

管道在输送油气过程中泄漏时有发生。在发生泄漏后如果不能及时发现和处理，将造成严重的人员伤亡、经济损失和环境污染。传统的管道泄漏诊断方法，如漏磁检测法、流量平衡法、光纤检测法、负压波法等存在不能连续检测、灵敏度低、价格昂贵等缺点[1-5]。声发射检测法是一种新型的无损检测技术，通过管道声发射信号的特征进行缺陷诊断并预测声发射源的位置，具有加载速度快、适应性强、安全性高的优点。但是声发射信号中也包含了大量的噪声信号。针对管道泄漏声发射信号的非平稳性，本文提出了一种基于内禀模态奇异值熵的声发射管道泄漏诊断方法，运用内禀模态函数和奇异值熵相结合的方法，分析管壁的声发射信号，判断管道泄漏与否。该方法不仅适用于突然泄漏的情况，也适用于已经泄漏的情况，具有一定的应用价值[6-7]。

1 基于内禀模态奇异值熵的理论

1.1 经验模态分解

1998年，美籍华人Norden E.Huang等[9]提出了将任意信号分解为一组本征模态函数(intrinsic mode function,IMF)的新方法——经验模态分解(empirical model decomposition，EMD)。经验模态分解通常是将原始信号分解为若干个本征模态函数，具有很好的自适应性，在分解过程中保持了信号本身的特性，适应于声发射信号等非平稳信号的分析，近年来被大量应用于机械故障诊断和语音信号识别等领域。本征模态函数来自于声发射信号的原始信号，并按照信号的频率的高低顺序排列，反映信号的内在信息。

1.2 信号的奇异值分解

信号的奇异值分解得到的奇异值可以反映信号的内在信息，但在实际应用中需要将信号分段处理组成分段矩阵，这种处理一定程度上降低了信号处理的自适应性。将信号的经验模态分解得到的本征模态函数组成初始矩阵，与信号的奇异值分解相结合，既保持了信号的自适应性，同时也发挥了信号的奇异值分解的优势。

设有N行M列的矩阵A，对它可以进行如下分解，称为奇异值分解[10]，即

A=UΣVT

(1)

式中：U=[u1…uN]∈RN×N；UTU=1；V=[v1…vM]∈RM×M；VTV=1；Σ∈RN×M为矩阵⎣diag{σ1,…,σp}:0」或者其转置的形式，p=min(N,M)，σ1≥…≥σp≥0，σ1,…,σp称为矩阵A的奇异值。

1.3 奇异值熵

在对声发射信号处理过程中，采用经验模态分解与信号的奇异值分解相结合的方法所得到的奇异值的数量较小。因此，可尝试采用信息熵的方法计算奇异值的熵，反映奇异值分布的均匀性，进而分析声发射信号的内在特征。

将熵的概念引入信息论中，对于一个信息源a={a1,a2,…,an}，进行归一化处理q=a/∑a，则a的信息熵的计算公式为：

(2)

根据信息熵的基本性质，式中qi分布越均匀，s(q)越大，反之s(q)越小。将信息熵引入奇异值的分析，将矩阵的奇异值σ={σ1,…,σp}看作一组信息源，进行归一化后通过式(2)即可求出其奇异值的熵。

1.4 基于内禀模态奇异值熵的声发射泄漏诊断

管道泄漏时采集的声发射信号具有一定的背景噪音，实际采集的数据量往往很大，直接进行分析计算量大且量化困难。为使泄漏诊断更加简洁，本文提出了基于内禀模态奇异值熵的管道泄漏诊断方法，其框图如图1所示。

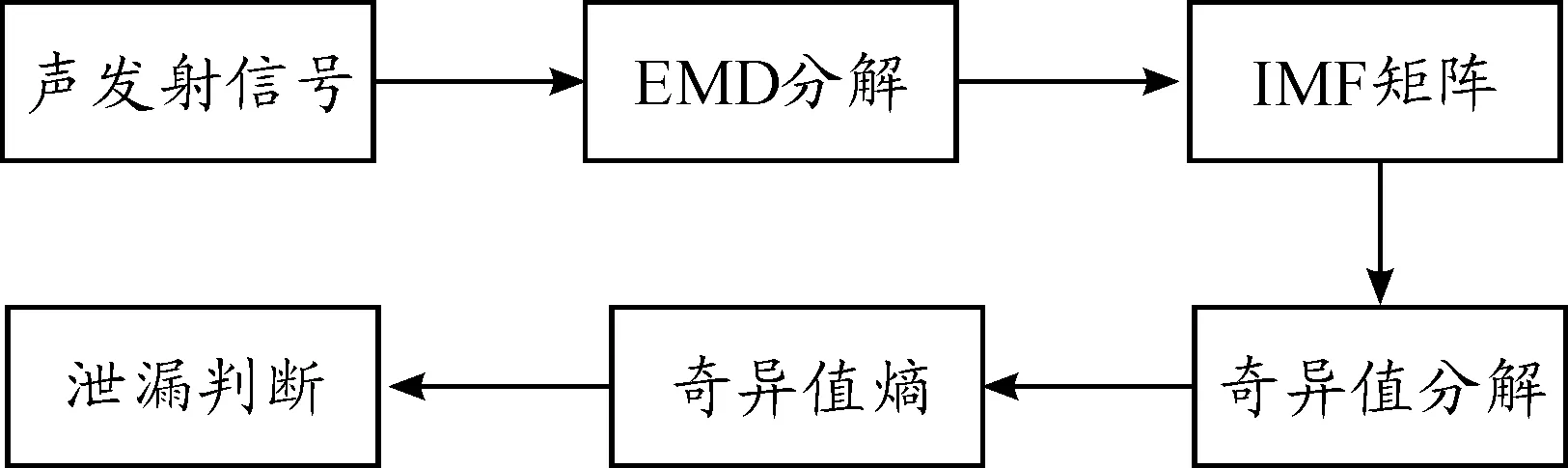
图1 基于内禀模态奇异值熵的管道泄漏诊断方法框图

具体步骤如下：

1) 采集管道在运行状态下的声发射信号。

2) 对声发射信号进行EMD分解，得到一组内禀模态函数IMF1～IMFn，由内禀模态函数组成特征向量矩阵A=[IMF1,…,IMFn]T。

3) 运用matlab的svd函数对矩阵A进行奇异值分解，得到奇异值σ。

4) 对奇异值σ进行归一化，运用信息熵的计算公式，求出奇异值熵。

5)通过对信号的奇异值的大小和奇异值熵进行分析，判断管道有无泄漏。

根据矩阵理论，矩阵的奇异值是矩阵的固有特征，它具有较好的稳定性，即当矩阵元素发生小的变动时，矩阵奇异值变化很小，同时矩阵奇异值还具有旋转不变性和比例不变性，能有效地刻画信号序列的内在特征。EMD分解是自适应的，在较大程度上保持了信号的自身特性，适用于管道泄漏声发射信号等非平稳信号的分析。将信号进行EMD分解得到的IMF组成矩阵，之后进行奇异值分解，避免了将信号直接进行截取组成矩阵时截取长度会发生变化，使得到的奇异值序列具有多个数值。此时得到的计算结果可以直接对信号的奇异值进行分析，通过比较其大小来判断有无泄漏。由于泄漏时的信号强于非泄漏时的信号，泄漏信号的奇异值往往较大。为使结果更加简明，将信息熵引入奇异值的分析，得到奇异值熵，由于管道泄漏时的声发射信号主要由泄漏信号组成，具有非平稳特性，且能量在频域分布较为集中，因此所得到的奇异值熵较小。管道无泄漏时信号主要由背景噪音组成，在频域和时域分布较均匀，所得到的奇异值熵较大。

2 基于内禀模态奇异值熵的计算机仿真验证

x(n)为均值为0、方差为1、长度为1 000的高斯白噪声序列，y(n)=x(n)+2sin(20πt)。运用本文的方法，分别将x(n)和y(n)进行EMD分解，计算奇异值，求取奇异值熵。奇异值结果如图2所示。

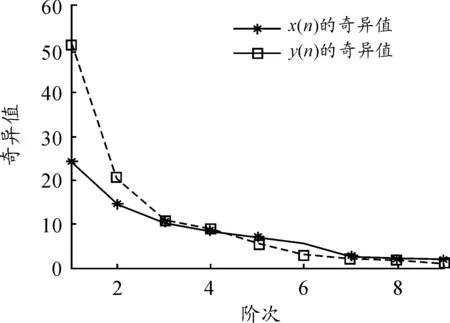
图2 模拟信号的奇异值对比

计算得x(n)的奇异值熵为1.908 6，y(n)的奇异值熵为1.596 8。从图2可以看出：y(n)的奇异值均值大于x(n)的奇异值均值，这是由于信号y(n)的幅值大于x(n)的幅值，奇异值的大小又反映了信号的内在特性。信号x(n)为高斯白噪声，在时域和频域分布较为均匀。信号y(n)中存在一组正弦信号，打破了高斯白噪声在时域和频域分布的均匀性，因此y(n)的奇异值熵小于x(n)，与计算结果相符。

3 基于内禀模态奇异值熵声发射信号实验分析

模拟管道铺设了野战输油管线进行输水实验，管道外径102 mm，壁厚2.5 mm，管材为10号带钢，管内水压为0.18 MPa。采用德国Vallen公司生产的AMSY-5(M16-2)型16通道声发射仪采集信号，采样频率设为2 MHz，增益为40 dB，采样阈值为32 dB。分别采集距离泄漏孔2.0 m和26.8 m处无泄漏和有泄漏时的管壁声发射信号。采集数据均为10组，每组数据长度为5 000。图3和图4为距离泄漏孔不同距离处有无泄漏状态下的声发射信号。

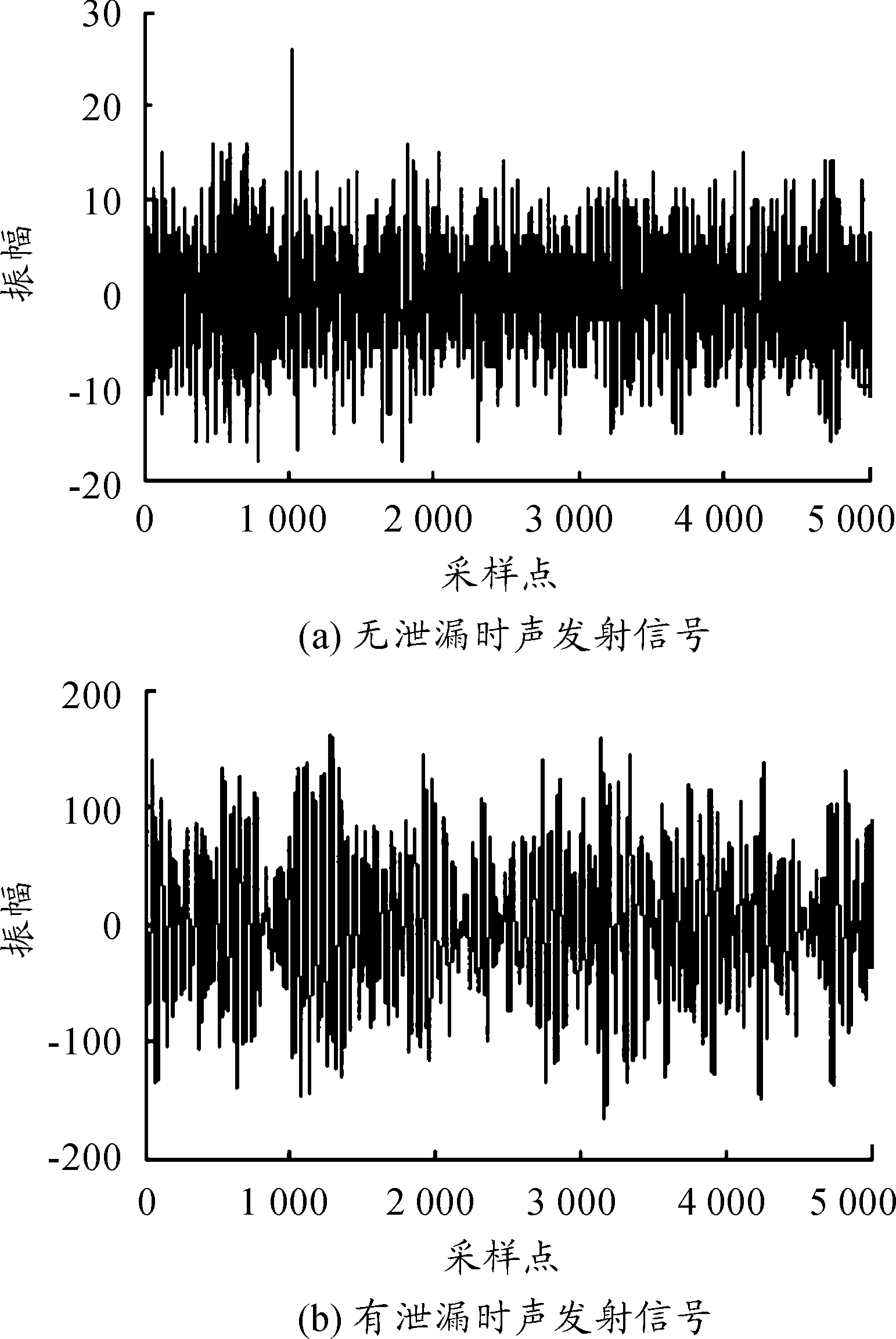
图3 距离泄漏孔26.8 m处的声发射信号

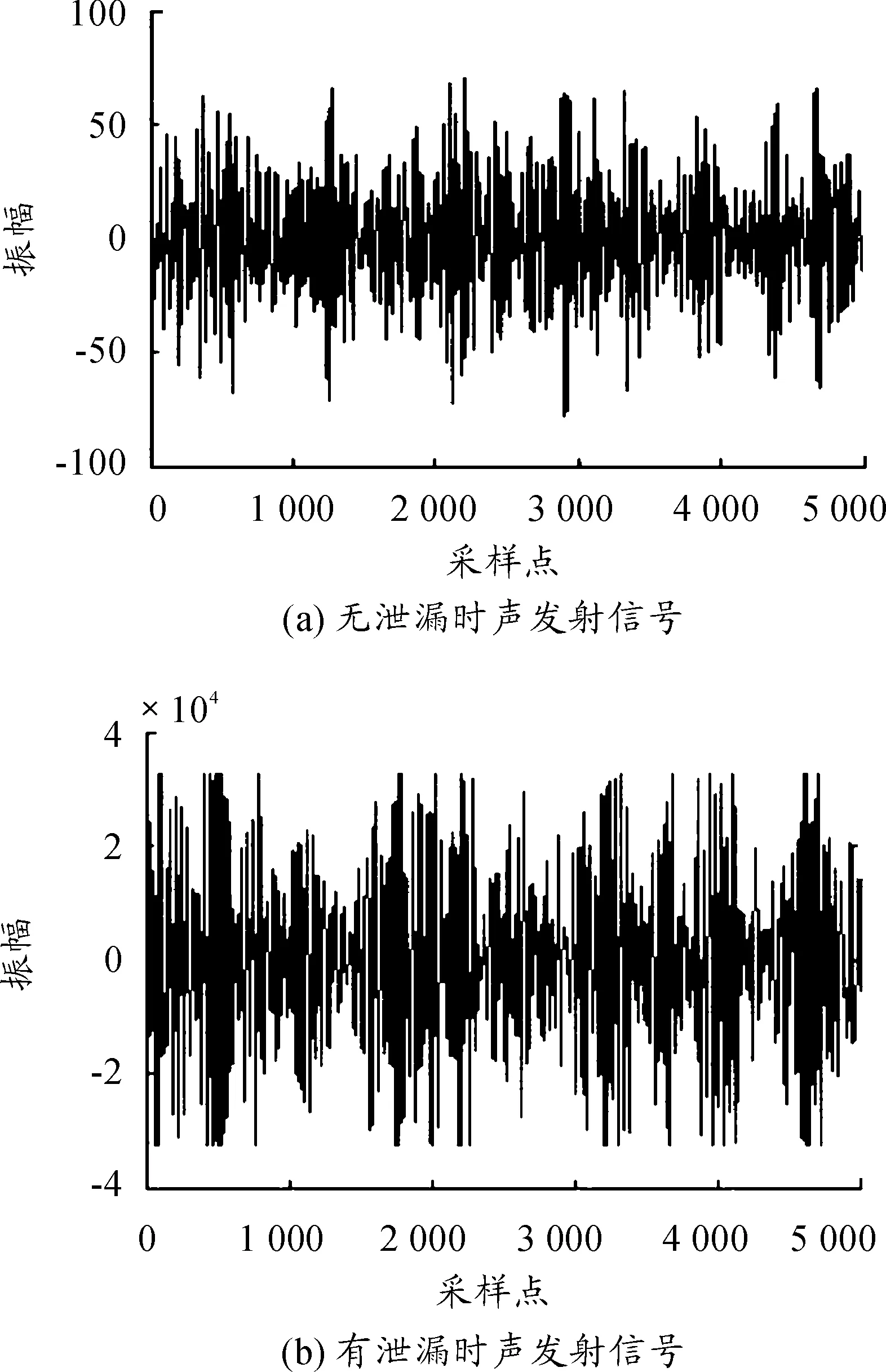
图4 距离泄漏孔2.0 m处的声发射信号

对声发射信号求奇异值，图5和图6为其奇异值计算结果。

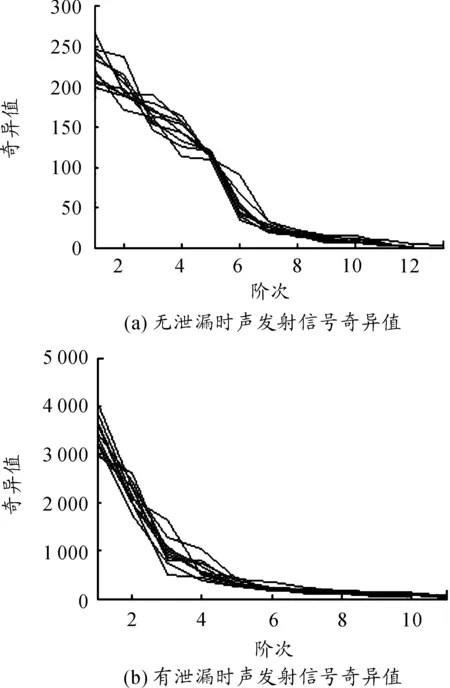
图5 距离泄漏孔26.8 m处的奇异值对比

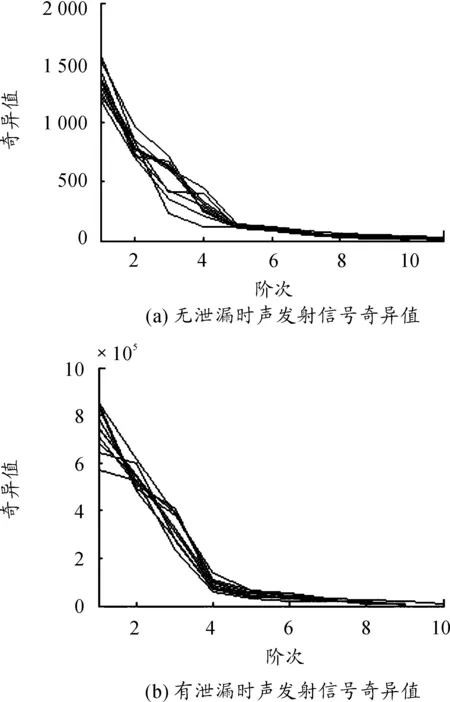
图6 距离泄漏孔2.0 m处的奇异值对比

进一步计算出不同距离两种状态下奇异值熵，如表1所示。

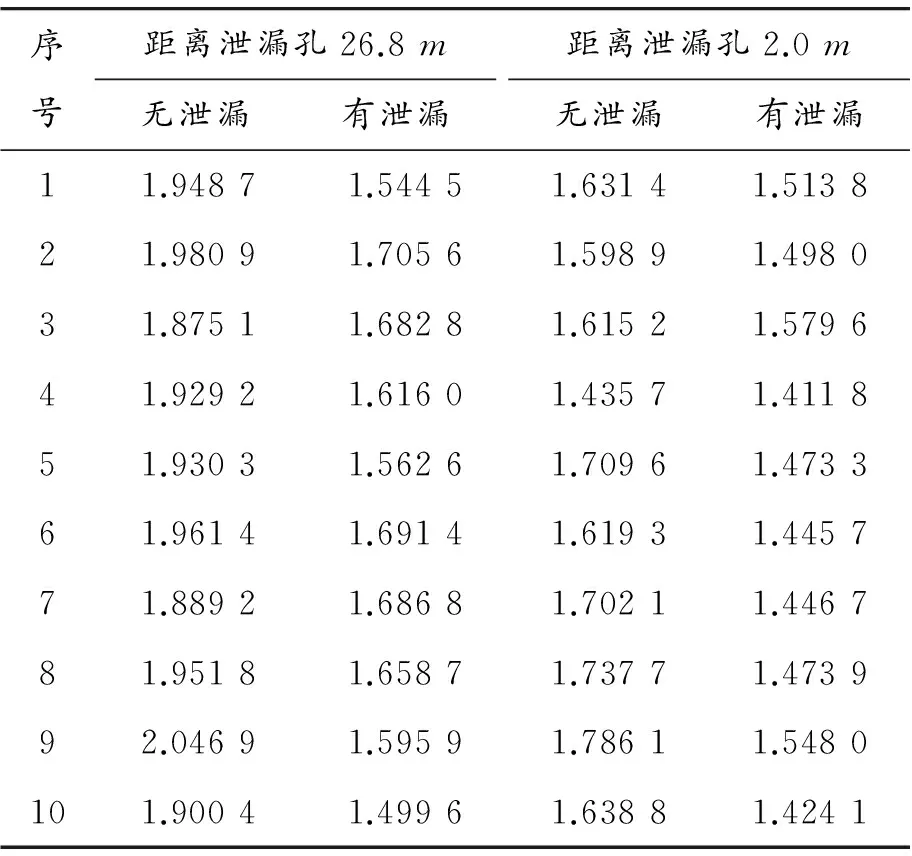
表1 不同距离下有泄漏和无泄漏奇异值熵对比

图3和图4表明：相对于无泄漏状态，管道泄漏声发射信号具有明显的冲击性，幅值更大。为使泄漏判断更加简洁和量化，运用本文提出的方法求取奇异值。从图5和图6中可以看出：泄漏状态下的奇异值均值大于非泄漏状态下的奇异值均值，与前述理论分析相符。从表1可以看出，管道泄漏状态下管道的声发射信号奇异值熵相对较小，非泄漏状态下奇异值熵相对较大，与仿真预测相符。综上所述，本文的方法可以较好地诊断出管道泄漏与非泄漏两种状态。

4 结束语

将内禀模态奇异值熵的概念引入到声发射管道泄漏检测中，提出了基于内禀模态奇异值熵的管道泄漏诊断方法。该方法将管壁声发射信号进行EMD分解得到内禀模态函数，进而求取信号的奇异值熵，通过对比奇异值熵的大小诊断管道有无泄漏。该方法简单易行、实用性强，但对计算机性能要求较高。

通过仿真对比两组信号奇异值熵的计算结果，可见计算结果与理论分析相符，表明基于内禀模态奇异值熵的管道泄漏诊断方法是有效的。

运用本文的方法，分别对距离泄漏孔2.0 m和26.8 m处有泄漏和无泄漏两种状态的声发射实验信号进行分析。实验结果表明，该方法可以准确诊断管道有无泄漏。

[1] 黄维和,郑洪龙,王婷.我国油气管道建设运行管理技术及发展展望[J].油气储运，2014，33(12):1259-1262.

[2] 王立坤,王洪超,熊敏,等.长距离输油管道泄漏监测技术分析及研究建议[J].油气储运，2014，33(11):1198-1201.

[3] LIOU J C.Leak detection by mass balance effective for Norman wells line[J].Oil and gas journal,1996,94(17):4-7.

[4] MACLEAN A,MORAN C,JOHNSTONE W,et al.Detection of hydrocarbon fuel spills using a distributed fibre optic sensor[J].Sensors and Actuators A:Physical,2003,109(1):60-67.

[5] 袁朝庆,刘燕,才英俊.利用光纤温度传感系统检测天然气管道泄漏 [J].天然气工业，2006，26(8):117-119.

[6] 付俊涛,李玉星,孟令雅,等.输气管道泄漏音波与干扰信号特征提取[J].石油化工高等学校学报，2012,25(2):1-8.

[7] MENG L Y,LI Y X,WANG W C,et al.Experimental study on leak detection and location for gas pipeline based on acoustic method[J].Journal of Loss Prevention in the Process Industries,2012,25(1):90-102.

[8] HUANG N E,SHEN Z,LONG S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London.Series A:Mathematical,Physical and Engineering Sciences,1998,454(1971):903-995.

[9] HUANG N E,ATTOH-OKINE N O.The Hilbert-Huang Transform in Engineering[M].USA:CRC Press,2005.

[10]傅祖芸.信息论[M].3版.北京:电子工业出版社,2013.

(责任编辑 杨文青)

Pipeline Leakage Detection Based on Singular Value Entropy of IMFs

YUAN Pei-long1, ZHOU Shao-qi1, ZHOU Ying-tao2, ZHANG Yi-fan2， TANG Hang1

(1.Department of Military Petroleum Supply Engineering, Logistical Engineering College,Chongqing 401331，China； 2.Unit 68101 PLA, Shaanxi, China)

Pipeline leakage diagnosis is the precondition of leakage location. A new method based on singular value entropy of Intrinsic Mode Functions (IMFs) is proposed aiming at the non-stationary characteristic of the acoustic emission (AE) signal from pipeline leakage for leakage detection. The IMFs is obtained by EMD from AE signal, and the initial feature vector is composed by IMFs. The singular value entropy of the vector is used for leakage detection. Simulation and experiments indicates the effectiveness of the proposed method.

intrinsic mode function; singular value entropy; pipeline leakage；acoustic emission

2016-06-22 基金项目：重庆市自然科学基金资助项目 (CSTC,BB0168)

袁培龙(1992—)，男，河南平顶山人，硕士研究生，主要从事油气储运工程缺陷检测技术方面研究，E-mail:yuanpeilong1992@163.com；通讯作者 周绍骑(1962—)，男，教授，主要从事油气储运控制技术与系统方面研究。

袁培龙，周绍骑，周颖涛，等.基于内禀模态奇异值熵的声发射管道泄漏诊断[J].重庆理工大学学报(自然科学)，2016(11):60-64.

format：YUAN Pei-long, ZHOU Shao-qi, ZHOU Ying-tao, et al.Pipeline Leakage Detection Based on Singular Value Entropy of IMFs[J].Journal of Chongqing University of Technology(Natural Science)，2016(11):60-64.

10.3969/j.issn.1674-8425(z).2016.11.011

TE973.6

A

1674-8425(2016)11-0060-05