铜官山矿田深部构造的三维计算模拟及其找矿意义

刘亮明, 曹　伟(中南大学 计算地球科学研究中心, 教育部 有色金属成矿预测重点实验室, 湖南 长沙 410083)

铜官山矿田深部构造的三维计算模拟及其找矿意义

刘亮明, 曹伟
(中南大学 计算地球科学研究中心, 教育部 有色金属成矿预测重点实验室, 湖南 长沙 410083)

计算模拟已成为研究矿田深部三维构造重要可行手段, 对深部找矿具有重要意义。基于铜官山矿田地质背景及所获勘查数据特征, 我们采用知识驱动下多级约束和多源数据融合建模方法模拟矿田范围内–2000 m 以上主要地质界面。以逆冲推覆导致断展–断弯褶皱理论模式解释大地测深的电阻率数据, 推断地质界面位置, 在 Micromine- GOCAD耦合平台上在多级约束下融合多源的界面位置数据, 以离散光滑插值算法和Delaunay三角网剖分法重构主要地质界面, 在计算机虚拟空间再现矿田三维构造格架。结果显示: 铜官山岩体和天鹅抱蛋岩体三维形态变化复杂, 总体上向西倾, 向深部岩体规模快速变小。位于铜官山岩体东接触带的铜官山铜矿田深部无找矿潜力, 原因是接触带产状变陡, 并且是岩体直接与上泥盆统砂岩接触; 矿田深部主要构造为走向NE并沿倾向弯曲的逆冲推覆断层; 铜官山背斜东翼含矿的中–上石炭统层位向深部倒转后又在–1200 m至–1500 m深度返转成向东南缓倾的正常层位, 其底部与逆冲推覆断层重合, 是深部找矿的有利靶区。

深部构造; 三维模型; 计算模拟; 铜官山矿田

0　引　言

随着浅部矿产资源日益减少, 深部找矿不仅成为找矿勘查重要增储方向, 也成为最具挑战性方向(翟裕生等, 2004; 刘亮明等, 2005; Williams, 2005; 刘亮明和蔡爱良, 2009)。任何矿床空间定位都与构造密切相关(陈国达, 1985)。深部构造的深度隐伏使得深部构造的探测和分析存在相当大难度, 深部构造研究实际也就成了深部找矿所面对主要挑战之一。

在大多数矿田中, 深部构造组成要素在三维空间内复杂多变, 传统地质方法显然难以充分揭示勘查区域内地质要素的特征及其时空规律, 这已成为制约成矿理论预测能力主要原因(刘亮明, 2007)。要依据并不充分信息, 在三维空间内尽可能准确表征深部构造和了解深部地质过程, 计算模拟已成为一种必不可少的有效方法(赵义来和刘亮明, 2011; Liu et al., 2012)。随着计算机技术、计算图形学和信息科学发展, 复杂地质体形态三维计算模拟在图形生成算法、建模方法、不确定性分析、信息融合以及勘查应用等方面都取得令人瞩目的发展(Lorensen and Cline, 1987; Mallet, 1989, 2002; Victor, 1993; Houlding, 1994; Gong et al., 2004; Xue et al., 2004; Wu et al., 2005; Turner, 2006; Frank et al., 2007; Bistacchi et al., 2008; Calcagno et al., 2008; Kaufmann and Martin, 2008; Caumon et al., 2009; Zanchi et al., 2009; Ming et al., 2010; Wellmann et al., 2010; Wellmann and Regenauer-Lieb, 2012; Bouza-Rodríguez et al., 2014; Elsheikh A H and Elsheikh M, 2014; Saalmann and Laine, 2014), 这些成果为三维计算模拟复杂的深部构造创造了有利条件。

铜官山矿田是安徽铜陵地区一个主要铜金多金属矿田, 矿田内主要矿床有铜官山铜矿、金口岭铜矿、天马山硫金矿和黄狮涝金矿。虽然这个矿田已经历长期开发(最早可追溯到唐代), 地表和浅部资源已消耗殆尽, 但近年来的深部找矿勘查工作显示深部可能还存在相当可观的隐伏矿体。由于铜官山矿田矿床类型主要是与岩体相关的矽卡岩型和层控矽卡岩型, 长期以来, 地质研究重点主要是矿床成因(郭文魁, 1957)、成矿岩体(周泰禧等, 1987; 杨学明和林文通, 1988; 杜杨松等, 2004, 2007; 吴才来等, 2010; 赵乘乘等, 2012)和矿床地球化学(田世洪等, 2005; 李红阳等, 2008; 杨秋荣等, 2010)。对于矿田构造研究并不深入, 主要集中于地表和浅部揭露构造的几何学及其与矿体空间关系方面(薛虎等, 1983;雷世和, 1985; 万仁虎, 2004)。对深部构造了解甚少,更没有涉及到深部三维构造格架, 这一局面无疑会严重制约深部矿体预测和勘查。本文综合集成有关铜官山矿田深部地质和地球物理信息, 以计算模拟方法再现矿田的深部三维构造格架, 并对深部找矿有利靶区进行预测分析。

1　地质背景

铜官山矿田位于铜陵矿集区最西部, 西邻长江。矿田最基本地质特征是在晚古生代以碳酸盐岩为主的沉积岩中侵入以闪长岩为主要成分的浅成侵入岩体, 区内所有矿床都与这些长英质浅成岩体密切相关。地表出露岩体主要有3个: ①铜官山岩体;②天鹅抱蛋岩体; ③金口岭岩体(图1)。铜官山岩体地表呈椭圆形, 出露面积为 1.5 km2, 岩性主要为石英闪长岩。锆石 SHRIMP U-Pb同位素年龄为141.8±1 Ma(吴才来等, 2010), 为燕山早期。天鹅抱蛋岩体地表呈不规则圆形, 面积约 0.8 km2, 岩性主要为闪长岩, 锆石 SHRIMP U-Pb同位素年龄为141.3±1.3 Ma(吴才来等, 2010)。金口岭岩体地表呈一长轴近南北不规则椭圆形, 出露面积约 5 km2。岩体矿物成分和化学成分与铜官山岩体相似, 主要为石英闪长岩, 其黑云母 Ar-Ar同位素年龄为 137 Ma(周泰禧等, 1987)。考虑到铜官山岩体也获得136 Ma的角闪石 Ar-Ar同位素年龄(周泰禧等, 1987),明显低于锆石 U-Pb同位素年龄。金口岭岩体与铜官山岩体、天鹅抱蛋岩体应同样为燕山早期岩浆活动产物。

围绕3个岩体出露地层为志留系‒三叠系(图1)。主要地层单元有: ①上志留统茅山组(S3m), 为砂岩、粉砂岩夹砂页岩; ②上泥盆统五通组(D3w), 主要为砂岩, 有少量砾岩; ③中–上石炭统(C2+3), 主要为白云岩、白云质灰岩和灰岩, 已变质成大理岩;④下二叠统栖霞组(P1q), 主要为生物碎屑灰岩, 已变质成大理岩; ⑤下二叠统孤峰组(P1g), 主要为硅质岩和硅质灰岩; ⑥上二叠统龙潭组(P2l), 为炭质页岩和粉砂页岩, 夹煤层; ⑦上二叠统大隆组(P2d),为硅质页岩和硅质灰岩; ⑧下三叠统殷坑组(T1y),主要为夹粉砂质页岩的灰岩; ⑨下三叠统和龙山组(T1h), 为含泥质条带灰岩; ⑩下三叠统南陵湖组(T1n), 为中厚层灰岩。

铜官山矿田地表主要构造为轴向 NE铜官山背斜, 其次为走向NE和NW断层(图1)。铜官山背斜为向北东倾伏的不对称倒转背斜, 背斜轴线整体方向为42°左右。以铜官山制高点为分界, 整个背斜构造分为两段, 北东段背斜转折端向北东方向倾伏,倾伏角近 10°, 形成较长倾伏端, 地表为第四系覆盖,下伏地层从五通组到殷坑组都有。其北西翼地层向北西方向倾, 倾角为30°～50°, 南东翼地层在浅部倾向东南, 倾角为 25°左右, 向深变陡, 并逐渐转为倾向北西。背斜西南段, 转折端向上拱, 呈穹湾状, 其核部地层为志留系砂页岩, 两翼地层从泥盆系到三叠系都有, 其北西翼地层向北西倾, 倾角为 40°～60°,其东南翼地层也向北西倾, 倾角大于60°。

铜官山矿田范围内已发现矿体主要为4种类型:①接触带矽卡岩型铜(铁、硫)矿体, 产于岩体与碳酸盐岩的接触带上, 成矿岩体主要为铜官山岩体, 其次为金口岭岩体; ②层控矽卡岩型(铁、硫)矿体, 矿体从岩体的接触带顺岩层延伸; ③层控硫金矿体,含矿层位主要为中–上石炭统碳酸盐岩; ④脉状铜(钼、金)矿体, 规模小, 主要产于靠近接触带的岩体和碳酸盐岩中。

矿田内已发现矿体空间分布及其与其他地质要素之间关系显示: 控制矿体空间位置与规模的两个主要地质因素是成矿岩体和中–上石炭统碳酸盐岩,所以通过深部构造研究揭示岩体在深部形态变化(包括是否存在未发现的隐伏岩体)以及中–上石炭统在深部的展布对预测和勘查深部矿体具有十分重要的意义。

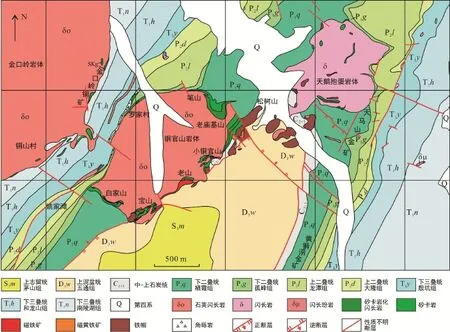
图1　铜官山矿田地质简图(据铜陵有色金属集团股份有限公司矿产资源中心, 2011修改)Fig.1　Geological sketch map of the Tongguanshan ore field

2　地质构造三维形态的计算模拟

2.1三维形态计算模拟方法

依据低维地质数据构建三维地质体模型计算模拟方法很多, 概括起来可分为 3类: ①面元模拟(surface-based modeling); ②体元模拟(volume-based modeling)和③混合模拟(hybrids modeling)(Shi, 1996; Gong et al., 2004; Bouza-Rodríguez et al., 2014)。面元模拟是根据地质体边界点和线构建地质体边界面,依生成面的方法不同模拟方法不同, 主要有: 不规则三角网(triangulated irregular network, 简称 TIN)模拟(De Floriani, 1989)、边界再现(boundary representation, 简称B-Rep)模拟(Stroud, 2006)、非均匀有理 B样条曲线(non-uniform rational B-splines,简称NURBS)模拟(Fisher and Wales, 1991)等。体元模拟是用各种形状体元来拟合地质体, 主要有体素(volumetric pixel, 简称 Voxel)模拟(Marschallinger, 1996)、八叉树(octree)模拟(Dunstan and Mill, 1989)、四面体格网(tetrahedron network, 简称 TEN)模拟(Pilout et al., 1994)、三棱柱(tri-prism, 简称TP)模拟(Houlding, 1994)等。混合模拟则将两种方法混合使用, 如Octree-TEN(李德仁和李清泉, 1997)、TIN-Octree (Shi, 1996)等。

由于地质要素中有不少是二维延展, 如地层界面、断层、不整合面等, 面元模拟在地质体三维模拟中有着比体元模拟更加明显优势(Houlding, 1994; Caumon et al., 2009)。TIN已成为构建三维地质模型最为广泛采用方法, 其基本原理是将空间上无重复的散乱数据点集按剖分规则进行三角剖分, 使这些散乱点形成连续但不重叠的不规则三角面片网, 并以此来描述三维物体的表面。TIN模拟中最广泛使用的剖分规则是Delaunay三角网规则, 这最早是由俄罗斯数学家 Delaunay(1934)提出并最终以他的名字命 名 的 剖 分 规 则 (Victor, 1993; George and Borouchaki, 1998), 它可以使剖分出的TIN最小内角最大化, 这就能最大限度地避免“瘦长”三角形, 从而自动向等边三角形靠近, 因此, Delaunay剖分被认为是最优的三角网剖分法之一。 Delaunay三角网最重要性质是空圆特性, 即三角网中任意一个三角形外接圆范围内必然不包含其他三角形顶点, 这条特性成为构建Delaunay三角网的首要准则和自动剖分算法的基础。基于Delaunay法则创造的一些算法已成三维形态模拟的精典算法, 如 Lawson算法、Bowyer-Watson算法(Rice and Usowt, 1968; Rebay, 1993; George and Borouchaki, 1998)。

由于空间数据不充分和不均匀分布, 直接由原始数据点经Delaunay三角剖分生成三维曲面偏离真实且极不美观(如图2a), 还必须进一步优化。优化途径有两条, 一是由一些插值的算法加密数据点; 二是人工插入一些关键控制点。通过插值加密数据点算法中以离散光插值(discrete smooth interpolation,简称DSI)算法应用最广, 同样数据经过DSI处理后的效果显然好很多(如图2b)。

DSI算法是Mallet (1989, 1992, 2002)发明的, 其基本内容是: 对一个离散化自然体构建其各个部分相互联系的网格(曲面)模型, 根据约束条件已知某些点位置或属性值, 则未知节点上的相应值可以通过解线性方程得到。设网格所有节点 k构成的集合为Ω, φ(k)为定义在Ω上的函数; 设对于Ω的子集L中节点l, φ(l)已知, 对于Ω的子集I中节点i, φ(i)未知; L+I=Ω。在Ω上, 对已知点{φ(l): l∈L}可以构建无穷多个插值函数 φ(k), 而离散光滑插值的目的即是从这些插值函数中找到一个使给定准则 R*(φ)有最小值的函数。R*(φ)的表达式为:

R*(φ)= R(φ)+ρ(φ)

其中, R(φ)为函数 φ(k)的全局粗糙度, ρ(φ)表征函数φ(k)与它应满足的约束条件之间的偏差值(约束违反度), 约束条件即为从原始数据提取的各种点状、线状约束。可见DSI插值生成的曲面需要满足拟合约束及光顺两个要求。即通过DSI插值能够在满足所有约束条件下使生成曲面尽可能地光顺美观,光顺美观曲面是否代表真实地质界面则取决于约束条件多少。由于矿田深部有工程控制的约束条件稀少, 所以人工插入控制点就显得尤为重要。人工插入控制点可靠性和效果取决于建模者对模拟对象真实形状了解。

基于铜官山矿田实际情况, 我们对矿田深部构造计算模拟采用基于Delaunay三角剖分的TIN面模拟法模拟矿田构造中主要地质界面, 对缺失数据一些关键点通过地质构造理论对电阻率数据的解释来决定人工插值, 最终由 DSI算法进行优化处理。采用计算模拟软件为 Micromine和 GOCAD。Micromine是由澳大利亚 Micromine公司开发专门进行矿床勘探和开发设计的商业软件(见 http: // www.micromine.com/), 在勘探数据录入和管理方面以及图形操作方面具独特优势。GOCAD是由法国Nancy大学开发用于地质对象三维建模的软件(见http: //www.gocad.org/), 由于软件采用DSI算法, 在生成面模型时具有独特优势。所以我们在建模时,采用 Micromine进行勘探数据录入和处理, 而用GOCAD来生成最终的面模型。

图2　DSI优化效果对比Fig.2　Efficiency of DSI optimization

2.2模拟数据及其所存在不足

铜官山矿田长期勘探和开发积累了大量地质勘探资料, 但由于几个矿山都经历过关破、转产或准备转产等, 不少资料已丢失。早期勘探钻孔和坑道测量、编录和分析数据基本都已丢失, 只能找到部分勘探线剖面图。目前可利用数据包括如下4种类型: ①早期勘探剖面和中段平面图, 不完整, 共计 77幅剖面图、46幅中段及地表图; ②近年来施工的地质探矿钻孔资料, 孔口坐标、测斜数据、编录数据和分析数据齐全, 共计447个钻孔, 99812 m岩性编录; ③包含部分老钻孔的新近完成钻孔勘探线剖面图, 共计26幅; ④我们新近完成的大地电磁测深电阻率数据, 共计441个测点的9475个电阻率数据, 探测深度到–2000 m。

上述看似庞大数据其实对建立如此大面积的矿田深部构造模型来说还是非常不充足的, 表现在:①由工程控制的地质数据分布范围太局限, 平面上限于矿体分布区, 深度上大都在–500 m以上, 超过1000 m钻孔只有5个, 超过500 m钻孔也只有50个;②深部的地质构造主要靠大地电磁测深获得的电阻率数据来推断。电阻率数据至少存在3个方面问题:第一、由于地表建筑和工农业设施, 很多地方无法进行大地电磁测深; 第二、地表和地下电力设施的干扰使得获得的电阻率数据不可避免地含有假异常;第三、依电阻率数据解释深部地质构造本身毫无疑问具有很强多解性。

正是由于模拟数据存在上述不足, 可以肯定将上述数据输入计算模拟软件平台不可能由计算机能自动生成一个合理的矿田构造格架的三维模型。计算模拟远非仅仅依靠计算机就能胜任工作, 还需要地质人员应用地质知识从理论上进行推断和选择,以弥补模拟数据不足。

2.3知识驱动多级约束和多源数据融合模拟途径

我们以面元模型模拟铜官山矿田的深部地质构造, 需要重构矿田范围内–2000 m深度以上的主要地质界面, 就是将工程控制的地质边界和推断的地质界面数据通过三维面模型形式在计算机虚拟空间中表达出来。由模拟流程来分析(图3), 模拟的最终结果可靠与否主要取决于输入的界面数据。由于工程控制范围十分有限, 大部分空间地质界面位置需要推断。推断的证据主要来自大地电磁测深所获得的电阻率数据, 所以由电阻率数据推断的深部地质界面对本区深部构造三维模拟至关重要。

图3　三维地质构造形态模拟流程图Fig.3　Flow chart for the 3D geological structural modeling

对于大地电磁测深获得电阻率数据, 通过Kriging插值获得了电阻率在三维空间分布的块体模型(图4)。这个模型非常形像地展示电阻率在三维空间分布, 总体上与铜官山背斜构造形态是吻合的,背斜核部未蚀变的志留系砂岩表现为高阻, 背斜翼部未蚀变的晚古生代碳酸盐岩也表现为高阻(图 4),但低阻却具有很强的多解性, 既可能是 P1q含炭质灰岩和P1l含煤页岩, 也能是蚀变的碳酸盐岩和砂岩或蚀变岩体, 还能是含水破碎带, 甚至还可能是因为干扰而引起。所以, 仅仅依靠这个电阻率三维空间分布模型无法正确推断无工程控制部位的地质边界。这就需要知识驱动, 即应用适合本地地质构造理论(概念)模式, 充分考虑地表及地下工程揭露地质体产状和空间形态变化趋势来解释电阻率分布三维块体模型, 推断地质界面的空间位置(图3)。地质构造理论模式是推断深部地质构造非常重要理论依据(刘亮明和蔡爱良, 2009), 而铜官山矿田需要推断地质界面空间范围要远远大于已有工程控制范围, 所以这种依构造理论模式推断深部地质构造的知识驱动作用对本区深部构造的计算模拟具有十分重要的意义。

图4　铜官山矿田电阻率三维分布块体模型Fig.4　3D block model of resistivity in the Tongguanshan ore field

以知识驱动推断地质(体)边界位置正确与否主要取决于所应用地质构造概念模式是否真正反映研究区地质构造形成的动力机制(刘亮明和蔡爱良, 2009)。在铜官山矿田, 地质构造概念模式必须从区域地壳演化的动力学解释形成铜官山背斜独特特征的机制和原因。综合分析铜官山背斜地质特征以及区域地壳动力学背景, 我们认为铜官山背斜是由逆冲推覆而派生的断展–断弯褶皱(图 5)。地层在冲断演化过程中, 推覆断层的滑动完全被褶皱作用所吸收, 没有滑动传递到褶皱以外, 形成断展褶皱(fault-propagation fold)。断层继续滑动可以追踪层间薄层带形成弯曲的推覆断层, 形成断弯褶皱(fault bend fold)。Suppe (1983)、Suppe and Medwedeff (1990)和Mercier et al. (1997)等创立的这种断展–断弯褶皱理论模式适用于铜官山矿田, 其证据有如下 3个方面: ①铜官山背斜是东南翼局部倒转的不对称背斜,而且这种不对称褶皱是铜陵–安庆地区褶皱的普遍特征, 这也是逆冲推覆形成褶皱的典型特征; ②铜陵–安庆地区褶皱的古生代地层中存在多个层间滑脱带, 如: D3w与C2+3之间、P2l和T1h之间; ③逆冲推覆是整个铜陵–安庆地区印支期造山的主要构造型式(董树文和邱瑞龙, 1993)。基于上述考虑, 我们将应用逆冲推覆引起断展–断弯褶皱理论模式来解释铜官山矿田大地电磁测深所获得的电阻率数据,推断矿田深部的主要地质界面。

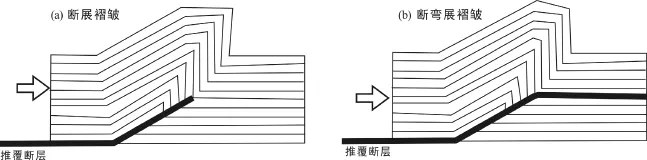
图5　逆冲推覆断层派生断展褶皱和断弯褶皱概念模式(据Suppe, 1983; Mercier et al., 1997修改)Fig.5　Conceptual model for thrust induced fault-propagation fold and fault-bend fold

将推断地质界面数据和控制地质界面数据输入到一个由Micromine和GOCAD相互耦合的计算平台, 采用知识驱动下多级约束和多源数据融合方法进行三维地质界面模拟, 基本流程见图3。整个模拟过程关键操作是人工插入控制点, 多级约束和多源数据融合是为了保证人工插入控制点的合理性和可靠性, 主要内容和操作包括如下4个方面。

(1) 用来保证插入点合理性和可靠性约束条件是多级的, 包括: ①来自工程点位置严格约束, 即插入点必须严格地与工程控制点相协调; ②来自地质现象的产状和形态变化趋势的约束, 即插入点必须符合这种产状和形态变化趋势; ③来自概念模式轮廓约束, 即插入点与已有控制点的空间展布应该与概念模式所反映的轮廓相吻合; ④来自三维电阻率场的块段约束, 即插入点与已有点所包围块体属性应该与电阻率场所反映属性一致。所有插入边界点要与这4级约束相符, 且同一属性插入点和控制点分布要大致均匀。

(2) 用于确定边界点位置和属性的数据是多源的, 包括: ①钻孔和坑道编录确定的边界数据; ②地表地质图确定的边界数据; ③勘探线剖面图和中段平面地质图圈定的边界数据; ④电阻率数据以及根据电阻率推断的边界数据。这些不同来源数据形式和可靠程度都不一样。将上述各类数据按照Micromine的点(位置, 属性)格式统一于同一坐标空间内进行编辑和操作。根据原始数据约束条件差异, 可将整个模拟区域分成多个子区域, 在各个子区域中通过控制点、解译线与辅助面混合使用, 插入尽可能合理边界点, 然后再将各子区域融合成一个统一的点数据库。

(3) 将所有点数据按 GOCAD格式要求导入GOCAD进行DSI处理, 然后再由Delaunay算法生成相应的曲面。

(4) 在整个模拟过程中, 知识驱动主要体现在两个方面: ①根据电阻率变化推断地质解释的选择,由于电阻率数据的地质解释具有多解性, 根据概念模式来选择一种合理解释; ②松散约束条件下多种可能模型选择。由于矿田深部严格工程约束稀少, 主要是来自概念模式和三维电阻率场的松散约束, 可能构建多种可选模型, 最后只能根据构造动力学背景知识和已清楚的矿田构造特征选择一个合理模型。

3　矿田构造三维模拟结果及找矿意义分析

应用上述计算模拟方法, 我们最终模拟铜官山矿田地表至–2000 m范围的下列地质界面: ①铜官山岩体的边界面; ②天鹅抱蛋岩体边界面; ③金口岭岩体的东部边界面; ④D3w与C2+3分界面; ⑤P1q与 P1g分界面; ⑥天马山矿床主要矿体的边界面;⑦铜官山矿床主要矿体的边界面; ⑧深部逆冲推覆断层, 模拟结果见图6。

综合分析地质构造三维计算模拟结果(图 6)和电阻率分布三维计算模拟结果(图4), 揭示铜官山矿田构造在深部空间展布具有如下规律, 这些规律对指示深部找矿具有重要意义。

(1) 铜官山岩体和天鹅抱蛋岩体作为铜官山矿田两个最主要控矿因素, 其空间形态变化复杂, 总体特征是位于铜官山背斜西北翼靠核部, 向西倾,并且向深部快速变小, 在–2000 m深度以上没有与这两个小岩株相连的岩浆房。

(2) 铜官山矿田最主要已有矿床是与铜官山岩体相关的铜官山铜矿床以及与天鹅抱蛋岩体相关的天马山硫金矿床。两个矿床的控矿构造及空间变化差异很大, 铜官山铜矿床矿体连续性较好, 主要受控于围岩岩性和接触带形态, 浅部接触带平缓, 围岩为中–上石炭统碳酸盐岩, 成矿好。向深部, 接触带变陡, 而且岩体直接与泥盆系砂岩接触, 成矿条件差, 所以铜官山岩体东接触带深部应该没有找矿潜力。天马山矿床矿体主要位于与天鹅抱蛋岩体相接触的中–上石炭统中, 矿体规模小, 连续性差, 矿体主要受控于层位, 而不是岩体的接触带, 矿体定位空间与D3w-C2+3分界面形态密切相关, D3w-C2+3分界面呈现出一系列沿倾向延伸的凹槽和凸起, 矿体趋向定位于凹槽靠凸起的部位, 向深部至–1200 m到–1500 m仍具成矿条件, 具有找矿潜力。

(3) 铜官山背斜东南翼地层在深部向北西倒转,但在–1200 m到–1500 m深度, 倒转地层又会返转成向东南缓倾的正常产状, 返转部位是北高南低, 意味着本区最有利成矿的中–上石炭统和下二叠统栖霞组在天马山矿床以东呈现向东南缓倾的产状, 位于–1200 m到–1500 m的深度。

(4) 深部最主要构造是弯曲的逆冲推覆断层,这个断层向北西陡倾部分切穿地层, 而东南缓倾部分则平行于地层, 而且是追踪D3w与C2+3的分界面。沿此断层陡倾部分是岩体侵位的有利场所, 电阻率三维分布模型也显示这一构造部位可能存在隐伏岩体。所以, 在矿田东部深部缓倾的 C2+3和P1q应该是找矿有利靶区。

4　结　论

基于铜官山矿田勘探资料及大地电磁测深电阻率数据, 采用知识驱动下多级约束和多源数据融合方法模拟矿田范围在–2000 m 以上主要地质界面,形象地展示矿田深部三维构造格架。结果显示: 铜官山岩体和天鹅抱蛋岩体形态变化复杂, 总体上向西倾, 向深部岩体规模快速变小。位于铜官山岩体东接触带的铜官山铜矿深部找矿潜力小, 原因是接触带产状变陡, 并且围岩也变成上泥盆统砂岩; 矿田深部最主要构造为走向 NE并沿倾向弯曲的逆冲推覆断层, 断层东南段向东南缓倾; 铜官山背斜东翼含矿层位中–上石炭统向深部倒转后又在–1200 m至–1500 m深度返转成向东南缓倾的正常层位, 其底部与深部逆冲推覆断层重合, 是深部找矿有利靶区。

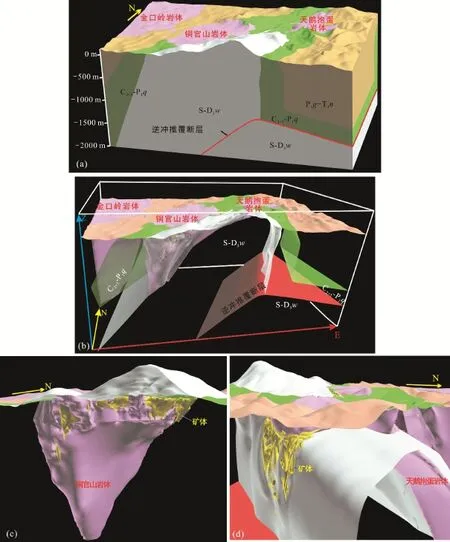
图6　矿田构造三维模型Fig.6　3D model of the geological structures in the ore field

致谢: 研究工作得到了国家自然科学基金和铜陵有色金属集团股份有限公司的资助, 铜陵有色金属集股份有限公司还对现场研究工作给予了大力支持,席振铢和范福来等承担了大地电磁测深工作, 在此深表感谢！感谢审稿人合肥工业大学袁峰教授和中国地质大学(武汉)左仁广教授所提的修改意见！

陈国达. 1985. 成矿构造研究法(第二版). 北京: 地质出版社: 1–4.

董树文, 邱瑞龙. 1993. 安庆–月山地区构造作用与岩浆活动. 北京: 地质出版社: 1–58.

杜杨松, 李顺庭, 曹毅, 秦新龙, 楼亚儿. 2007. 安徽铜陵铜官山矿区中生代侵入岩的形成过程: 岩浆底侵、同化混染和分离结晶. 现代地质, 21(1): 71–77.

杜杨松, 秦新龙, 田世洪. 2004. 安徽铜陵铜官山矿区中生代岩浆–热液过程: 来自岩石包体及其寄主岩的计据. 岩石学报, 20(2): 339–350.

郭文魁. 1957. 论安徽铜官山铜矿成因. 地质学报, 37(3): 317–323.

雷世和. 1985. 铜官山铜矿主控矿断裂构造的特征及找矿意义. 河北地质学院学报, 30(2): 10–21.

李德仁, 李清泉. 1997. 一种三维 GIS 混合数据结构研究. 测绘学报, 26(2): 128–133.

李红阳, 李英杰, 康桂玲, 曹积飞, 杨竹森, 侯增谦, 蒙义峰. 2008. 安徽铜官山铜–铁–金–硫矿床的地球化学特征. 地质科学, 43(2): 370–376.

刘亮明. 2007. 成矿理论的预测能力及其改善途径. 地学前缘, 14(5): 82–91.

刘亮明, 蔡爱良. 2009. 深部找矿: 地质理论、勘查技术、投资决策的难题及对策. 地质通报, 28(7): 923–932.

刘亮明, 吕俊武, 彭省临, 王国平, 方维萱, 邵拥军. 2005.成熟勘探区新一轮找矿: 勘查战略创新及铜陵矿集区找矿实例. 地质论评, 51(3): 325–333.

田世洪, 丁悌平, 侯增谦, 杨竹森, 谢玉玲, 王彦斌, 王训诚. 2005. 安徽铜陵小铜官山铜矿床稀土元素和稳定同位素地球化学研究. 中国地质, 32(4): 604–613.

铜陵有色金属集团股份有限公司矿产资源中心. 2011. 安徽省铜陵市铜官山矿区地形地质图(1: 5000).

万仁虎. 2004. 铜官山矿田金矿床类型和构造控矿作用分析. 地质力学学报, 10(2): 122–128.

吴才来, 高前明, 国和平, 郭祥炎, 刘良根, 郜源红, 雷敏, 秦海鹏, 陈其. 2010. 铜陵地区铜官山矿田侵入岩锆石SHRIMP定年. 地质学报, 84(12): 1746–1758.

薛虎, 车树政, 董茂兴, 张富陶. 1983. 安徽铜官山–马山金属矿田的构造研究. 中国地质科学院南京地质矿产研究所所刊, 4(3): 1–24.

杨秋荣, 王金芳, 冯景志, 侯增谦, 杨竹森, 蒙义峰, 王聪颖, 陈文韬. 2010. 安徽铜陵天马山金硫矿床地质地球化学特征. 地球学报, 31(2): 203–208.

杨学明, 林文通. 1988. 铜官山火成杂岩体成岩机理研究.地质论评, 34(1): 25–35.

翟裕生, 邓军, 王建平, 彭润民, 刘家军, 杨立强. 2004.深部找矿研究问题. 矿床地质, 23(2): 142–149.

赵乘乘, 杨晓勇, 冯敏, 孙卫东, 洪长春, 孙健, 胡俊杰,唐树平. 2012. 铜官山岩体矿物学–矿物化学特征:岩浆结晶动力学意义. 地质学报, 86(11): 1748–1760.

赵义来, 刘亮明. 2011. 复杂形态岩体接触带成矿耦合动力学三维数值模拟: 以安庆铜矿为例. 大地构造与成矿学, 35(1): 128–136.

周泰禧, 李学明, 赵俊深, 张富陶. 1987. 安徽铜陵铜官山矿田火成岩的同位素地质年龄. 中国科学技术大学学报, 17(3): 403–407.

Bistacchi A, Massironi M, Dal Piaz G, Dal Piaz G, Monopoli B, Schiavo A and Toffolon G. 2008. 3D fold and fault reconstruction with an uncertainty model: An example from an Alpine tunnel case study. Computers and Geosciences, 34(4): 351–372.

Bouza-Rodríguez B, Comesaña-Campos A, Menéndez-Díaz A and Garcia-Cortes S. 2014. A novel geometric approach for 3-D geological modelling. Bulletin of Engineering Geology and the Environment, 73(2): 551–567.

Calcagno P, Chilès J P, Courrioux G and Guillen A. 2008. Geological modelling from field data and geological knowledge Part I: Modelling method coupling 3D potential-field interpolation and geological rules. Physics of the Earth and Planetary Interiors, 171(1): 147–157.

Caumon G, Collon-Drouaillet P, Le Carlier, de Veslud C, Viseur S and Sausse J. 2009. Surface-based 3D modeling of geological structures. Mathematical Geosciences, 41(8): 927–945.

De Floriani L. 1989. A pyramidal data structure for trianglebased surface description. IEEE Computer Graphics and Application, 8(2): 67–78.

Delaunay B. 1934. Sur la sphere vide. Izv. Akad. Nauk SSSR, Otdelenie Matematicheskii Estestvennyka Nauk, 7: 793–800.

Dunstan S P and Mill A J B. 1989. Spatial indexing of geological models using linear Octrees. Computers and Geosciences, 15(8): 1291–1301.

Elsheikh A H and Elsheikh M. 2014. A reliable triangular mesh intersection algorithm and its application in geological modelling. Engineering with Computers, 30(1): 143–157.

Fisher T R and Wales R Q. 1991. Three-dimensional solid modeling of geological objects using non-uniformrational B-splines (NURBS) // Turner A K. Three dimensional modelling with geoscientific information systems. Dordrecht: Kluwer: 85–105.

Frank T, Tertois A L and Mallet J L. 2007. 3D-reconstruction of complex geological interfaces from irregularly distributed and noisy point data. Computers and Geosciences, 33(7): 932–943.

George P L and Borouchaki H. 1998. Delaunay Triangulation and Meshing: Application to Finite Elements. Paris: Hermes: 1–410.

Gong J, Cheng P and Wang Y. 2004. Three-dimensional modeling and application in geological exploration engineering. Computers and Geosciences, 30(4): 391–404.

Houlding S W. 1994. 3D Geoscience Modeling: Computer Techniques for Geological Characterization. Berlin: Springer: 1–301.

Kaufmann O and Martin T. 2008. 3D geological modelling from boreholes, cross-sections and geological maps, application over former natural gas storages in coal mines. Computers and Geosciences, 34(3): 278–290.

Liu L M, Zhao Y L and Sun T. 2012. 3D computational shape-and cooling process-modeling of magmatic intrusion and its implication for genesis and exploration of intrusion-related ore deposits: An example from the Yueshan intrusion in Anqing, China. Tectonophysics, 526–529: 110–123.

Lorensen W E and Cline H E. 1987. Marching cube: A high resolution 3d surface construction algorithm. Computer Graphics, 21(4): 163–169.

Mallet J L. 1989. Discrete smooth interpolation. ACM Transactions on Graphics, 8(2): 121–144.

Mallet J L. 1992. Discrete smooth interpolation in geometric modelling. Computer-aided design, 24(4): 178–191.

Mallet J L. 2002. Geomodeling. Oxford: Oxford Press: 1–600.

Marschallinger R. 1996. A voxel visualization and analysis system based on Autocad. Computer and Geosciences, 22(4): 379–386.

Mercier E, Outtani F and Lamotte D F D. 1997. Later-stage evolution of fault-propagation folds: Principles and example. Journal of Structural Geology, 19(2): 185–193.

Ming J, Pan M, Qu H and Ge Z. 2010. GSIS: A 3D geological multi-body modeling system from netty cross-sections with topology. Computers and Geosciences, 36(6): 756–767.

Pilout M, Tempfli K and Molenaar M. 1994. A tetrahedron-based on 3D vector data model for geoinformation // Molenaar M, de Hoop S. Advanced Geographic Data Modeling, Publications on Geodesy Vol. 40. Delft: Netherlands Geodetic Commission: 129–140.

Rebay S. 1993. Efficient unstructured mesh generation by means of Delaunay triangulation and Bowyer-Waston algorithm. Journal of Computational Physics, 106(1): 125–138.

Rice J R and Usowt K H. 1968. The Lawson algorithm and extensions. Mathematics of Computation, 22(101): 118–127.

Saalmann K and Laine E L. 2014. Structure of the Outokumpu ore district and ophiolite-hosted Cu-Co-Zn-Ni-Ag-Au sulfide deposits revealed from 3D modeling and 2D high-resolution seismic reflection data. Ore Geology Reviews, 62: 156–180.

Shi W Z. 1996. A hybrid model for 3D GIS. Geoinformatics, 1: 400–409.

Stroud I. 2006. Boundary representation modelling techniques. Berlin: Springer: 1–808.

Suppe J. 1983. Geometry and kinematics of fault-bend folding. American Journal of Science, 283(7): 684–721.

Suppe J and Medwedeff D A. 1990. Geometry and kinematics of fault-propagation folding. Eclogae Geologicae Helvetiate, 83(3): 409–459.

Turner A K. 2006. Challenges and trends for geological modelling and visualisation. Bulletin of Engineering Geology and the Environment, 65(2): 109–127.

Victor J D. 1993. Delaunay triangulation in TIN creation: An overview and a linear-time algorithm. International Journal of Geographical Information Systems, 7(6): 501–524.

Wellmann J F, Horowitz F G, Schill E and Regenauer-Lieb K. 2010. Towards incorporating uncertainty of structural data in 3D geological inversion. Tectonophysics, 490(3): 141–151.

Wellmann J F and Regenauer-Lieb K. 2012. Uncertainties have a meaning: Information entropy as a quality measure for 3-D geological models. Tectonophysics, 526–529: 207–216.

Williams N. 2005. Australian mineral exploration in the 21st century: Are we up to the challenge? Perth: Presentation at AMEC National Mining Congress.

Wu Q, Xu H and Zou X. 2005. An effective method for 3Dgeological modeling with multi-source data integration. Computers and Geosciences, 31(1): 35–43.

Xue Y, Sun M and Ma A. 2004. On the reconstruction of three-dimensional complex geological objects using Delaunay triangulation. Future Generation Computer System, 20(7): 1227–1234.

Zanchi A, Francesca S, Stefano Z, Simone S and Graziano G. 2009. 3D reconstruction of complex geological bodies: Examples from the Alps. Computers and Geosciences, 35(1): 49–69.

Computational 3D Modeling on Deep Structure Architecture and Implication for Ore Exploration in the Tongguanshan Ore Field, Tongling, China

LIU Liangming and CAO Wei
(Computational Geosciences Research Center, MOE Key Laboratory of Nonferrous Metallogenic Prediction, Central South University, Changsha 410083, Hunan, China)

Computational modeling has become an important virtual technique for revealing the deep structures in 3D, which is critical for deep ore exploration. In view of the geological setting and the exploration data available for the Tongguanshan ore field, we simulate the major geological interfaces within the ore field deep to −2000 m by applying the knowledge-driven modeling method, during which multi-sourced data are integrated under multi-scaled constraints. The concept model for thrust induced fault-propagation fold and fault-bend fold is used to interpret the MT resistivity data, and the inferred positions of geological interfaces are used where no drills or tunnels are available. The multi-sourced data about the geological interfaces are integrated under multi-scaled constraints in the soft platform of coupled Micromine and GOCAD. The algorithms of DSI and Delaunay TIN are applied to reconstruct the major geological interfaces for virtually revealing the structure architecture of the ore field. The final modeling results demonstrate that the Tongguanshan and Tian’ebaodan intrusions, with very complex spatial variation in 3D geometric shape, are generally west-dipping and diminished sharply at depth. The majority of the ore bodies of the Tongguanshan deposit occur in the shallow part of the east contact zone of the intrusion, however, the economic potential of ore mineralization at depth is permissive because the steeper and directly contact with the Upper Devonian sandstone. The principal structure deep in the ore field is the NE-trending bend thrust fault. The ore-hosting strata, the Mid- to Upper Carboniferous sequences, in the southeastern limb of the Tongguanshan upturn anticline will be appear as gently dipping strata and cut by the bend thrust fault at the depth of −1200 m to −1500 m, and thus is likely favorable target for ore prospecting.

deep structure; 3D model; computational modeling; Tongguanshan ore field

P542

A

1001-1552(2016)05-0928-011

10.16539/j.ddgzyckx.2016.05.003

2015-03-05; 改回日期: 2015-04-01

项目资助: 国家自然科学基金项目(41240017和41372338)资助。

刘亮明(1964–), 男, 教授, 主要从事矿床地质和构造地质研究。Email: lmliu@csu.edu.cn