漂浮式立轴潮流水轮机波浪载荷分析
盛其虎,李 超,张学伟,孙 科,荆丰梅,马 勇
(1.哈尔滨工程大学 海洋技术研究所,黑龙江 哈尔滨 150001;2.国家海洋技术中心,天津 300112)
漂浮式立轴潮流水轮机波浪载荷分析
盛其虎1,李超2,张学伟1,孙科1,荆丰梅1,马勇1
(1.哈尔滨工程大学海洋技术研究所,黑龙江哈尔滨150001;2.国家海洋技术中心,天津 300112)
波浪对漂浮式潮流能水轮机的水动力性能具有重要的影响,论文采用切片理论建立和三维水轮机无辐射运动时立轴潮流水轮机水动力载荷近似计算公式,计算分析了浪流同向条件下,海能1号2×150 kW漂浮式潮流电站两叶片固定偏角立轴水轮机在波浪中的水动力载荷。计算结果表明,波浪中潮流水轮机水动力具有双频特性;水轮机工作工况下,每增加1 m波高,水轮机极限载荷增加27%,在相同波高条件下,主轴极限载荷随波长的增加而增大。
潮流能;立轴水轮机;漂浮式潮流电站;水动力;波浪载荷
浮式潮流电站具有检修维护方便,单机安装成本低的优点,非常适合进行潮流能开发利用。浮式潮流电站的水轮机浮于水面附近,潮流流速和波浪情况都会对水轮机的水动力载荷产生影响。Barltrop[1]对直径为0.4 m的三叶片水平轴水轮机进行了波浪实验,测试了不同波高及不同波浪频率下的叶轮推力和力矩。与无波浪时相比,水轮机在波浪中的载荷均值基本上保持不变,但是叶轮力矩和推力波动随着波高逐渐增大。同时,运用动量叶素理论,结合线性自由波条件对水轮机水动力进行了计算,计算值与实验值相比吻合较好。Galloway、Myersh和Bahaj等人[2]研究波浪对水轮机水动力性能的影响,针对一个直径0.8 m的三叶片水平轴水轮机进行了水池实验,来流速度为1.5 m/s,波高0.08 m、波浪周期1.34 s,与来流方向同向。实验发现有波浪情况下叶轮转矩和推力的平均值基本上不变,而推力波动最大增加37%、力矩波动最大增加35%。Luznik[3]等对直径为0.46 m的三叶片水平轴水轮机进行了波浪实验,与前面的试验相同,叶轮的平均性能并没有发生影响,而波动现象特别明显,叶轮能量系数波动增加70%。2013年Lust Ethan E[4]等人进行了同样的试验,结论相近,同时运用动量叶素理论与波浪理论结合的方式进行了理论计算。Hu Zhen[5]分析了流速周期变化引起的叶片载荷波动对叶片疲劳性能的影响。2012年,Faudot Céline[6]结合动量叶素理论与波浪理论对水轮机水动力进行计算,同时考虑了附加质量对叶片受力的影响,但该方法没有考虑动态失速的影响和水轮机的非定常效应。2015年盛其虎、周念福等[7]针对固定叶片二维立轴旋转叶轮在均匀流且轴系做强迫简谐振动时的水动力特性进行了CFD数值模拟,并对水轮机水动力极值的包络线进行了研究,发现叶轮轴系振荡时,水动力极值的包络线周期与轴振荡频率一致,且包络线的振幅和轴振荡速度幅值成线性关系,并且在轴简谐振荡时,包络线非常接近正弦曲线。2016年,盛其虎、荆丰梅[8]等人研究了二维立轴叶轮纵荡情况下的水动力导数,并给出了二维叶轮纵荡水动力和叶轮工况的变化关系。以上研究表明无不表明波浪对水轮机水动力的重要影响。
本文采用切片理论建立了三维立轴潮流水轮机工作状态时波浪激励力的计算模型,计算了浪流同向时立轴叶轮的波浪激励力。
1 数学模型
立轴叶轮的水动力载荷F可写成载荷系数的形式:
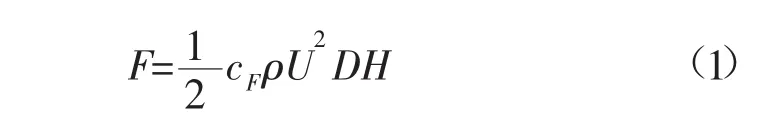
式中:cF为载荷系数;ρ为海水密度;U为潮流流速;D为叶轮直径;H为叶轮高度。考虑到波浪的影响,这里的水动力载荷cF为时间的函数。文献[8]给出的二维立轴潮流水轮机水动力载荷纵荡水动力载荷系数的解耦形式:
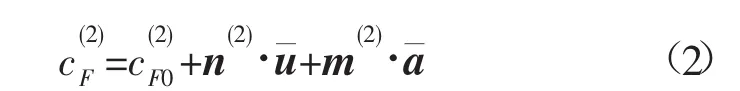
各项系数的分量可表示为以下形式:
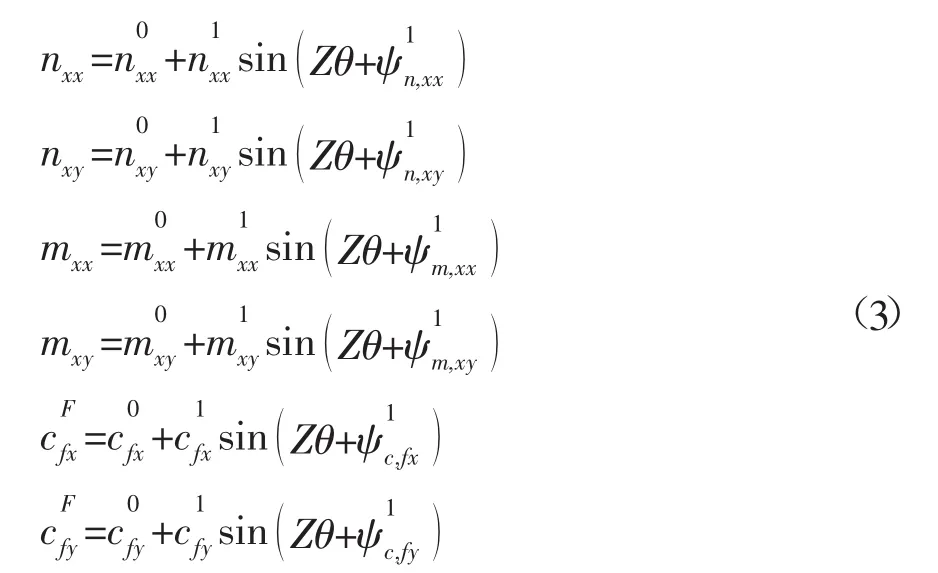
由于直叶片立轴水轮机不同高度处截面形状相同,而且轴向流动对水轮机水动力影响较小,根据切片理论,在不考虑两端三位效应的前提下,三维水轮机的流载荷可通过不同截面处二维水轮机流载荷的叠加得到。对于浸深为h0三维立轴潮流水轮机,当不考虑潮流速度梯度时,不同深度处水轮机的平均流速U和速比是一致的;若不考虑水轮机辐射运动,水轮机的相对速度波动为波浪引起的水质点水平运动速度,该速度随水深增加而衰减。
对于有限水深平面行进波,若波高为a,波浪圆频率为ω,水深为h,波数为k,则行进波速度势为:
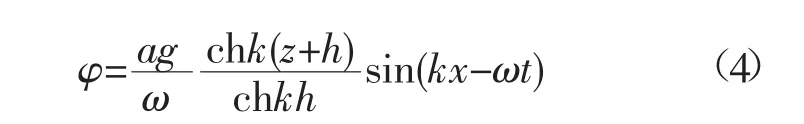
式中:圆频率ω满足色散关系ω2=gkthkh。考虑到水流速度的影响,叶轮主轴位置处的波浪水质点水平运动速度为:
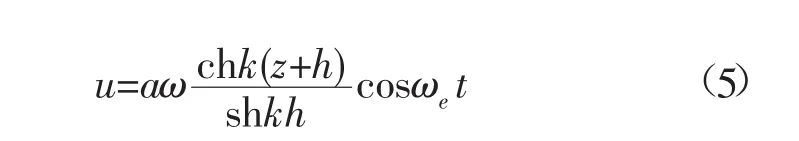
式中:ωe=kUcosx+ω为遭遇频率;x为浪向角。对于三维立轴潮流水轮机,当潮流流速和旋转角速度不变时,忽略附加质量力的影响,波浪中潮流能水轮机的水动力载荷系数为:
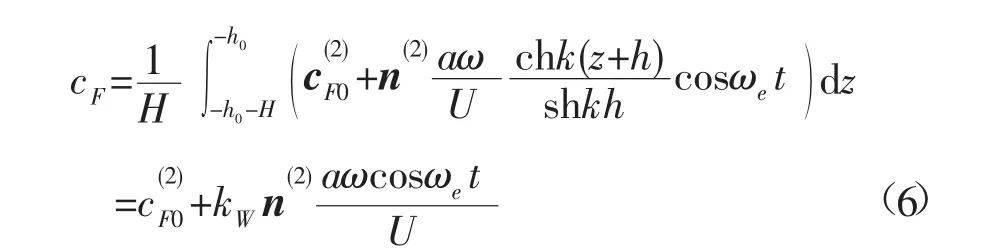
其中单位波幅水轮机波浪激励力:
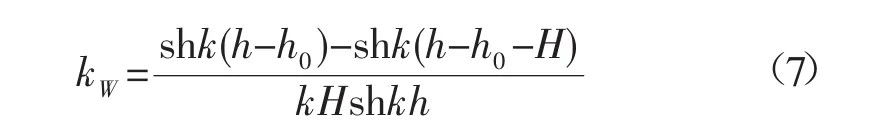
以自由面为原点,水轮机的水动力纵倾力矩:
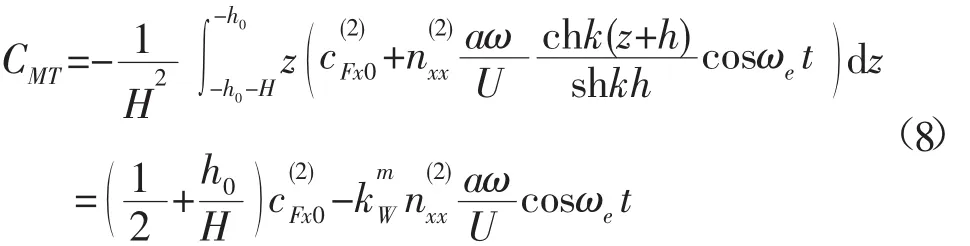
水动力横倾力矩:
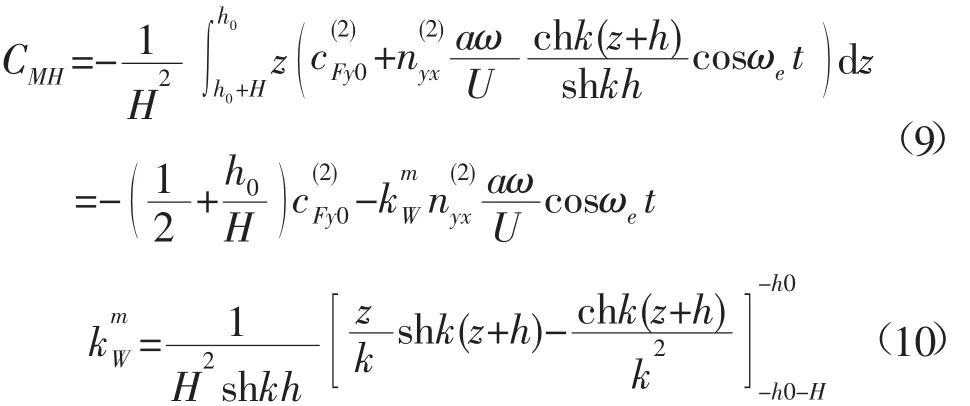
从式(6)~式(10)可以看出,立轴水轮机的波浪激励力和激励力矩和波幅成线性关系。
2 数值结果
以2×150 kW漂浮式立轴潮流电站的2叶片固定偏角水轮机为例,水轮机直径4 m,高度5.5 m,弦长1.2 m,水轮机浸深0.5 m,电站所在位置水深30 m。取波高2 m,波长50 m,根据文献[8]给出的二维叶轮水动力系数,按照式(4)~式(10)可以计算浪流同向时各个时刻水轮机主轴的水动力载荷和力矩。图1为水轮机在无波浪时的主轴载荷,图2为该工况时叶轮主轴的流载荷,其中Fx为流向载荷,Fy为侧向载荷;图3为水轮机主轴的水动力力矩,其中MT为研流向弯矩(纵倾力矩),MH为侧向弯矩(横倾力矩)。
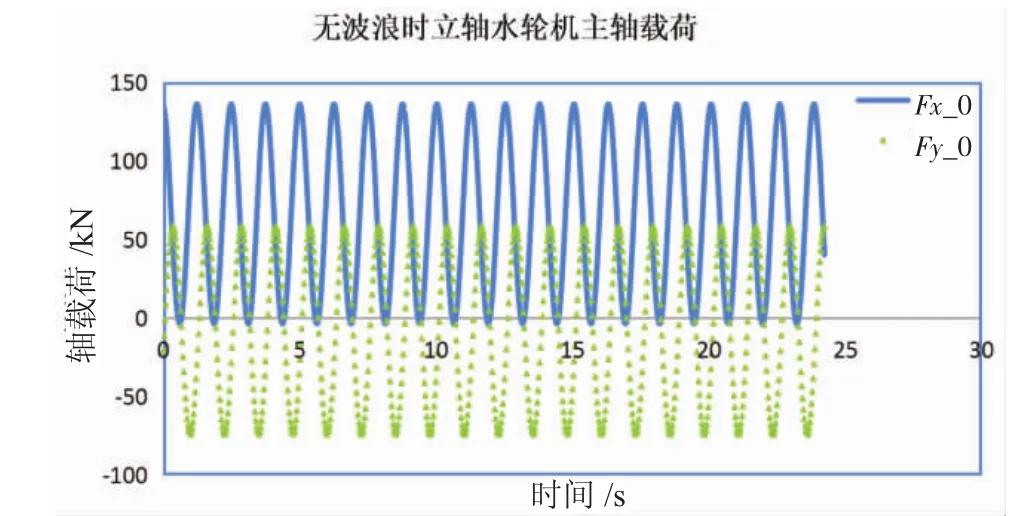
图1 均匀流中水轮机轴载荷(无波浪)
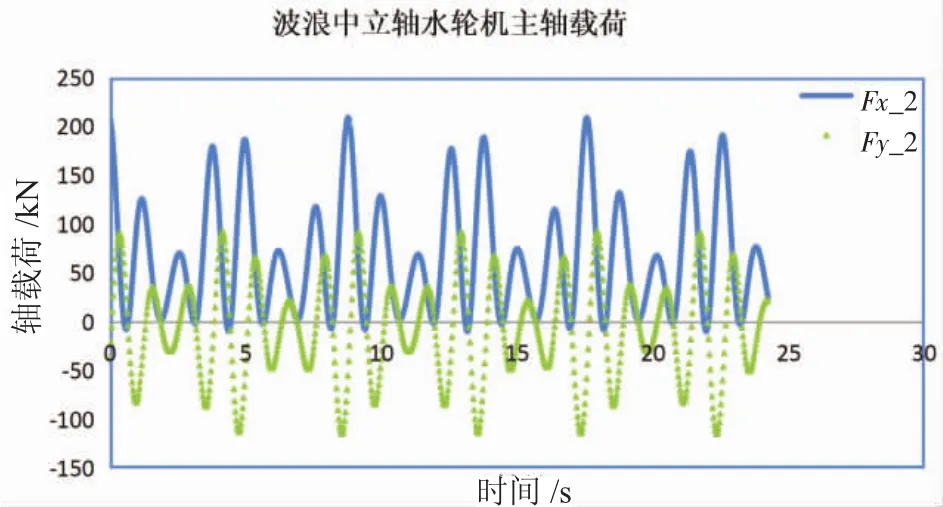
图2 50 m波长,2 m波高时立轴水轮主轴水动力载荷
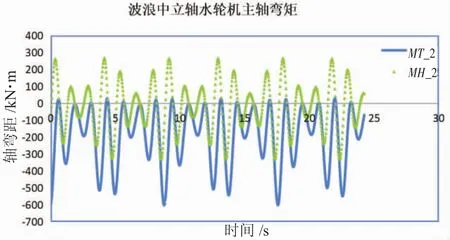
图3 50 m波长,2 m波高时立轴水轮主轴水动弯矩
从计算结果来看,无波浪时,水轮机主轴载荷的极值基本保持一致,有波浪时,水轮机的载荷极值随时间改变,但是极值的包络线具有周期变化规律,载荷变化规律呈现双频特性。同时由于波浪的影响,水轮机载荷的最大值增大。以流向载荷为例,2 m波高时,水轮机最大流向载荷增加了54%,纵倾力矩增加55%。按照波浪载荷与波幅成线性关系的规律,波高每增加1 m,该水轮机的流载荷增加27%。当波高为4m时,水轮机的流载荷增大1倍。
图4给出了主轴流载荷极值随波长的变化关系,尽管随着波长的增加,波浪的圆频率减小,水质点水平运动速度降低,但是由于长波随水深的衰减速度减小,随着波长的增加,波浪对主轴极限载荷的增幅增大。
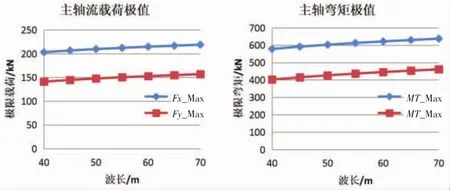
图4 主轴水动力载荷极值随波长的变化关系
3 结论
本文基于切面理论建立了三维立轴水轮机无辐射运动时主轴载荷的计算模型,借助文献[8]的二维水轮机计算结果,给出了2×150 kW的2叶片水轮机在波浪中的主轴载荷变化规律,计算结果表明,波浪条件下水轮机的水动力载荷具有双频变换特征;随着波长的增加,波浪对水轮机极限载荷的增幅增加。相同工况条件、50 m波长时,波高每增加1 m,水轮机极限载荷增加27%。波浪对水轮机极限载荷的影响十分显著,在浮式电站运动响应分析及水轮机结构设计时,必须考虑波浪对水动力载荷的增幅。
[1]N Barltrop,K S Varyani,A Grant,et al.Investigation into Wave Current Interactions in Marine Current Turbines,Proc Inst Mech Eng Part A[J].Power Energy,2007,221(2):233-242.
[2]P W Galloway,LE Myers,A S Bahaj.Studies of a Scale Tidal Turbine in Close Proximity to Waves[C]//Third International Conference and Exhibition on Ocean Energy,2010.
[3]L Luznik,K A Flack,E E Lust,et al.The Effect of Surface Waves on the Performance Characteristics of a Model Tidal Turbine[J]. Renew Energy,2013,58:108-114.
[4]E Lust,Luksa Luznik,et al.The Influence of Surface Gravity Waves on Marine Current Turbine Performance[J].International Journal of Marine Energy,2013,3:27-40.
[5]Zhen Hu,Xiaoping Du.Reliability Analysis for Hydrokinetic Turbine Blades[J].Renewable Energy,2012,48:251-262.
[6]Faudot C,Dahlhaug O G.Prediction of Wave Loads on Tidal Turbine Blades[J].2012,20(0):116-133.
[7]盛其虎,周念福,张学伟,等.二维立轴水轮机强迫振荡水动力性能研究[J].哈尔滨工程大学学报,2015,36(1):41-45.
[8]Qihu Sheng,Fengmei Jinga,Liang Zhang,et al.Study of the Hydrodynamic Derivatives of Vertical-Axis Tidal Current Turbines in Surge Motion[J].Renewable Energy,2016,96:366-376.
Analysis on the Wave Loads of Floating Vertical Axis Tidal Turbines
SHENG Qi-hu1,LI Chao2,ZHANG Xue-wei1,SUN Ke1,JING Feng-mei1,MA Yong1
1.Ocean Technology Institute,Harbin Engineering University,Harbin 150001,Heilongjiang Province,China; 2.National Ocean Technology Center,Tianjin 300112,China
Sea waves can significantly affect the hydrodynamic performance of floating vertical axis turbine(VAT). An approximate formula based on the slender body theory is derived to calculate the hydrodynamic load of 3D VAT.The hydrodynamic loads of the fixed-blade VAT with two blades installed on the"Haineng-1"floating tidal current power station are calculated at the case of the same direction with currents and waves.The numerical results show that the hydrodynamic loads on turbine axis have two-period properties.On the working condition of the turbine,the maximum load increases by 27%when the wave height rises by 1 m.At the same wave height and working conditions,the maximum loads of the main axis increase with increasing wave length.
tidal current energy;vertical axis turbine;floating tidal energy power station;hydrodynamics;wave loads
P74;TK73
A
1003-2029(2016)05-0025-04
10.3969/j.issn.1003-2029.2016.05.005
2016-07-14
国家海洋能专项基金资助项目(GHME2013ZC01);国家自然科学基金资助项目(51409057,11572094,51309068,51209060,51309069)
盛其虎(1974-),男,副教授,主要研究方向为浮体水动力学,系泊系统动力学,海洋能利用。Email:shengqihu@hrbeu.edu.cn
——辽宁省博物馆藏中国古代立轴山水画展

