超高性能混凝土连续梁弯矩调幅系数
徐海宾, 邓宗才
(1. 河南理工大学 土木工程学院,河南 焦作 454000;2.北京工业大学 建筑工程学院,北京 100124)
超高性能混凝土连续梁弯矩调幅系数
徐海宾1, 邓宗才2
(1. 河南理工大学 土木工程学院,河南 焦作 454000;2.北京工业大学 建筑工程学院,北京 100124)
为了研究HRB500钢筋超高性能混凝土连续梁的弯矩调幅性能,依据非线性理论分析了超高性能混凝土连续梁弯矩调幅系数的计算方法,并编制了相应的程序,通过与已有试验结果的对比验证了程序的准确性。 通过对22根HRB500钢筋超高性能混凝土连续梁的模拟分析,计算了22根模拟梁在正常使用极限状态及承载能力极限状态下的弯矩调幅系数;根据模拟结果,提出以中支座截面相对受压区高度ξ为自变量的弯矩调幅系数β的计算公式为β= -3.541ξ+0.867;最后以正常使用极限状态下裂缝宽度不大于0.2 mm为控制条件,建议ξ≤0.13时β取0.4,ξ≥0.21时β取0.1,0.13<ξ<0.21时,β值采用直线内插求得。
超高性能混凝土;连续梁;非线性分析;弯矩调幅;HRB500钢筋;裂缝
超高性能混凝土(ultra-high performance concrete,UHPC)具有超高的强度、韧性以及优良的耐久性[1]。目前国内外对UHPC的配合比、养护条件、基本力学性能及耐久性进行了大量的试验研究,UHPC在一些试点工程中也得到了应用[2]。钢筋混凝土连续梁设计应考虑其内力重分布,“调幅法”因简单易行,方便设计,为各国规范普遍采用。迄今为止,针对普通钢筋混凝土连续梁的弯矩调幅已有大量研究[3]。由于UHPC的力学性能与普通混凝土有显著差异,其抗压强度、峰值压应变、极限压应变均比普通混凝土高很多,开裂后由于裂缝间钢纤维的桥联作用,受拉区混凝土并不退出工作等,使得UHPC连续梁的弯矩调幅性能明显不同于普通混凝土连续梁,然而目前对钢筋UHPC连续梁的弯矩调幅性能的研究鲜见报道。本文编制计算机程序对UHPC连续梁的弯矩调幅性能进行分析,并建议了其取值方法。
1 UHPC连续梁非线性分析
1.1 基本假定
1)截面变形符合平截面假定。
2)钢筋与混凝土之间粘结良好,不考虑粘结滑移。
3)不考虑剪切变形的影响。
4)不考虑混凝土收缩、徐变、温湿度变化等因素对结构内力和变形的影响。
1.2 材料本构关系
1)UHPC轴压应力-应变关系
根据文献[4],轴压应力-应变关系曲线如图1,图中fc为轴压强度,ε0为峰值压应变,εcu为极限压应变,取0.005。
σc=
(1)
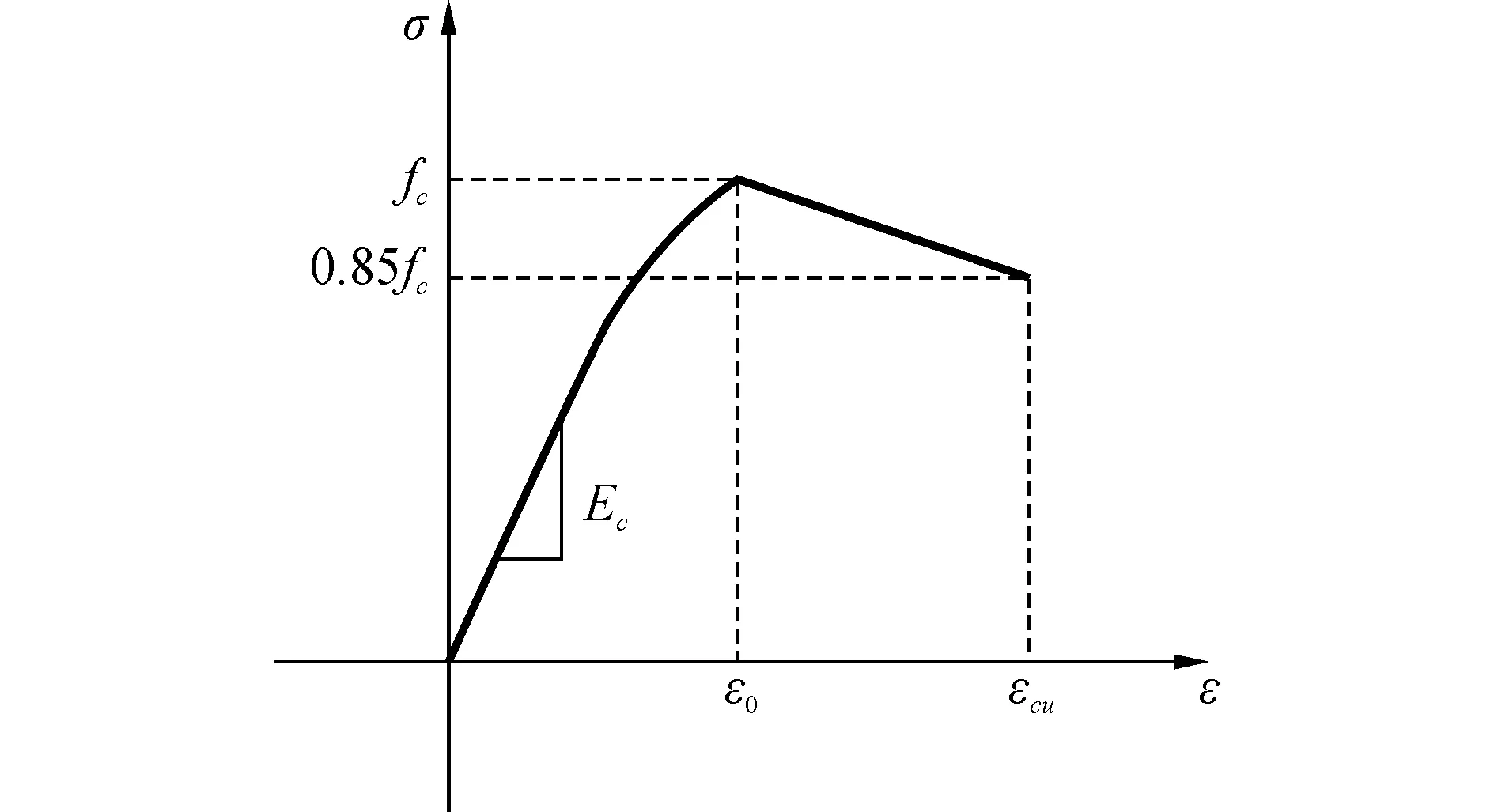
图1 UHPC轴压应力-应变关系曲线Fig.1 Axial compression stress-strain curve for UHPC
2)UHPC轴拉应力-应变关系
根据文献[5],采用简化的UHPC轴拉应力-应变关系,如图2所示。

图2 UHPC轴拉应力-应变关系曲线Fig.2 Axial tension stress-strain curve for UHPC
图2中ft为轴拉强度,εtc为开裂拉应变,ε0.3为裂缝宽度0.3 mm时的拉应变,εtu为极限拉应变。
(2)
(3)
(4)
式中:lf为钢纤维长度;lc为钢纤维特征长度,对T型和矩形截面可取梁高的2/3,mm。
3)钢筋应力-应变关系
钢筋应力-应变关系采用理想弹塑性模型,方程如下
(5)
式中:Es为钢筋弹性模量,εs为钢筋应变,fy为钢筋屈服强度,εy为钢筋屈服应变,εsu为钢筋极限拉应变。
1.3 截面弯矩-曲率关系曲线计算
此处利用条带积分法计算截面的弯矩-曲率关系,如图3所示,将梁截面沿梁高方向划分为相互平行的若干条带,假定每一条带单元上的应力为均匀分布,采用条带单元形心处的应力和应变代表该单元的应力和应变。
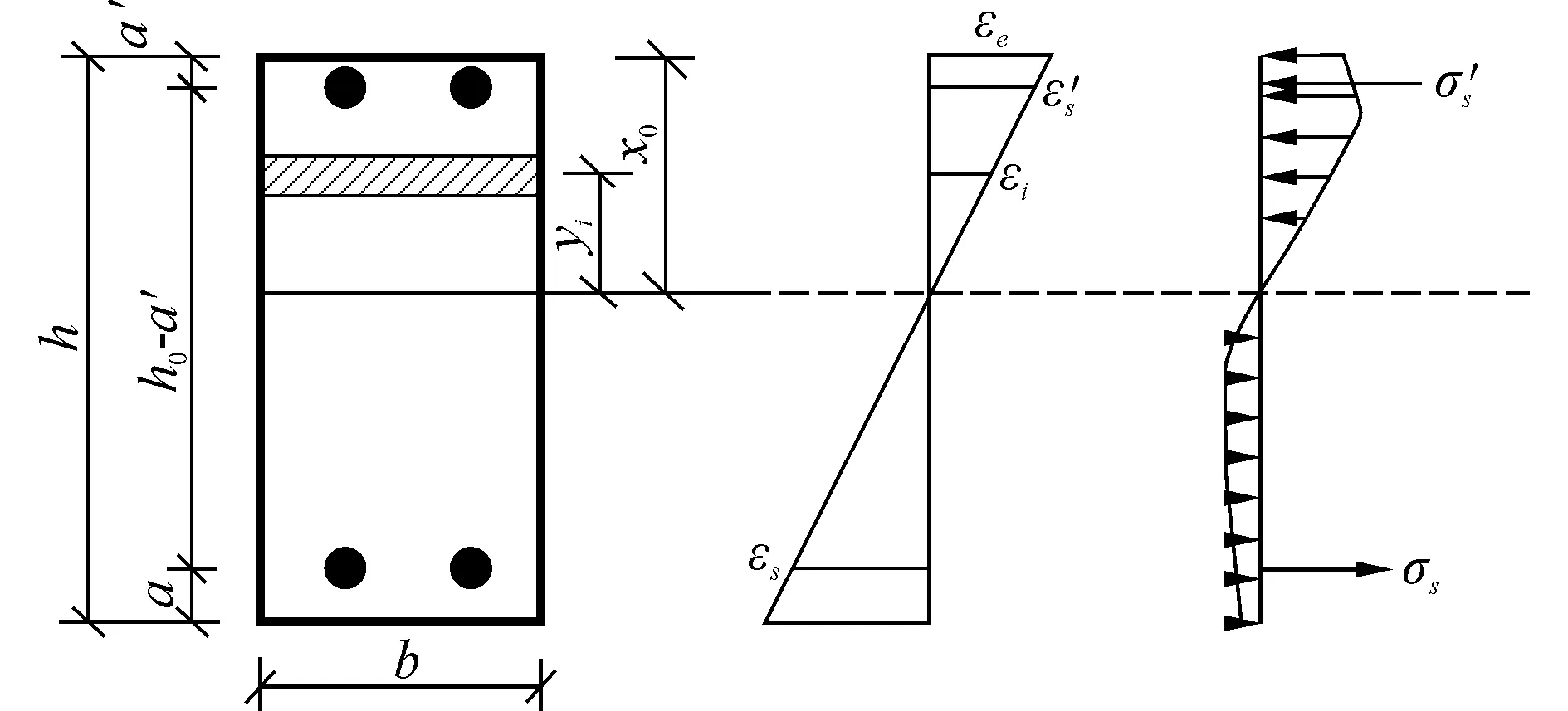
图3 截面划分及应力应变分布Fig.3 The section units division and distribution of stress and strain
对于给定的梁截面任意曲率φ,假定受压边缘混凝土的应变为εc,根据图3,由平截面假定,任意条带形心处应变为
(6)
式中:εi为第i条带形心处的应变;yi为第i条带形心至中性轴的距离;x0为中性轴高度。
受拉钢筋形心处的应变为
(h0-x0)
(7)
式中:ys为受拉钢筋形心至中性轴距离,h0为截面有效高度。
受压钢筋形心处的应变为
(x0-a′)
(8)

根据材料的本构关系,可得各条带形心及钢筋的应力:
σi=σ(εi)
(9)
由截面轴向力平衡有:
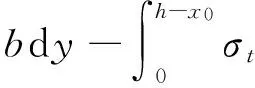
(10)

由截面力矩平衡有:
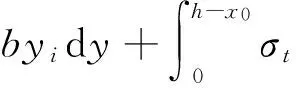

(11)
利用程序求解截面弯矩-曲率关系的步骤如下:
1)将截面划分成若干条带;
2)给定曲率φ=φ+Δφ;
3)假定梁截面受压边缘应变εc;
4)求各条带形心及钢筋的应变;
5)根据UHPC及钢筋的本构关系求与应变相对应的应力值;
6)根据式(10)验算轴力是否满足截面平衡条件;
7)若式(10)不满足,调整εc的值,重复步骤4~6,直至式(10)得到满足;
8)按式(11)求解内力弯矩,得到与φ所对应的弯矩M;
9)循环步骤2~8,得到完整的M-φ关系曲线。
1.4 弯矩调幅系数计算
弯矩调幅系数计算需要分别计算出连续梁的弹性内力和塑性内力,本文计算连续梁弹性内力时采用有限元程序Midas Civil 进行计算,塑性内力采用共轭梁法[6]编制程序进行计算,以两跨连续梁承受跨中集中荷载为例,分析步骤如下:
1)将梁沿跨径方向划分成若干微段;
2)令i=0,施加跨中集中荷载P=P0+iΔP;
3)令j=0,给定对应跨中荷载P的中支座支反力初始值Rm,Rm=Rm+jΔRm;
4)根据结构静力平衡和弯矩平衡,计算得到P对应的边支座反力Re,求解结构各截面弯矩值;
5)调用前期存储的各截面的M-φ关系曲线,根据各截面弯矩计算值,得到各截面曲率;
6)采用共轭梁法计算中支座处的竖向位移f;
7)检查中支座竖向位移f的误差是否满足要求,若满足,则所给定Rm即为P所对应中支座反力,否则,令j=j+1,重复步骤3~6,直至中支座竖向位移f 的误差达到要求,求解P所对应的中支座弯矩Mp;
8)利用Midas Civil计算P作用下连续梁中支座处弯矩弹性计算值Me;
9)计算P作用下连续梁中支座处弯矩调幅系数β=(Me-Mp)/Me;
10)令i=i+1,重复步骤2~9,可得各级荷载作用下的中支座弯矩调幅系数。
1.5 试验验证
为验证上述计算理论及程序的准确性,对文献[7]中的钢筋UHPC连续梁进行了对比计算。试验中钢纤维采用直径0.22 mm,长径比59.1的平直钢纤维,钢纤维体积掺量2%,实测UHPC棱柱体轴压强度为102.28 MPa,峰值应力对应应变为3 560×10-6,极限压应变5 500×10-6,弹性模量41 237 MPa。试验梁截面尺寸均为b×h=180 mm×220 mm,梁长3 400 mm,分两跨,采用两跨跨中集中荷载同步加载。
表1为各试验梁极限荷载以及中支座处弯矩调幅系数试验值与本方法计算值的对比,表中Pt、Pc分别为极限荷载试验值和计算值,βt、βc分别为弯矩调幅系数试验值和计算值,μ为平均值,CV为变异系数。
表1 文献[7]试验值与本文计算值对比
Table 1 Comparison of experimental values in reference [7] to calculated values in this paper

编号Pt/kNPc/kNPt/Pcβtβcβt/βcLL-13603501.030.240.211.14LL-23403361.010.280.281.00LL-33103130.990.370.430.86LL-42902950.980.590.541.09LL-52852781.030.630.690.91μ1.001.00CV0.020.12
由表1可知,按本文计算程序所得弯矩调幅系数计算值与试验值吻合较好,变异系数较小,说明本文计算程序具有较好的精度,可用于UHPC连续梁的弯矩调幅计算。
2 UHPC梁弯矩调幅系数分析
2.1 模拟梁设计
为了对超高性能混凝土连续梁的弯矩调幅性能进行分析,本文以中支座截面配筋面积和UHPC强度为变化参数,设计了22根矩形模拟梁。考虑超高性能混凝土宜与高强钢筋配合使用,因此本次模拟梁设计时纵向受力钢筋均选用HRB500钢筋,屈服强度取520 MPa,弹性模量取2.0×105MPa;受压架立筋选用2根公称直径6 mm的HRB235钢筋,纵向受拉钢筋合力点至梁截面受拉边缘的距离均取35 mm。模拟梁的基本参数为:b×h=200 mm×350 mm,单跨计算跨径1 800 mm,共两跨。加载方式采用在两跨跨中同步施加单点集中荷载的方法,如图4所示,其他参数选取见表2。

图4 模拟梁加载方法Fig.4 Load form of simulated beams

编号纵筋配置中支座跨中UHPC力学性能fc/MPaft/MPaEc/MPaLB14Φ256Φ251306.8946000LB23Φ256Φ251306.8946000LB32Φ256Φ251306.8946000LB44Φ206Φ251306.8946000LB53Φ206Φ251306.8946000LB62Φ206Φ251306.8946000LB78Φ166Φ251306.8946000LB86Φ166Φ251306.8946000LB94Φ166Φ251306.8946000LB103Φ166Φ251306.8946000LB112Φ166Φ251306.8946000LB126Φ106Φ251306.8946000LB134Φ186Φ251306.8946000LB146Φ256Φ251306.8946000LB154Φ25+2Φ166Φ251306.8946000LB164Φ25+2Φ206Φ251306.8946000LB174Φ256Φ251055.5741200LB183Φ256Φ251055.5741200LB194Φ166Φ251055.5741200LB206Φ256Φ251055.5741200LB214Φ25+2Φ166Φ251055.5741200LB224Φ25+2Φ206Φ251055.5741200
2.2 模拟梁结果及分析

以截面相对受压区高度ξ为横坐标,以弯矩调幅系数β为纵坐标,将各模拟梁计算值绘于图5中。
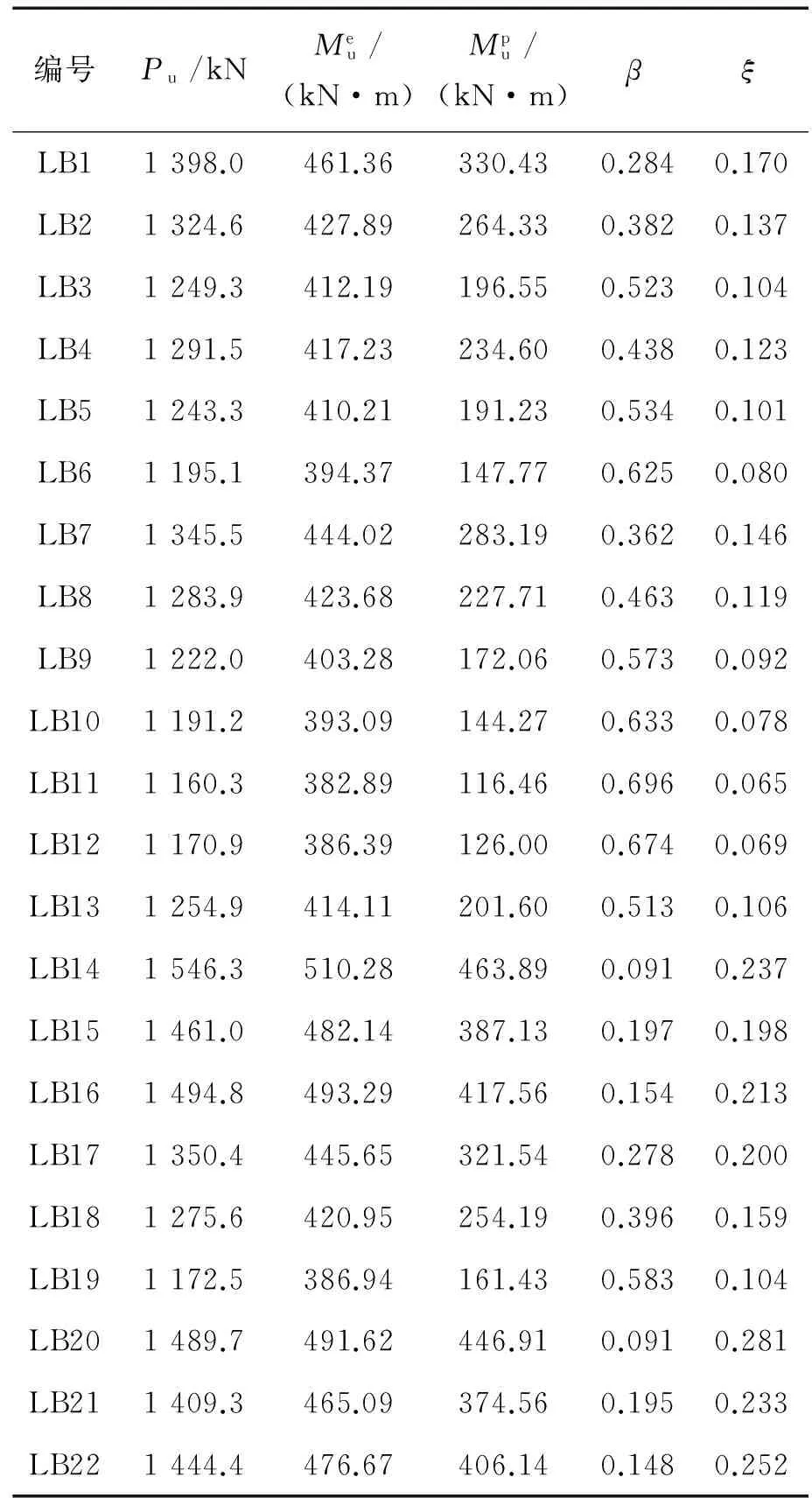
表3 模拟梁计算结果
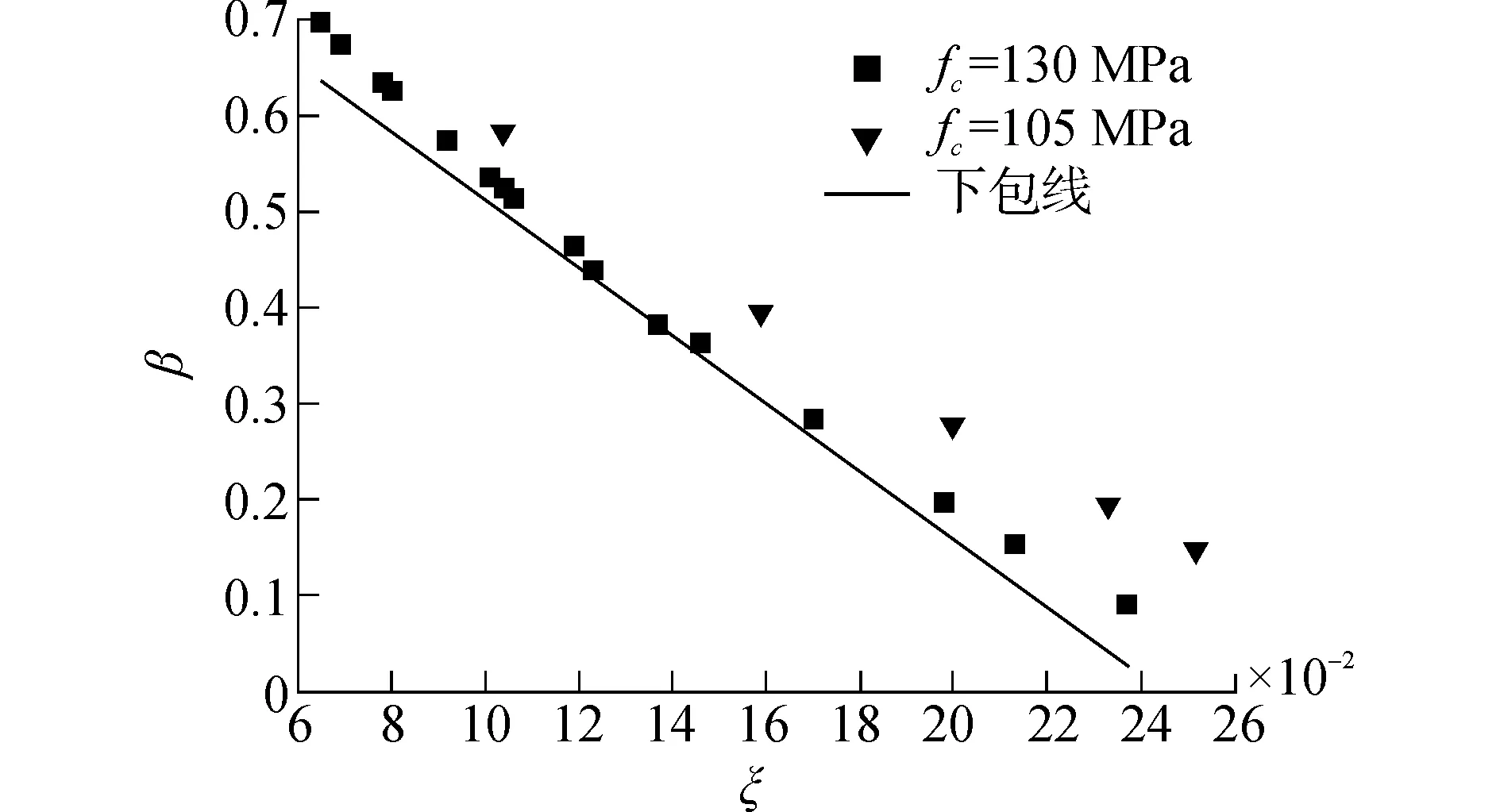
图5 ξ与β关系分布Fig.5 Relationship between ξ and β
由图5可知,截面弯矩调幅系数随相对受压区高度的增大而减小,二者近似呈线性关系;相对受压区高度不变时,截面弯矩调幅系数随混凝土强度的提高而减小。根据图中ξ与β关系点分布,可得到弯矩调幅系数β与中支座混凝土相对受压区高度ξ关系下包线。
根据弯矩调幅系数β与中支座混凝土相对受压区高度ξ关系下包线,可得以截面相对受压区高度ξ为自变量的中支座弯矩调幅系数β的计算公式为
β=-3.541ξ+0.867
(12)
结构设计不仅要满足结构的承载能力要求,而且要满足正常使用要求。设计时若取调幅系数过大,可能会造成正常使用阶段裂缝宽度超出规范限值,因此弯矩调幅系数的取值应考虑正常使用状态下满足裂缝宽度限值的问题。对以上模拟梁,偏保守的取0.6倍极限荷载作为正常使用极限状态所对应的荷载,计算正常使用极限状态下模拟梁中支座截面的弯矩及最大裂缝宽度,计算结果见表4,表中Psls为正常使用极限状态所对应的荷载,Msls为中支座截面在正常使用极限状态下所对应的弯矩,wsls为正常使用极限状态下的最大裂缝宽度。

表4 正常使用极限状态下最大裂缝宽度
根据文献[8],最大裂缝宽度计算采用下式:
(13)
αcr=τlτsαc
(14)
式中:αcr为构件受力特征系数;ψ为钢筋应变不均匀系数;σs为纵向受拉钢筋等效应力;lcr为平均裂缝间距;βwf为裂缝修正系数,取0.35;λf为钢纤维含量特征值;τl为长期效应系数;τs为最大裂缝宽度与平均裂缝宽度的比值,取1.66;αc为受拉混凝土平均应变影响系数,取0.77。
目前缺乏超高性能混凝土长期性能的研究资料,考虑超高性能混凝土裂缝间钢纤维桥联作用对裂缝扩展的抑制作用,超高性能混凝土的长期性能应较普通混凝土好,因此采用上式计算最大裂缝宽度时,长期效应系数偏安全的取与普通混凝土相同,即取τl=1.5。
根据表4,以弯矩调幅系数β为横坐标,正常使用极限状态下最大裂缝宽度wsls为纵坐标,绘出β与wsls的对应关系如图6所示。
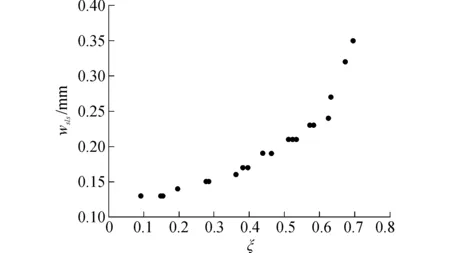
图6 β与wsls关系分布图Fig.6 Relationship between β and wsls
由图6可知,随着弯矩调幅系数β的增大,正常使用极限状态下最大裂缝宽度增大,且弯矩调幅系数越大,最大裂缝宽度增速越明显。当弯矩调幅系数不大于0.45时,正常使用极限状态下最大裂缝宽度小于0.2 mm;弯矩调幅系数介于0.45~0.6时,最大裂缝宽度介于0.2~0.25 mm;弯矩调幅系数大于0.6以后,最大裂缝宽度快速增大。
考虑正常使用极限状态最大裂缝宽度限值为0.2 mm,对配置HRB500钢筋、轴心抗压强度介于100~130 MPa的超高性能混凝土梁,建议弯矩调幅限值为
3 结论
1)以非线性方法分析了计算UHPC连续梁弯矩调幅系数的方法,并编制了计算程序。
2)通过对22根HRB500钢筋超高性能混凝土连续梁的数值分析,得到了22根模拟梁在跨中集中荷载作用下达到极限承载力时的弯矩调幅系数,拟合了以截面相对受压区高度为自变量的弯矩调幅系数计算公式。
3)以正常使用极限状态最大裂缝宽度不大于0.2 mm为限值,建议了HRB500钢筋超高性能混凝土梁的弯矩调幅系数取值方法。
[1]GRAYBEAL B, TANESI J. Durability of an ultrahigh performance concrete[J]. Journal of materials in civil engineering, 2007, 19(10): 848-854.
[2]CRANE C K. Shear and shear friction of ultra-high performance concrete bridge girders[D]. Georgia State: Georgia Institute of Technology, 2010.
[3]周基岳, 曾庆余. 弯矩调幅对钢筋混凝土连续梁使用阶段裂缝和挠度影响的试验研究[J]. 重庆建筑工程学院学报, 1991, 13(3): 68-79. ZHOU Jiyue, ZENG Qingyu. Experimental research of the moment modulation influence on cracking and deflection of continuous reinforced concrete beams under service loads[J]. Journal of Chongqing institute of architecture and engineering, 1991, 13(3): 68-79.
[4]徐海宾, 邓宗才. 预应力超高性能钢纤维混凝土梁受弯性能试验研究[J]. 建筑结构学报, 2014, 35(12): 58-64. XU Haibin, DENG Zongcai. Experimental research on flexural behavior of prestressed ultra-high performance steel fiber concrete beams[J]. Journal of building structures, 2014, 35(12): 58-64.
[5]AFGC. Ultra high performance fiber-reinforced concrete. Interim recommendations[M]. France: AFGC Publication, 2002: 25-26.
[6]何政, 欧进萍. 钢筋混凝土结构非线性分析[M]. 哈尔滨: 哈尔滨工业大学出版社, 2007: 260-275. HE Zheng, OU Jinping. Nonlinear analysis of reinforced concrete structure[M]. Harbin: Harbin Institute of Technology Press, 2007: 260-275.
[7]李莉, 郑文忠. 活性粉末混凝土连续梁塑性性能试验[J]. 哈尔滨工业大学学报, 2010, 42(2): 193-199. LI Li, ZHENG Wenzhong. Experimental study on plastic property of reactive powder concrete continuous beams[J]. Journal of Harbin institute of technology, 2010, 42(2): 193-199.
[8]徐海宾, 邓宗才. UHPC梁开裂弯矩和裂缝试验[J]. 哈尔滨工业大学学报, 2014, 46(4): 87-92. XU Haibin, DENG Zongcai. Cracking moment and crack width of ultra-high performance concrete beams[J]. Journal of Harbin institute of technology, 2014, 46(4): 87-92.
Moment redistribution coefficient of ultra-high performance concrete continuous beams
XU Haibin1, DENG Zongcai2
(1. School of Civil Engineering, Henan Polytechnic University, Jiaozuo 454000, China; 2. College of Architecture and Civil Engineering, Beijing University of Technology, Beijing 100124, China)
This research analyzes the calculation method of the moment redistribution coefficients of the ultra-high performance concrete (UHPC) continuous beams based on nonlinear theory to study the moment redistribution performance of the HRB500-reinforced UHPC continuous beams. A calculation program is also compiled. The program accuracy is verified by comparing the results derived herein with the existing test results. The moment redistribution coefficients of 22 simulated HRB500-reinforced UHPC continuous beams are obtained through a numerical analysis under normal service and ultimate load limit states. The simulation results show the formula for the moment redistribution coefficients asβ= -3.541ξ+0.867, where the independent variableξis equal to the relative height of the compressive region of the intermediate support section. Considering the limit of the maximum crack width to be less than 0.2 mm in the serviceability limit states,βis suggested to be equal to 0.4 whenξis less than or equal to 0.13.βis equal to 0.1 whenξis greater than or equal to 0.21. Moreover,βis calculated using a linear interpolation method whenξis greater than 0.13 and less than 0.21.
ultra-high performance concrete; continuous beam; nonlinear analysis; moment redistribution; HRB500 bar; crack
2015-09-21.
日期:2016-05-27.
国家自然科学基金项目(51378032);河南省高等学校重点科研项目(16A560021).
徐海宾(1979-), 男, 讲师,博士; 邓宗才(1961-), 男, 教授,博士,博士生导师.
邓宗才,E-mail:dengzc@bjut.edu.cn.
10.11990/jheu.201509060
TU529.5
A
1006-7043(2016) 11-1520-06
徐海宾, 邓宗才. 超高性能混凝土连续梁弯矩调幅系数[J]. 哈尔滨工程大学学报, 2016, 37(11): 1520-1525. XU Haibin, DENG Zongcai. Moment redistribution coefficient of ultra-high performance concrete continuous beams[J]. Journal of Harbin Engineering University, 2016, 37(11): 1520-1525..
网络出版地址:http://www.cnki.net/kcms/detail/23.1390.u.20160527.1354.018.html

