含无理式最值问题的解法梳理

李保勤

（山西省吕梁市高级实验中学）

含无理式最值问题的解法梳理

李保勤

（山西省吕梁市高级实验中学）

函数的最值问题是高中数学的重点和难点，也是高考的热点，而含无理式的函数最值问题往往是学生在这方面的弱点，总结该类型的常用解法很有必要。

无理函数；单根号；双根号；最值

一、单根号无理函数最值问题的求法

（一）判别式法：此法要由Δ≥0计算出y的范围后，还要注意求原函数定义域限制下y的范围，最后通过二者结合，求出原函数的最值，以免产生“增值”“误判”等情况.

两边平方整理，得2x2-（2y+1）x+y2=0.

∵x∈R，∴Δ=（2y+1）2-8y2≥0，解得.

（二）换元法：通过巧妙地对函数自变量换元，转换为我们比较熟悉的函数，化繁为简，化难为易，进而求函数最值.

∴y=2（1-t2）+4t=-2（t-1）2+4（t≥0）.

故ymax=4.

二、双根号无理函数最值问题的求法

（一）配方法：通过恰当配方，可以去根号，转化为有理式

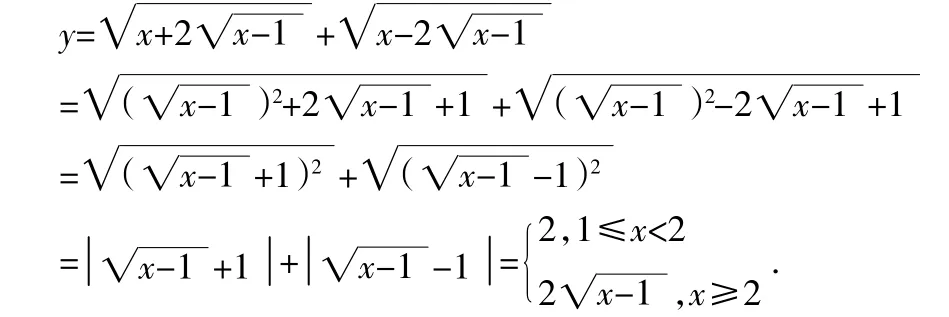
故ymin=2

例5.求函数的最小值.

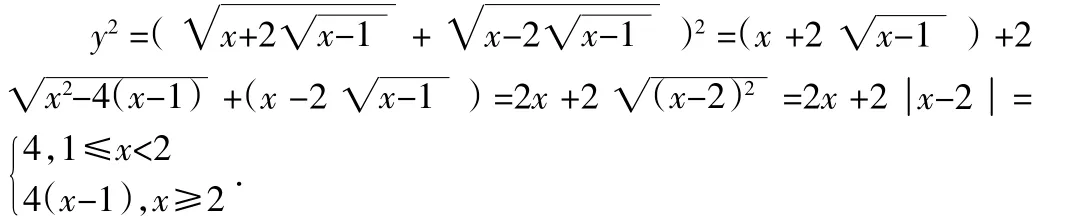
由于y2最小值为4，故ymin=2

（三）单调性法：把原函数分解为两个（或多个）新函数，根据两个（或多个）新函数在公共定义区间内的单调性，求原函数在每一区间上的最值，最后总结原函数在整个定义域上的最值.

综上可得，f（x）min=f（2）=

（四）几何法：利用两点距离公式，将函数的最值问题转化为求一动点到两定点距离和（差）的最值问题.

解：原函数转化为

（五）构造法：通过构造向量数量积等将函数最值转化为三角函数的最值，这要用到向量数量积的定义和坐标表示相关知识.

故yman=，ymin=2

·编辑王亚青

李保勤，男，硕士研究生，山西省吕梁市高级实验中学年级主任。