基于太阳阴影轨迹的经纬度估计研究

王　扉，胡永彪，丁　玲



基于太阳阴影轨迹的经纬度估计研究

王扉，胡永彪，丁玲

（湖南城市学院，湖南益阳 413000）

本文针对视频文件的拍摄地点及日期的估计问题，根据天文学知识，建立了影子长度和方位角针随观测地经纬度、观测时间变化的参数模型。对已知观测日期和未知观测日期的两种情形，以影子长度的比和影子方位角的差总体误差最小为目标，分别构建了两个优化模型。数值试验验证了所给模型与算法的可行性。

太阳高度角；太阳方位角；地理位置；多目标规划

现代科技的发展使得人们能够更为方便地记录高质量的视频文件。在分析视频材料时，有时需要确定视频的拍摄地点及日期，而利用天文学知识，对视频物体中的太阳影子变化进行分析是确定视频拍摄地点及日期的一种有效方法。

通过对视频进行图像处理，可得出各个时刻直杆的太阳影子顶点坐标。难点在于通过所得出的坐标数据找出视频拍摄的地点和日期。需要我们建立在地球不同地点（经纬度）、不同日期时刻下，描述物体影子长度变化规律的数学模型，进而基于所建模型给出视频拍摄日期和可能的地点。

1 影子随时间变化模型

首先，我们建立一个物体影子长度和方位角随着时间变化的数学模型。

假设地球是圆球体， 观测点附近地面水平，太阳照射地球为直线照射，不考虑大气折射所引起的误差和每日早晨和黄昏时候太阳高度角的假视。

太阳高度角和方位角是表征太阳位置的参数，确定了阳光对于地球表面任意一点的来向。如图1所示，太阳高度角是太阳(视为一质点O)与地球表面任意一点P的连线与过P点的地平面之间的夹角，记为;太阳方位角是上述连线在过P点的地平面上的投影线与地平面上过P点正南方位线的夹角，记为。

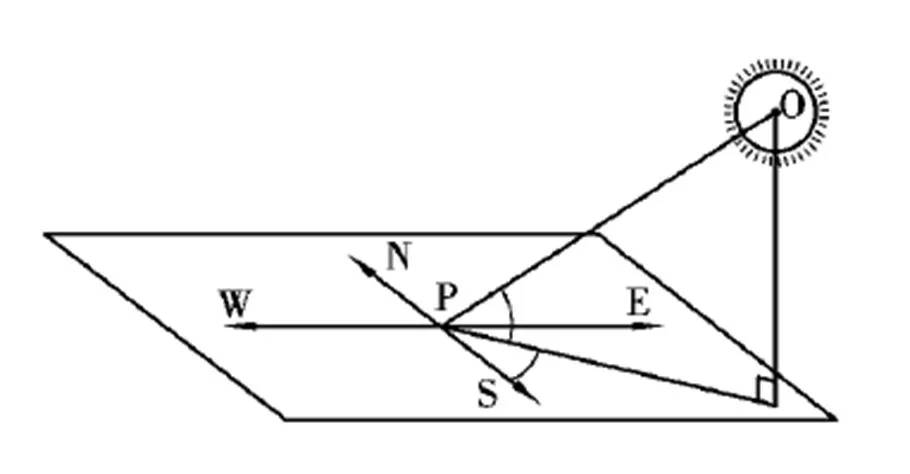
图1 太阳高度角和方位角的空间视图

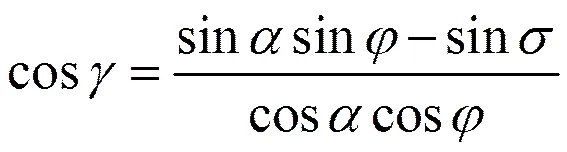
太阳赤纬是指太阳的直射纬度，即地球赤道平面与太阳和地球中心的连线之间的夹角。太阳赤纬角可由下列公式求得[2]，单位为度，准确度＜0.035：

太阳时角是过P点的经度平面和太阳所在经度平面之间的夹角。太阳连续两次上中天的时间间隔叫做真太阳日，1真太阳日分为24真太阳时。真太阳时12点时，太阳正好通过当地子午线，此时的影长最短。故通常以当地真太阳时12点对应的太阳时角为零，每隔一时区相差15度来计量太阳时角，即

其中为真太阳时。

日常生活中所使用的时间是平太阳时。真太阳时与平太阳时的差值称为时差。时差的计算方法如下[3]，单位为分钟：

综上所述，太阳高度角为

方位角通常以南点为0°，向西为正值，向东为负值。故

(8)

将(6)代入(8)得影长随时间变化关系：

以直杆底端为原点，水平地面为xy平面，正东方向为x轴正方向，正北方向为y轴正方向，建立一平面直角坐标系。则影子末端点的坐标为

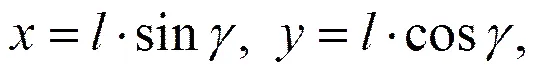
2 经纬度估计模型

下面，我们考虑这样一个问题：假设一直杆垂直于地面，以直杆底端为原点，水平地面为xy平面建立一平面直角坐标系。已知一组影子末端坐标随时间变化的数据，如何估算观测地的经纬度？

我们分两种情形考虑，问题1：已知观测日期，求观测地的经纬度；问题2：未知观测日期，观测地的经纬度和观测日期。

问题1：已知观测日期的经纬度估计

因为已知观测年、月、日，则由式(1)-(4)可计算出赤纬度和时差。问题1可转化为关于影子长度比与方位角差的误差的加权平方和的优化问题：

由几何知识易知在同一经线圈上必存在两点使得它们的太阳高度角相同。以影子长比的误差为目标函数（），只考虑到影子长度随着时间变化规律，理论上有两个不同纬度的最优解；而以影子方位角差的误差为目标函数（）考虑到影子随着时间旋转方向，北半球地平面上影子一般是顺时针方向变化，而南半球地平面上影子是逆时针方向变化，故理论上只有唯一解。

该问题的目标函数和约束函数的梯度较难计算，故可以采用直接法求解，例如单纯形法，参见[4]。求解模型(11)的具体算法如下：

算法1（已知观测日期的经纬度估计）

第1步初始化，按(9)和(10)，由给定观测时间和坐标计算影长比和方位角差；

第2步按(1)、(2)和(4)，由给定观测日期计算积日，赤纬和时差；

第3步用二次多项式拟合估计初始经度；

第4步用单纯形法求模型(11)的近似最优解。

说明：除南北极附近以外，影长随时间的变化均是由日出时影长无限大缩短到当地正午最短影长，然后再增长到日落时无限大。由于影长的变化规律的对称性，可以用二次线拟合观测时间和数据。设影长关于时间的拟合曲线最小值点为，以为当地正午北京时间近似值，则由(5)得，当地经度约为

经过实验发现，当观测到的影长变化率成线性（10-14点左右太阳）时，拟合二次曲线的极小点与当地正午误差较小，当观测到的影长变化较显著（8-9点或15-16点太阳）时，拟合二次曲线的极小点可以加上或减去1小时的修正量来估计当地正午时刻，当观测到的影长变化特别显著（6-7点或17-18点太阳）时，二次曲线拟合就会严重失真。

问题2：未知观测日期的经纬度估计

类似于问题1的讨论，问题2可归结为如下非线性优化问题：

由于一年中太阳在南北回归线来回摆动，赤纬角和时差的变化呈周期性，一年中通常存在两日太阳的赤纬角和时差相同，从而太阳高度角和方位角也相同，使得模型(12)存在两个局部极小值点。

模型(12)是一个整数混合优化问题，很难直接求解，我们采用对积日双层遍历搜索方法。

算法2 （已知观测日期的经纬度估计）

第一步按积日从6开始每增加10日调用算法1，求得总体误差最小和次小对应的经纬度和积日；

第二步再分别对该两个积日前后5天进行搜索，并以第一次搜索所得经纬度为初值调用算法1，最终得出总体误差最小的经纬度和积日。

3 数值实验

为了验证我们前面所提出的模型和及其求解方法的可行性。我们对三次不同测量数据进行了验证，数据来源于2015年全国大学生数学建模竞赛A题。

例1设直杆垂直于地面，坐标系以直杆底端为原点，水平地面为xy平面。测量时间为北京时间，坐标单位为米。

测量1：日期2015年4月18日，地点是(109.5°E， 18.3°N)；

测量2：日期2015年7月20日，地点是(79.75°E， 39.52°N)；

测量3：日期2015年1月20日，地点是(110.25°E， 29.39°N)。

观测数据参见2015A题附件[5]。算法1中单纯形法可用MATLAB中指令fminsearch实现。

算法1的结果如表1所示，数值实验结果表明在已知观测日期时，除对于测量2，μ=1以外，算法1能有效反求出观测地点。

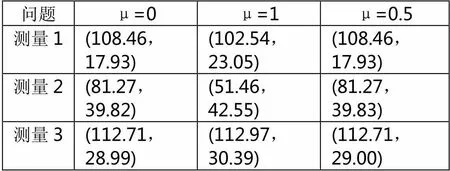
表1 算法1求出的测量地点（经纬度单位：度）

算法2的结果如表2所示，数值实验结果表明，算法2能较好地估计出观测地经纬度，而对于观测日期的估计，以影子方位角差的误差为目标函数（）结果比以影子长比的误差为目标函数（）的结果要好，而综合考虑两者（）的结果最佳。

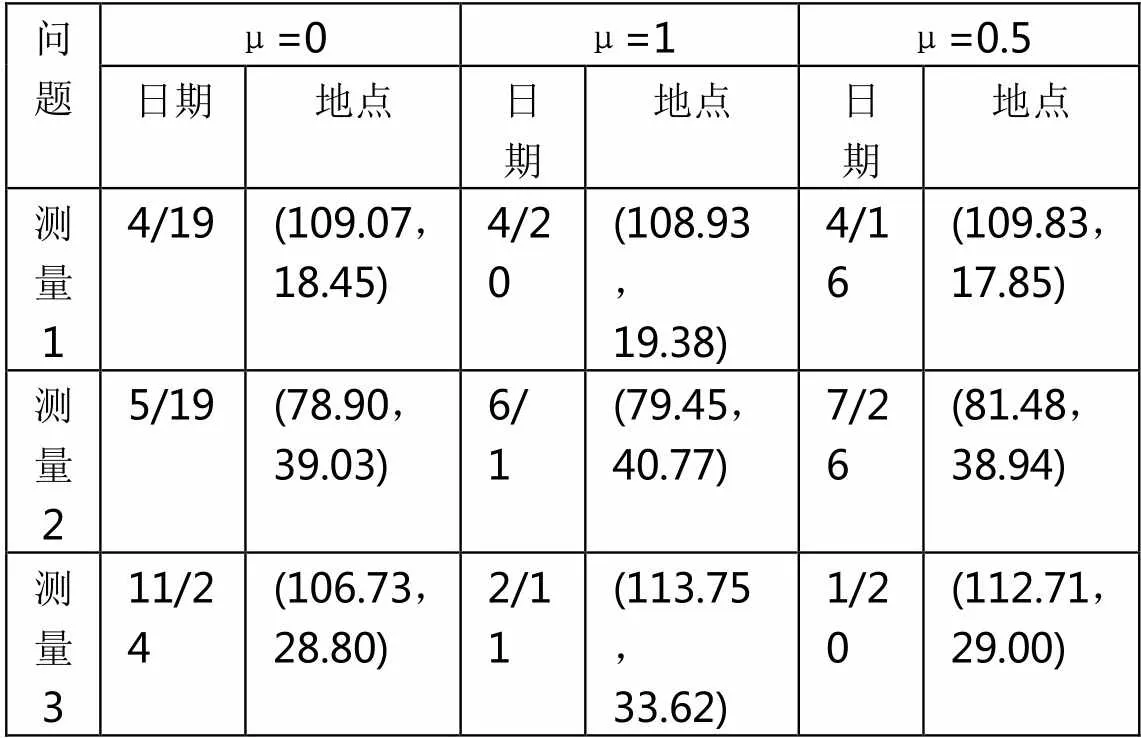
表2 算法2求出的测量日期和地点（日期：月/日，经纬度单位：度）

结果的误差主要来源于模型中太阳高度角和方位角计算忽略了大气对太阳光线的折射影响和赤纬与时差的近似计算。

4 结束语

本文研究了利用太阳影子轨迹确定观测地点和观测日期的问题，当已知观测日期时，构建了一个关于经纬度的非线性多目标规划模型，当示知观测日期时，构造了一个混合整数规划模型。针对两个模型，提出了相应算法，数值实验验证了模型的可行性和算法的有效性。模型构建过程中作了适当简化假设，但对结果的影响可以忽略。

[1]王炳忠，刘庚山.日射观测中常用天文参数的再计算[J]，太阳能学报，1991，12(1)，27-32.

[2]John A.Duffie， William A. Beckman. solar engineering of thermal processes[M]. Hoboken， NJ :John Wiley & Sons，2006.

[3]G.N. Tiwari. Solar energy :fundamentals， design， modelling and applications[M]. Boca Raton， FL:CRC Press，2002.

[4]袁亚湘. 非线性优化计算方法[M]. 科学出版社，2008.02.

[5]2015年全国大学生数学建模竞赛赛题， http://www.mcm.edu.cn/html_cn/ node/ac8b96613522ef62c019d1cd45a125e3.html， 2015-09-12.

Geo-location estimation from the solar shadow

WANG Fei, HU Yong-biao, DING Ling

(Hunan City University, Hunan Yiyang 413000)

The paper is to estimate the location and date of the video file. According to the knowledge of astronomy, a parameter model of the length and azimuth angle of the shadow is established. For two cases of known observation date and unknown date, two optimization model of minimizing the total error of the ratio of the shadow length and the difference of the shadow azimuth is presented. Numerical experiments verify the feasibility of the models and the algorithms.

Solar altitude; Solar azimuth; Geographical location; Multi-objective programming

（责任编辑：雷 君）

P127

A

10.3969/j.issn.1672-7304.2016.06.016

1672–7304(2016)06–0033–04

王扉（1971-），男，湖南益阳人，博士，讲师，研究方向：最优化理论与方法。