两参数Birnbaum-Saunders疲劳寿命分布的统计分析方法研究
王蓉华,徐晓岭,顾蓓青
(1.上海师范大学 数理学院,上海200234;2.上海对外经贸大学 商务信息学院,上海201620)
两参数Birnbaum-Saunders疲劳寿命分布的统计分析方法研究
王蓉华1,徐晓岭2,顾蓓青2
(1.上海师范大学 数理学院,上海200234;2.上海对外经贸大学 商务信息学院,上海201620)
文章首先比较了全样本场合下两参数BS疲劳寿命分布各种参数的点估计的优劣,认为当样本容量较大时,用分位数估计更为方便。通过Monte Carlo模拟说明文献[6]关于尺度参数的区间估计有可能是不存在的。
两参数Birnbaum-Saunders疲劳寿命分布;点估计;区间估计;尺度参数
0 引言
Birnbaum-Saunders模型[1]是概率物理方法中的一个重要失效分布模型,这个模型是Birnbaum和Sauders在1969年研究主因裂纹扩展导致的材料失效过程中推导出来的,这一模型在机械产品可靠性研究中应用广泛,主要应用于疲劳失效研究,对于电子产品性能退化失效分析也有重要应用。
设X服从两参数Birnbaum-Saunders疲劳寿命分布BS(α,β),其分布函数F(x)与密度函数分别为:

其中,α>0称为形状参数,β>0称为刻度参数(或者称为尺度参数),φ(x),Φ(x)分别为标准正态分布的密度函数与分布函数,即
由于Birnbaum-Saunders疲劳寿命分布是从疲劳过程的基本特征出发导出的,因此它比常用寿命分布如威布尔分布和对数正态分布更适合描述某些由于疲劳而引起失效的产品寿命规律。此分布已经成为可靠性统计分析中的常用分布之一。
1 参数的几种点估计方法的综合比较
1.1参数的极大似然估计(方法一)
设X1,X2,…,Xn为来自Birnbaum-Saunders疲劳寿命分布总体X~BS(α,β)的一个容量为n的简单随机样本,其次序观察值为x1,x2,…,xn。
似然函数为:

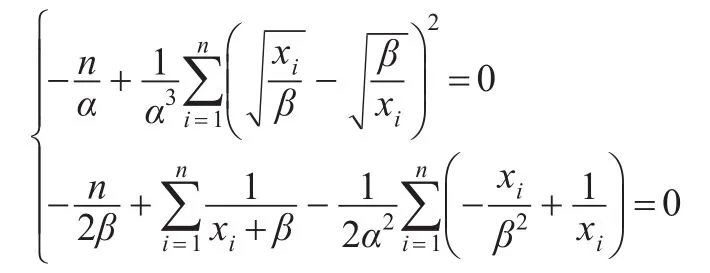
化简得仅含参数β的超越方程:

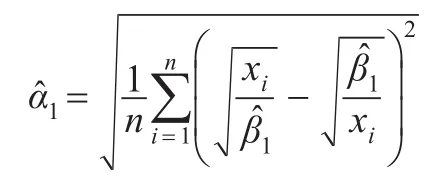
极大似然估计需要解非线性方程组,且计算较为复杂。由文献[2]可知,当α>2时,似然函数有多个极大值点。
1.2矩估计(方法二)

表1 100000次模拟中满足的频率
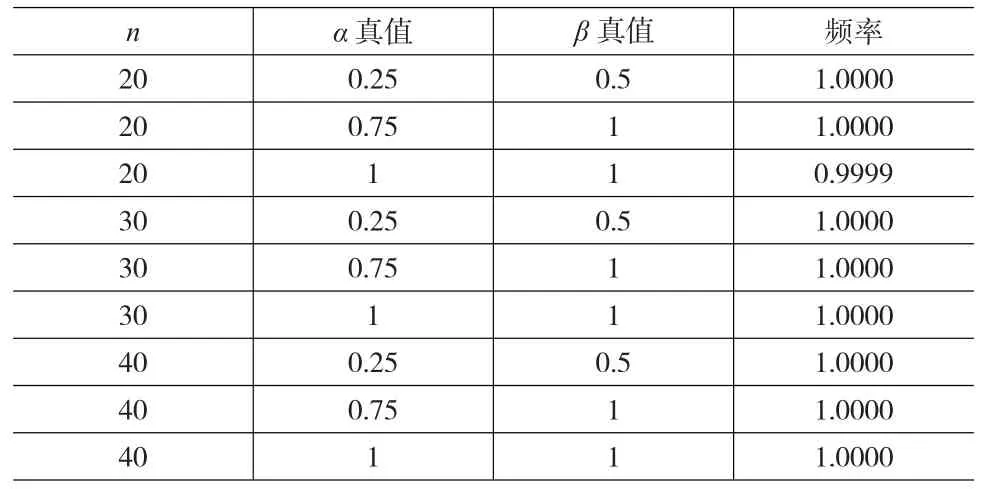
表1 100000次模拟中满足的频率
n 20 20 20 30 30 30 40 40 40 α真值0.25 0.75 1 0.25 0.75 1 0.25 0.75 1 β真值0.5 1 1 0.5 1 1 0.5 1 1频率1.0000 1.0000 0.9999 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000
由此可以看出当α,β取值较小时矩估计1是可行的。
1.3矩估计(方法三)
由于X-1~BS(α,β-1),于是可列矩方程组:

1.4逆矩估计(方法四)

由于独立同分布,服从于N(0,1),由逆矩估计思想建立如下方程:

化简可得参数β,α的逆矩估计分别为:

1.5分位数估计(方法五)
1.6回归估计方法(方法六)
孙祝岭在文献[3]中利用回归分析模型,给出了参数的最小二乘估计如下:

1.7六种点估计的模拟比较
取样本容量n=15,20,30,40,给定参数α,β真值,通过10000次模拟,分别计算其六种点估计的均值和均方误差,模拟结果如表2所示:

表2 六种估计方法的模拟比较

续表2
从模拟结果来看,α,β真值较小的时候效果较好,并且这几种方法的效果也相近,方法二的精度稍差些。当样本容量n较大时,分位数估计的效果要好些,尤其是对参数α的估计较为精确,同时分位数估计计算也较为方便,适合工程应用。
例1[3]:设总体X~BS(α,β),来自X的为10的样本观察值为:1401.7,2170.3,3762.9,414.0,650.7,441.0,902.8, 806.6,1292.1,760.3,计算α,β的估计值。
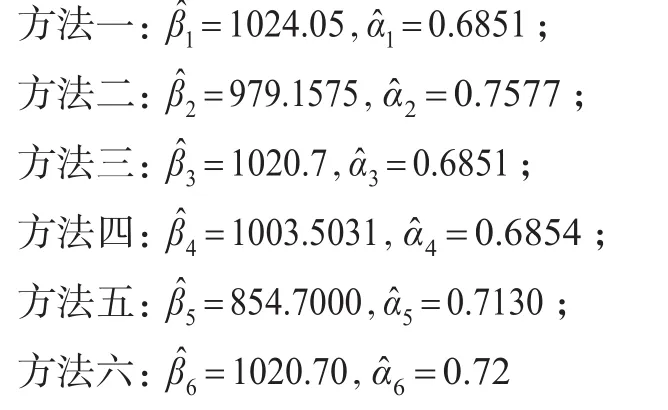
例2[4]:数据来自Bjerkedal(1960),也被Guptaetal(1997)分析过。数据表示几内亚猪注射不同剂量的结核杆菌的生存时间。对于文中的养殖方法,有72个观测值如下:
12,15,22,24,24,32,32,33,34,38,38,43,44,48,52,53,54,54,55,56,57,58,58,59,60,60,60,60,61,62,63,65,65,67,68,70,70,72,73,75,76,76,81,83,84,85,87,91,95,96,98,99,109,110,121,127129,131,143,146,146,175,175,211,233,258,258,263,297,341,341,376.
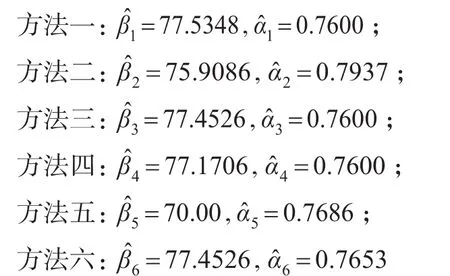
例3[5]:碳纤维的破坏应力(GPa)如下所示:

2 文献[6]关于参数β的区间估计的讨论
设X1,X2,…,Xn为来自Birnbaum-Saunders疲劳寿命分布总体X~BS(α,β)的一个容量为n的简单随机样本,其次序观察值为x1,x2,…,xn。



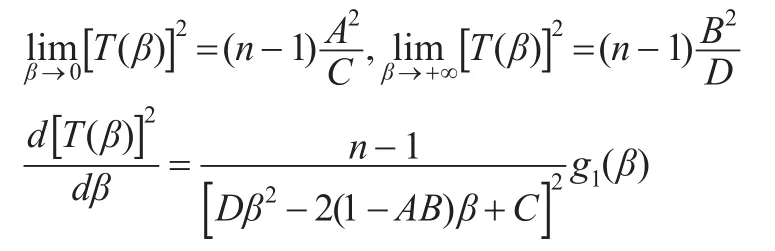

又:
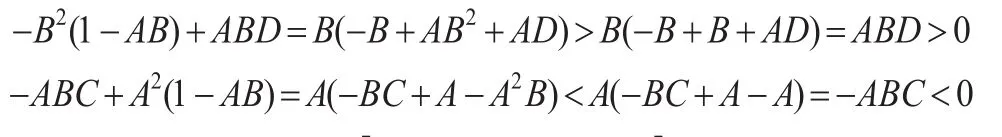
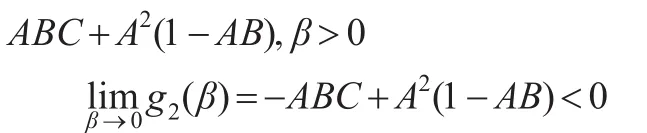
则针对函数 g2(β),存在 β0>0,且当0<β<β0时,g2(β)<0;当β>β0时,g2(β)>0
记:

也即,当0<β<β0时严格单调下降;当β>β0时严格单调上升。

表3 1000次Monte Carlo模拟比较
[1]Birnbaum Z W,Saunders S C.A New Family of Life Distribution[J]. Appl.Prob,1969,(6).
[2]王炳兴,王玲玲.Birnbaum-Saunders疲劳寿命分布的参数估计[J].华东师范大学学报,1996,(4).
[3]孙祝岭.Birnbaum-Saunders疲劳寿命分布参数的回归估计方法[J].兵工学报,2010,31(9).
[4]Kundu D,Kannan N,Balakrishnan N.On the Hazard Function of Birnbaum-Saunders Distribution and Associated Inference[J].Compu⁃tational Statistics&Data Analysis,2008,(52).
[5]Gauss M,Cordeiro A.Lemonte J.TheβBirnbaum-Saunders Distribu⁃tion:An Improved Distribution for Fatigue Life Modeling[J].Computa⁃tional Statistics and Data Analysis.2011,(55).
[6]孙祝岭.Birnbaum-Saunders疲劳寿命分布尺度参数的区间估计[J].兵工学报,2009,30(11).
(责任编辑/易永生)
O212
A
1002-6487(2016)22-0027-04
国家自然科学基金资助项目(11671264);全国统计科学研究计划重点项目(2013LZ08);上海市教育委员会科研创新一般项目(14YZ080)
王蓉华(1972—),女,上海人,博士,副教授,研究方向:应用统计。

