在真实环境中纠缠动力学的非马尔科夫效应

詹强+李铭仕+叶智婷+叶广源+刘振考+王世洪+黄江

Abstract By considering the influence of the environmental disorder in the non-local decoherence system， the non-Markovian entanglement dynamics of two independent qubits was investigated. With the simulation of the environment noise as external entities， the preservation of entanglement depends on the environmental disorder was found. Its corresponding physical mechanism is also given.

Key words non-Markovian； entanglement； non-local

中图分类号 O413.2 文献标识码 A 文章编号 1000-2537（2016）05-0065-05

摘 要 在非局域退相干系统中，研究了环境紊乱程度对两体非马尔科夫纠缠动力学的影响.通过模拟环境的噪声，发现了纠缠保持依赖与环境的紊乱程度.并给出了相应的物理机制.

关键词 非马尔科夫；纠缠；非局域

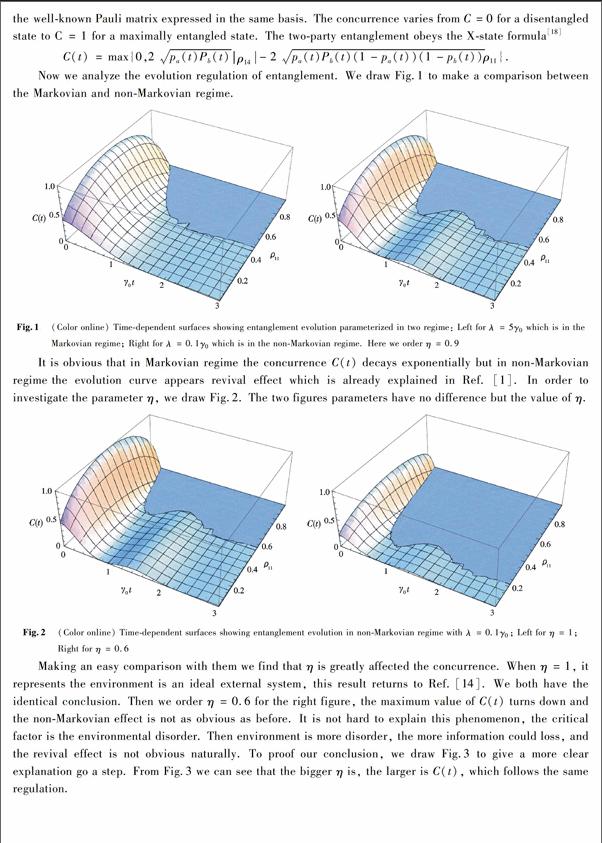
All realistic quantum systems are unavoidable to interact with its environments that occurs the so-called dissipation and decoherence， the dissipation and decoherence quantum dynamics of quantum cavities have been studied for decades because it is the bases of quantum communication and information[1-5]. Taking into account the influence of the environment on the quantum dynamics evolution makes the systems more complicate and interesting[6-7]. We can mainly classify the quantum dynamical processes into Markovian processes with no memory effect and non-Markovian processes with memory effect， according to the environmental characters. Most of the studies are interested with the information between the system and reservoir， to investigate their characters. For memoryless Markovian open systems， the system information losses to the environment monotonically， and the last time is relatively short. So it has many limitation for further investigation. However， in the non-Markovian case， employing the memory effect， the lost information will return to the system at a later time during the interaction. This phenomenon arouses researchers much interest， and many works related with non-Markovian dynamics have been done[8-11]recently. Between the works， Breuer et al raised a theorem called the degree of non-Markovianity which can be used to study the non-Markovian dynamics quantitatively in Ref.[12]. They calculate the changing rate of trace distance as a criterion to distinguish the states. The increment is interpreted as the return back information flow form the reservoir to the system.

However， the realistic environment is not easy to control， and it will cause decoherence. In this paper， we import a system M to simulate the environment and use the amplitude damping channel to research its characteristic. The article is organized as follows： In Sec.2， we introduce our mode and build the initial states. Then the time-dependent evolution is calculated in Sec.3. In Sec.4 we use concurrence to study entanglement evolution and the analysis is given， too. At last， we conclude the paper simply.

1 The Model

First， we introduce our model： Consider a system of two identical non-interacting two-level atoms， each of them coupled with its own reservoir which is initially in the vacuum state. Due to the independence of each atom， we only need to discuss the problem of a single atom interacting with its corresponding reservoir. The Hamiltonian of the interaction between a single atom and N-mode reservoir under the rotating-wave approximation can be written as（h =1）：

4 Conclusion

In conclusion， we have investigated the behavior of non-local decoherence in this paper. We choose the not quite perfect Bell state as the initial condition and employ a system M to consider the effect of the environment. After the amplitude damping process， we trace off the external entities to get the reduced density matrix which has the X-style. Considering the concurrence of entanglement in the Markovian and non-Markovian regime， we find that the entanglement is greatly affected by the environmental disorder. The results are identical with Ref.[14]. The work provide a method to transfer entangled communication effectively.

References：

[1]BREUER H P， PETRUCCIONE F. The theory of open quantum systems[M]. Oxford： Oxford University Press， 2007.

[2]WEISS U. Quantum dissipative systems[M]. World Scientific： Singapore Press， 2008.

[3]ZHU C W， SONG M S， HU G X， et al. Dynamic theory of die swell for entangled polymeric liquids in tube extrusions： new set of equations for the growth and ultimate extrudate swelling ratios under the free states[J]. Phys Chem， 2007，20（5）：563-581.

[4]HUANG J， ZHAN Q， LIU Z K. Ehancing the precision of parameter estimation in band gap[J]. Theor Phys， 2016，55（5）：3026-1-3026-7.

[5]MAD P， CACHEFFO A. VILLAS B C J， et al. Spontaneous recoherence of quantum states after decoherence[J]. Eur Phys J D， 2010，59（3）：487-496.

[6]VAIDMAN L， GOLDENBERG L， WIESNER S. Error prevention scheme with four particles[J]. Phys Rev A， 1996，54（3）：R1745-R1748.

[7]HE Z， ZOU J， LI L， et al. An effective method of calculating the non-Markovianity for single channel open systems[J]. Phys Rev A， 2011，83（1）：012108.

[8]REVAS A， HUELGA S F， PLENIO M B. Entanglement and non-markovianity of quantum evolutions[J]. Phys Rev Lett， 2010，105（5）：2053-2097.

[9]BREUER H P， PILLO J. Stochastic jump processes for non-Markovian quantum dynamics[J]. Europhys Lett， 2009，85（5）：50004.

[10]DING B F， WANG X Y， LIU J F， et al. Quantum discord dynamics in two different non-Markovian reservoirs[J]. Chin Phys Lett， 2011，28（10）：104216.

[11]XU G T， TONG D M. Non-Markovian effect on the classical and quantum correlations[J]. Chin Phys Lett， 2011，28（6）：060305.

[12]BREUER H P， LAINEE E M， PILLO J. Measure for the degree of non-markovian behavior of quantum processes in open systems[J]. Phys Rev Lett， 2009，103（21）： 210401.

[13]QIAN X F， EBERLY J H. Entangled states of light in classical polarization theory[J]. Optics Lett， 2010，36（20）：4110.

[14]BELLOMO B， FRANCO R L， COMPAGNO G. Non-markovian effects on the dynamics of entanglement[J]. Phys Rev Lett， 2007，99（16）：160502.

[15]COCHEANE P T. MILBURN G J， MUNRO W J. Macroscopically distinct quantum superposition states as a bosonic code for amplitude damping[J]. Phys Rev A， 1999，59（4）：2631-2634.

[16]LIN Q， LI J， GUO G C. Linear optical realization of qubit purification with quantum amplitude damping channel[J]. Chin Phys Lett， 2007，27（7）：1809-1812.

[17]WOOTTERS W K. Entanglement of formation of an arbitrary state of two qubits[J]. Phys Rev Lett， 1998， 80（10）：2245.

[18]YU T， EBERLY J H. Zero-error attacks and detection statistics in the coherent one-way protocol for quantum cryptography[J]. Quant Inf Comp， 2007，7（7）：459.9

（编辑 CXM）