斜架设对数周期天线幕成型分析

张 猛

（中国电波传播研究所，河南 新乡 453003）

斜架设对数周期天线幕成型分析

张 猛

（中国电波传播研究所，河南 新乡 453003）

文章讨论了一种实用的斜架设对数周期天线幕成型较为精确的结构分析方法。其利用理论公式对振子水平拉力和边拉索力学分析，应用MATLAB语言修正计算结果。确定各集合线分段长度、振子尾线、边拉索分段长度。方法适用于不等间距、不等大小、不同方向集中载荷作用下的斜架设对数周期天线幕成型计算。

实用；结构分析；成型计算

短波斜架设对数周期天线是驻波宽带天线，理论上可做到非常宽的带宽。本文讨论一种工程实用的结构计算方法。选取合适的坐标点，确定x，y，z坐标，初设振子垂度确定水平拉力，成型分析应用MATLAB语言修正数据，最终得到确切的值。

1 确立坐标系

一般选取高塔端两边塔地面投影连线中点为坐标原点O，x轴，y轴和z轴，如图1所示。

图1 斜架设对数周期天线计算模型坐标系示意图

2 计算振子水平拉力值

各振子在垂直投影面上均与集合线形成一角度，而集合线两端又是挂在支撑结构上，导致集合线成为振子自重的承重件之一，又天线幕对集合线是对称结构，故集合线只会在z方向存在垂度。

因为振子水平拉力的大小与振子垂度有关，故在此假设振子的垂度值来确定振子水平拉力。

为此，假定振子初设垂度数值时，综合考量振子自身的拉力要求和天线成型的外观要求，就是说所有振子的垂度相差不能太大，所以技术人员可以依据振子的初设垂度值来求的振子的水平拉力初值，进一步调整部分数值满足天线幕的成形要求，以满足天线结构技术指标。

根据前苏联著作小垂度柔索理论[1]，可知受到均布载荷并且相应支座处于不同水平面上时，此条件下振子的水平拉力值和振子的垂度值之间的公式关系如下：

式中：q是已考虑振子倾斜度的单位重量值。

式中：q1为振子上承受的均布载荷。经推导得出：

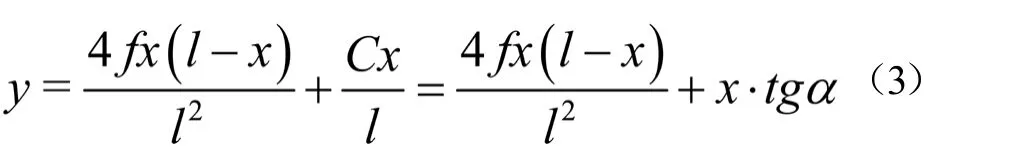
柔索长度公式为：

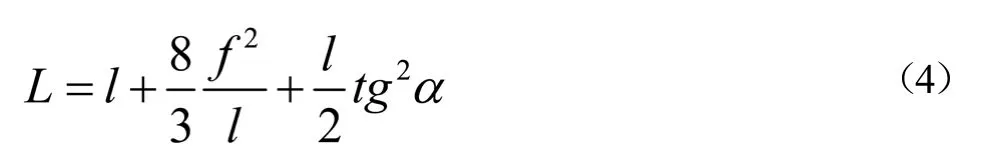
只有当α角较小值时，根据上述公式才能得出可靠的结果。当α角较大时，需要利用下面的公式得到结果。

式中：l为同一振子不同两支座挂点距离；f为假设振子的初始垂度值；H为假设振子垂度下初始值（水平张力）。

斜架对数周期天线振子上一般存在一部分外部作用的集中载荷，当数值在一定范围时，一般通过把集中载荷作用等同于均布载荷作用，这个时候公式（1）仍旧确立。不过振子均布载荷相比较与集中载荷相对较小时，不可将其等同于均布载荷，这时按振子受集中载荷作用力分析。根据小垂度柔索理论，受垂直均布载荷和集中载荷振子的方程：

设定振子上受一个集中载荷作用时的与其他因素的关系公式，假设集中载荷挂点分别距振子支点为a和b，整理并推导得出公式：

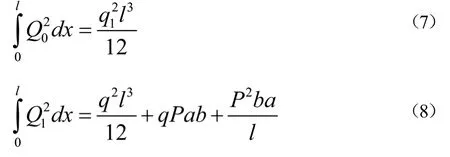
将式（1）、式（7）和式（8）代入式（6）中，推导得出：

通过公式（9）可得出振子的拉力值H1。

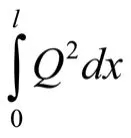
3 边拉索力学分析

在水平方向上边拉索受到振子拉力作用，可以等效于单根柔索同时受到多个集中载荷作用。采用力矩平衡原理对边拉索进行力学分析，边拉索能够将各振子支撑起来，受力均匀且成形良好。在初次计算边拉索受力时，一般根据工程实践设定一个边拉索水平拉力经验值，使用迭代法不停地用数值代入公式分析计算。首先把边拉索的水平方向作相应力学分析，以此为例边拉索上任何一单元的受力图分析如图2所示。

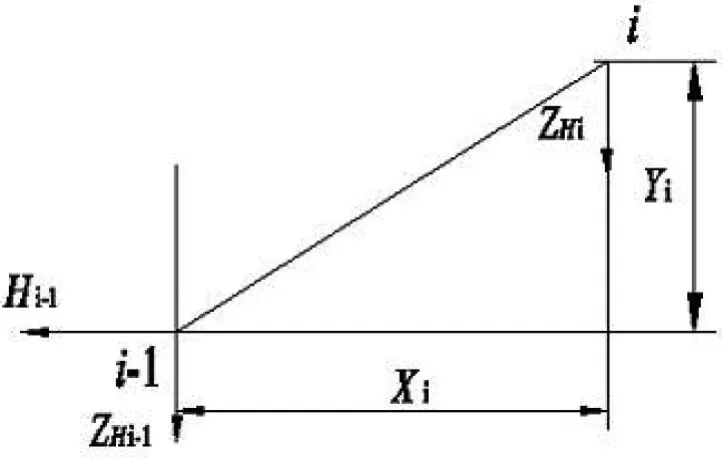
图2 边拉索上任何一单元受力分析图

依据力矩平衡关系公式得：

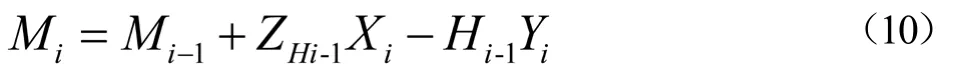
式（10）中，ZHi-1为i-1根振子拉力值，Mi-1和Mi依次为i-1点和i点的弯矩。

经变换坐标后体现在总体坐标系中，式（11）变为以下公式形式：

必须要说明的是，边拉索i-1点和i点在已确定总坐标系中的x和y坐标值是xi-1，yi-1，xi，yi。此时，可依据坐标值相互关系求解边拉索在垂直方向面上每个振子挂点处的z坐标为：

4 集合线力学分析

对数周期天线幕是沿着集合线左右完全对称的，因此天线幕两边振子对集合线的y向拉力相互抵消了，只需考虑集合线在垂直投影面的受力分析即可。结合边拉索垂直方向的受力分析。从而可得出集合线的张力和集合线上各振子挂点的z向坐标。

5 求解方法

在开始对天线幕进行分析计算前，需要先假定一组振子集合线上和边索上的挂点位置，初设边索水平拉力值、集合线水平拉力值、振子垂度值等计算所需参数。计算过程为利用计算出的振子拉力值对边拉索进行分析，边拉索分析完成后在对集合线进行力学分析，如果边拉索计算垂度值相较于初始定值偏大，计算则需要加大边拉索拉力值，反之减小值，满足初设边拉索垂度范围值时停止迭代。最终得到满足需求的数据值，从而完成全部斜架对数周期天线幕的成形分析。

6 工程实例

应用本文讨论的结构分析与计算方法，验证一斜架设对数周期天线工程实例；振子与尾线各33对；高塔标高为20 m；两侧边杆支撑高度标高为12 m，低塔标高为6 m；高塔到低塔的水平距离为62.5 m。振子与集合线俯仰夹角设为150°，振子线的单位长度重量为1.06 N/m;振子线的垂度系数为1%。利用程序计算尾线组件长度，集合线分段长度，边索坐标值及分段长度。计算仿真图如图3所示。图3—4分别为天线幕的水平投影和三维仿真图。图中上下两边①的代表边索，中间的①线代表振子线及尾线组件；天线幕中间②的代表集合线，两端②的代表端索。图4中③的代表支撑铁塔。

图3 天线幕水平投影面仿真图

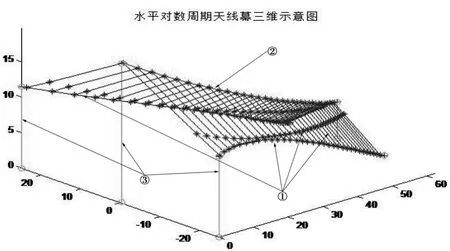
图4 天线幕三维仿真图

7 结语

本文方法适合用于不等间距、大小、方向集中载荷作用下的斜架设对数周期天线幕成型计算，应用于工程，可以保证天线成型良好。

[1]Качурин В К.小垂度柔索计算理论[M].杨福新，译.上海：科学技术出版社，1958.

[2]邵天晓.架空送电线路的电线力学计算[M].2版.北京：中国电力出版社，2003.

[3]林昌禄，聂在平.天线工程手册[M].电子工业出版社，2002.

[4]段宝岩.天线结构分析、优化与测量[M].西安：西安电子科技大学出版社，1998.

[5]JOHN D K，RONALD J M.天线[M].章文勋，译，电子工业出版社，2006.

[6]邮电部北京设计所.电信工程设计技术手册—天线和馈电线[M].北京：人民邮电出版社，1985.

[7]张其林.索和膜结构[M].上海：同济大学出版社，2002.

[8]杨庆山，姜忆南，张拉索.膜结构分析与设计[M].北京：科学出版社，2004.

[9]徐远杰，杨建东.索状柔系结构稳定平衡形状和张力计算[J].工程力学，2002（4）：75-78

[10]袁英光，张峰.基于MATLAB语言的水平对数周期天线成形分析[J].科技资讯，2015（10）：14-15.

Analysis of the log periodic antenna curtain forming with oblique erection

Zhang Meng
（China Research Institute Of Radio Waves Propagation, Xinxiang 453003, China）

This paper discusses a kind of relatively accurate and practical structure analysis method of calculation of oblique span logarithm cycle antenna screen. It uses the theoretical formula to make mechanical analysis of the horizontal tension and the side cable of the oscillator and takes advantage of MATLAB language to correct the calculation result and confirm the length of each set line, the tail of the oscillator, and the length of the side cable.The method is applicable to the calculation of the log periodic antenna screen forming of the oblique erection under the action of different distance, different size and different direction concentrated load.

practical structure; analysis; forming calculation

张猛（1986— ），男，河南永城。