基于改进西原模型的厚冲积地层基坑结构回弹参数敏感性分析
王国富,王 丹,路林海,孙捷城
(1.山东科技大学 土木工程与建筑学院,山东 青岛 266590;2.济南轨道交通集团有限公司 工程技术研究中心, 济南 250101)
基于改进西原模型的厚冲积地层基坑结构回弹参数敏感性分析
王国富1,2,王 丹2,路林海2,孙捷城2
(1.山东科技大学 土木工程与建筑学院,山东 青岛 266590;2.济南轨道交通集团有限公司 工程技术研究中心, 济南 250101)
通过在传统西原本构模型中串联Newton体,可准确追踪黄河厚冲积黏土地层中土体卸荷后的非稳定蠕变力学行为特征。以济南省文化艺术中心大厦深基坑为工程背景,采用现场监测数据分析、统计建模和FLAC3D二次开发数值模拟相结合的方法进行模型优化和改进西原方程的参数辨识,分析了围护桩的不同插入比、桩边尺寸及桩间净距3种情况下基坑卸荷导致的底板上移规律,以及立柱桩入土深度、插桩位置及桩型对基坑开挖过程中立柱桩的回弹特性的影响。结果表明:底板上移对参数的敏感程度大小为围护桩净距>插入比>桩边长;立柱桩回弹对参数的敏感程度大小为立柱桩入土深度>插桩位置>桩型。利用此规律可有效降低基坑开挖对工程桩及底板隆起的影响,确保了济南省文化艺术中心大厦深基坑的施工安全、优质,为同类地层深基坑控制立柱桩及底板隆起提供了设计经验和参考。
改进西原模型;厚冲积地层;底板隆起;立柱桩回弹;敏感性分析
1 研究背景
基坑开挖卸荷出现的大临空面在围护墙与立柱桩支撑下的水平构件组成的三维加固体系中保持平衡。立柱桩通过深入基坑设计底线,在基坑中承担水平支撑的自身重力,是三维加固体系中的重要竖向承载系统。在厚冲积黏土地层基坑工程中,三维支撑系统具有“点风险性”特征,一旦立柱桩隆起位移过大,将导致水平支撑的传力路径改变,严重时将引起三维支撑系统的破坏,引发负面社会效应[1]。现阶段,对基坑开挖过程中水平支撑体系的稳定性已有大量研究[2-3],其施工关键技术也比较成熟,但对于厚冲积黏土地层中不同支护参数下深基坑开挖卸荷导致的立柱桩及底板隆起规律的研究较少[4]。
陈锦剑等[5]利用修正剑桥模型对深基坑抗拔桩的回弹受力特性进行了分析,得到了土体卸荷引起的桩身轴力对抗拔桩的影响比轴心受压桩明显的结论;王文灿等[6]利用Drucker-Prager模型对基坑开挖导致的立柱桩隆起而引起的水平支撑体系内力的变化规律进行了分析,表明立柱桩横截面积是影响回弹的重要参数;卫凌云等[7]采用Mohr-Coulomb模型对基坑开挖中单桩及群桩的回弹规律进行了分析,发现了桩土相对刚度是影响立柱桩回弹的重要因素;Iwasaki等[8]早期发现了基坑开挖对工程桩造成的回弹影响的现象,并借助理论分析手段对回弹的影响范围进行了估算;Poulos等[9]在早期同样借助理论方法,以自设条件研究了膨胀土回弹对立柱桩的影响。可见,分析基坑回弹的手段多种多样,但每一种模型都有各自的使用特点和局限性,很难将单一模型推广到其他工程当中。
济南地质条件为黄河厚冲积平原,各层岩土体具有极其复杂的力学行为,具有显著的蠕变特性并伴随较高的触变特性。目前,对于济南特殊黄河厚冲积黏土地质条件下数值本构模型的研究,各学者之间并没有达成统一的观点[10-11]。
本文以济南省文化艺术中心大厦深基坑为工程背景,采用有限差分法数值模拟软件结合改进的西原本构模型,利用围护桩及立柱桩各自参数为条件因子,研究各因子下基坑底板及立柱桩的隆起规律及敏感程度,并结合现场实测数据对最佳支护参数进行了验证,对于指导工程施工、保证施工的优质、高效具有重要意义。
2 西原模型改进
传统的西原模型可描述黏土地层中土体单元加载或卸载时的瞬时弹性变形及蠕变变形,但对于追踪后期的非稳定蠕变特性却不太理想。Newton体在发生位移时有一个时间过程,需要消耗一定的时间才达到最终的变形状态,与厚冲积黏土地层土体单元卸载后的蠕变特性较为符合,并且牛顿体的黏滞系数(单位MPa/d)可表征某一时间段内发生相对变形时抵抗变形的能力,具有明显的时间特性。因此通过在改进的西原模型中串联一个Newton体,可准确追踪厚冲积黏土地层下基坑开挖卸荷时的蠕变特征。
2.1 西原本构方程推导
西原本构方程及串联牛顿体的改进西原模型如图1所示。
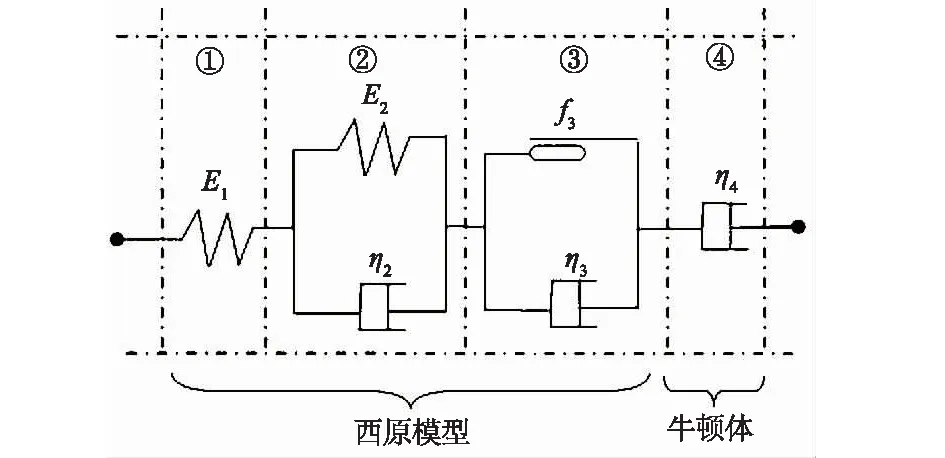
图1 改进西原模型Fig.1 Nishihara model improved with Newton fluid
西原本构方程及蠕变方程推导过程如下。
根据静力平衡条件有
(1)
式中:σ1,σ2,,σ3分别为元件①,②,③的应力;σNis是西原模型的总应力。
由变形协调条件知
(2)
式中:ε1,ε2,ε3分别为元件①,②,③的位移;εNis是西原模型的总位移。
已知元件①本构关系为
(3)
元件②本构关系为
(4)
元件③本构关系为
(5)
式中:E1,E2分别为元件①,②中胡克体的弹性模量;σf为相对应的应力;η2,η3分别为元件②,③中牛顿体的黏滞系数;f3为元件③圣维南体的抗拉强度;σf为③对应的应力。
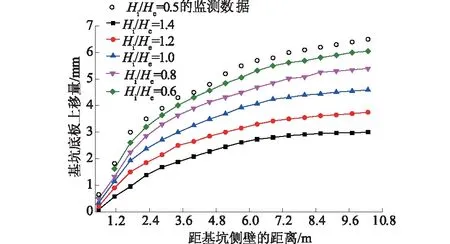
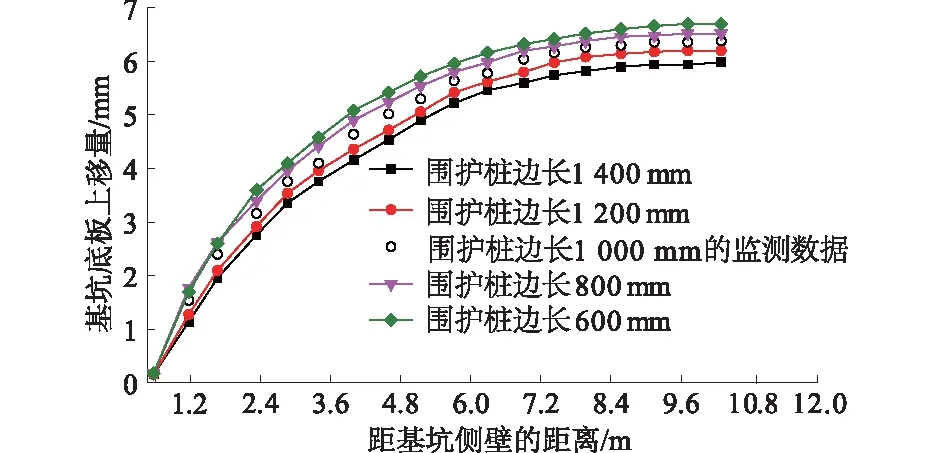
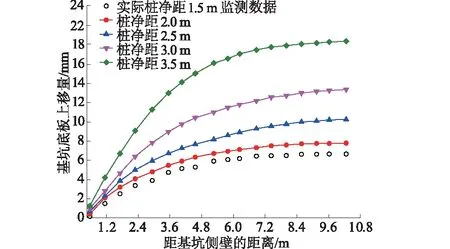
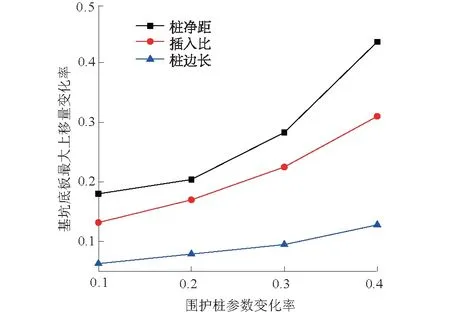
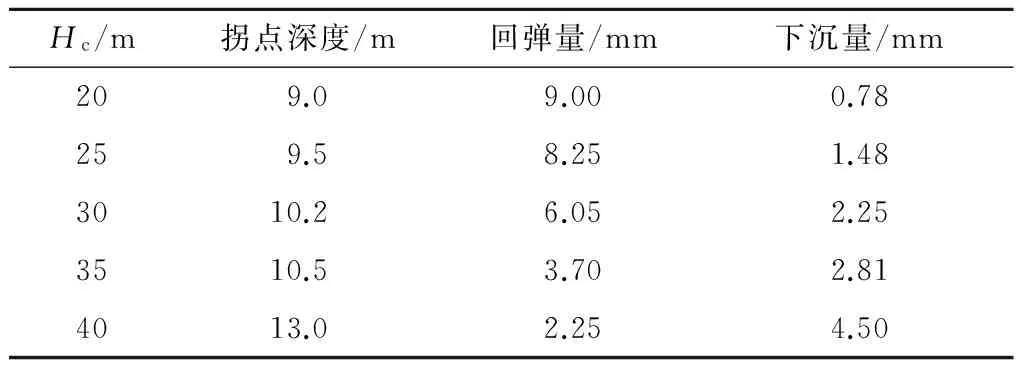
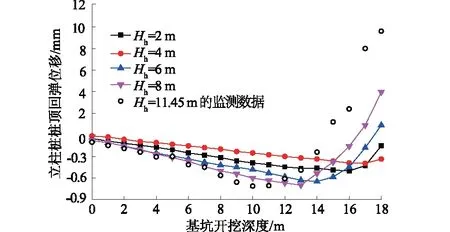
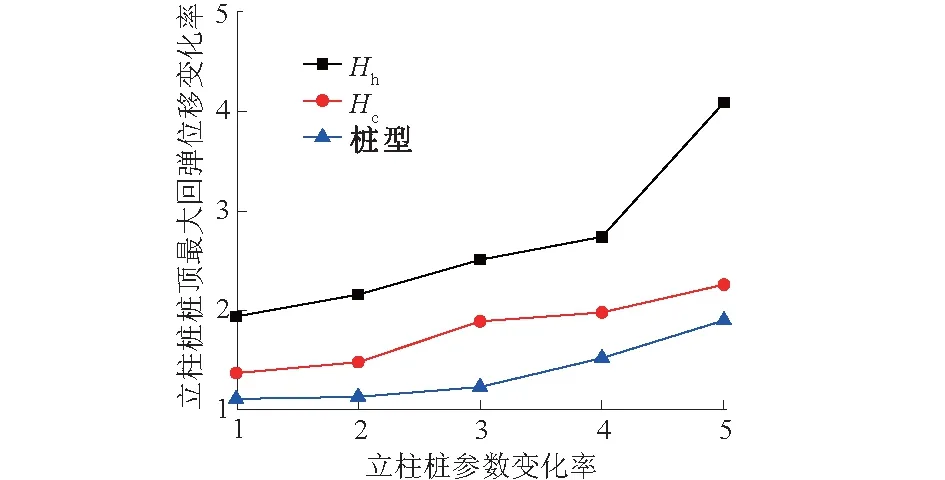
2.1.1 当σf 当σf (6) 则 (7) 对式(3)两边同时求导得 (8) 将式(3)、式(4)、式(7)、式(8)代入式(6)中得 (9) 整理得出此条件下的西原本构模型为 (10) 式中η4为元件④中牛顿体的黏滞系数。 2.1.2 当σf≥f3时的西原本构模型 当σf≥f3时,有 (11) 根据变形叠加原理知 (12) 对式(8)两边再求导得 (13) 根据串联元件应力相等的原理知: (14) (15) 其中: (16) 将式(8)、式(10)和式(12)—式(15)代入式(11)中整理得出此条件下的西原本构方程为 (17) 综上可得,此条件下西原本构模型为 (18) 2.2 西原蠕变本构模型推导 根据串联模型总应变等于各部件应变之和定律,设应力为常量(σNis=σ0=C)。则: 元件①蠕变方程为 (19) 元件②蠕变方程为 (20) 元件③蠕变方程为 (21) 综上可得,西原模型的蠕变方程为 (22) 2.3 西原卸载弹性后效及黏性流动方程推导 设经历加载时间t1时的应力为σC,然后进行卸载(σ=0),经历时间t之后,各元件应变量如下所述。 元件①应变瞬时恢复,即 (23) 元件②因黏壶的存在,其应变为 (24) 元件③应变为 (25) 则西原模型卸载弹性后效及黏性流动方程为 (26) 2.4 改进的西原本构方程推导 静力平衡条件为 (27) 式中:σ为改进西原模型的总应力;σ4为元件④的应力。 变形协调条件为 (28) 式中:ε为改进西原模型的总应变;ε4为元件④的应变。 元件④本构关系为 (29) (30) (31) 2.4.1 当σf 对西原本构模型两边求1次导得 (32) 将式(30)、式(32)代入式(31)中得 (33) 其中: (34) 将式(34)代入式(33)中得 (35) 整理此条件下的改进西原本构方程为 (36) 2.4.2 当σf≥f3时的改进西原本构模型 当σf≥f3时,此时西原本构方程为 (37) 将式(29)、式(37)代入式(32)中,整理得出此条件下的本构方程为 (38) 2.5 改进西原模型蠕变方程推导 根据串联模型总应变等于部件分应变之和定律,设应力为常量(σNis=σ4=σ0=C),则元件④蠕变方程为 (39) 由串联模型总应变等于部件应变之和的定律,联合西原蠕变方程式(22)与式(40)得七元件蠕变方程为 (40) 2.6 改进西原模型卸载弹性后效及黏性流动方程推导 设经历加载时间为t1时应力为σC,然后进行卸载(σ=0),经历时间t之后,元件④卸载方程为 (41) 根据串联模型总应变等于部件分应变之和定律,则七元件卸载弹性后效及黏性流动方程为 (42) 通过可以利用内嵌FISH语言实现编程功能的快速拉格朗日有限差分法计算软件FLAC3D,将上文研究得出的改进西原本构方程、蠕变方程通过生成DLL(动态链接库),嵌入至软件中,实现对软件的二次开发[12],并将改进西原模型程序化。以济南省文化艺术中心大厦深基坑为工程背景建立三维数值模型,通过分析不同支护参数下立柱桩及底板隆起的规律,得出最佳安全支护参数,并结合实测数据对改进的西原本构模型进行评价。 3.1 工程概况 省会文化中心项目位于济南西部新城核心区中心发展轴与腊山河景观带的交汇处,是由大剧院、中心广场、配套高层3部分组成的大型城市综合体,总建筑面积约38万m3。拟建场地为拆迁场地及原耕地,周边环境简单,无地下管线和既有建(构)筑物。基坑设计尺寸为:长×宽×深=501.71 m×22.9 m×18.4 m,采用桩锚联合水平钢支撑的支护结构形式,如图2所示,D为基坑开挖宽度的1/2,B为基坑顶部尺寸,He为基坑开挖深度,Hi为围护桩插入基坑下部土体的长度,Hc为立柱桩插入基坑底部的长度。根据基坑设计文件,确定围护桩为边长为1 m的方桩,间距为1.5 m,He=18.4 m,Hi=9.2 m;立柱桩为边长1.5 m的方桩,在基坑中间位置布设一排,间距为3 m,Hc=20 m,Hh=11.45 m。 图2 基坑支护结构示意图Fig.2 Schematic drawing of foundation pit support structure 3.2 数值模型建立 根据对称性,现取基坑平面的1/4建立数值模型[13-14],模型尺寸为长×宽×高=100 m×100 m×100 m,模型总计155 000个单元,452 000个节点,如图3所示。模型上边界为自由面,外侧边界为水平链杆约束,中心施加对称约束,底面为固定约束。在模拟中,围护桩及立柱桩均采用实体单元,并在桩周设置接触面,实现桩、土之间的相对滑移。按设计分别在基坑开挖深度的1.5,7.9,14.3 m处设置水平支撑及预应力锚索,根据刚度等效理论将水平支撑简化为壳单元。 图3 3D数值模型 图4 围护桩实测与模拟水平位移比较Fig.4 Comparison of horizontal displacement of pile between simulation and field test of support piles 3.3 模型有效性验证及参数确定 考虑到桩与土之间不存在抗拉强度,因此选取接触面的抗拉强度为0,切向刚度取值参考FLAC手册,其余参数则参考文献[15]。岩土体依据勘察资料将模型概化为7层,并依据文献[16]确定模型的初始参数。围护桩的变形能准确反映岩土体数值参数与结构单元参数的合理性,通过MATLAB对数值模拟得到的围护桩水平位移数据与现场实际测量得到的围护桩水平位移数据进行二次回归非线性拟合,同时对模型各参数进行微调,当实测数据与模拟数据两者的逼近率在0.90以上时,便认为参数调整到位。 根据实测结果与计算结果,绘制桩体水平位移随深度变化的曲线如图4所示。桩体水平位移计算值与实测值随深度变化曲线均为“中凸形”,最大水平位移实测值为7.75 mm,仅比最大水平位移模拟值8.42 mm小了0.67 mm,这是由于现场机械作业及人员走动等各种动荷载增加了支护结构荷载。但基坑模 拟与实测曲线变化趋势大体一致、差值微小,表明数值模型及改进西原模型的选取是合理的,可以为施工、设计等提供可靠依据,以此确定的参数见表1。 表1 改进西原模型关键参数 注:γ为土层重度;E1,E2为元件①,②中弹簧体的弹性模量;η2,η3,η4为元件②,③,④中Newton体的黏滞系数;f3为元件③的抗拉强度。 4.1 敏感性定义 参数敏感性曲线能分析不同参数对参照标准特征影响的剧烈效果,若曲线计算值越大,说明参数对参照标准的影响愈剧烈。 4.2 基坑底板隆起参数敏感性分析 4.2.1 围护桩插入比对底板隆起的贡献 如图5所示,为基坑开挖完成后沿基坑宽度方向底板的隆起位移随着围护桩插入比变化的曲线图(其他支护参数不变)。围护桩在基坑开挖的过程中起到遮帘的作用,切断因土体卸荷在坑底与坑壁造成的压力差值而出现的土体滑移,限制坑底土体隆起;在基坑底板设计面以下的围护桩,在桩身与土体接触处存在侧摩阻力,当Hi长度超过土体回弹的中性点时,围护桩会限制周围土体的回弹,并且黏土地层的蠕变特性,使得基坑土体在开挖完成后仍然出现一定的隆起。 图5 不同围护桩插入比的底板上移曲线Fig.5 Curves of upward displacement of floor vs.ratios of support pile depth in soil to excavation depth 基坑实际插入比为Hi/He=0.5,在此条件下的基坑底板隆起规律如图5所示。为了研究不同插入比下的基坑底板隆起规律,分别模拟插入比为0.6,0.8,1.0,1.2,1.4这5种情况下的底板隆起特征。当围护桩Hi/He为0.5时,基坑底板回弹及隆起位移最大,越接近基坑中心位置,位移发展速度越快,最大隆起值为6 mm;当Hi/He为1.4时,基坑中心位置最大上移量为2.8 mm,上移量降幅明显。由5组曲线变化规律看出,随着插入比的增加,基坑底板各点上移量接近等幅下降。 4.2.2 围护桩边长对底板隆起的贡献 图6为沿基坑宽度方向底板隆起量随着围护桩边长尺寸变化的规律(其他支护参数不变)。5组曲线趋势及形状接近,差异较小,预制桩边长分别为600 mm及1 400 mm时,基坑中心土体最大上移量为6.00 mm和6.75 mm。增加桩边尺寸会增大桩土之间的侧摩阻力,在插入比及桩净距不变时,增加的侧摩阻力只能在一定程度上限制邻近土体的回弹,但对于远处土体的上移限制效果较差。 图6 不同围护桩边长时的底板上移曲线Fig.6 Curves of upward dispacement of floor vs. side length of support piles 4.2.3 围护桩间距对底板隆起的贡献 如图7所示,为基坑底板回弹位移随着围护桩净距变化的规律。在桩插入比及桩边尺寸一定时,若相邻桩净距较小,基坑两侧土体因卸荷产生的内外压力差而形成的应力传递路径被围护桩形成的拱效应隔断,可有效限制坑底隆起;当围护桩净距较大时,土拱效应无法形成[18-19],基坑外部的侧压力透过围护桩传递至基坑底板,导致底板隆起和回弹。 图7 不同围护桩间距时的底板上移曲线Fig.7 Curves of upward dispacement of floor vs. spacing of support piles 5组数据在形状上相似,沿基坑宽度方向上在距离基坑中心较近时,回弹及隆起位移逐渐加大。在围护桩净距为1.5 m时,基坑最大上移量为3 mm,但当净距增加至3.5 m时,最大总上移量增加9.1 mm,且上移速率增加较快。5组曲线中,围护桩净距按照0.5 m的间距增加,而最大上移增加量却为0.5,1.0,1.5,2.0 mm,增幅逐渐增大。 4.2.4 围护桩参数敏感性分析 图8 底板最大上移量随围护桩参数变化率曲线Fig.8 Maximum upward displacement of floor vs. change rate of support pile parameters 4.3 立柱桩回弹参数敏感性分析 立柱桩在基坑三维支撑系统中是维持水平稳定的重要结构,若立柱桩出现回弹,会导致水平支撑结构出现反向变形,衍生较大的附加应力。基坑土体回弹及隆起在深度方向上存在一个中性点,在中性点以下的围护桩,由于土体未受到扰动,弹性模量及黏滞系数等参数未发生改变,从而施加至桩身的摩阻力相对较大;而中性点以上的土体,由于土体卸荷导致坑底上移,在上移的过程中,土体有膨胀松散的趋势,导致弹性模量变小、黏滞系数变小,导致作用在围护桩上的侧压力出现减少。立柱桩入土深度较浅时,基坑底部土体扰动范围较深,扰动深度甚至超过了立柱桩入土深度,导致基坑土体上移时,会携裹着立柱桩一起回弹。 4.3.1 立柱桩入土深度 如图9所示,为基坑中心位置处(Hh=11.45 m)立柱桩回弹位移量在不同Hc情况下随基坑开挖深度的变化曲线。实际开挖中,围护桩回弹量是最大的,并且模拟结果与实测结果在趋势上保持一致,即5种情况下立柱桩均在基坑开挖的初期发生沉降,直至开挖到一定深度时,才出现回弹。 由表2可知,立柱桩Hc越大,桩顶出现回弹时对应的基坑开挖深度越深,并且在回弹之前桩顶下沉量也较大,伴随的下沉速率较高;Hc越大,立柱桩桩顶总回弹位移越小。 表2 不同Hc下立柱桩上移特征 4.3.2 立柱桩位置 图10为立柱桩桩长一定时(Hc=40 m),在Hh不同情况下,立柱桩桩顶回弹量随基坑开挖深度变化曲线。由曲线可以看出,在Hh=2 m时,立柱桩在整个基坑开挖期间几乎不出现上移,随着Hh的逐渐增大,曲线出现拐点的时间越早,下沉量与回弹量均越大。 图10 不同立柱桩位置的立柱桩回弹位移Fig.10 Curves of rebound displacement of column piles at different positions 如表3所示,立柱桩距离基坑中心点越近,曲线出现拐点的时间越早,下沉量与回弹量均越大。黏性土具有较强触变性,基坑中间位置的土体卸荷程度最大,从而对土体的扰动最为剧烈。且回弹规律与图5—图7中底板上移规律密切联系,说明立柱桩的位置对自身上移量起到了关键作用。 表3 不同Hh下立柱桩上移特征 4.3.3 立柱桩桩型 在基坑中心位置处(Hh=11.45 m,Hc=20 m),且桩相同横截面积下,分析桩形状分别为方桩、圆桩、十字形桩、扩底桩、挤扩支盘桩5种桩型的回弹量。因扩底桩底端具有较大的固定力,并且中性点以上土体回弹对扩底桩产生的上拔力较小,从而桩体回弹量较小;而十字型桩具有较大的侧面积,在相同的侧摩擦系数下,中性点以下土体侧压力大于中性点以上土体部分的侧压力,限制了桩身上移量;上移量位居中间的是挤扩支盘桩,因中性点上部土体回弹时产生较大的上拔力,带动桩身上移。根据模拟计算结果,得出立柱桩总上移量由大到小分别为:圆桩、方桩、十字形桩、挤支扩盘桩和扩底桩。 4.3.4 立柱桩参数敏感性分析 同样将立柱桩不同参数下的模拟计算结果进行无量纲化,作立柱桩自身回弹的敏感性曲线,如图11所示。可得立柱桩各参数对自身桩顶回弹较为敏感的排序依次为:Hh>Hc>桩型。 图11 立柱桩桩顶最大回弹位移变化率随立柱桩参数变化率曲线Fig.11 Change rate of maximum rebound displacement of pile top vs. change rate of column pile parameters 本文研究了改进西原本构模型的特点,推导了其本构方程及蠕变方程,并通过C++语言实现了对FLAC3D的二次开发,将研究的新本构方程程序化。以济南深基坑为工程背景研究了围护桩参数、立柱桩参数对基坑底板及立柱桩回弹的敏感程度。得到以下结论: (1) 改进的西原模型通过串联Newton体不仅可以描述黏土地层中土体单元加载或卸载时的瞬时弹性变形及蠕变变形,而且可准确追踪后期的非稳定蠕变特征,与济南黄河厚冲积黏土地层土体变形特点较为符合。 (2) 围护桩的参数对底板上移起到重要作用。在基坑中心位置处的土体上移量最大,并且在围护桩净距较小及插入比较大时,能有效限制基坑底板上移。当插入比为1.0时,底板最大隆起量仅为4 mm,且决定基坑底板上移的参数其敏感程度大小为:桩净距>插入比(Hi/He)>桩边长。 (3) 在围护桩参数确定的情况下,立柱桩自身参数决定了其回弹位移量。立柱桩回弹与基坑底板上移有密切联系,但改变立柱桩的参数可有效降低其回弹位移量。当立柱桩与坑壁相距2 m时,立柱桩回弹量仅为0.38 mm,且决定立柱桩回弹的参数其敏感程度大小为:立柱桩位置(Hh)>立柱桩入土深度(Hc)>立柱桩桩型。 [1] 若 枫,马 郧,徐光黎,等.基坑被动区阶梯式加固尺寸对桩位移影响分析[J]. 长江科学院院报,2013,30(7):86-90,100. [2] 李方成,郭利娜,胡 斌,等.基于MIDAS软件探讨施工工序对深基坑稳定性的影响[J]. 长江科学院院报,2013,3(3):49-55. [3] 陈 明,李镜培. 砂土地基中开挖过程对立柱桩的影响分析[J]. 力学与实践,2014,36(1):59-63. [4] 贺 翀. 深基坑的立柱桩隆起计算[J].岩土工程学报,2010,32(增1):74-78. [5] 陈锦剑,王建华,范 巍,等.抗拔桩在大面积深开挖过程中的受力特性分析[J].岩土工程学报,2009,31(3):402-407. [6] 王文灿,刘 琦,仲晓梅.超深基坑立柱竖向位移及其对水平结构的影响数值模拟[J].建筑结构,2011,41(增刊):1344-1349. [7] 卫凌云,秦胜伍,陈慧娥.基坑开挖对单桩及群桩回弹位移的影响分析[J].吉林大学学报(地球科学版),2014,44(2):584-590. [8]IWASAKI Y, WTNABE H, FUKUDA M,etal. Construction Contrl for Underpinnig Piles and Their Behaviour Duing Excavation[J]. Geotechnique,1994,44(4):681-689. [9]POULOS H G, DAVIE E H. Pile Foundation Analysis and Design[M]. New York: Wiley, 1980. [10]代春泉,秦 哲,苏建光.黄河冲积平原深基坑施工变形黏弹塑性分析[J].岩土力学,2013,34(增1):142-147. [11]徐 飞,王渭明,张乾青,等.黄河冲积平原地区超大型深基坑开挖现场监测分析[J].岩土工程学报,2014,36(增2):471-478. [12]代春泉,王 磊,王渭明.基于各向异性本构模型的隧道支护控制[J].北京工业大学学报,2012,38(8):1202-1207. [13]梁发云,褚 峰,宋 著,等.深基坑变形特性的离心模型试验、数值计算与现场实测对比分析[J].长江科学院院报,2012,29(1):74-78. [14]连宝琴,胡 斌,王新刚,等.武汉地铁名都车站基坑开挖监测与数值分析[J].长江科学院院报,2014,31(5):34-38. [15]王孝兵,文松霖,徐文强.大直径长桩接触面参数的敏感性分析[J]. 长江科学院院报,2011,28(2):38-44,55. [16]宋德彰,孙 钧.岩质材料非线性流变属性及其力学模型[J]. 同济大学学报, 1991,19(4): 395-401. [17]徐 伟,李靖祺,段朝静.某特殊平面形状深基坑围护结构对土层参数敏感性分析[J].岩土工程学报,2010,32(增1):173-176. [18]贾海莉,王成华,李江洪.基于土拱效应的抗滑桩与护壁桩的桩间距分析[J]. 工程地质学报, 2004, 12(1):98-103. [19]杨有海,武进广.杭州地铁秋涛路车站深基坑支护结构性状分析[J]. 岩石力学与工程学报,2008, 27(增2):3386-3392. (编辑:姜小兰) Sensitivity Analysis of Foundation Pit Rebound in Thick Alluvial ClayBased on Improved Nishihara Model WANG Guo-fu1,2, WANG Dan2, LU Lin-hai2, SUN Jie-cheng2 (1.College of Civil Engineering & Architecture, Shandong University of Science and Technology, Qingdao 266590 ,China; 2.Engineering and Technology Research Center, Jinan Rail Transit Group Co. Ltd., Jinan 250101, China) The upward displacement of pile and floor is a damage for the balance of support system during the excavation foundation of pit in thick alluvial clay Nishihara model improved with Newton fluid could well describe the behavior of creep deformation during pit excavation,and also trace the behavior of interface between pile and soil.The regularities of upward displacement of floor in the presence of different ratios of inserted pile depth to excavation depth,side lengths and spacings of support pile,as well as the rebound of column pile in the presence of different depths in soil,positions and types of column pile were analyzed via field data,improved Nishihara model and secondary development of FLAC3D.The deep foundation pit of Culture Center of Jinan Province was taken as an engineering background.Results revealed that the sensitivity of the upward displacement of pit floor to different factors follows the order of:distance of adjacent support pile>ratio of inserted depth to excavation depth>length of support pile; and the sensitivity of the rebound of column pile follows the order of depth of column pile in soil>position of pile>shape of plie. The results could be a guidance for reducing the influence of excavation on the upward displacement of pile and floor. improved Nishihara model;thick aluvial;rebound of foundation pit;column pile rebound;sensitivity analysis 2015-11-05; 2015-11-26 山东省自然科学基金项目(ZR2014EEM029,ZR2014EEQ028);山东省重点研发项目(2015GSF120017);住房城乡建设部2015年科学技术项目计划-研究开发项目(2015-K5-004);山东省住房和城乡建设厅科学技术计划项目(KY053) 王国富(1964-),男,山东威海人,研究员,博士,主要从事岩土工程、结构工程相关理论与技术的研究工作,(电话)0531-58908128(电子信箱)metro_jinan@126.com。 王 丹(1990-),男,山东聊城人,助理工程师,硕士,主要从事基坑工程、隧道工程方面的研究,(电话)15169161080(电子信箱)492020719@qq.com。 10.11988/ckyyb.20150941 2016,33(10):84-92 TU43 A 1001-5485(2016)10-0084-09
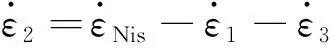
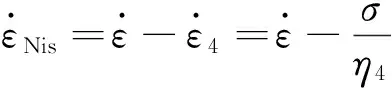
3 工程应用
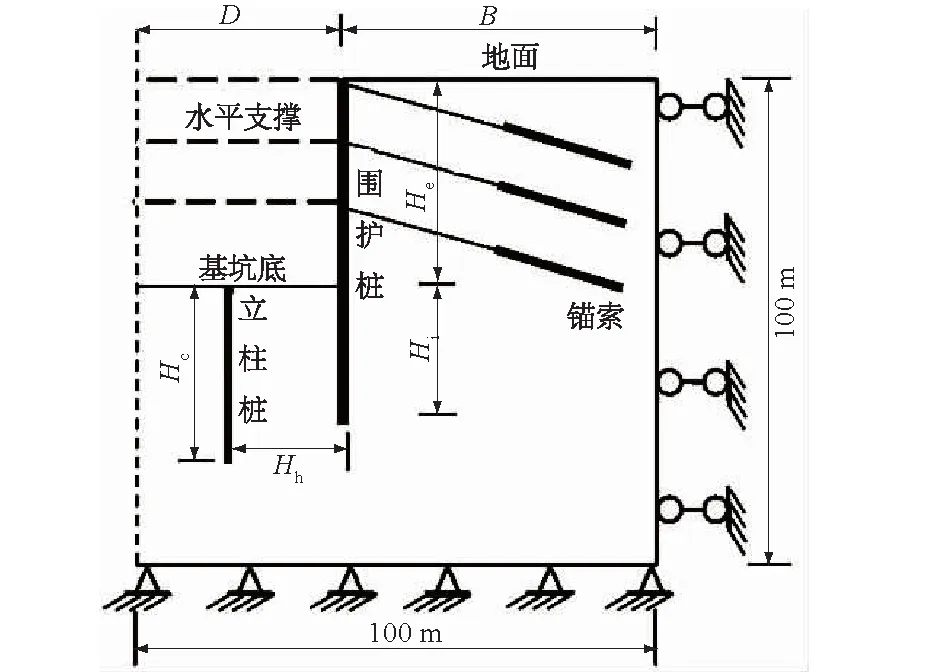
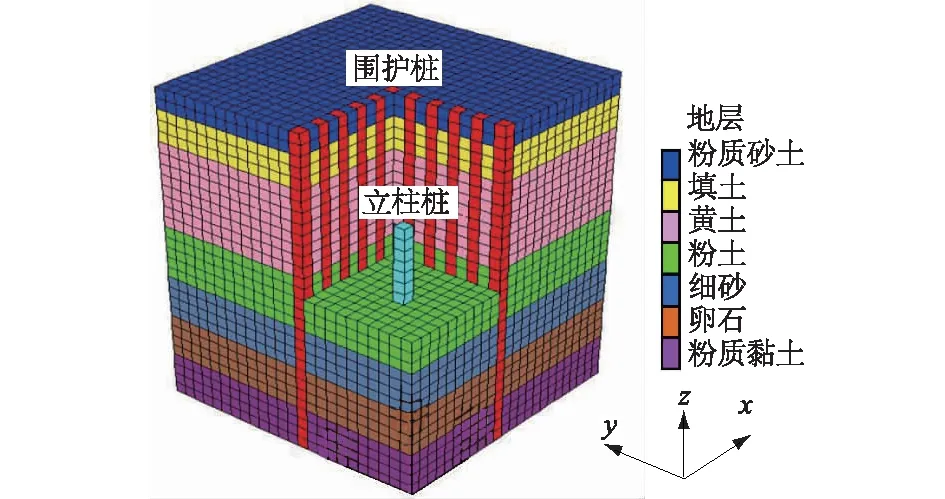
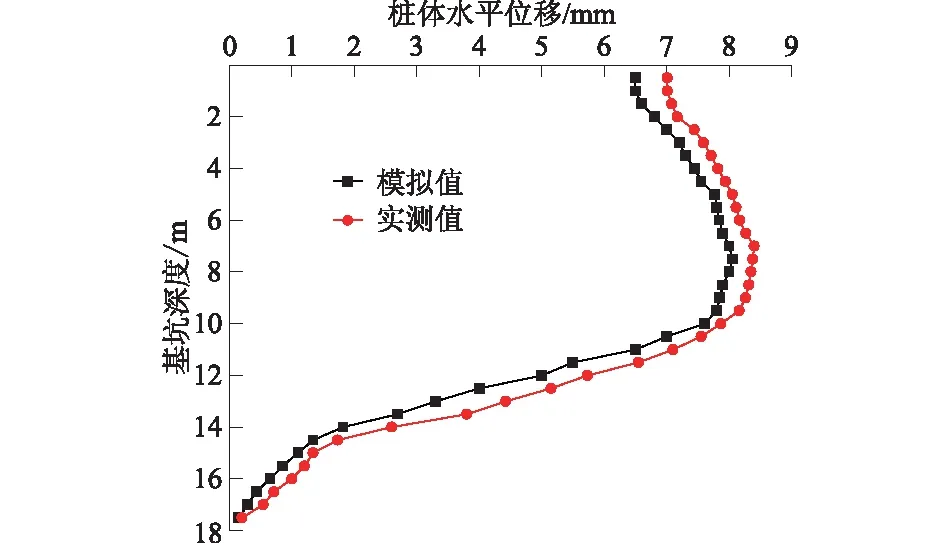
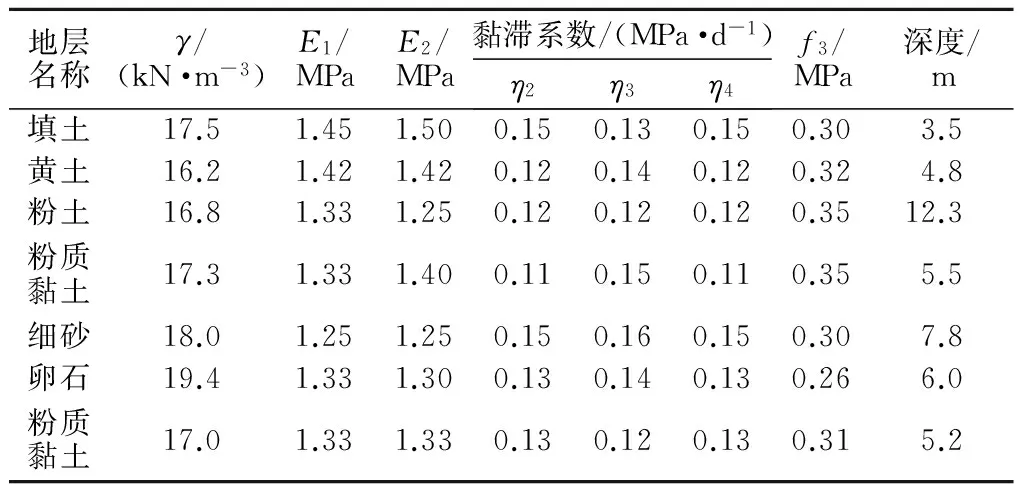
4 结构回弹支护参数敏感性分析

5 结 论

