基于SSO-PP模型的滇池流域水质综合评价

吴光琼, 方金鑫

(云南省水文水资源局 丽江分局，云南 丽江 674100)



基于SSO-PP模型的滇池流域水质综合评价

吴光琼, 方金鑫

(云南省水文水资源局 丽江分局，云南 丽江 674100)

水质评价；投影寻踪；群居蜘蛛优化算法；群体智能；滇池流域

1 研究背景

2 SSO-PP水质评价模型

2.1 群居蜘蛛优化算法

群居蜘蛛(Social Spider)是一类倾向群居的蜘蛛物种，个体间保持有复杂的协作行为准则，根据雌雄执行多种任务，如捕食、交配、蜘蛛网设计及群体协作等。群居蜘蛛由个体和蜘蛛网络组成，个体分为雄性和雌性2种类别。种群依据个体雌雄分配不同的任务，个体之间通过直接或间接的协作将有用信息通过蜘蛛网络传递给群居中的其他个体，并将此信息编码成振动的强弱在个体间进行协作。振动的强弱可被群居中个体解码成不同的信息，如猎物的大小，相邻个体特征等，而振动的强度取决于蜘蛛的重量和距离。SSO算法在真实模拟群居蜘蛛群体内不同协作行为的基础上，引入新的计算机制，有效避免了目前常规群算法中存在的早熟收敛和局部极值问题[19]。在解决连续变量优化问题时，SSO算法是以迭代的方式不断地寻找最优值，最重个体蜘蛛所处的位置即优化问题的解。

假设整个搜索空间为蜘蛛网络，每个潜在解即为搜索空间中蜘蛛所处的位置。依据雄性和雌性的搜索机制，每个个体分属于2种不同的进化算子，并在群体内模仿不同的协作行为。参考文献[19]中SSO算法步骤可归纳如下。

步骤1：设搜索空间的维度n，雌性蜘蛛Nf，雄性蜘蛛Nm以及总种群数量N。定义Nf及Nm分别为

Nf=floor[(0.9-rand0.25)N] ；

(1)

(2)

式中：rand为[0,1]上的随机数；floor(·)为实数到整数的映射。

步骤2：设种群S由N个蜘蛛个体组成，N由2个子群的F和M组成。随机初始化雌性蜘蛛(F={f1,f2,…，fNf})和雄性蜘蛛(M={m1,m2,…,mNm})，则S={s1=f1,s2=f2,…,sNf=fNf,sNf+1=m1,sNf+2=m2,…,sN=mNm}，定义交配半径r为

(3)

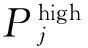
步骤3：计算每一个蜘蛛的重量wi，即

(4)

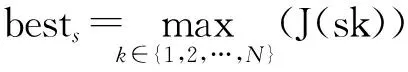
步骤4：根据协作机制按式(5)移动雌性蜘蛛，即

(5)

式中:α，β，δ及rand均为[0,1]上的随机数；k为当前迭代次数；sc，sb分别为最近个体i的较好重量和最佳重量；振动因子Vibci，Vibbi分别由式(6)、式(7)表示，即

(6)

(7)

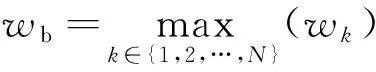
步骤5： 根据协作机制按式(8)移动雄性蜘蛛，即

(8)

式中：sf为最近雌蜘蛛个体重量；振动因子Vibfi可由式(9)表示，即

(9)

式中wf为常量。

步骤6： 在交配过程中，以每个个体重量定义交配概率，越重的蜘蛛个体获得繁育后代的概率越大。本文按轮盘赌法确定概率psi，即

(10)

步骤7：判断是否满足停止条件，若满足则算法结束；否则，返回步骤3。

2.2 投影寻踪模型简介

PP模型用于水质综合评价简要算法可归纳如下[10-11]。

(11)

式中：x(i,j)为第i组第j个评估指标值；xmax(j)，xmin(j)分别为评估数据集中第j个评估指标的最大、最小值；n，m分别为数据集数量及评估指标数目。

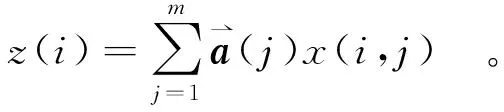
(12)

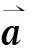
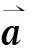
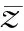
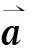
步骤5：评价。同理计算得到各年度投影值z(i)，依据z′(k)对各断面年度水质进行综合评价。

2.3 SSO-PP模型实现步骤

SSO-PP水质综合评价模型计算步骤可归纳如下。

步骤1：数据预处理。利用式(11)对水质评价数据进行归一化处理。

步骤2：确定SSO算法适应度函数。由于SSO算法是求解极小值，因此将式(13)的倒数作为目标函数，即以式(14)作为适应度函数

(14)

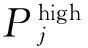
步骤4：SSO算法寻优操作。按上述SSO算法进行最优个体寻优，直至满足算法迭代终止条件。

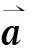
步骤6：构造水质评价分级标准z′(k)，计算各年度投影值z(i)，依据z′(k)对各断面年度水质进行综合评价。

3 应用实例

3.1 数据来源

滇池位于昆明市区西南面，是云贵高原水面最大的天然淡水湖泊，横亘东西的海埂湖堤将滇池分割为南北2个水域，北面为草海，水域面积约11 km2；南面为滇池外海，水域面积298 km2，占滇池总面积96.4%。滇池流域是云南省政治经济文化中心，人口稠密，经济发达，流域内河流众多，水系发育，多年平均水资源量5.7亿m3。自20世纪80年代以来，滇池出现湖泊富营养化的典型特征，蓝藻、水葫芦大量繁殖，致水质恶化，蓝藻暴发不断加剧，成为国家重点治理的“三湖”之一。本文选取对水体影响较大的NH3-N,TN,CODMn,BOD5和TP作为水质综合评价因子，并利用PP模型对2003—2013年滇池流域1#—4#4个断面的水质进行综合评价。水质数据及分级标准见表1、表2。

3.2 样本生成及参数设置

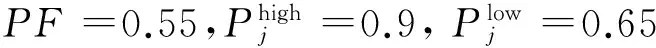
3.3 构造水质评价分级标准

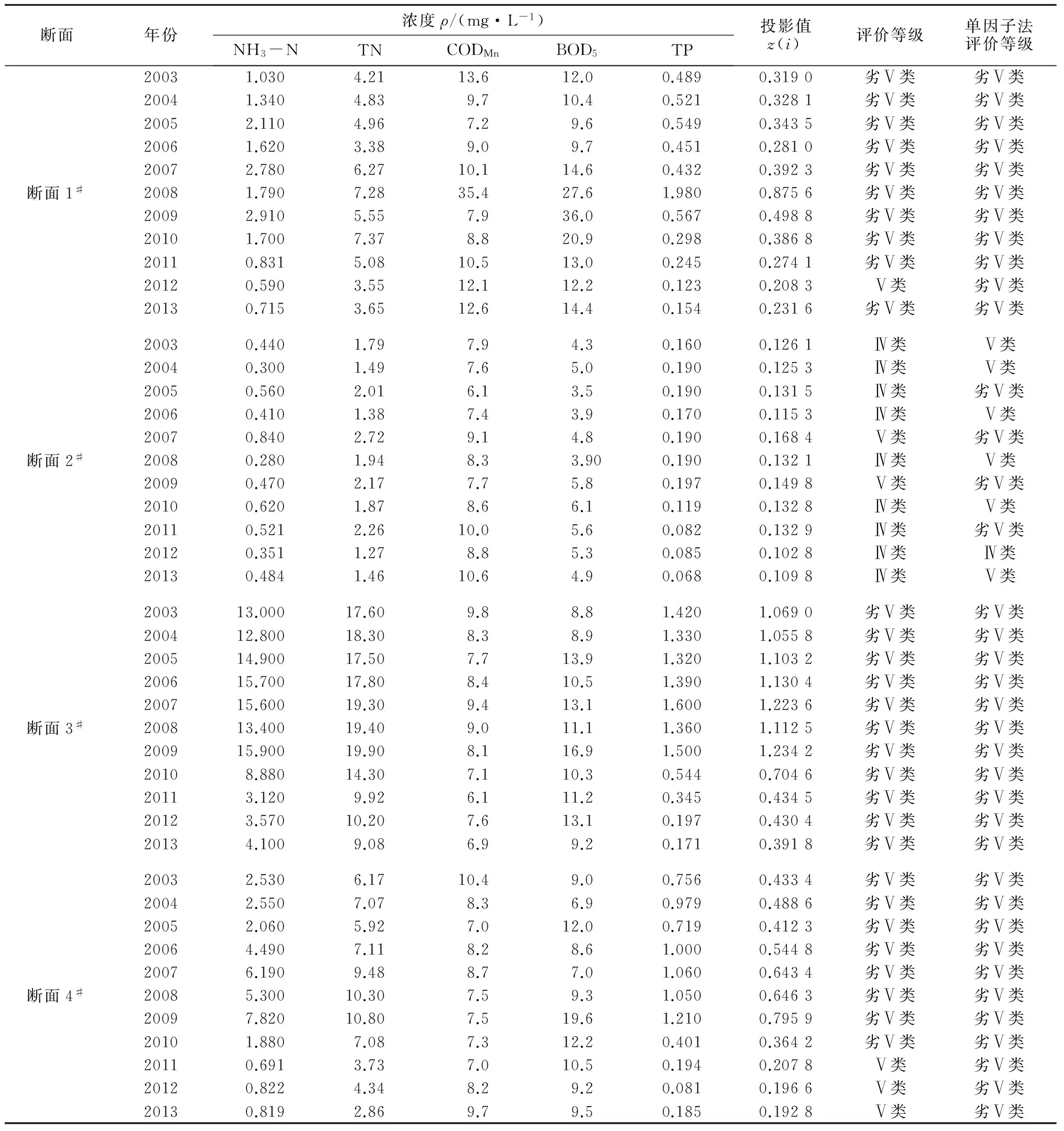
表1 2003—2013年各断面5项水质评价因子监测值

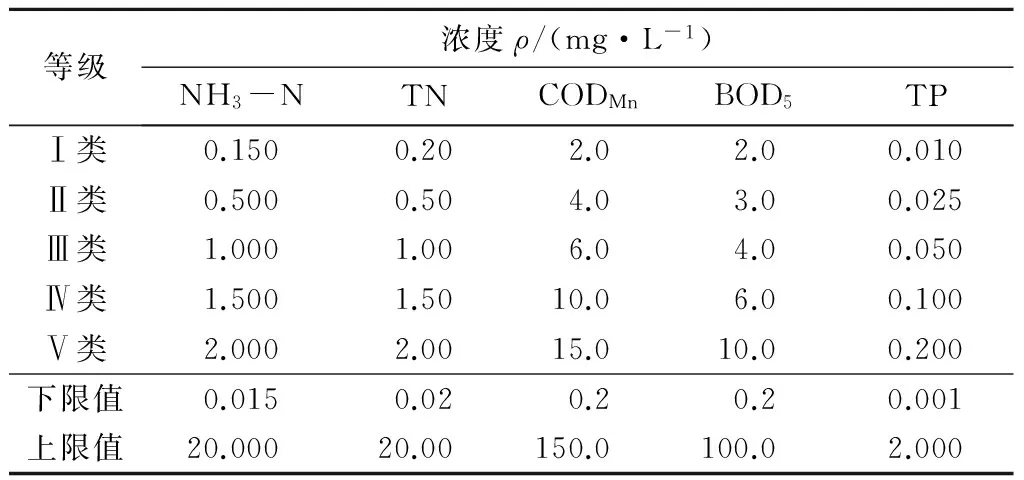
表2 5项水质评价因子分级标准值及限值

3.4 评价结果

(1) 从表1来看，SSO-PP模型水质评价结果与单因子法评价结果基本相同，但对于水质相对较好的断面1#，2#，4#，部分年度水质的评价结果要优于单因子法评价结果1～2级。由于单因子法采用最劣指标评价等级作为最终评价结果，评价不能客观反映水体综合水质状况。

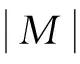
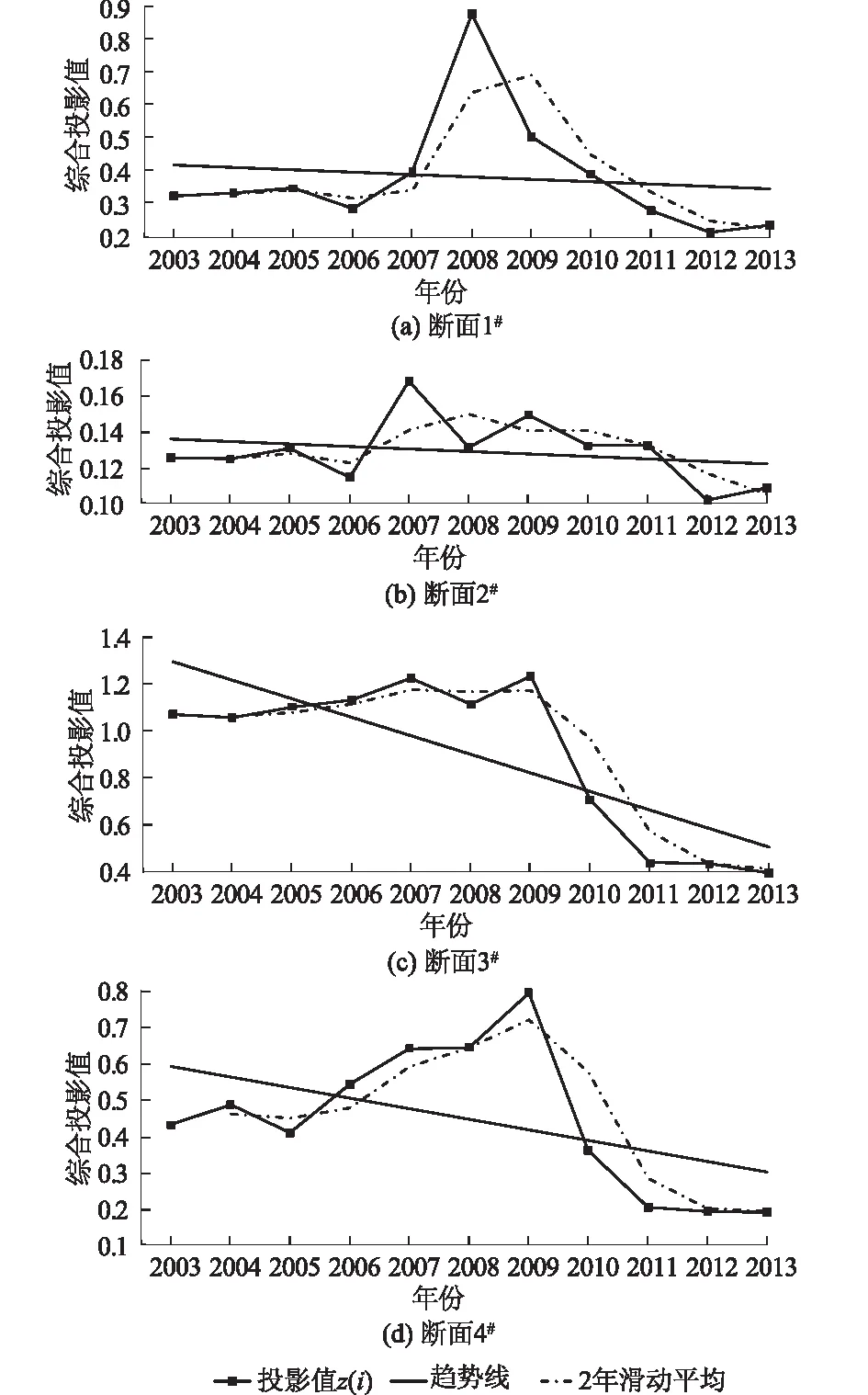
图1 不同断面各年度z(i)变化趋势及2年滑动平均过程Fig.1 Variation trends of z(i) and two-year moving average processes of different sections

4 结 论

(1) 针对PP模型在实际应用中存在的问题，提出SSO算法与PP模型相融合的SSO-PP水质综合评价模型，以滇池流域4个监测断面2003—2013年水质评价为例进行实例研究。结果表明，SSO-PP模型评价结果客观、合理，能够有效应用于水质综合评价。

(2) 本文所提出的生成数据样本、构造水质综合评价等级标准等方法可有效解决不同评价因子的水质综合评价问题，具有良好的通用性和实用价值。

[1] 梁增强,马民涛,杜改芳,等.基于信息熵权改进综合水质标识指数法及应用[J].四川环境,2013,32(3):38-42.

[2] 张俊华, 杨耀红, 陈南祥. 模糊物元模型在地下水水质评价中的应用[J]. 长江科学院院报, 2010, 27(9): 10-13.

[3] 田海翔,戴大刚,俞芳琴,等. 基于改进模糊层次分析法的龙华港水系水质综合评价[J].水资源保护,2013,29(5):55-58.

[4] 芦云峰, 谭德宝, 王学雷. 基于灰色模式识别模型的洪湖水质评价初探[J]. 长江科学院院报, 2009, 26(5): 58-61.

[5] 徐摇健,吴摇玮,黄天寅,等.改进的模糊综合评价法在同里古镇水质评价中的应用[J].河海大学学报(自然科学版),2014,42(2):143-149.

[6] 崔东文.水质综合评价的LM-BP 神经网络通用模型应用[J].水资源保护,2013,29(6):18-25.

[7] 李祚泳,张正健.基于回归支持向量机的指标规范值的水质评价模型[J].中国环境科学,2013,33(8):1502-1508.

[8] 黄 瑞, 张防修. 基于优化集对分析模型的水质综合评价方法[J]. 长江科学院院报, 2016, 33(5): 6-10.

[9] 李祚泳,张正健,余春雪.基于投影寻踪回归的指标规范值的水质评价模型[J].水文,2012,32(3):6-12.

[10]付 强,赵小勇.投影寻踪模型原理及其应用[M].北京:科学出版社,2006.

[11]王 柏,张忠学,李芳花,等.基于改进双链量子遗传算法的投影寻踪调亏灌溉综合评价[J].农业工程学报,2012,28(2):84-89.

[12]陈 曜,丁 晶,赵 永.基于投影寻踪原理的四川省洪灾评估[J].水利学报,2010,41(2):220-225.

[13]付 强,付 红,王立坤.基于加速遗传算法的投影寻踪模型在水质评价中的应用研究[J].地理科学,2003,23(2):236-239.

[14]陈广洲,汪家权,解华明.粒子群算法在投影寻踪模型优化求解中的应用[J].计算机仿真,2008,25(8):159-161,165.

[15]赵建强,戴青松,陈必科,等.基于人工蜂群—投影寻踪法的南方某河水质综合评价研究[J].节水灌溉,2014,(8):49-52.

[16]王明昊,董增川,马红亮.基于混合蛙跳与投影寻踪模型的水资源系统脆弱性评价[J].水电能源科学,2014,32(9):31-35.

[17]丁 红,刘 东,李 陶.基于改进人工鱼群算法的三江平原投影寻踪旱情评价模型[J].农业工程学报,2010,26(12):84-88.

[18]候景伟,孔云峰,孙九林.蚁群算法在需水预测模型参数优化中的应用[J].计算机应用,2012,32(10):2952-2956.

[19]CUEVAS E, CIENFUEGOS M, ZALDíVAR D,etal. A Swarm Optimization Algorithm Inspired in the Behavior of the Social-spider[J]. Expert Systems with Applications, 2013, 40(16): 6374-6384.

[20]王文川,雷冠军,尹 航,等.基于群居蜘蛛优化算法的水库防洪优化调度模型及应用[J].水电能源科学,2015,33(4):48-51.

[21]GB3838—2002,地表水环境质量标准[S].北京:中国环境科学出版社, 2002.

(编辑：陈 敏)

Comprehensive Evaluation of Water Quality in DianchiWatershed Based on SSO-PP model

WU Guang-qiong, FANG Jin-xin

(Lijiang Branch of Yunnan Provincial Hydrology Water Resources Bureau, Lijiang 674100, China)

In order to overcome the difficulty of determining the optimal projection direction in practical application of projection pursuit (PP) model, we propose a method of searching the optimal projection direction by using Social Spiders Optimization (SSO) algorithm, and hence building a SSO-PP model of water quality assessment. Four monitoring sections of Dianchi Lake watershed in Yunnan province from 2003 to 2013 were taken as case study. Fiver factors which have big influences on water quality were selected as assessment indicators: NH3-N, TN, CODMn, BOD5, and TP. The rating criteria of water quality were obtained according to index standard thresholds. Results showed that the assessment results of SSO-PP model were consistent with those of single-factor analysis, some superior for section 1#, 2#, and 4#. Kendall statistical test showed that the water quality of section 3#and section 4#improved apparently. The results of SSO-PP model are objective and reasonable, indicating that the model can be applied to assessing water quality effectively.

water quality assessment; projection pursuit; social spider optimization algorithm; swarm intelligence；Dianchi watershed

2015-08-22

吴光琼(1971-)，女，云南丽江人，工程师，主要从事水文与水资源等研究，(电话)13987049121(电子信箱)1258525280@qq.com。

10.11988/ckyyb.20150696

2016,33(10):18-23

X824

A

1001-5485(2016)10-0018-06