Global Dynamic Modeling of Electro-Hydraulic 3-UPS/S Parallel Stabilized Platform by Bond Graph
ZHANG Lijie, GUO FeiLI Yongquan, and LU Wenjuan
Global Dynamic Modeling of Electro-Hydraulic 3-UPS/S Parallel Stabilized Platform by Bond Graph
ZHANG Lijie1, 2,*, GUO Fei1, 2, LI Yongquan2, 3, and LU Wenjuan2, 3
123
Dynamic modeling of a parallel manipulator(PM) is an important issue. A complete PM system is actually composed of multiple physical domains. As PMs are widely used in various fields, the importance of modeling the global dynamic model of the PM system becomes increasingly prominent. Currently there lacks further research in global dynamic modeling. A unified modeling approach for the multi-energy domains PM system is proposed based on bond graph and a global dynamic model of the 3-UPS/S parallel stabilized platform involving mechanical and electrical-hydraulic elements is built. Firstly, the screw bond graph theory is improved based on the screw theory, the modular joint model is modeled and the normalized dynamic model of the mechanism is established. Secondly, combined with the electro-hydraulic servo system model built by traditional bond graph, the global dynamic model of the system is obtained, and then the motion, force and power of any element can be obtained directly. Lastly, the experiments and simulations of the driving forces, pressure and flow are performed, and the results show that, the theoretical calculation results of the driving forces are in accord with the experimental ones, and the pressure and flow of the first limb and the third limb are symmetry with each other. The results are reasonable and verify the correctness and effectiveness of the model and the method. The proposed dynamic modeling method provides a reference for modeling of other multi-energy domains system which contains complex PM.
screw bond graph, multi-energy domains, 3-UPS/S parallel mechanism, electro-hydraulic servo system
1 Introduction
Parallel manipulators become popular in different application fields, such as industrial, military, medical and other fields, owing to their good positional accuracy and rigidity. Applying PMs to stabilized platforms for insulating carrier turbulence have become a trend of development[1]..This paper focuses on the stabilized platform based on a three-DOF spherical PM driven by an electro-hydraulic servo system.
Dynamic modeling has been an important issue, because it plays a crucial role both in the dynamic performance analysis and control system development. There are several common methods for dynamic modeling of the PM, such as the Newton-Euler method, the Lagrange equation method, the principle of virtual work method and the Kane method[2–5]. YAHYAPOUR, et al[6], detached a 3-DOF spherical parallel manipulator, called the Agile Eye, into several subsystems and applied a consecutive synergy between kinematic analysis, Lagrangian and Newtonian approaches to build a model of the manipulator. The inverse dynamic problem of 3-UPS/S PM was solved using an approach based on the principle of virtual work by STAICU[7]. These methods foucs more on the modeling of the mechanical part of the system. Nevertheless, the complete PM system always including control system, drive system and the PM is a multi-energy domains coupling system. In this study, the parallel stabilized platform is driven by an electro-hydraulic servo system involving mechanical and hydraulic subsystems. Due to the mutual coupling between the subsystems, the common methods for dynamic modeling and equations derivation of the complete system become labor-intensive and consequently error-prone.
The bond graph method had been established by PAYNTER[8]in 1961 as a new approach to model, analyze and control various dynamic systems, in which energy bonds were utilized to define the energy flow between the physical elements of any system. It is a unified pictorial approach and has been extensively used for the design of electrical, mechanical, hydraulic, thermal and other systems[9–11]. For the multibody system, the simple kinematic relations are used to construct the bond graph model, the model by itself takes care of the Coriolis and centrifugal forces due to the inherent power conservative properties of a bond graph[12]. In Ref. [13] vector bond graphs and causality assignments have been introduced to bulid the multi body system. FILIPPINI, et al[14], implemented a general multibody system theory within a bond graph modeling framework. YILDIZ, et al[15–16], and DAMIC, et al[17], used classic vector bond-graph visualization to build dynamic model of a generalized Stewart platform, and the dynamic model includes all the dynamics and gravity effects, linear motor dynamics as well as the viscous friction at the joints. WANG, et al[18–19], built the dynamic models of the rigid and flexible robots of the spatial three degree of freedom with electric motors by the triditional one-dimensional bond graph and proposed the vector bond graph procedure for modeling robot systems. RAGUSILA and EMAMI[20]studied the bond graph model of a robotic leg mechanism, compared with the Lagrangian approach, a bond graph representation of the system is more simple and intuitive. They eliminated the bonds that have insignificant power flow and determined what mechanism is formed by the remaining dynamic elements to obtain the simpler model with the same significant dynamic characteristics of the original mechanism. BERA, et al[21–22], introduced modular bond graph modelling of planar mechanical systems, and emphasized the development of bond graph models of prismatic members. The bond graph model of the hydraulically driven planar(three-degrees-of-freedom) parallel manipulator is built and bond graph implementation of an overwhelming controller for the system is discussed[23]. However, for the spatial manipulator system, especially the spatial PM with strong coupling, multi closed-loops and multi body, the dynamic model based on bond graph will have excessively complex structures. Although there have been some simplified measures[24–25], it is still difficult to obtain the state equations and the analytical solution of the dynamic equations. As such, the bond graph is restricted in thewidespread development of PM dynamic modeling.
In 1993, MASCHKE, et al[26], proposed the concept of “Screw vector-bond graphs”. The screw vector-bond graphs combines the screw theroy with bond graph theroy by the dual product of twist and wrench equating to the power flow of bond graph. In Ref. [27], the screw bond graph is applied to the modeling of car wheel system. However, by now, there are few related studies given. As we can see, the screw theory can simply describe the spatial PM[28–30], so the screw bond graph can be used for the multi-energy domains global dynamic modeling of the PM system.
This paper is organized as follows. In section 2, the electro-hydraulic 3-UPS/S parallel stabilized platform is introduced. In section 3, the screw bond graph of the modulated transformer element and the moving body are defined, and then the global dynamic model of the system is built. In section 4, the global model of the system is verified by simulations and experiments.
2 Description of the Parallel Stabilized Platform
The parallel stabilized platform is composed of a 3-UPS/S parallel mechanism and an electro-hydraulic servo system, and its prototype is shown in Fig. 1(a). The system uses the same type of hydraulic cylinder and servo valve, and the 3-UPS/S parallel mechanism is shown in Fig. 1(b). The PM consists of a moving platform, a fixed platform, three driving limbs distributed by 120° and a pillar. The driving limb uses the hydraulic cylinder as a prismatic joint(P joint), and the piston rod is connected with the moving platform through the spherical joint(S joint) denoted byand the cylinder is connected with the fixed platform through the universal joint(U joint) denoted by. The pillar is connected with the fixed platform and connected with the moving platform through a spherical joint(S joint). The parallel stabilized platform has three rotational degrees of freedom, and mainly isolates roll and pitch attitude disturbance of motion carrier.
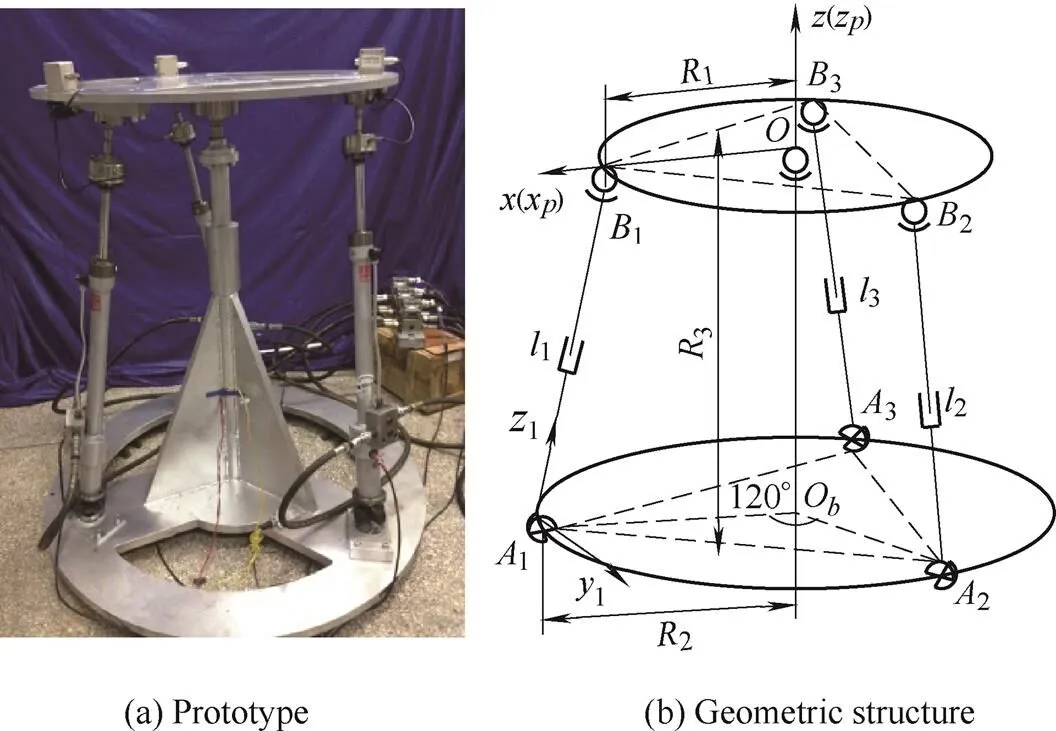
Fig. 1. Electro-hydraulic 3-UPS/S parallel stabilized platform
The inertial coordinate frameand the moving coordinate frameattached to the moving platform are both at the center of the spherical joint of the passive chain, as shown in Fig. 1(b). When there is no rotation of the moving platform, the framesandare coincident. The limb coordinate frameis at theuniversal joint with the axisand is along the hydraulic cylinder direction, the axisis perpendicular to the plane.
The T&T(title and torsion)[31]is selected to describe the mechanism posture. The rotation matrix between the frameandcan be expressed as
The rotation matrix between the frameandcan be expressed as
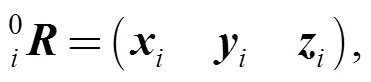
3 Global Bond Graph
Bond graph modeling is a unified pictorial approach to describe the energetic interactions and the information exchange between the subsystems or the elements based on power conservation. The only types of variables that will be needed to model physical system are represented by the power variables called effortand flowand energy variables called momentumand displacement. The subsystems or the elements are connected by the power bond. The bond graph has been widely used in many fields, and the further details can consult the Ref. [12]. In the following, the screw bond graph is introduced and improved for the modeling of the PM.
3.1 Screw bond graph
In the screw bond graph, the one-dimensional power bond is replaced by a six-dimensional power bond i.e. screw bond, and the effort variable and flow variable are replaced by a wrench and a twist, respectively. The notation of the screw bond is shown in Fig. 2.

Fig. 2. Notation of screw bond
Assume that there is a moving bodyand there are two coordinate framesand, then the transformation of the twist and the wrench of the bodyin the two coordinate framesandcan be represented as
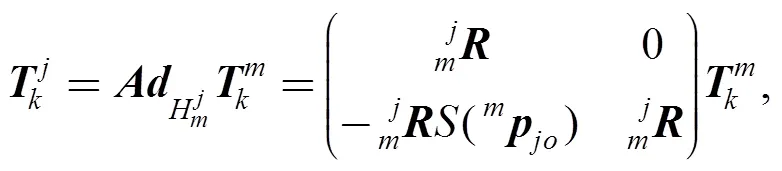

The coordinate transformation does not cause any power loss, and it satisfies the power conservation. So the coordinate transformation of the wrench and twist can be represented by the modulated transformer () element in the screw bond graph, and the notation is shown in the Fig. 3. The characteristic equations of the modulated transformer are given in Eqs. (1) and (2), and the modulus is.

Fig. 3. Screw bond graph of the modulated transformer
Actually, due to power conservation, the screw bond graph of the transformer element can be built via twist Eq. , and then the wrench Eq. can be derived based on the screw bond graph.
For the moving body, its inertia wrench can be represented in the framewhich is at the center of the mass and parallel to the inertial coordinate frame, as

Using the inward power sign convention and causality[7], the screw bond graph of the moving bodycan be built as shown in Fig. 4.
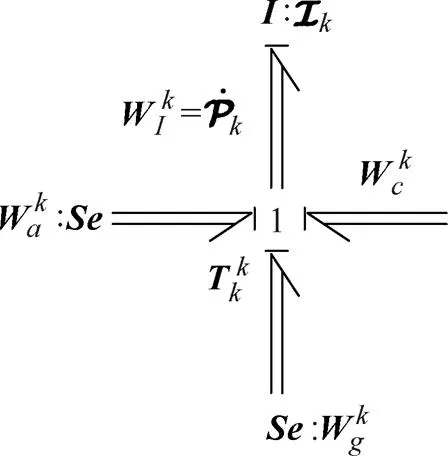
Fig. 4. Screw bond graph of the moving body
3.2 Screw bond graph of the parallel mechanism
Because the structure of each limb of the parallel mechanism is the same, we firstly take one of the limbs to analyze.
The center of the mass of the upper and down rod which are the piston rod and the cylinder, are,, respectively. The local coordinate system is built as follows and depicted in Fig. 5. The coordinate frames at the center of mass of each rod are(=1, 2, 3) andwhich are parallel to the coordinate frame. The coordinate frames,andare the joint coordinate frames, and the origins of the frames are the contact pointand the rotation center pointsand, respectively. Among them, the framesandare parallel to the frame. The axisof the frameis along the fixed axis of the universal joint, then relative to frame, the direction cosines of unit vector can be expressed as,,, and axisis perpendicular to the axisand, soand.
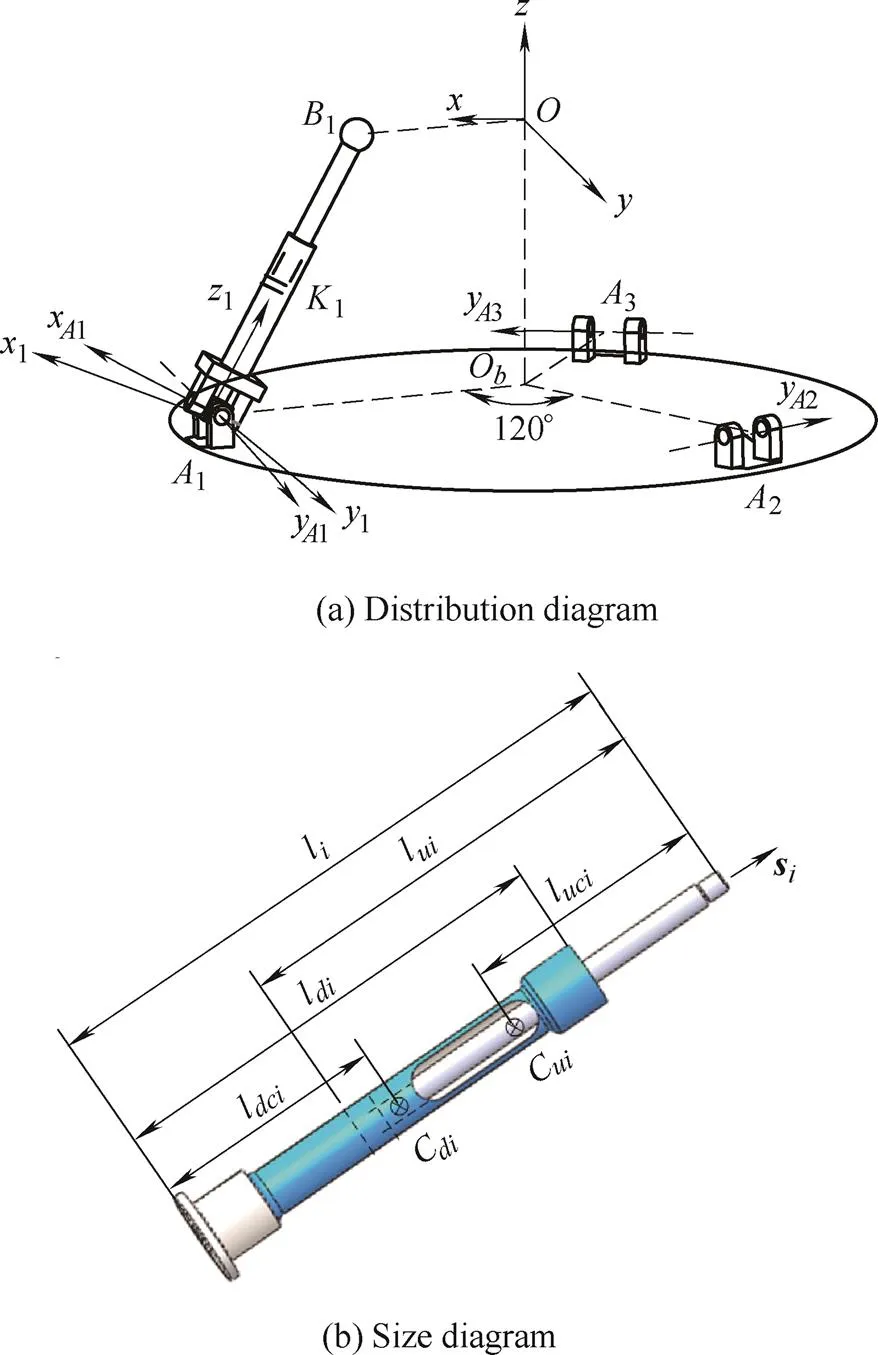
Fig. 5. Structural diagram of one limb
For the prismatic joint of the limb, by Eq. , the twists of the upper and down rod can be expressed in the frameas
Then the relative twist is
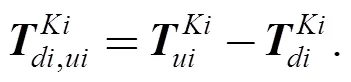
According to Eqs. , and the screw bond graphs of the moving body and the modulated transformer, the screw bond graph of the prismatic joint can be built, as depicted in Fig. 6.
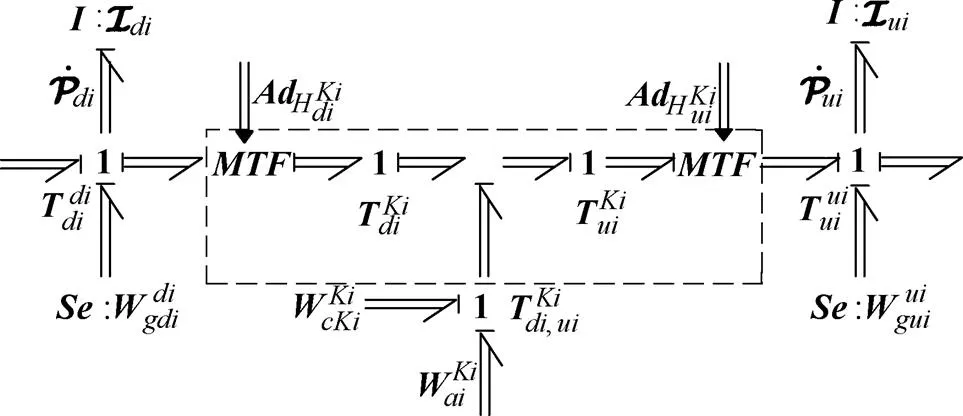
Fig. 6. Screw bond graph of the prismatic joint
In the screw bond graph of the prismatic joint, the wrenches are
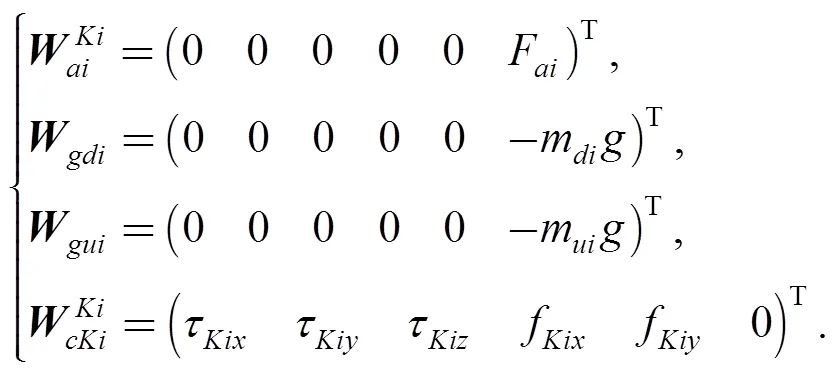
The dotted part in Fig. 6 can be treated as a modular structure. The screw bond graphs of the universal joint and spherical joint can be built with the reference to the prismatic joint. The complete screw bond graph of one limb of the parallel mechanism can be constructed.
3.3 Bond graph of the electro-hydraulic servo system
The parallel stabilized platform is driven by an electro-hydraulic servo system, as Fig. 7(a) shows the principle diagram of the hydraulic system of one limb, and Fig. 7(b) shows the principle diagram of the valve control non-symmetry hydraulic cylinder.
In Fig. 7, portandrepresent control ports, portandrepresent oil port,andis theoil supply pressure and return pressure,,and,represent the flow and pressure of the two chambers of the cylinder,represents leakage flow,andrepresent effective areas, andrepresents the displacement of the valve core.
- and- elements represent characteristics of the components of the electro-hydraulic servo system, the bond graph of the hydraulic system can be built[32], as shown in Fig.8.andelements represent the oil filter,andelements represent oil cooler,elements represent relief valves,andelements represent accumulator, andandelements represent the hose. These units are designed in order to ensureandof the system, so the hydraulic system can be simplified as valve control system, as the bold part in Fig. 8. In the valve control system,elements represent the variable hydraulic resistance coefficient,element represents the leakage resistance coefficient,element represents the friction coefficient,elements represent the capacitive of the two chambers of the cylinder. The variable hydraulic resistance coefficient and the capacitive of the two chambers are

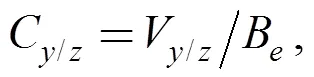
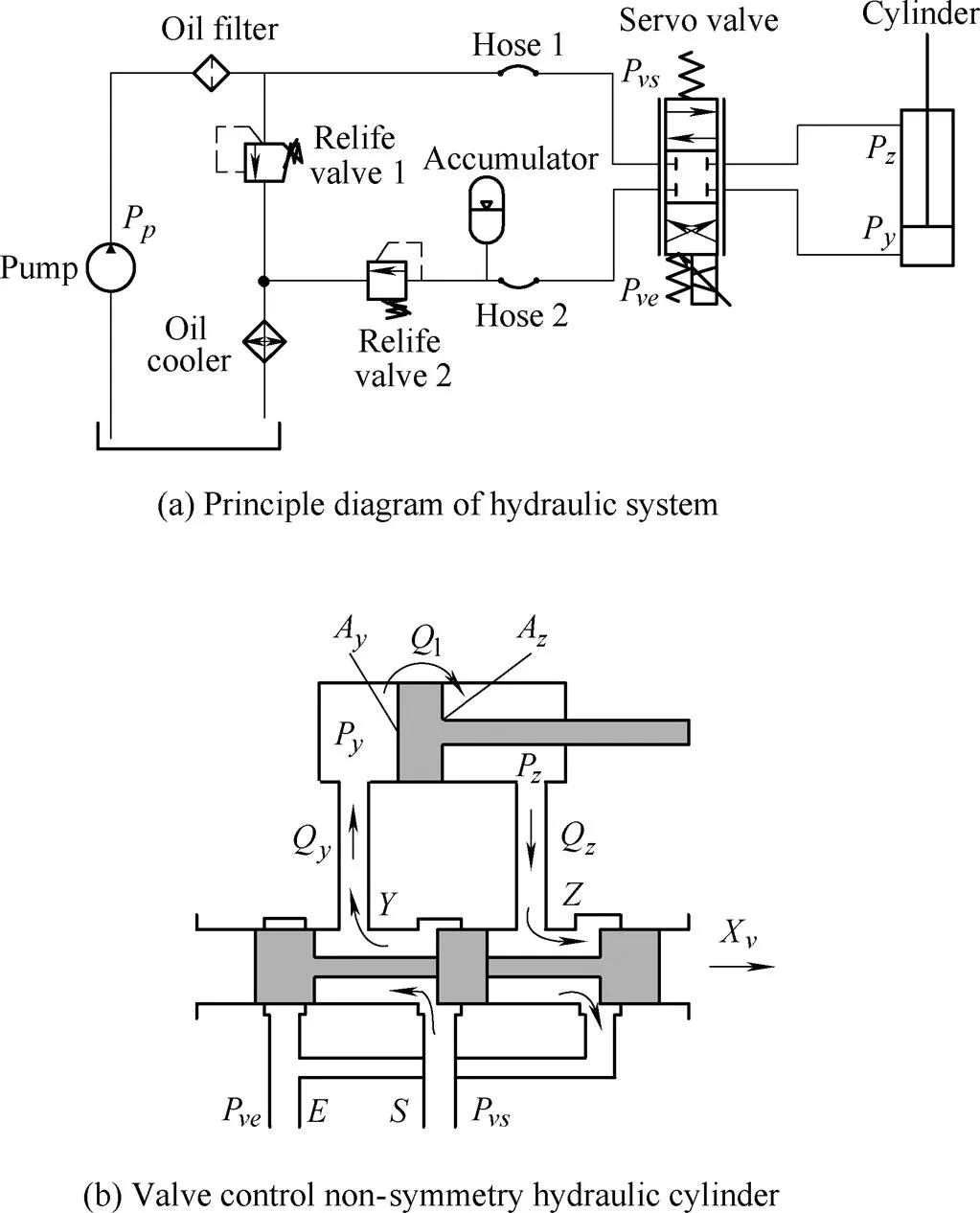
Fig. 7. Electro-hydraulic servo system
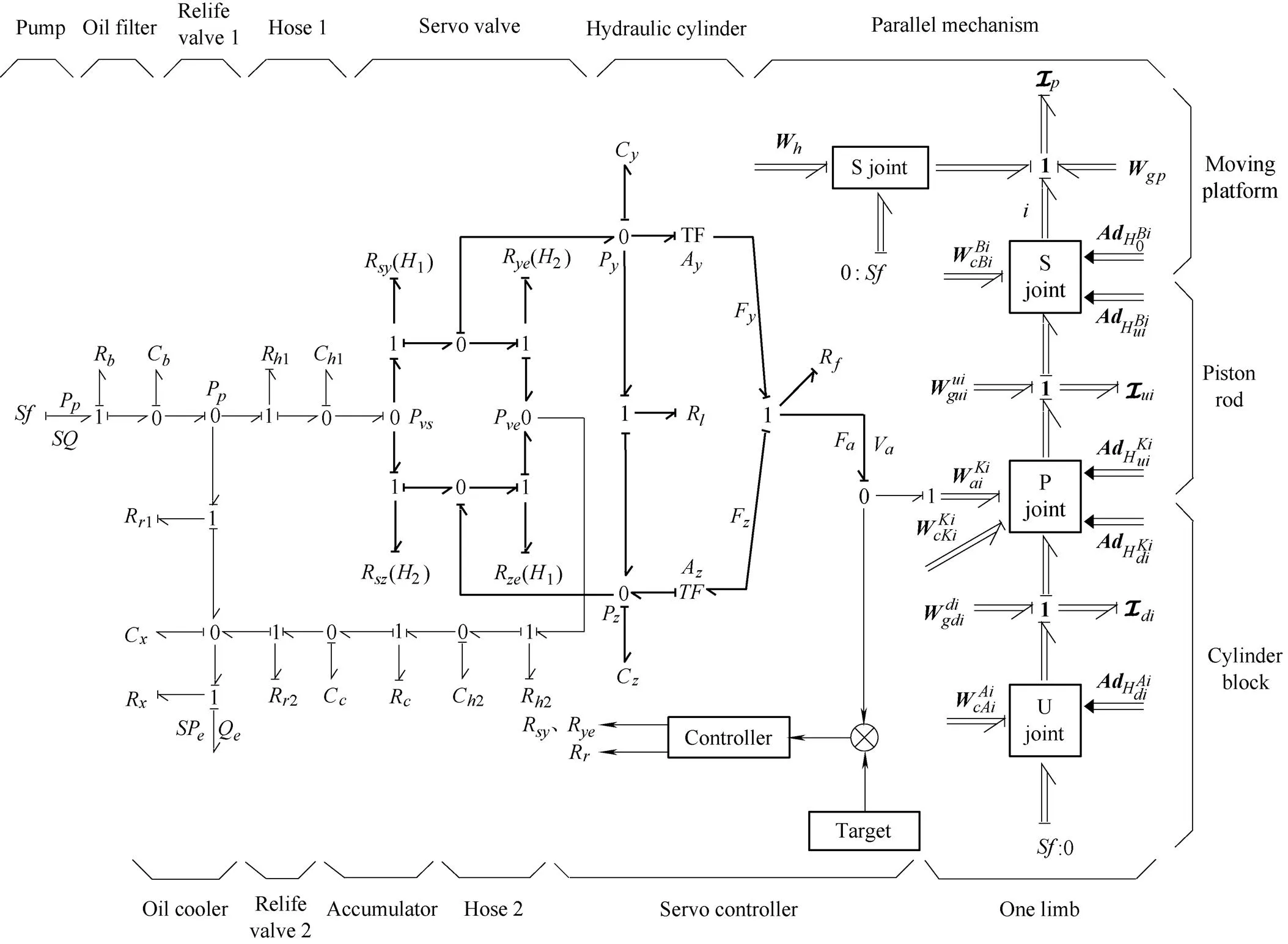
Fig. 8. Global bond graph of one limb of the parallel stabilized platform
3.4 Global bond graph of the parallel stabilized platform
Combining the screw bond graph of the mechaism with the bond graph of the eletro-hydraulic servo system, the global bond graph of one limb of the parallel stabilized paltform can be constructed, as shown in Fig. 8. Then the global bond graph of the complete parallel stabilized paltform can be obtained by connecting the three limbs to the moving platform as the physical model of the system.
According to the global bond graph, the corresponding state equations of the mechanism are

where

and transformation matrixes can be obtained by Eq. , since the framesandare parallel to the frame, and the frameandare parallel to the frame, there is.
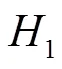
Based on above modes, the state equations of the valve control system are derived, as:

The supplementary equations are

And the energy exchange between the mechanical system and the hydraulic system is

4 Validation of the Bond Graph Model
The inverse dynamics is the basis of the dynamic parameter identification and control study of the parallel stabilized platform. Hence, according to the global bond graph of the system and the state equations, the validation is carried out for the inverse dynamics.


Table 1. The parameters of the parallel stabilized platform
 Chinese Journal of Mechanical Engineering2016年6期
Chinese Journal of Mechanical Engineering2016年6期
- Chinese Journal of Mechanical Engineering的其它文章
- Surface Topography and Roughness of High-speed Milled AlMn1Cu
- Digital Evaluation of Sitting Posture Comfort in Human-vehicle System under Industry 4.0 Framework
- Thermo-physical Characteristics of Nickel-coated Aluminum Powder as a Function of Particle Size and Oxidant
- Effect of Magnetic Field on Forced Convection between Two Nanofluid Laminar Flows in a Channel
- Gas Film Disturbance Characteristics Analysis of High-Speedand High-Pressure Dry Gas Seal
- Method for Evaluating the Reliability of Compressor Impeller of Turbocharger for Vehicle Application in Plateau Area
