调频相关延迟差分混沌键控的通信模型及性能

王 娟 ， 张 爽 ， 甄春阳， 丁 群

(1.黑龙江大学 电子工程学院， 哈尔滨 150001；



调频相关延迟差分混沌键控的通信模型及性能

王 娟1，2， 张 爽2， 甄春阳2， 丁 群1

(1.黑龙江大学 电子工程学院， 哈尔滨 150001；

2.黑龙江科技大学 电子与信息工程学院， 哈尔滨 150022)

针对现有差分混沌键控数据传输速率低、误码率高、保密性差的问题，结合调频差分混沌键控FM-DCSK和相关延迟差分混沌键控CD-DCSK，提出一种新型的调频相关延迟差分混沌键控FM-CD-DCSK通信方法，通过频率调制使信息比特能量恒定，利用相关延迟可同时传输2位信息。结果表明：在扩频因子、信噪比和信号干扰比相同的情况下，FM-CD-DCSK的通信性能明显优于FM-DCSK和CD-DCSK。对于不同的信噪比，选择合理的扩频因子，能够实现该通信方案的最优性能。

数字保密通信； 混沌键控； 调频相关延迟差分混沌键控

0 引 言

基于非相干解调的差分混沌键控由于避免了信道估计和载波同步，因此，成为数字保密通信研究的主要方向。混沌信号具有宽带、类噪声、难以预测、对初始条件十分敏感等，其保密性能明显优于传统的伪随机序列[1-2]。混沌保密通信分为混沌掩盖、混沌参数调制、混沌扩频和混沌键控。混沌掩盖在信号振幅大于5 V时将暴露出有用信号特点，当受到噪声干扰时同步系统容易失调，因此，难以在实际中应用[3]。混沌参数调制将有用信号隐藏在系统参数中，虽保密性能优于混沌掩盖，但仅适用于缓慢变化的信号，且参数调制对外界干扰极度敏感，使其通信效率大大降低[4]。混沌扩频利用混沌信号作为载波展宽信号频谱，既能有效消除多径干扰，又能降低信号被截获的概率，但是从接收信号中恢复出混沌同步信号非常困难[5]。

混沌键控在抗噪声、抗多径衰落和抗参数敏感能力上相对较好，利用混沌信号的类噪声特性达到隐藏信号的目的，由于功率谱密度较低使其更难检测和截获[6]。混沌键控按解调方式分为相干[7]和非相干[8]两类，基于同步的相干解调由于混沌的初值敏感性使得在接收时重建同步信号异常困难，而非相干解调则无需复杂的同步装置电路实现简单[9-10]。为了避免从接收信号中恢复出同步的混沌载波，差分混沌键控DCSK、相关延迟键控CDSK等通信方案成为国内外学者的研究热点。CDSK在传输过程中将参考信号和信息信号同时传输，虽然提高了频带利用率，但由于混沌信号和延迟信号存在互相关性导致误码率上升。DCSK在一个比特周期内，仅有一半时间传输信息信号，另一半时间传输参考信号，虽然频带利用率低，但却具有良好的误码性能[11]。为使数字保密通信具有更为优越的有效性、可靠性和保密性，笔者结合调频差分混沌键控FM-DCSK和相关延迟差分混沌键控CD-DCSK，提出一种新型的调频相关延迟差分混沌键控FM-CD-DCSK。

1 FM-CD-DCSK混沌键控

在目前应用较为广泛的差分混沌键控中，FM-DCSK通过频率调制使信号的比特能量保持恒定，避免出现判决错误从而降低误码率，但其数据传输速率和频带利用率较低，且在一个信号传输周期内同一条信道传输的是同相或反相关系的参考信号和信息信号，中途被截获后通过相关分析等攻击方法很容易提取出发送信息。CD-DCSK在同一比特内的前后半个周期以穿插形式传输2位信息，使其数据传输速率和频带利用率提高到FM-DCSK的2倍，由于信道传输的信号是均匀的无重复信息，其安全性能也得到进一步提高。但是由于混沌信号的非周期特性，经CD-DCSK调制后比特能量会随时间变化，从而引起判决问题导致误码率提高，因此，提出将FM-DCSK、CD-DCSK相结合得到一种新型混沌键控FM-CD-DCSK模型，其模型如图1所示。

图1 FM-CD-DCSK混沌键控发射模型Fig. 1 FM-CD-DCSK chaos shift keying transmitting model

1.1 发射模型

由图1可见，设高频载波c(t)=Accosεct，则振幅随机变化的混沌信号x(t)经过频率调制后输出为

(1)

式中：kf——调频系数；

x′(t)——振幅恒定而频率随机变化的混沌调频信号。

x′(t)作为载波进行CD-DCSK混沌键控，将通过串并转换得到的高低位信号a1、a2映射到传输信息内，a1和a2分别代表传输“+1 +1, -1+1, +1-1,-1-1”四种情况。在前半个符号周期内，传输信息s1(t)是参考信号x′(t)与信息信号a1x′(t-Tb/2)的叠加；在后半个符号周期内，传输信息s2(t)是参考信号x′(t)与信息信号a2x′(t-Tb)的叠加。则在第l个符号周期内， FM-CD-DCSK调制端发送的信号为

(2)

式中：a1x′(t-Tb/2)、a2x′(t-Tb)——信息信号。

信息序列经过双极性变换后，若a1和a2的符号为“1”，则信信和参考信号相同；如果a1和a2的符号为“0”，那么信息和参考信号相反。因此，发送的信息包含在两个相邻码元样值的相关值中。

1.2 接收模型

如图2所示，假设发送信号经过信道传输时受到加性高斯白噪声n(t)的干扰，在解调端利用串并转换将接收信号进行逆穿插恢复，并将参考信号和信息信号进行相关运算，则相关器的输出分别为

n(t)][s1(t-Tb/2)+n(t-Tb/2)]dt=

(3)

(4)

式(3)和式(4)中，第一项均为有用的信号项，其余三项的相关值均为零。当y1(t)、y2(t)分别通过判决电路时，将判决电路的门限值设为零。如果y1(t)、y2(t)>0，则判决输出z1(t)、z2(t)为“+1”；如果y1(t)、y2(t)<0时，则判决输出z1(t)、z2(t)为“-1”，最终，z1(t)、z2(t)通过并串转换解调输出。

图2 FM-CD-DCSK混沌键控接收模型

Fig. 2 FM-CD-DCSK chaos shift keying receiving model

2 FM-CD4DCSK的保密通信性能

为了验证FM-CD-DCSK的数字保密通信性能，在Matlab/Simulink中对基于高斯白噪声信道的FM-CD-DCSK键控模型进行仿真分析，并与传统混沌键控FM-DCSK、CD-DCSK性能进行比较。仿真中采用一维离散混沌映射logistic生成混沌信号，系统参数和初值分别设置为μ=3.98和x0=0.4。

2.1 通信性能

FM-CD-DCSK误码性能随扩频因子的变化如图3所示，仿真时间设置为2 000 s，扩频因子分别设置为M=4、8、16和24。通过仿真可以发现，当信噪比SNR=Eb/N0<8 dB时，FM-CD-DCSK在不同扩频因子下具有近似相同的误码性能。当8 dB24 dB时，FM-CD-DCSK在不同扩频因子下的误码性能趋于稳定，不再随信噪比的增大而发生变化。因此，在一定扩频因子条件下，适当选择信噪比的取值对于FM-CD-DCSK误码性能的影响非常重要。

图3 FM-CD-DCSK的误码性能

FM-CD-DCSK误码性能随信噪比的变化如图4所示，仿真时间设置为2 000 s，信噪比分别设置为5、10、15和20 dB。通过仿真可以看出，FM-CD-DCSK的误码率随着信噪比的增加而降低。同时，当SNR=5、10 dB时，扩频因子对误码率的影响并不明显；当SNR=15、20 dB时，误码率会随着扩频因子的增大而降低，当扩频因子增大到某一临界值后，误码率反而会随着扩频因子的增大而升高，因此，在一定信噪比条件下，适当选择扩频因子的取值对于FM-CD-DCSK误码性能的影响非常重要。

图4 FM-CD-DCSK的误码性能

FM-CD-DCSK、FM-DCSK和CD-DCSK三种混沌键控误码性能随扩频因子的变化如图5所示。

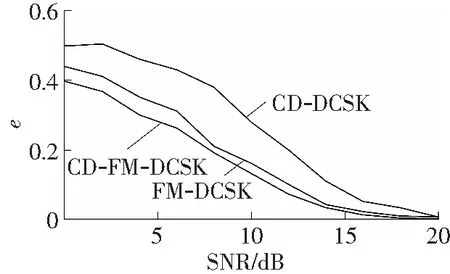
a M=4

b M=8

c M=16

d M=24

Fig. 5 Performance comparison of three kinds of chaos shift keying under different spreading factors

由图5可见，仿真时间设置为2 000 s，扩频因子分别设置为M=4、8、16、24。通过对比可以发现，在低信噪比情况下，FM-CD-DCSK在不同扩频因子下的误码性能明显优于FM-DCSK和CD-DCSK；在高信噪比情况下，FM-CD-DCSK在不同扩频因子下的误码性能虽仍优于FM-DCSK和CD-DCSK，但随着信噪比的增大三者之间的差异逐渐减小；当信噪比增大到16 dB以上时，FM-CD-DCSK的误码率趋近于0；当信噪比增大到20 dB以上时，FM-DCSK和CD-DCSK的误码率均趋近于0。由此可以说明，FM-CD-DCSK相较于FM-DCSK和CD-DCSK具有更为优越的误码性能。

2.2 抗干扰性能

FM-CD-DCSK误码性能在不同信噪比下随信号干扰比的变化，如图6所示，仿真时间设置为2 000 s，信噪比分别设置为SNR=5、10、15、20 dB。通过图6可以看出，FM-CD-DCSK的误码率随着信号干扰比的增加而降低。在信号干扰比SIR相同的情况下，信噪比取值越大，FM-CD-DCSK的误码率取值越低。由此可见，为保证FM-CD-DCSK的通信性能，信号干扰比和信噪比的合理取值是非常必要的。

图6 不同信号干扰比下信噪比对FM-CD-DCSK误码性能的影响

Fig. 6 Effect of SNR on performance of FM-CD-DCSK under different SIRS

FM-CD-DCSK、FM-DCSK和CD-DCSK三种混沌键控误码性能随信号干扰比的变化如图7所示，随着信号干扰比的不断增大，三种混沌键控的误码性能均逐渐增强。在信号干扰比相同的情况下，FM-CD-DCSK的误码性能明显优于FM-DCSK和CD-DCSK，这说明FM-CD-DCSK的抗干扰性相比传统混沌键控得到了明显提高。

图7 三种混沌键控在不同信号干扰比下的性能比较

Fig. 7 Performance comparison of three kinds of chaos shift keying under different SIRS

2.3 保密性能仿真分析

FM-CD-DCSK图像传输性能如图8所示。在FM-CD-DCSK混沌键控中对图像信息进行模拟传输，图8a为调制端发送图像，图8b为调制端加密图像，图8c为解调端接收图像。通过仿真可以看出，FM-CD-DCSK具有较为优异的安全性能。

a 发送图像 b 加密图像 c 接收图像

3 结束语

通过对传统差分混沌键控的分析，将FM-DCSK和CD-DCSK相结合，提出一种新型混沌键控FM-CD-DCSK的通信系统模型。该系统通过频率调制使信息比特能量恒定，又利用相关延迟同时传输 2 位信息，兼具FM-DCSK和CD-DCSK的优点。通过对FM-CD-DCSK进行通信性能、抗干扰性能和保密性能的仿真分析，可以得出扩频因子、信噪比和信号干扰比对其误码性能的影响，通过合理的参数设置能够实现该通信方案性能的最优。同时，在扩频因子、信噪比和信号干扰比相同的情况下，FM-CD-DCSK的误码性能明显优于FM-DCSK和CD-DCSK，能够实现更为高速安全、稳定可靠的数字保密通信。

[1] WANG JUAN, DING QUN. Excellent performances of the third-

level disturbed chaos in the cryptography algorithm and the spread spectrum communication[J].Journal of Information Hiding and Multimedia Signal Processing, 2016, 4(7): 826-835.

[2] WANG JUAN, DING QUN. Investigation on the simulation of one-dimensional discrete chaotic digital generation circuit[C]//IEEE International Conference on Robot, Vision and Signal Processing, 2015(11): 180-184.

[3] HE S Y. The research of synchronization communication technology based on chaotic masking[J]．IEEE International Conference on Intelligent Computing and Intelligent Systems， 2009(3): 267-270. [4] 王佳楠， 丁 群. 一种新的混沌数字保密通信实现方案[J]. 通信技术， 2011， 44(2): 75-77.

[5] 杨 华， 蒋国平.一种改进型差分混沌键控通信方案[J]. 南京邮电大学学报: 自然科学版， 2013， 33(1): 29-32.

[6] YANG HUA, JIANG GUOPING, DUAN JUNYI. Phase-separated DCSK: a simple delay-component-free solution for chaotic communications[J]. IEEE Transactions on Circuits and Systems-II: Express Briefs, 2014, 61(12): 967-971.

[7] DEDIEU H, KENNEDY M P, HASLER M. Chaos shift keying: modulation and demodulation of a cliaotic carrier using self-synchronizing Chua’s circuit[J]. IEEE transactions on Circuits and Systems-II: Analog and Digital Signal Processing, 1993, 40(10): 634-642.

[8] KOLUMBAN G, VIZVARI B, SCHWARZ W. Differential chaos shift keying: a robust coding for chaos communications[C]// Proceedings of the 4th International Workshop on Nonlinear Dynamics of Electronics Systems, Seville, 1996: 87-92.

[9] 贺利芳， 张 刚， 张天骐． 一种基于 DCSK 的数字保密通信系统[J]． 电子技术应用， 2012， 38(7) : 103-106．

[10] YANG H, JIANG G P. Reference modulated DCSK:a novel chaotic communication scheme[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2013, 60(4): 232-236.

[11] SUSHCHIK M，TSIMRING L S，VOLKOVSKII A R. Performance analysis of correlation-based communication schemes utilizing chaos[J]．IEEE Transaction on Circuits and Systems， 2000, 47(12 ): 1684-1691．

(编校 李德根)

Communication model and performance of frequency modulation correlated delay differential chaos shift keying

WangJuan1,2,ZhangShuang2,ZhenChunyang2,DingQun1

(1.Electronic Engineering Institute, Heilongjiang University, Harbin 150001， China；2. School of Electronics & Information Engineering, Heilongjiang University of Science & Technology, Harbin 150022， China)

This paper introduces a novel frequency modulation correlated delay differential chaos shift keying FM-CD-DCSK a combination of the frequency modulation differential chaos shift keying FM-DCSK and correlated delay differential chaos shift keying CD-DCSK, as an alternative to the existing differential chaos shift keying which suffers from a lower data transmission rate, a higher bit error rate, and a poor confidentiality. This FM-CD-DCSK enables the constant information bit energy by frequency modulation and the simultaneous transmission of 2 bits of information using the relevant delay. The simulation demonstrates that, given the same spread spectrum factors, signal to noise ratio, and signal to interference ratio, FM-CD-DCSK features a significantly better communication performance than both FM-DCSK and CD-DCSK; and the selection of reasonable spread spectrum factor for different signal-to- noise ratios can provide an optimal performance of FM-CD-DCSK.

digital secure communication； chaos shift keying； frequency modulation correlated delay differential chaos shift keying

2016-08-16

国家自然科学基金项目(61471158)；教育部高等学校博士学科点专项科研基金项目(20132301110004)

王 娟(1981-)，女，黑龙江省佳木斯人，副教授，博士研究生，研究方向：无线信号的传输处理及安全，E-mail：76115347@qq.com。

10.3969/j.issn.2095-7262.2016.05.023

TN918

2095-7262(2016)05-0581-05

A