寻找规律轻松解答
□赖丰秋
寻找规律轻松解答
□赖丰秋
小朋友,数学中有些题目看起来不容易解答:数据大,难以计算;图形多,难以计数。其实,只要你细心观察,寻找出规律,同样可以使那些看似复杂的题目变得简单易解。
一、寻找数字排列规律
计算是学好数学的基础,我们要学好数学,必须要具有一定的计算能力。有些计算只要你能寻找出数字排列的规律,不但可以省去繁杂的计算过程,而且能使解答更加准确、快速。
例如:1×1=1,11×11=121,111×111=12321,1111× 1111=____,11111×11111=____,111111×111111=____。
经过观察,我寻找到了其中的规律。算式的规律是:每一题中的两个因数都相同,并且每个数位上的数字都是1。积的规律是:因数是几位数,积就按1、2、3……的顺序排列到几,然后倒回来排列到1。找到了积数字的排列规律,后面算式的答案就能准确、轻松地得出了:1111×1111=1234321,11111×11111=
123454321,111111×111111=12345654321。
二、寻找计算方法规律
数学中的许多计算都有着奇特的小窍门。怎样使计算既准确又快速呢?寻找计算方法的规律有时显得格外有效。
例如,计算下列一组题:
62×68,37×33,81×89,44×46,95×95,56×54。
经过观察,我发现这是一组有规律的乘法算式。首先,两个因数都是两位数,其次,这两个因数十位上的数字相同,个位数字的和都是10,即:首同尾和10。那么,它们的积又有什么规律呢?我用竖式计算出了前两题的答案,62×68=4216,37×33= 1221。经过观察比较,我发现它们的积有共同点:前两位数=头×(头+1),后两位数=尾×尾。这种方法正确吗?可以用第三题来验证。用竖式计算出81×89的结果是7209,符合这个规律。接下的三题我几秒钟就解决了,44×46=2024,95×95= 9025,56×54=3024。我又举了几个这样的例子,发现这种计算方法都能适用。
三、寻找图形计数规律
在我们的数学学习中,还经常出现计算图形总数的题目。
例如:数一数,下面的图形中各有几个角?
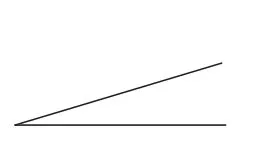
图1
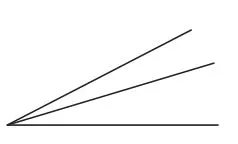
图2

图3
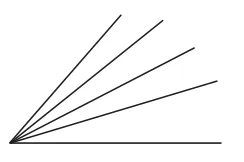
图4
解答这类题目,应先给每个小角标上序号,再分别数出由1个、2个、3个……小角组成的角各有几个,最后加起来。但是,仍
有不少同学在计算角的个数时会遗漏或重复,出现错误。能不能寻找出计算图形个数的规律来,使大家算得又准又快呢?我几经琢磨后发现了图形计数的规律:图中有几个单独的小角,角的总数=1+2+……+几。如图2中角的个数为1+2=3(个);图3中角的个数为1+2+3=6(个);图4中角的个数为1+2+3+4=10(个)。这个规律还适用于计算线段的条数、三角形的个数等。
小朋友,数学王国里还藏着数不尽的规律,只要你细心观察、认真思考,一定能比我寻找到更多的规律,倍加轻松地解决更多的数学问题。
(作者单位:福建省长汀县实验小学)
第9页参考答案
这位老人的年龄是(100÷ 10+15)×4-12=88(岁)。

