对 《定期检修系统的可靠性建模与仿真》的商榷

丁定浩

对 《定期检修系统的可靠性建模与仿真》的商榷

丁定浩

商榷论文给出了描述连续工作状态下的定期检修系统的可靠性解析模型和仿真框图，但文中并没有涉及失效单元的检修方式和检修能力，并且没有考虑检修中的备件保障，因此难以正确地反映客观实际。通过示例指出了文中的不合理之处,希望引起相关人员的重视。

定期检修系统；可靠性解析模型；数字仿真；连续工作状态；间断工作状态

0　引言

在经典的可靠性模型研究中，存在停机检修和联机检修两类模型。停机检修是指当工作中的冗余单元发生失效时，不能立即对其检修，必须等到任务结束后或在下次开机前对其进行检修；联机检修是指当工作中的冗余单元发生失效时容许在不停机的条件下立即对其进行检修，修复后随即接入工作直到任务结束[1]。

但在实际的工程中，还需要进行定期检修，由此需要研究定期检修的模型。例如：对于在相控阵雷达天线射频收发阵列中的冗余收发单元，在整机性能参数符合指标的情况下，高悬空间的天线环境使得不适宜频繁地在每次任务结束后都对已经失效了的冗余收发单元进行检修。又如：对于密封在油箱中的、包含有冗余单元在内的高压整流硅堆的高压电源，更不可能在每次任务结束后都对其进行检修；因为是高压，不可能在油箱外的引线处对其进行检测，必须打开油箱进行。打开油箱后，当发现有失效单元时便对其进行更换；但当发现无失效单元时，打开和封闭油箱的一系列工作便成了无效的劳动。对于此类系统，必须采用定期检修的方式进行检修，即工作过程中每隔规定的周期后，才对已经失效了的冗余单元进行检修，再重复前面的工作与检修的整个过程。当任务剖面为连续工作状态时，检修失效单元时是不停机的。

1　定期检修的可靠度模型

定期检修的可靠度模型，笔者在参考文献 [2-3]中已经介绍过，它适用于任务剖面为间断工作状态。因此，在使用定期检修的可靠度模型时必须权衡各种条件，最终确定合适的周期进行检测检修，具体的解析模型如下所示：

式 （1）中：T0——定期检修周期；

ts——任务持续工作时间。

由式 （1）可知，对于由串联结构构成的系统而言，定期检修与停机检修是相同的；而对于存在冗余结构的系统而言，两者则有明显的差别。从物理概念上也不难理解，这是因为，对于由串联结构构成的系统，一旦系统发生故障，则必须立即对其进行检修，否则系统将不能继续工作；而对于存在冗余结构的系统，当其中的冗余单元发生故障时，因为冗余单元失效并不影响系统正常工作，所以可以不立刻对故障进行检修，但当系统中的冗余单元减少时，系统的可靠性会降低。

定期检修可以在不修复已经发生故障的冗余单元的条件下而使系统继续工作，但要以任务可靠度的降低为代价。但是，这一问题可以通过增加冗余单元数来补偿。冗余单元的补偿数量，可以通过式（1）来计算。

计算的目标值是Rs（ts|T0），即在定期检修周期为T0条件下的任务可靠度的要求值，由此可以计算出在定期检修条件下要求可靠度保持原有的水平时冗余单元增多的数量。

2　商榷论文的解析模型和仿真框图不能完整地反映客观实际

商榷论文最终讨论的模型[4]不是任务剖面为间断工作状态的定期检修的任务可靠度模型，而是任务剖面为连续工作状态的平均致命故障间隔时间模型。这两者都是定期检修模型但又描述的是完全不同的状态和不同的参数。前者的任务剖面是间断工作状态，而后者的是连续工作状态；前者的参数是任务可靠度，而后者的是平均致命故障间隔时间（MTBCF：Mean Time Between Critical Failure）。商榷论文的示例显示其参数是连续工作状态下的平均致命故障间隔时间。

这种模型的过程应该是系统在定期检修周期中保持正常工作，在周期的最后时刻，在系统继续保持正常工作的时间内，要求修复已经失效了的冗余单元，随后又转入新一轮定期检修周期，重复上述过程，直到发生系统失效为止。

从商榷论文给出的解析模型和仿真框图可以看出，两者均没有涉及失效单元的检修方式，而失效单元的检修方式涉及修复时间的长短，因此，商榷论文就不可能反映定期检修客观过程的真实性。

检修方式通常包括3种，即逐个检修方式、同时检修方式和有限同时检修方式。逐个检修方式是指对一批已经失效的单元只能一个修复后再修复另一个，逐一地进行修复，直到全部修复为止；同时检修方式是指对所有的失效单元同时进行检修；有限同时检修方式是指同时对有限数量的失效单元进行检修。

不言而喻，对于同一批失效单元，这3种检修方式的修复时间是完全不同的。即，同时检修方式的平均修复时间最短，有限同时检修方式的平均修复时间次之，逐个检修方式的平均修复时间无疑是最长的。

顺便指出，对于多个失效单元同时检修的平均修复时间，笔者已经纠正了美国MIL-HDBK-338《电子设备可靠性设计手册》中给出的平均修复时间模型[5]，该手册的模型表示多个相同单元同时检修的平均修复时间与检修1个失效单元的平均修复时间是相同的，这种观念的错误在于把随机变量的修复时间作为常数对待了。至于有限同时检修模型，迄今为止仍未见此类模型问世，笔者也给出了相应的模型[5]。

附带指出，商榷论文对修复概率与修复率不加区分，并令故障检测率、故障隔离率和修复率的乘积等于修复概率，这也是不适宜的。修复概率是在规定的时间内修复故障的概率，而修复率是指在单位时间内能够修复故障的次数，两者的量纲是不同的。修复率通常包含故障检测、故障隔离、拆卸、重装、检测和调整因素在内，并把这些因素占用的平均时间相加，作为平均修复时间。商榷论文中令故障检测率与故障隔离率这两个比例参数和修复率参数三者的乘积等于修复概率，但实际上，无论将这一乘积作为修复概率，还是作为修复率，都是不合适的。

最后，备件保障是修复失效单元的必要条件之一。没有备件保障，定期检修体制将无法实现，但是，商榷论文却没有考虑备件保障问题。

3　对商榷论文中给出的仿真数据的探讨

在商榷论文所给出的仿真示例中，系统由1 000个相同的单元组成，其中，要求保持900个单元正常工作，其他100个单元容许失效，这是1 000中取900的表决结构模型。单个单元的平均工作时间是20 000 h。

通过商榷论文中给出的仿真方法得到的MTBCF数据如表1所示。

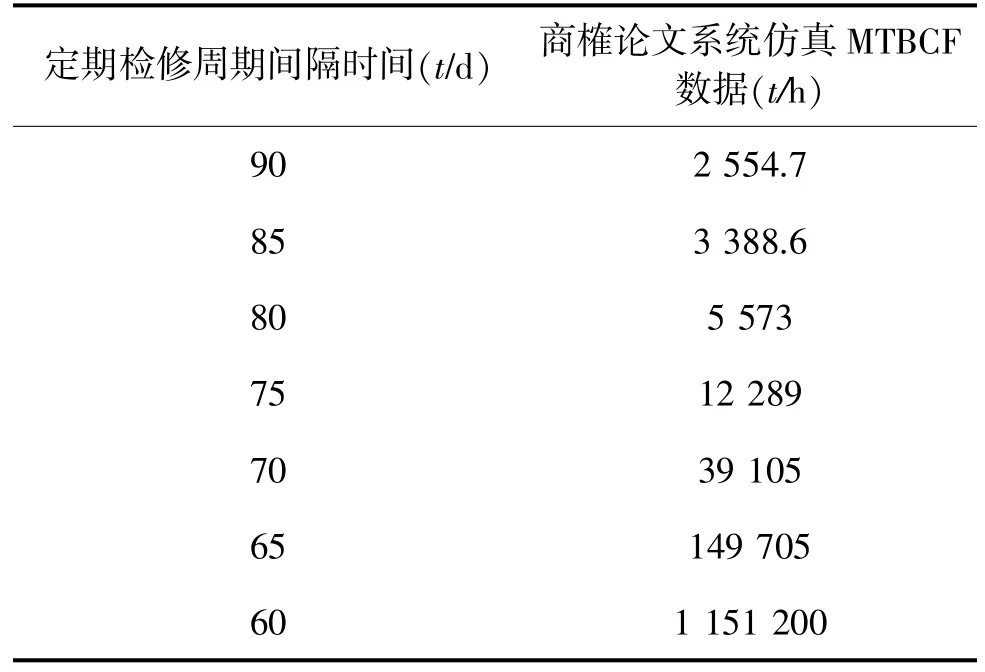
表1　商榷论文系统仿真MTBCF数据

从表1中第1行的数据可以看出，定期检修周期为90 d的系统的MTBCF为2 554.7 h。但实际上这是不可能出现的，因为在此周期内已经平均有102个单元发生了失效，而系统必须保持900个单元处于工作状态，这就是说，90 d的定期检修周期是不容许的。

下面证明一下所给出的相应定期检修周期内的平均失效数的依据。

在起始状态，由于平均工作时间为20 000 h的1 000个单元处于同时工作状态，所以第1次发生单元失效的时间是平均经过20 h，原因是在此状态下，系统的平均寿命是20 000 h除以1 000个工作单元，即20 h；第2次又发生1个单元失效的平均时间是20 000 h除以999个工作单元，即20.020 020 02 h；依此类推，把每次平均失效时间和失效数相加，就得到了累计时间为2 160 h、失效单元数为102个。

用相同的方法，可以得到其他6个定期检修周期的平均失效单元数。

用人工手算的方式相加，上述过程还是比较繁琐，但是，如果能够编制一个简单的计算程序，就可以快速地得到上述的结果。

下面我们再以表1中定期检修周期为60天、MTBCF为1 151 200 h等数据为依据，反推在此条件下失效单元的修复率和检修方式，得到的结果是单元的修复率等于0.682 875/h，检修方式为逐个地进行检修。

在此检修条件下，再计算其他定期检修周期下系统的MTBCF，得到的结果如表2所示。

表2　笔者得到的系统的MTBCF数值

下面将对表2中定期检修周期为90、85天的两组数据进行分析。通过上述讨论及表2中的数据可以看出，将90天作为周期是不能采用的，因为此时系统的MTBCF为2 128 h，实际上就是停机检修状态的MTBCF。85天检修周期的数据是通过利用定期检修周期为60天反推得到的失效单元的检修方式和检修能力数据得到的，此时，在检修时间内系统的累计失效单元达到了103个，系统已进入失效状态，因此，在此维修条件下，85天检修周期也是不能采用的。

当修复率为0.941 192/h且检修方式为同时检修时，要求MTBCF达到35 000 h，在定期检修周期为70天的条件下，冗余单元的数量可以大大地减少，但要补充备件保障设计。

4　建造定期检修解析模型的途径

建造此类定期检修的解析模型时，首先，要确立定期检修周期的界限，以保证系统不进入失效期；然后，在此基础上确定后续周期的工作时间，以使系统达到要求的MTBCF水平，这取决于3个必备的条件，即保持初始工作状态的条件、修复已经发生失效单元的条件和失效更换模块备件得到保障的条件。

如何利用解析式表达初始状态、上述3个必备的条件和状态的持续与衰退同步发生直到状态终止的整个过程，这就是定期检修的设计模型需要解决的问题。对此，我们将另文导出。

5　结束语

定期检修模型的提出，是可靠性理论模型研究中的一个突破，因为原来在可靠性经典研究中只存在停机检修和联机检修的两类模型，而在实际的工程中许多系统均需要通过定期检修的方式来检修。解决了定期检修方式的理论模型，是对实际工程可靠性设计的重要贡献。

实际上，定期检修模型是设计无人值守系统使用可用度的最佳途径，因此，除了应关注MTBCF参数外，还需注意系统的平均停机时间，包括平均修复时间、平均备件延误时间和平均停机预防维修时间[6]。

此外，对于可靠性、维修性和保障性的数字仿真更要谨慎，必须对仿真设计模型的客观符合性进行仔细推敲[7]，因为此类仿真结果没法通过仪器、仪表来验证，只能进行试验来验证。但是，对可靠性、维修性和保障性的定量试验验证，在要求相当的置信度条件下，通常需要的时间和费用均难以让人接受。对于仿真结果可用仪器、仪表验证的场合，数字仿真能发挥重要的作用，因为错误的数字仿真很容易被仪器、仪表检测结果所否定。

[1]丁定浩.联机检修的冗余结构使用可用度模型修正 [J].电子产品可靠性与环境试验，2012，30（5）：1-5.

[2]丁定浩.可靠性与维修性工程 [M].北京：北京电子工业出版社，1986.

[3]丁定浩.系统可靠性结构模型的新进展 [J].电子学报，1988，16（5）：110-112.

[4]胡宁，张三娣，黄永进.定期检修系统的可靠性建模与仿真 [J].电子产品可靠性环境试验，2014，32（2）：22-26.

[5]丁定浩，陆军.维修时间新参数和维修性设计新进展[J].中国电子科学研究院学报，2010，5（4）：391-384，388.

[6]丁定浩.装备寿命周期使用保障的理论模型与设计技术[M].北京：北京电子工业出版社，2011.

[7]丁定浩.可靠性数字仿真结果的作用、局限和陷阱的防范 [J].电子产品可靠性与环境试验，2007，25（6）：4-5.

Discussion on“Reliability Modeling and Simulation of Systems Periodically Maintained”

DING Ding-hao

The reliability analytical model and simulation block diagram of systems periodically maintained under continuous working state are given in the discussed article，but the maintenance mode and repair capacity of failure units are not involved and the service ability is not considered in the article，so it can't correctly reflect the objective process.And the unreasonable places are describled through an example，hoping to attract some attention of relevant personnel.

system periodically maintained；reliability analytical model；digital simulation；continuous working state；intermittent working state

TB 114.33;TP 391.92

A

1672-5468（2016）04-0001-04

10.3969/j.issn.1672-5468.2016.04.001

2015-05-05

丁定浩 （1929-），男，江苏吴江人，中国电子科技集团公司电子科学研究院研究员，上海大学、南京航空航天大学兼职教授，长期从事系统可靠性、维修性、保障性理论和工程设计研究工作。ddh_ddh@126.com