基于SUFI-2方法的SWAT模型在淮河息县流域月径流模拟中的应用

程海洲，余丽华

(宁波弘泰水利信息科技有限公司，浙江 宁波 315192)



基于SUFI-2方法的SWAT模型在淮河息县流域月径流模拟中的应用

程海洲，余丽华

(宁波弘泰水利信息科技有限公司，浙江 宁波 315192)

通过对模型输入参数进行不确定性分析，确定模型关键性参数和不确定性来源，对于提高模型率定效率和改进模型结构具有重要意义。通过应用SWAT分布式水文模型对息县流域1980—1995年的月径流过程进行模拟，同时基于SUFI-2算法进行模型参数敏感性分析、率定验证以及不确定性分析。结果表明：率定期与验证期的相关性系数R2和模型效率系数ENS均高于0.7，月径流量模拟值与实测流量过程线拟合程度较好；验证期小于率定期，模型不确定性较小；SUFI-2算法能够较好地分析SWAT模型参数的不确定性。

SUFI-2算法；SWAT模型；径流模拟

近年来，分布式水文模型越来越多地用于为洪水频发、土地利用变化和气候变化以及环境污染严重地区提供科学的决策依据[1]。20世纪90年代，在美国农业部(USDA)农业研究中心(ARS)Jeff Arnold博士的主持下，在吸取CREAMS、GLEAMS、EPIC、SWRRB等模型优点的基础上，将SWRRB和ROTO整合为一个新的模型[2-3]，即SWAT。其后，该模型开始广泛应用于径流模拟[4-7]、水质模拟[7-9]、土地覆被变化的影响评估[10-11]、气候变化的影响评估[11]等科学研究及实际应用中。通过以上资料可知，基于物理过程的分布式水文模型SWAT能够很好地分析出复杂大流域上土地管理措施对水、土/沙、营养物及农化物等的影响。由于分布式水文模型在模拟水文过程时需使用到大量的参数，因此，如何对这些参数进行率定并进行合理的不确定性分析就显得尤为重要。许多学者已针对这一问题采取过许多不同的研究方法[12-16]，本文使用由Abbaspour等人开发的SWAT-CUP中的SUFI-2算法对SWAT模型进行率定及不确定性分析。

1 研究方法

1.1 SWAT模型

SWAT模型是一个具有很强物理机制的分布式流域水文模型，在具有不同的土壤类型、不同的土地利用方式和管理条件下的复杂流域、资料缺乏地区，以及干燥、湿润或介于两者之间的气候条件下，对多种不同的水文物理过程，都能取得令人满意的模拟结果[17]。

SWAT模型是以研究流域的数字高程模型为基础，提取坡度、坡向、坡长、流向、河网和流域边界等流域特征信息，综合利用土壤类型、土地植被类型、土地利用等的空间数据，将流域离散化为不同的子流域以至水文响应单元(HRU)；再以HRU为空间计算单位，对流域的产流、坡面汇流、河道汇流等进行分析计算，并将运算结果汇集于流域出口。根据水文循环原理，SWAT模型的水量平衡基本表达式为：

(1)

式中：SWt为期末的土壤含水率(mm)；SW0为土壤初始含水率(mm)；t为时间(d)；Rday为第i天的降水量(mm)；Qsurf为第i天的地表径流(mm)；Ea为第i天的蒸发量(mm)；Wseep为第i天侧向渗流量(mm)；Qgw为第i天的垂向地下水出流量(mm)。

SWAT模型中，计算地表径流有2种方法：SCS径流曲线数法[18]、Green-Ampt模型法[19]，本文选取SCS曲线法计算地表径流；计算潜在蒸散发有3种方法：Hargreaves[20]、Penman-Montieth[21]、Priestly-Taylor[22]，本文因缺少实测太阳辐射数据，而Hargreaves方法不需要太阳辐射数据，故选取该方法计算潜在蒸散发。

1.2 SUFI-2算法

SUFI-2[23](Sequential Uncertainty Fitting，ver.2)是1种参数估计最优化方法，能够考虑模型结构、输入数据、模型参数等因素对模型计算的不确定性影响。它采用拉丁超立方随机采样方法取得参数值，带入模型运行摸拟，再计算目标函数值，并用P因子和R因子表示模型的不确定性程度[24]。P因子用95PPU表示，表示模拟的数据包括了95%的不确定性，剔除了5%的极坏模拟情况；R因子表示95PPU的上下限的平均距离与标准偏差的取值；P因子的范围为0～1，R因子的范围为0～∞，当P因子和R因子分别为1和0时表示模拟结果和实测数据一致。

在SUFI-2方法[25]中，敏感性矩阵和参数协方差矩阵的计算公式为：

(2)

(3)

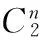
参数bj的95%置信区间通过中的对角元素计算得到：

(4)

而SUFI-2方法采用的评估模型不确定性程度的P因子和R因子的计算公式为：

(5)

在SUFI-2算法计算中，通常先假设一个比较大的参数区间，使得实测数据能够被包含在95PPU范围内，然后再结合模型运行结果逐步缩小区间范围，每一次参数范围的改变，都重新计算敏感性矩阵和协方差矩阵，并更新参数范围，进行下一步模拟，循环往复直至模拟值与实测值基本达到一致。根据SUFI-2算法，模型结果由一组模型参数决定，因此能最大程度地反映模型输入参数的不确定性。

2 应用研究

2.1 研究区概况

淮河流域地处我国东部，介于长江和黄河两流域之间，位于东经111°55′～121°25′，北纬30°55′～36°36′，面积为27万km2。息县位于淮河上游、河南省东南部、信阳市东北部，地形以低平的平原和缓丘为主，呈西北向东南略为倾斜，平均海拔47.00 m。淮河横贯全境，境内流长75.5 km，面积为920.97 km2，最低高程为39.00 m，最高高程为957.00 m，平均高程为141.30 m。气候属亚热带向暖温带过渡形气候，年平均气温15.2 ℃，年平均降雨量为946 mm，全年无霜期200 d左右。流域内主要土壤类型为水稻土和黄褐土，另外还有粗骨土、黄棕壤土和灰潮土等。流域土地利用/土地覆被的空间分布具有明显的地形和地域的差异。其主要类型以农田为主，占流域面积的46.8%；其次是林地和稻米，分别占18.95%和18.79%。息县素有天下第一县之称，是我国重要的农业生产基地。近年来，由于气候变化及农业耕作方式的改变，使得该地区的水循环特征发生了明显的改变。

2.2 基础资料库建立

SWAT模型所需的数据有DEM、土壤类型、土地利用、气象数据、降水数据、蒸发数据、控制站点流量资料等，相关数据的参数类别及数据来源见表1。

表1 SWAT模型输入数据表

在数据准备阶段，空间数据必须具有相同的投影格式和坐标系统，同时需要定义空间数据的投影。基于研究面积和区域，本文采用GCS_WGS_1984坐标系，Transverse_Mercator投影，中央子午线为111°。其次，本文应用ArcGIS的Archydro Tools模块对鄞江流域的DEM数据(见图1a)进行分析处理，包括洼地填充、流向分析、流量累积网格计算，并通过设定集水面积阀值自动提取数字河网，划分集水区域，获得44个子流域(见图1b)。根据不同土地利用(见图1c)和土壤类型(见图1d)的组合，在每一个子流域内进一步划分水文响应单元HRUs，划分为309个HRUs。

(a)DEM图

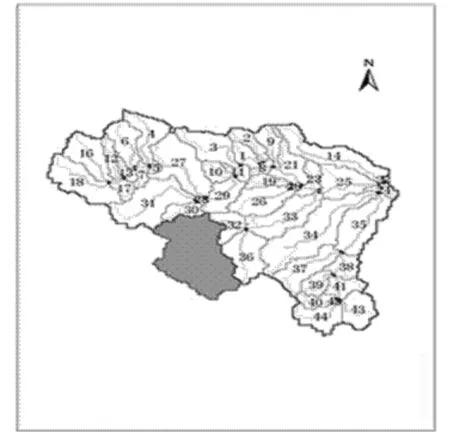
(b)子流域划分图

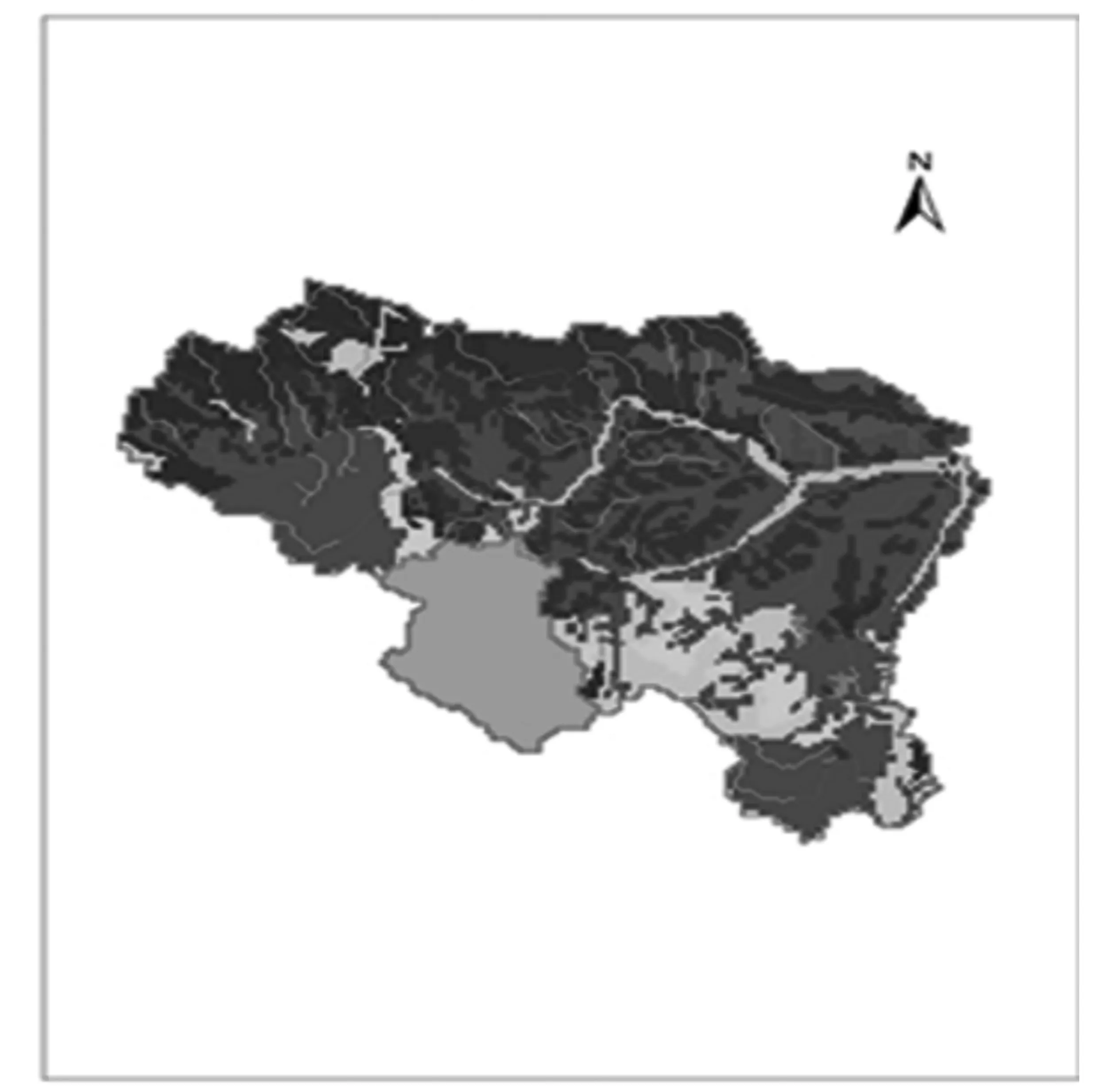
(c)1∶20万土壤类型图

(d)1∶20万土地利用图图1 研究区域的数字地图

3 结果分析

3.1 参数敏感性分析

SWAT模型参数众多，有的参数对模型模拟结果影响较小，有的参数细微变化对模型模拟结果有举足轻重的作用。因此，在采用SUFI-2方法进行参数不确定性分析之前，首先需要选出敏感性较强的模型参数，并对参数范围进行校正。本文使用SWAT模型自带的拉丁超立方随机抽样LH-OAT方法，对与径流有关的26个参数进行敏感性分析，表2列出等级前10的参数，以及这些参数的物理意义及初始范围。

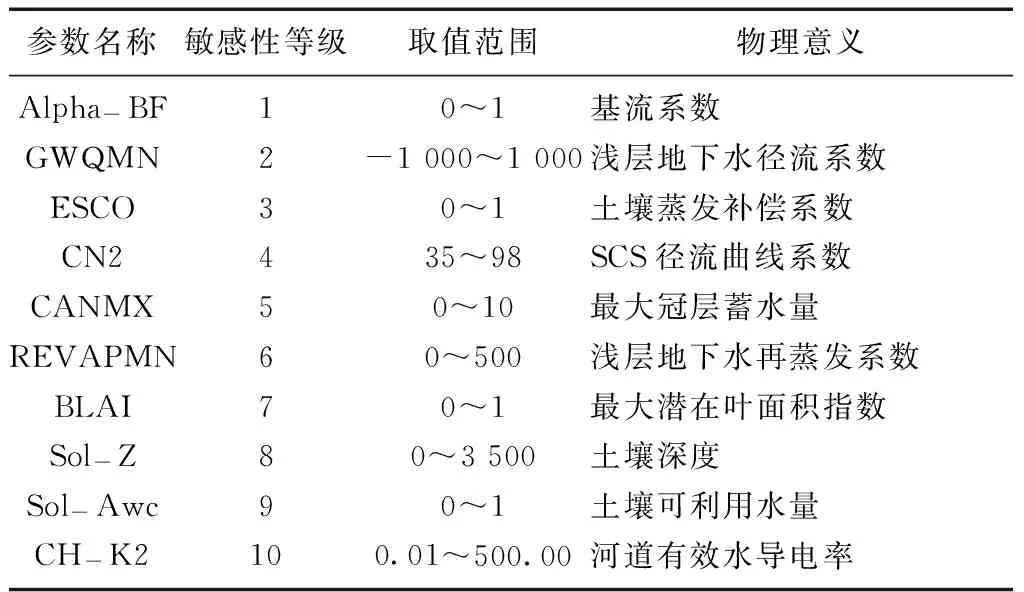
表2 参数敏感性排名表

在模型率定的过程中仅考虑这些敏感的参数，其余的参数对径流的模拟并没有显著的影响，故其改变不会对模拟效果产生显著的改变。

3.2 不确定性分析

根据选定的参数范围，利用SUFI-2方法对研究区域模型输入参数进行不确定性分析，模型目标函数采用观测值和模拟值间的相关系数(R2)和Nash-Sutcliffe效率系数(NSE)，以便综合评价SWAT模型的模拟效果：

(6)

(7)

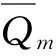
本文选取1980年作为预热年，1981—1990年为率定期，1991—1995年作为验证期；先对模型进行人工率定，使得模拟值与观测值间的差值减小，之后再使用SUFI-2算法对模型进行率定及不确定性分析。其中，人工调整的参数主要有基流系数(Alpha-Bf)、土壤蒸发补偿系数(Esco)、径流曲线系数(CN)、土壤可利用水量(Sol-AWC)。人工调参虽然很费时，但却有助于提高自动率定的精度。

3.2.1 率定期不确定性分析

文献[1]模拟12 a日径流数据时，设置SUFI-2算法模拟次数为2 000次，模拟效果较好。本文模拟11 a月径流数据，模拟次数设置为1 000次，通过将模拟数据与实测数据进行对比发现，模拟结果具有较高的相关系数(R2)和Nash-Sutcliffe系数(NSE)。同时，根据Moriasi[26]提出的模型计算评价标准：若R2>0.7，NSE>0.5，就认为模拟效果满意。本文的模拟结果满足要求，表3列出了率定期月径流模拟的评价。图2列出了率定期月径流量实测值和模拟值。

表3 率定期月径流模拟评价因子表

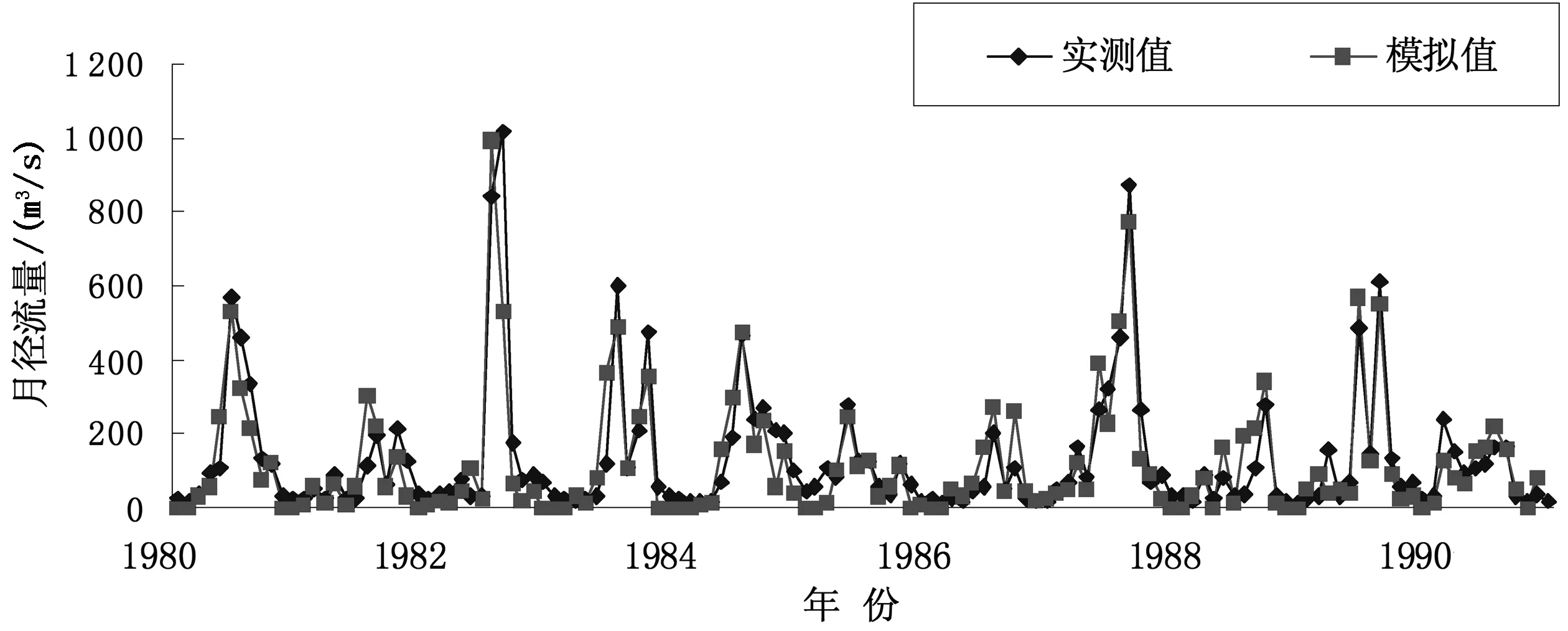
图2 率定期月径流量实测值和模拟值图

由表3看出，虽然率定期R2为0.85，NSE为0.82，r-因子0.67，说明模拟结果令人满意，但P-因子只达到0.28。P-因子是95%预测不确定性(95PPU)范围内实测数据的百分比，0.28说明仅有28%的实测数据落在95PPU范围内，说明模型的不确定程度较高。原因可能是输入数据如降雨、温度等的不准确，上游水库放水等。

表4列出了结合人工率定及用SUFI-2算法率定后的敏感性参数最适值及范围，这些参数值在SWAT模型中已加以修改，以便于进行下一步的模型验证及对流域进行其他方面的研究。

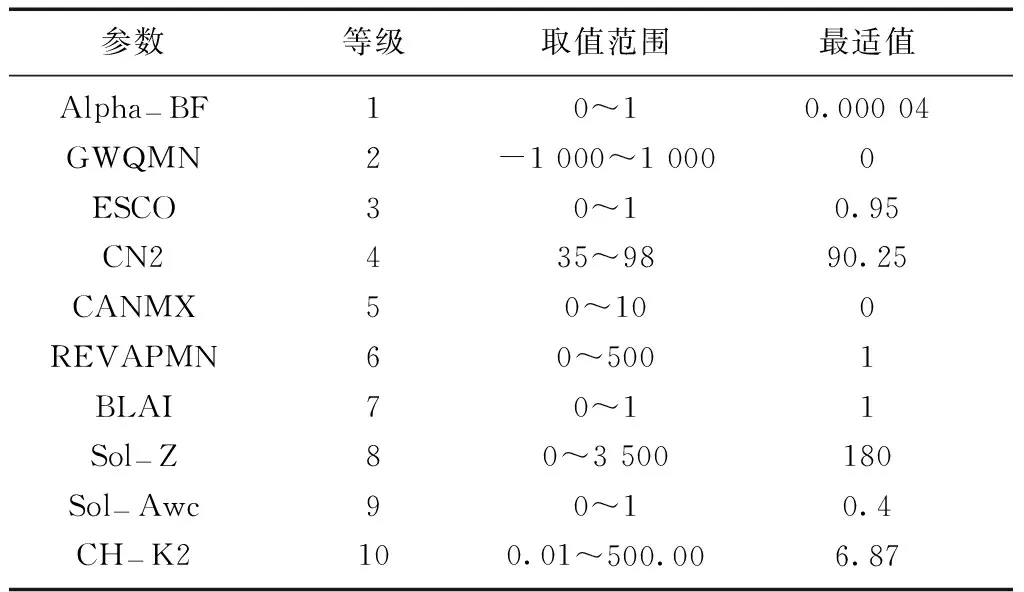
表4 SWAT径流敏感参数及最适值表

3.2.2 验证期不确定性分析

由表3看出，验证期1991—1995年R2为0.73，NSE为0.71，R-因子0.65，由于率定期P-因子较低，故验证期P-因子0.26也较低。图3列出了验证期径流量实测值和模拟值，可看出模拟效果较好，由验证期率定得的参数能够很好地代表流域及其产汇流的特征，故而模型能够在今后对流域的研究中起到重要作用。

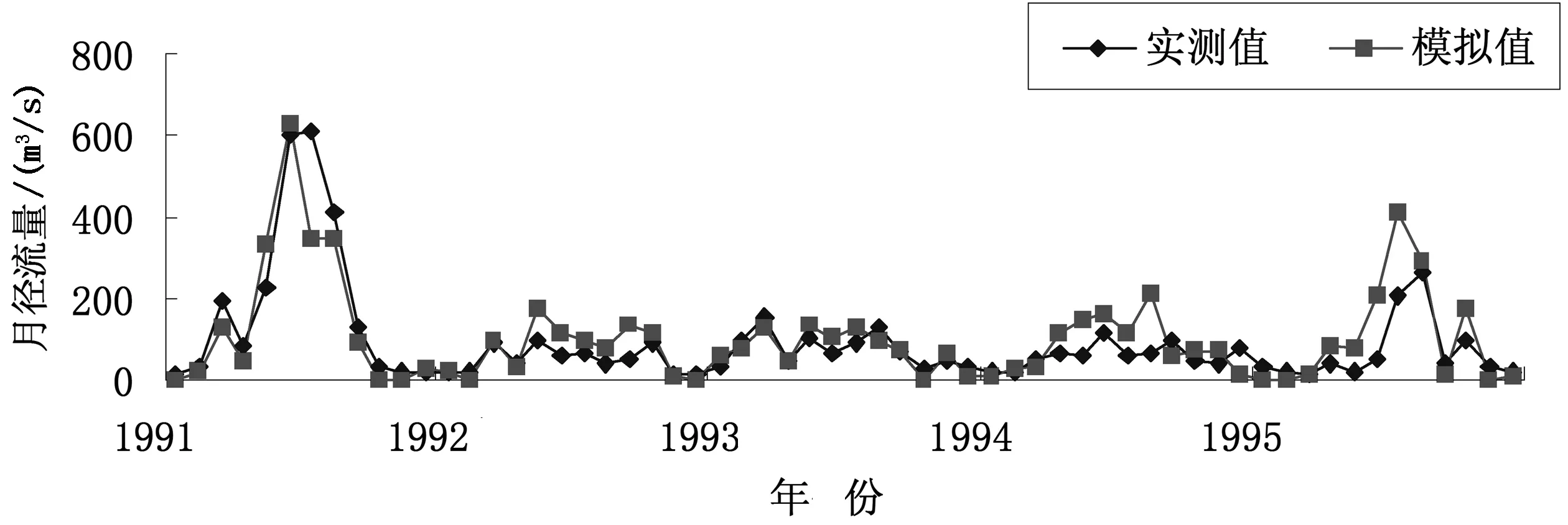
图3 验证期月径流量实测值和模拟值图

4 结 论

本文利用淮河息县流域的DEM、土壤类型、土地利用、水文气象等资料，应用SWAT模型对该流域的1980—1995年16 a的月径流过程进行模拟，并采用SUFI-2算法对模型参数进行率定验证和不确定性分析，主要结论如下：

(1)应用SWAT模型进行的月径流模拟在率定期和验证期都能取得比较满意的模拟结果，其中，月径流量率定期NES为0.82，R2为0.85，验证期NES为0.71，R2为0.73，表明SWAT模型在研究区域具有较好的适用性。

(2)参数敏感性分析结果表明，与径流有关的26个参数中，Alpha-BF、GWQMN、ESCO、CN2、CANMX等对径流模拟结果影响最为显著。

(3)不确定性分析结果显示，率定期和验证期的P-因子分别为0.28和0.26，表明SWAT模型在研究区域的月径流模拟中具有较高的不确定性。

(4)采用SUFI-2方法得到的参数组，可以取得较好的模拟效果，表现在较高的NSE值和值。

(5)率定期及验证期径流模拟结果曲线图显示出良好的模拟效果，验证了SUFI-2方法可以较好的应用于SWAT摸型不确定性分析之中。

(6)综合考虑率定期和验证期的模拟结果，可知在人工调参的基础上对SWAT模型采用SWATCUP中SUFI-2算法进行率定能达到较高的模拟精度。

[1]Shimeils G.Setegn，Ragahavan Srinivasan，Bijian Dargahi.Hydrological modelling in the Lake Tana Basin，Ethiopia using SWAT model[J].The Open Hydrology Journal，2008(2):49-62.

[2]张银辉.SWAT模型及其应用研究进展[J].地理科学进展，2005，24(5):121-130.

[3]王中根,刘昌明,黄友波.SWAT模型的原理、结构及应用研究[J].地理科学进展，2003，22(1):79-86.

[4]Arnold J G and Allen P M.Estimating hydrologic budgets for three Illinois watersheds[J].Journal of Hydrology，1996，176(1/2/3/4):57-77.

[5]Arnold J G，Srinivasan R，Muttiah R S，Allen P M.Continental scale simulation of the hydrologic balance[J].Journal of the American Water Resources Association，1999，35(5):1037-1051.

[6]Eckhardt K and Arnold J G.Automatic calibration of a distributed catchment model[J].Journal of Hydrology，2001，251(1/2):103-109.

[7]Vassilios Pisinaras，Christos Petalas，Georgios D.Gikas，et al.Hyrologyical and water quality modeling in a medium-sized basin using the Soil and Water Assessment Tool[J].Desalination，2010，250(1):274-286.

[8]Debele B，Srinivasan R，Yves Parlange J.Coupling upland watershed and downstream waterbody hydrodynamic and water quality models(SWAT and CE-QUAL-W2)for better water resources management in complex river basins[J].Environ Model Assess，2008，13(1):135-153.

[9]Abbaspour KC，Yang J，Maximov I，et al.Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT[J].Journal of Hydrology，2007，333(2/3/4):413-430.

[10]胥彦玲,王苏舰,李怀恩.土地覆被变化对流域非点源污染的影响[J].水土保持研究，2010，17(3):250-253.

[11]张圣微,雷玉平,姚琴.等.土地覆被和气候变化对拉萨河流域径流量的影响[J].水资源保护，2010，26(2):39-44.

[12]C.H.Green and A.van Griensven.Autocalibration in hydrologic modeling:Using SWAT2005 in small-scale watersheds[J].Environmental Modelling & Software，2008，23(4):422-434.

[13]A.van Griensven，T Meixner，S.Grunwald，et al.A global sensitivity analysis tool for the parameters of multi-variable catchment models[J].Journal of Hydrology，2006，324(1/2/3/4):10-23.

[14]Zhang Li，Zongxue Xu，Quanxi Shao，et al.Parameter estimation and uncertainty analysis of SWAT model in upper reaches of the Heihe river basin[J].Hydrological Processes，2009，23(19):2744-2753.

[15]秦富仓,张丽娟,余新晓,等.SWAT模型自动校准模块在云州水库流域参数率定研究[J].水土保持研究，2010，17(2):86-89.

[16]朱丽,秦富仓,姚云峰,等.SWAT模型灵敏性分析模块在中尺度流域的应用[J].水土保持研究，2011，18(1):161-165.

[17]Vanliew M W and Garbrecht J.Hydrologic simulation of the Little Washita River Experimental Watershed using SWAT[J].Journal of the American water resource association，2003，39(2):413-426.

[18]USDA.Urban Hydrology for small watersheds[R].Engineering Division，Soil Conversation Service，USDA，Technical Release 55，1986.

[19]Green W H ，Ampt G A.Studies on Soil Physics，1.The Flow of Air and Water through Soils[J].Journal of Agricultural Sciences，1981(4)：1-24.

[20]Hargreaves，G.L.；Hargreaves，G.H.；Riley，J.P.:Agricultural benefits for Senegal River Basin[J].Journal of Irrigation and Drainage Engineering，1985，111(2):113-124.

[21]Penman．H．L．Evaporation：An introductory survey[J]．Netherlands Journal of Agricultural Science，1956(4)：7-29．

[22]Priestley C.H.B.and Taylor R.J.On the assessment of surface heat flux and evaporation using large-scale parameters[J].Month.Wea.Rev，1972，(100)：81-92.

[23]Abbaspour KC，Johnson CA，van Genuchten MT.Estimating uncertain flow and transport parameters using a sequential uncertainty fitting procedure[J].Vadose Zone Journal，2004，3(4):1340-1352.

[24]魏丹,刘智勇,李小冰.SWAT模型及SUFI-2算法在秃尾河上游流域径流模拟中的应用[J].干旱地区农业研究，2013，30(6):200-206.

[25]Gupta，H.V’,S.Sorooshian,P.O.Yapo.Toward improved calibration of hydrologic models:Multiple and noncommensurable measures of information[J].Water Resources Research，1998，34(4):751-763.

[26]Moriasi DN，Arnold JG，Van Liew MW，Binger RL，Harmel RD,Veith T.Model evaluation guidelines for systematic quantification of accuracy in watershed simulations[J].Transactions of the ASABE，2007，50(3):885-900.

(责任编辑 姚小槐)

2015-06-06

程海洲(1983-)，男，工程师，硕士，主要从事水文水资源模型及水利信息化研究。

E-mail:chenghzhyun@126.com

TV121

B

1008-701X(2016)01-0061-05

10.13641/j.cnki.33-1162/tv.2016.01.019