“勾股定理”中的数学思想

杨翠芹

“勾股定理”中的数学思想

杨翠芹

email：czsshy@126.com

请在每题后的直线上填出该例运用了何种数学思想.

【例1】已知一个直角三角形的两边长分别为3和4，求第三边长.

【点评】在题目没有指明斜边、直角边的情况下，要先确定斜边、直角边.

本例运用了（填数学思想）.

【例2】已知，如图，折叠长方形的一边AD使点D落在BC边的点F处，已知AB=8cm，BC= 10 cm，求ED的长.

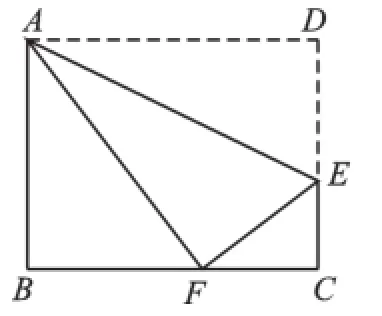
【分析】先求出BF、CF，再设EF=ED=x，则CE=8-x,在Rt△CEF中可根据勾股定理列方程.

解：∵四边形ABCD是矩形，∴CD=AB=8，AD=BC=10，∠B=∠C=90°，∵△AEF由△AED折叠得到的，∴△AEF≌△AED，AF=AD=10, EF=ED，在Rt△ABF中，由勾股定理得：BF=CF=BC-BF=10-6=4，设EF= ED=x，则CE=8-x，在Rt△CEF中，由勾股定理得：42+（8-x）2=x2，∴x=5，即ED=5.

【点评】折叠问题的本质是轴对称（全等性、对称性），要找出隐含的折叠前后的位置关系和数量关系，然后再应用勾股定理列方程.

本例运用了（填数学思想）.

【例3】如图，用硬纸板做成了两个全等的直角三角形，两直角边的长分别为a和b，斜边长为c，又做了一个以c为直角边的等腰直角三角形，你能将它们拼成一个能证明勾股定理的图形吗？（1）如果能，请你画出拼好的示意图，写出它是什么图形？（2）用这个图形证明勾股定理．（3）假设有若干个两直角边的长分别为a和b的直角三角形，你能运用它们拼出其他能证明勾股定理的图形吗？如果能，请画出拼后的示意图．（无需证明）

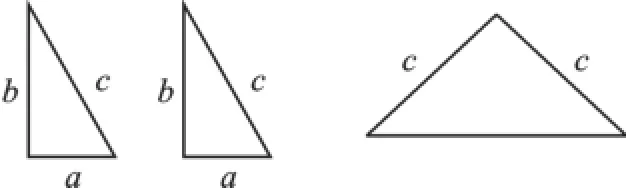
【分析】勾股定理的证明要运用拼图法来做，以形求数，数形结合.

（1）解：如图，可拼成直角梯形.

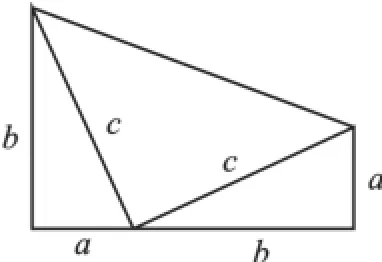
（2）证明：∵S梯形=2×（a+b）（a+b），∴（a+b）（a+b），即a2+b2=c2.

（3）解：可以，所拼图形如下：

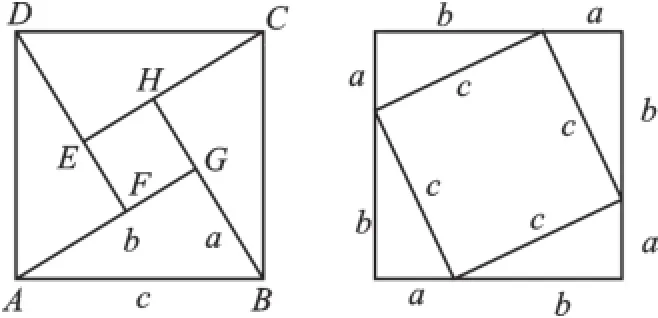
【点评】这道题关键要熟练掌握课本勾股定理证明涉及的几种常见的图形以及证明过程和等面积法，抓住思想.

【例4】如图有两棵树，一棵高7米，另一棵高2米，两树相距24米，一只小鸟从一棵树的树梢飞到另一棵树的树梢，至少飞了多少米？

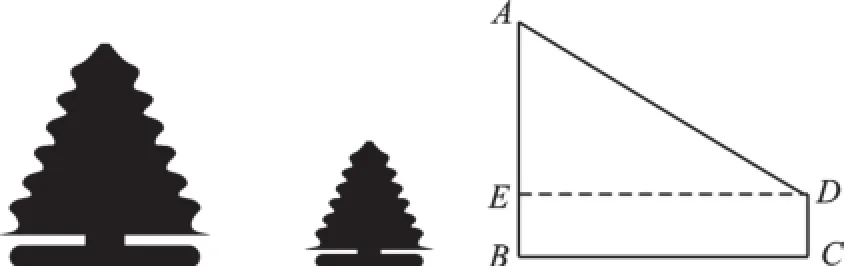
【分析】首先要把实际问题化为包含直角三角形的数学问题，再联系图形直接用勾股定理解答.

解：由题意得AE=7-2=5，DE=24，在Rt△ AED中，由勾股定理得AD=

答：小鸟至少飞了25米.

【点评】解答勾股定理的实际应用题，首先要审清题意，然后找出试题情景中涉及的直角三角形，再结合勾股定理便可以求出了.

本例运用了（填数学思想）.

【例5】如图，在等腰△ABC中，∠ACB=90°，D、E为斜边AB上的点，且∠DCE=45°.

求证：DE2=AD2+BE2.

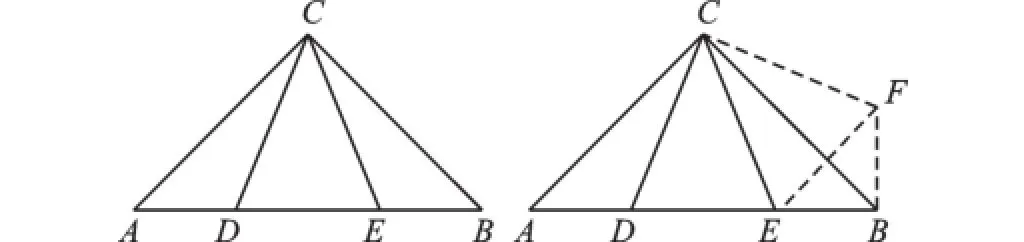
【分析】要证明三边的关系，就要将边转移到一个三角形中，可以通过旋转构造直角三角形，运用勾股定理.

证明：把△ACD绕点C逆时针旋转90°得△BCF，则△ACD≌△BCF，BF=AD,CF=CD,∠CBF=∠CAD=45°,∠DCF=90°.∵∠DCF=90°,∠DCE=45°,∴∠DCE=∠FCE=45°，∵CF=CD,∠DCE=∠FCE=45°,CE=CE，∴△CDE≌△CFE，∴FE=DE，∵在等腰△ABC中，∠ACB=90°，∴∠CBA=45°，∴∠EBF=∠CBA+∠CBF=90°，在Rt△EBF中，由勾股定理得：FE2=BF2+BE2，∵FE=DE,BF=AD，∴DE2=AD2+BE2.

【点评】勾股定理是求线段关系的一种很重要的方法,若图形缺少直角条件,可通过作辅助垂线的方法,构造直角三角形.这题关键要利用旋转变换，将三边转移到一个三角形中，并构造直角三角形.

本例运用了（填数学思想）.

（作者单位：江苏省常州市武进区雪堰初级中学）

责任编辑：沈红艳见习编辑：李诗