采用改进粒子群算法的修正弹脉冲参数优化建模与仿真
李 嘉,唐恩凌,胡晓阳,纪雪松
(1.沈阳理工大学 装备工程学院,沈阳 110159;2.辽沈工业集团有限公司 研发中心,沈阳 110045)
采用改进粒子群算法的修正弹脉冲参数优化建模与仿真
李 嘉1,2,唐恩凌1,胡晓阳1,纪雪松2
(1.沈阳理工大学 装备工程学院,沈阳 110159;2.辽沈工业集团有限公司 研发中心,沈阳 110045)
为提高脉冲修正弹药的末段修正控制效果,对其脉冲参数的优化设计问题进行研究。针对脉冲修正弹药脉冲离散控制的特点,建立了脉冲修正弹道模型,提出了一种脉冲控制策略,以弹目落点偏差最小为第一优化目标、以消耗脉冲总冲最小为次优目标,在一定约束条件下建立了脉冲参数优化数学模型,应用改进粒子群算法对脉冲参数进行了优化。数值计算结果表明,基于改进粒子群算法的脉冲参数优化设计数学模型具有较快的收敛性,利用该优化方法获得的脉冲参数,按照设计的修正控制策略,能够获得较佳的修正控制效果。
脉冲修正弹药;改进粒子群算法;脉冲参数;控制策略;优化设计
为提高常规武器弹药的命中精度,基于脉冲直接侧向力的弹道修正技术已成为常规武器弹药智能化研究的重点,如美国和俄罗斯等国家均采用脉冲直接侧向力控制技术研制出了120毫米激光半主动末修迫弹。在实现脉冲修正弹药的研究中,弹药的总体结构与气动布局设计、脉冲修正弹道模型、控制方案与控制策略、脉冲参数设计等均是一些重要问题。从目前国内研究情况看,主要集中在脉冲控制力的特点、脉冲修正弹道模型的建立及脉冲控制弹道特性分析、脉冲控制策略与点火条件、脉冲发动机的数量与点火相位优化等方面进行了大量研究。文献[1]详细阐述了与气动控制力相比,脉冲控制力的特点等;文献[2-4]建立了基于脉冲控制的飞行弹道数学模型,并分析了脉冲个数、脉冲力大小、脉冲作用时间、布置位置与弹丸转速等参数对末段弹道修正能力和弹道特性的影响规律;文献[5]设计了一种脉冲修正控制导引律,阐述了脉冲发动机的点火条件等;文献[6]基于蒙特卡洛法对脉冲发动机的数量与冲量进行了优化;文献[7]以所需脉冲发动机数量最小为目标函数,对点火相位进行了优化设计。本文针对脉冲修正弹药的离散性特点,设计了一种脉冲控制策略,以弹目落点偏差R最小为第一优化目标,以消耗脉冲总冲IT最小为次优目标,提出了一种基于改进粒子群算法的脉冲参数优化设计方法,为脉冲修正弹药的脉冲参数设计提供参考。
1 脉冲修正弹道模型
脉冲修正就是利用布置在弹体表面周向特定位置上的一系列微型推力器(通常为脉冲式固体火箭发动机),通过喷口垂直或偏转一定角度向外喷射燃气流,凭借喷流的反作用力为制导弹药提供控制力和力矩,以改变制导弹药的位置和飞行姿态,实现弹道修正的目的。脉冲修正具有如下特点[1]:(1)脉冲控制力和力矩的作用时间短;(2)脉冲发动机的能量有限,提供的控制力有限;(3)不能够连续作用,具有离散性。这些决定了脉冲修正弹药采用的控制策略、脉冲参数优化方法等有其自身的特点。为了能够对脉冲参数进行优化设计,首先需建立脉冲修正弹药的飞行弹道模型。
与常规未修正弹药相比,脉冲修正弹药在飞行弹道末段增加脉冲发动机的推力作用,因而在建立外弹道模型时,首先需获得脉冲控制力及控制力矩。选取文献[8]中的弹体坐标系、弹轴坐标系和速度坐标系对脉冲控制力及控制力矩进行描述。设γ为滚转角,γp为作用脉冲发动机沿顺时针方向相对于弹体坐标系Oy1轴的夹角,则脉冲控制力及控制力矩在第一弹轴系三轴上的投影为
(1)
(2)
式中
(3)
式中:Fpξ、Fpη、Fpζ和Mpξ、Mpη、Mpζ为脉冲控制力和脉冲控制力矩分别在第一弹轴系三轴上的投影分量;Fp为脉冲控制力,当无脉冲工作时为0;Ip为脉冲冲量;tk为单脉冲点火时间;τ为单脉冲持续作用时间;Lp为脉冲控制力的作用点与弹体质心间的距离,作用点位于质心与弹头之间时为正。
将脉冲控制力在第一弹轴系三轴上的分量转换至速度坐标系O-x2y2z2的三轴上,得到
(4)
式中,δ1、δ2为高低攻角与侧向攻角;αa为第二弹轴系Oη′轴与第一弹轴系Oη轴之间的夹角。
将脉冲发动机的控制力(式(4))和力矩(式(2))及常规未修正弹药所受的作用力和力矩分别投影到速度坐标系和第一弹轴坐标系的各轴上,由牛顿第二定律和动量矩定律即可得到脉冲修正弹药的六自由度外弹道方程组为
(5)
式中,Fx2、Fy2、Fz2为无脉冲作用时作用在弹丸上的合力在速度坐标系上的投影;Mξ、Mη、Mζ为无脉冲作用时作用在弹丸上的合力矩在第一弹轴坐标系上的投影。上述合力、合力矩的具体表达式及方程组中各符号的意义参见文献[8]。
2 脉冲控制策略
根据脉冲修正弹药脉冲离散控制的特点,脉冲发动机需逐个旋转到修正方位范围内才能起修正作用,且脉冲发动机作用后,由于其作用时间短、作用力大,使得弹体摆动变化剧烈,不利于后续探测弹道参数的准确获取与修正决策等。为此,本文采用在弹道末段适时位置处根据实际探测弹道参数与方案弹道参数间的偏差,一次决策、形成对应该探测弹道参数偏差的匹配作用脉冲个数,按等脉冲间隔方式选取相应脉冲发动机作用的串行控制策略。
3 脉冲参数优化数学模型
基于脉冲修正弹药的弹道修正原理,为了提高弹道修正效果,通常希望在弹体周向布置尽可能多的小型脉冲发动机,且单个脉冲发动机的冲量不要过大。但在弹药总体设计过程中,考虑到弹体的空间体积、结构强度、抗高动态发射环境,及其未修正弹药的散布特性等,脉冲发动机的个数、单脉冲冲量、决策起修时间和弹体转速等参数存在着较优的匹配组合。
3.1 优化设计变量与目标函数

脉冲修正弹药是一类精确制导弹药,它追求对目标的圆概率误差CEP尽可能小,为此,本文以弹目落点偏差R最小为第一优化目标,以消耗脉冲总冲IT最小为次优目标,通过引入权重系数λ1和λ2(λ1、λ2为正数,且λ1+λ2= 1),构造的目标函数为
(6)
式中,弹目落点偏差R为弹丸落点坐标(xc,zc)与目标坐标(xm,zm)间的距离,其表达式为
(7)
3.2 约束条件
约束条件是对设计变量的取值给予某些限制的数学关系式,或是对优化设计问题本身提出一些条件限制,是使设计方案在满足这些限制条件下达到较优。对于脉冲修正弹药设计参数优化模型,参加调优的设计方案需满足如下约束条件。
(1)脉冲发动机个数及单脉冲冲量约束
对于脉冲修正弹药,若干小型脉冲发动机沿弹体周向均匀布置,由于弹体空间尺寸有限及其结构强度的限制,脉冲发动机的个数只能为有限个,取其约束为nmin≤n≤nmax(n为整数)。单脉冲发动机的冲量与火药类型、装药量等有关,取单脉冲冲量约束为Iimpmin (2)起修时间约束 起修时间越早,脉冲具有的修正能力越大,但由于重力的影响,导引头测试误差会变大,同时也会受到导引头的视场角和探测距离等的影响;起修时间晚,有利于系统各项误差的累积,导引头测试数据的精度也会提高,但脉冲具有的修正能力会减小。因此,脉冲修正弹药通常在弹道的末段进行修正,其起修时间约束为tqmin≤tq≤tqmax。 (3)弹体转速约束和脉冲点火时间间隔约束 (4)稳定性约束 对于设计稳定的脉冲修正弹药,脉冲控制作用后,仍必须满足其追随稳定性和动态稳定性,即修正飞行过程中的攻角幅值不能超过一定的限制,即δ≤δmax。 (5)修正能力约束 脉冲修正弹药在弹道末段需具有一定的修正能力,需与其需求修正能力Xd相适配,Xd值可通过对弹箭未修正散布或目标运动特性的分析予以确定。本文取修正能力Xa的约束为Xa≥Xd。 3.3 优化设计模型 综上所述,脉冲修正弹药的参数优化设计模型为 (8) 式中,E5表示关于设计变量的5维欧氏空间,gi(x)表示优化模型中的不等式约束。 优化问题式(8)为有约束混合整数非线性规划问题,这类问题中的设计变量既有连续变量又有整数离散变量,且约束的存在要求寻优时不仅要使目标函数不断趋于极值,还要求实时检验解的可行性,因而其求解过程比一般有约束优化问题复杂得多。本文拟采用基于自适应罚函数的改进粒子群算法对优化设计模型(8)进行寻优。 粒子群算法是根据模拟鸟群觅食过程中的迁徙和群集现象,提出的一种用于解决优化问题的群智能算法[9]。求解过程为首先初始化为一群随机粒子(随机解),然后通过迭代寻得最优解。在每一次迭代中,粒子通过跟踪2个极值来更新自己,一个是粒子本身所找到的最优解称为个体极值,另一个是整个种群目前找到的最优解称为全局极值。 在D维的目标搜索空间中,设s为群体中的粒子数,f为由被优化函数决定的适应值,xi(t)为粒子i迭代t次后的位置,vi(t)为粒子i迭代t次后的速度,pi(t)为粒子i迭代t次后所找到的个体极值,g(t)为迭代t次后整个种群所找到的全局极值。在每次迭代过程中,每个粒子的更新速度和位置为 vi(t+1)=wvi(t)+c1r1(pi(t)-xi(t))+ c2r2(g(t)-xi(t)) (9) xi(t+1)=xi(t)+vi(t+1) (10) 式中:w为惯性权重;c1、c2为加速系数(也称学习因子);r1、r2为[0,1]之间均匀分布的随机数。 4.1 自适应罚函数的构造 对于有约束的优化设计问题通常采用罚函数法将有约束问题转换为无约束问题进行求解,其中,自适应罚函数法[10]能够利用寻优过程中的反馈信息动态地调整罚因子,其寻优效果较佳。为此,本文利用群体的目标函数平均值及个体的违反约束程度,提出了一种带有自适应惩罚函数的改进粒子群算法。 (11) 式中,m为约束的个数,wj(Xi)表示粒子Xi对第j个约束函数的违反值,其表达式为 (12) (13) 对于不可行粒子,上述惩罚函数将充分结合个体和群体的适应值信息与约束违反情况动态地调节惩罚强度。 4.2 取整操作策略 在脉冲修正弹药参数优化设计问题中,脉冲个数n只能为整数,因此要求粒子中整数变量位置的更新是在整数空间内进行。根据式(9)可更新粒子的速度,由于c1、c2和r1、r2的存在,即使粒子的位置和速度均为整数,下一个位置粒子的速度还有可能是实数,由式(10)可知粒子的位置也不可能为整数,这样使得搜索实际上是在实数空间中进行的,不能保证在整数空间内进行更新,因此需进行取整操作。本文采用一种简单、可行的随机取整方法来解决粒子更新中的整数变量问题。 设整数变量在实数空间搜索更新时的数值为r,取整时将从相邻的两个整数floor(r)和ceil(r)中随机选择,floor(r)、ceil(r)分别表示向下和向上取整,而被选概率与它们到r的距离成反比。若以Int(r)表示对r的取整操作,则有 (14) 式中U(0,1)是[0,1]上均匀分布的随机数。 以某脉冲末修迫弹为算例进行弹道计算分析,根据该弹的弹道环境条件和未修正散布特性等,其主要计算条件为:初速390m/s,射角45°,单脉冲持续作用时间30ms,脉冲发动机布置在弹体质心处。优化设计变量取值范围为:脉冲发动机个数6~12,单脉冲冲量30~50N·s,起修时间36~42s,弹体转速2~8r/min,脉冲点火时间间隔60~150ms,攻角幅值限制δmax=6°,弹道需求修正能力约束Xd=80m。 采用上述算法进行优化时,取粒子总数s=45,目标搜索空间维数D=5,随机生成的邻域拓扑结构中最多有4个粒子,惯性权重w=0.8,加速系数c1=c2=1.54,目标函数权重系数λ1=0.7、λ2=0.3。在相同计算条件下对优化程序进行10次试验,每次试验的最大迭代代数设为200。 由表1可知,由于粒子群算法属于一种随机优化方法,多次寻优结果略有差异,表现出了随机特性,但总体上看,多次优化的最优目标函数值的变化均较小。从图1单次粒子群优化过程来看,最优目标函数值在迭代初期下降较快,随着粒子的不断进化,其降低变得缓慢,当粒子的进化代数为30时,已趋于一定值,表明改进粒子群算法的脉冲参数优化设计数学模型具有较快的收敛性和较好的优化效果。 表1 脉冲末修迫弹脉冲参数优化模型的求解结果(10次) 图1 优化迭代过程中最优目标函数值的收敛曲线 利用优化设计的脉冲参数和六自由度弹道模型,应用蒙特卡洛模拟打靶法对其修正控制效果进行计算分析。计算中考虑初速、弹重、阻力系数、纵风与横风或然误差分别为1.5m/s、40g、0.5%、1m/s;脉冲发动机总冲、工作时间、作用方位的偏差分别为±2.5N.s、±4.5ms和±5°,弹目偏差角测量偏差±0.5°。 图2给出该末修迫弹算例在未修正与修正条件下的弹道落点散布情况(模拟打靶100次),由图2可知,经过脉冲发动机修正后弹药的落点的横向和纵向密集度都显著提高,表明采用该优化方法获得的脉冲参数,按照设计的修正控制策略,能够获得较佳的修正控制效果。 图2 未修正和修正条件下的弹道落点散布 基于脉冲修正弹药脉冲离散作用进行弹道修正的特点,设计了一种脉冲控制策略,研究了脉冲修正弹药的脉冲参数优化问题,利用改进粒子群算法对脉冲参数进行了优化设计。以某脉冲末修迫弹为算例,在设定的弹道初始条件和约束条件下,数值计算获得一组较优的脉冲参数,单次粒子群优化过程表明,基于改进粒子群算法的脉冲参数优化设计数学模型具有较快的收敛性。利用获得的优化脉冲参数对该脉冲末修迫弹进行了弹道修正控制,其落点的横向和纵向密集度都显著提高,表明采用该优化方法获得的脉冲参数,按照设计的修正控制策略,能够获得较佳的修正控制效果,该方法对脉冲修正弹药的脉冲参数设计是可行的。 [1]宋锦武,祁载康,夏群力.简易制导脉冲控制力修正技术研究[J].北京理工大学学报,2004,24(5):383-386. [2]曹小兵,王中原,史金光.末制导迫弹脉冲控制建模与仿真[J].弹道学报,2006,18 (4):76-79. [3]易文俊,王中原.基于脉冲控制的末段修正弹道研究[J].南京理工大学学报,2007,31 (2):219-223. [4]曹小兵,王中原.末段脉冲修正迫弹攻击区建模与仿真[J].系统仿真学报,2009,21 (17):5399-5402. [5]张成.脉冲修正弹药射程预测控制方法[J].弹道学报,2010,22 (1):20-23. [6]王佳伟,霍鹏飞,陈超.基于蒙特卡洛法的冲推器数量与冲量优化[J].探测与控制学报,2010,32 (1):92-96. [7]曹营军,杨树兴,李杏军.基于脉冲控制的末段弹道修正弹点火相位优化研究[J].兵工学报,2008,29(8):897-901. [8]韩子鹏.弹箭外弹道学[M].北京:北京理工大学出版社,2008. [9]Parsopoulos K E,Vrahatis M N.Particle Swarm Optimization and Intelligence:Advances and Applications [M].Hershey,PA:Information Science Reference,2010. [10]Barbosa H J C,Lemonge A C C.An adaptive penalty method for genetic algorithms in constrained optimization problems[J].Frontiers in Evolutionary Robotics,I-Tech Education Publ.,Austria,2008. (责任编辑:马金发) Research on Optimal Method of Impulse Parameters Using Modified Particle Swarm Optimization LI Jia1,2,TANG Enling1,HU Xiaoyang1,JI Xuesong2 (1.Shenyang Ligong University,Shenyang 110159,China;2.Liao-Shen Industrial Group Co.,Ltd.,Shenyang 110045,China ) In order to improve terminal trajectory correction control effect of the impulse correction ammunition,the optimal design of the impulse parameters was studied.Aiming to the characteristics of impulse discrete control,the impulse correction trajectory model is established and an impulse control strategy is proposed.The minimum falling point deflection between projectile and target and the minimum total impulse are considered as the first optimal and sub-optimal objective function respectively,an optimal design model of impulse parameters is established under certain constraint conditions.The impulse parameters are optimized using modified Particle Swarm Optimization.The numerical results show that optimal design mathematical model of impulse parameters based on modified Particle Swarm Optimization has a faster convergence,a better correction control effect can be obtained through the use of impulse optimal parameters obtained by the optimal method and the correction control strategy designed in the paper. impulse correction ammunition;modified particle swarm optimization;impulse parameters;control strategy;optimal design 2015-11-11 李嘉(1983—),男,工程师,研究方向:弹箭飞行理论与控制技术。 1003-1251(2016)04-0062-06 TJ012.3 A
4 改进粒子群优化算法

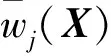

5 数值计算分析




6 结束语

