一种模糊K-means算法在测试用例集约简中的应用

余国清， 周兰蓉， 罗可

(1. 长沙理工大学 计算机与通信工程学院， 湖南 长沙 410114；2. 湖南信息职业技术学院 计算机工程学院， 湖南 长沙 410200)



一种模糊K-means算法在测试用例集约简中的应用

余国清1,2， 周兰蓉2， 罗可1

(1. 长沙理工大学 计算机与通信工程学院， 湖南 长沙 410114；2. 湖南信息职业技术学院 计算机工程学院， 湖南 长沙 410200)

为了提高软件测试用例集约简的成效，提出一种基于模糊K-means的软件测试集用例约简算法，引入模糊划分思想，结合测试需求集，从各个簇中抽取测试用例，尽可能地发现相似的用例.实验结果表明：算法能够最小化约简用例集，用例集覆盖范围最广泛，错误率检测较高.

用例约简; 模糊K-means算法; 复杂度; 软件测试

随着互联网、云计算等技术的快速发展，软件功能及规模也迅速增大，程序开发潜在的错误和漏洞也逐渐增多[1-3].软件测试可以在软件开发完成之后，使用控制数据、加工数据等用例进行测试，发现软件存在的错误，保证软件的完整性、可靠性和准确性.但是，大规模软件需要设计较多的测试用例，造成人工测试模式定位难度大、耗费时间较长，不能够快速定位和修改软件错误[4-5].软件测试用例约简已经成为降低软件测试用例数量和提高测试成效的关键技术，许多学者对其进行了研究[6-11]，引入了集合约简、关联规则、专家数据库等技术，在保持较高测试准确度的条件下，大大减少了用例数量.软件测试用例约简仍存在用例集规模较大、用例重复出现、错误定位精确度小等问题.本文引入隶属度函数改进K-means算法，旨在利用模糊数学提高软件测试用例划分的准确度.

1 背景理论

1.1 软件测试用例约简

测试用例需要全覆盖软件的每一个步骤和环节，针对每一行代码进行测试.软件测试用例约简是指在用例集T中，寻找一个最简化的子集T′，该子集可以满足所有的测试任务.

1.2 模糊K-means算法

K-means算法采用硬聚类划分思想，划分过程较为武断，不能够充分地考虑测试用例的多个属性，导致聚类结果与实际情况存在偏差.因此，为了能够提高K-means算法的准确度，假设软件测试用例共有n个，每一个测试用例使用m个特征进行刻画，则引入了隶属度函数，使用隶属度刻画测试用例归属，提高数据对象划分准确性，易于解释和描述．软件测试用例为

(1)

式(1)中：xi，j表示样本j的特征i，j=1,2,…,n，i=1,2,…,m.为了能够更好的保证K-means算法正确执行，算法运行之前需要对其检修归一化处理，即

(2)

式(2)中： xi，max表示第i个指标特征的最大取值；xi，min表示第i个指标特征的最小取值；ri，j表示归一化后xi，j的取值.软件测试用例集矩阵X归一化之后为

(3)

软件测试用例集X假设存在C个类别，则数据集X可以使用模糊识别矩阵进行描述，即

(4)

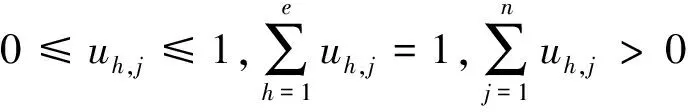
假设软件测试样本划分类别h的m个特征向量值作为K-means算法的中心数据，则一个具有X个类别的软件测试用例集拥有C个模糊聚类中心，即

(5)

式(5)中：si，h为类别h指标i的归一化特征值，0≤si，h≤1.

为了满足不同的聚类用户处理需求，在模糊聚类执行过程中，可以针对不同的划分设置不同的特征权值，以便能够突出某些特征属性的贡献度，即

(6)

模糊K-means算法的目标函数形式为

(7)

2 在测试用例机约简中的应用

在模糊K-means算法中，假设软件测试用例集为T={t1,t2,…,tn}，数据集拥有的类别数目为K个，mi为第i个簇的中心，i=1,2,…k.模糊K-means的目标函数为

(8)

式(8)中：b为一个常数，可以控制模糊K-means隶属度.通过对模糊K-means的隶属度函数求导数，可以获取模糊K-means算法的最优解，最优解的求解过程分别为

(9)

(10)

模糊K-means算法使用程序，迭代执行最优化求解式(9)，(10)，可以针对软件测试用例集进行划分.具体的算法伪代码流程如下.算法输入：软件测试用例约简类簇数目K，隶属度控制常数参数b，N个数据对象的软件测试用例集.算法输出：软件测试用例约简后的K个簇.算法有以下4个步骤.

步骤1 随机化的将N个软件测试用例分配到K个簇中，分派每一个簇的中心特征向量为mi.

步骤2 使用式(10)准确计算获取软件测试用例的隶属度函数.

步骤3 使用式(9)重新计算软件测试用例簇的中心值mi.

步骤4 计算每一个数据对象的隶属度，直到隶属度不再变化，终止算法运行；否则，返回步骤2.

由于在K-means算法基础上，引入模糊控制b，可以根据模糊控制因子的取值经验.当b=0.75时，能够取得较好的约简效果.基于此，可以分析测试用例的属性相近程度.

3 实验结果分析

3.1 数据集

采用SiemensCorporateResearch提供的软件测试公共数据集，数据集1,2,3包含的用例数为30；数据集4,5,6,7包含的用例数为32.

3.2 评价标准

约简算法的评价标准有算法约简率(SR)、软件错误检测率(FDE)、软件错误检测丢失率(FL)3个方法，分别表示为

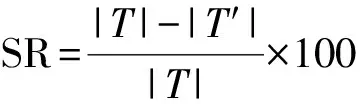
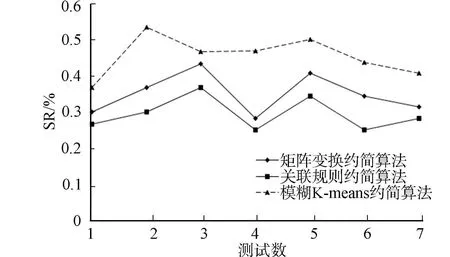
图1 3种算法约简率Fig.1 Three algorithms reduction rate

其中：|T|为软件测试用例集的元素数；|T′|为约简算法约简后的软件测试用例集中的元素数；|F|为未约简的用例集测试软件功能时检测出来的错误数；|F′|为约简后的用例集检测出来的软件功能错误数.

3.3 结果分析

1) 约简率比较.3种算法约简率，如图1所示.模糊K-means算法引入了模糊控制因子，可以动态地调整隶属度特征权重，将概率值较为接近的软件测试用例划分到一起，在保证全覆盖的条件下，可以有效提高K-means算法的约简率，降低软件测试的复杂度和工作量.

2) 软件错误检测率比较.3种算法检错率，如图2所示.模糊K均值算法约简后的测试用例能够检测出更多软件错误数，表明文中算法约简后的依然可以保持全覆盖能力.另外两种算法约简后，把一些测试功能不同的用例划分到一个簇中，这样造成约简后的用例无法全覆盖软件功能，错误检测率较低.

3) 错误检测丢失率比较.3种算法的错误检测丢失率，如图3所示.由图3可知：矩阵行列变换算法、关联模式约简算法非常容易将不同覆盖类型的用例约简掉，因此，漏检率较低，算法约简效果不好.

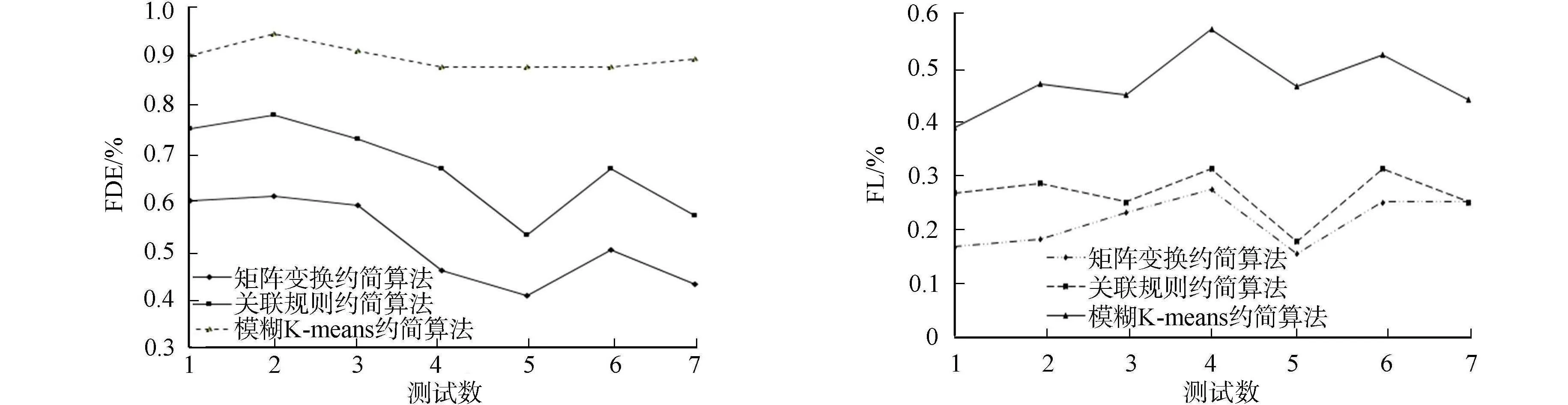
图2 3种算法检错率 图3 3种算法错误检测丢失率Fig.2 Three algorithms error rate Fig.3 Three algorithms error detection loss rate

4 结束语

在K-means算法中引入了隶属度函数，采用模糊数学思想提高K-means算法划分软件测试用例集，可以提高用例约简数量，并且保持用例集检测软件错误的可靠性.未来研究工作包括两个关键内容：引入模拟退火理论，实现模糊控制因子的自动化确定;针对软件测试用例集进行泛化，提高算法的稳定性和鲁棒性.

[1] KUMAR G,BHATIA P K.Software testing optimization through test suite reduction using fuzzy clustering[J].Csi Transactions on Ict,2013,1(3):253-260.

[2] PAKINAM N B,NAGWA L B,MOHAMED H,et al.Test case generation and test data extraction techniques[J].International Journal of Electrical and Computer Sciences,2011,24(5):112-119.

[3] SUN F,TONG X H,XUE S F.A study of relative redundancy in test-suite reduction while retaining or improving fault-localization effectiveness[C]∥Proceedings of the 2010 ACM Symposium on Applied Computing.[S.l.]:ACM,2010:2229-2236.

[4] HAO D,XIE T,ZHANG L,et al.Test input reduction for result inspection to facilitate fault localization[J].Automated Software Engineering,2010,17(1):5-31.

[5] GONG Hongfang,LI Junyi.Generating test cases of cluster-level based on classes dependencies reduction[J].Jouranl of Central South University: Science and Technology,2010,41(1):238-244.

[6] GU Qing,TANG Bao,CHEN Daoxu.A test suite reduction technique for partial coverage of test requirements[J].Chinese Journal of Computers,2011,34(5):879-888.

[7] CHEN Jing,YANG Meihong,WANG Lu,et al.Regression test case reduction model based on association mode[J].Computer Engineering,2011,37(2):63-65.

[8] ZHOU Chongbo,LOU Jungang,CHENG Long.Test suites reduction based on matrix transformation[J].Application Research of Computer,2013,30(3):779-782.

[9] CHEN Yangmei,DING Xiaoming.Test suite reduction methods based on K-medoids[J].Computer Science,2012,39(6):422-424.

[10] SU Xiaohong,GONG Dandan,WANG Tiantian,et al.Automatic fault localization approach combining test case reduction and joint dependency probabilistic model[J].Journal of Software,2014,25(7):1492-1504.

[11] 刘竹松,陈洁.考虑数据不确定性的非均匀挖掘算法[J].华侨大学学报(自然科学版),2016,37(3):308-311.

(责任编辑： 陈志贤 英文审校： 吴逢铁)

FuzzyK-Means Algorithm of Software Testing Using Case Reduction

YU Guoqing1,2, ZHOU Lanrong2, LUO Ke1

(1. Deptment of Computer and Communication Engineering,Changsha University of Science and Technology, Changsha 410114, China;2. School of Computer Engineering, Hunan College of Information Technology, Changsha 410200, China)

To improve the effectiveness of the software test set reduction, a software test set case reduction algorithm based on fuzzyKmeans is proposed. The fuzzy partition idea is introduced. The test suite is extracted from each cluster, finded similar cases. Experimental results showed that the algorithm can minimize the reduction case set, covers the most extensive and highly detect the error rate.

case reduction; fuzzyK-means software testing; complexity; software testing

10.11830/ISSN.1000-5013.201606024

2016-10-20

余国清(1971-)，男，副教授，主要从事人工智能、智能控制、数据挖掘的研究.E-mail:yuguoqing@mail.hniu.cn.

湖南省科学技术计划项目(2011FJ3086)

TP 311

A

1000-5013(2016)06-0778-04