基于阻抗法的悬挂器试压波动抑制技术

刘 均 ， 袁 峰

(1.东北石油大学电气信息工程学院 大庆, 163318) (2.哈尔滨工业大学电气工程与自动化学院 哈尔滨, 150001)



基于阻抗法的悬挂器试压波动抑制技术

刘 均1,2， 袁 峰2

(1.东北石油大学电气信息工程学院 大庆, 163318) (2.哈尔滨工业大学电气工程与自动化学院 哈尔滨, 150001)

以水击方程为基础，借鉴电路的阻抗分析方法，研究连续波动在管道中的传递特性。分析了外接管道对波动传递的影响，设计了用于滤除管道内特定频率波动的滤波器，推导出管道长度和滤波器尺寸与波动传递之间关系。通过实际应用发现，以阻抗理论为基础设计的滤波器能够很好地抑制泵压波动，提高试压过程的准确性和效率。

连续波动； 试压； 滤波器； 悬挂器

引 言

悬挂器是在固井过程中将尾管与上层套管联接起来的一种机械装置，用于将尾管座挂在上层套管的末端[1]。悬挂器悬挂动作的触发是由悬挂器内缸的压力决定的。当进行悬挂操作时，在地面注入钻井液进行蹩压，当钻井液压力增至额定压力时，剪断液压缸销钉，让悬挂器的内缸和外缸产生相对位移，从而带动卡瓦涨开，完成尾管的座挂[2-4]。为了让悬挂器正常工作，在悬挂器生产过程中需要通过试压技术确定悬挂器的工作压力。试压使用的试压泵一般为电动往复式柱塞泵，由电机驱动柱塞，带动滑块运动，将流体注入悬挂器液缸，当液缸销钉断裂时的压力就是悬挂器的工作压力。在试压过程中，由于试压泵的转速比较高，如果直接用管道将试压泵和液缸连接起来，由于柱塞的运动，在管道和液缸中会产生剧烈的压力波动，从而导致同样材质与尺寸的销钉测试结果相差很大。分析认为，这个误差是由压力剧烈变化造成的，因此为了减少测试时的误差，需要对管道和液缸内的压力波动进行抑制。

目前，国内外对于管道内压力波动的研究主要集中在水击波在管道中的传递和振荡过程，研究的是管道中压力突然改变后，压力脉冲的传递与衰减特性[5-11]。管道中连续波动的分析与计算主要集中在能量的分布和对振动信号的采集处理[12-13]。一般认为，管道对于波动信号类似于低通滤波器，低频信号衰减少，高频信号衰减多，但对如何抑制管道中特定频率的波动理论和方法较少涉及[14-18]。

笔者以水击方程为出发点，研究连续波动在管道内的传递机理，推导了利用传递矩阵描述管道内压力波的数学模型。基于传递矩阵设计了用于抑制压力波动的滤波器，解决了销钉剪切压力高速测量的问题。

1 管道内压力波动的矩阵模型

管道内单个压力波的传递可以用水击方程表示，该方程描述了当管道中阀门关闭后，管道中产生的单个压力波动在管道中的传递情况[16]。

(1)

其中：H为水头；V为流速，D为等效水力直径；β为管道与水平面的夹角；a为波速；f为与摩擦力相关的系数。

式(1)为典型的非线性双曲型偏微分方程组，有很多经典解法，但都为数值解。对于研究管道的频率响应特性，只有数值解是不够的。

(2)

其中：A为管道等效水力面积。

如果认为摩擦力的影响f不随时间和位置改变，将式(2)中的第1式对x求导，第2式对t求导后推出

(3)

其中：R=fQ/2gDA2为一常数。

如果管路一端试压泵运转时加载在管道中的压力波动形式为正弦波，则可求出式(3)的解为

(4)

其中：c1，c2为常数，与边界条件相关；ω为角频率；γ2=-(ω2+jAgωR)/a2；p(x)为压力波动的幅值。

由于a，A，R对于具体的管道可以认为是常量，那么γ只与角频率ω相关。将式(4)及其导数带入式(2)，可以求出

(5)

其中：q(x)为流量波动的幅值。

p(x)和q(x)为距离x的函数。对于具体的管道，γ只与角频率ω相关，可以将γ定义为管道流体传播常数。由于水压驱动了水分子的运动，电压是电子流动的动力，二者具有相似性，故可以模仿电路理论中阻抗的定义方式来定义管道对流体压力波动的阻抗为

(6)

Z(x)代表了管道对波动的阻力，在输电理论中，定义无限长输电线路的阻抗为特征阻抗，在管道中也可以定义管道的特征阻抗为Zc=ja2γ/gAω，它的物理含义是无限长管道对波动的阻力[19]。

对于长度为l的管道，如果知道了波动起始位置x=0处的压力振幅pi=p(0)和流量振幅qi=q(0)，根据式(4)和式(5)，就可以计算出c1和c2

可以将任意位置x处的压力振幅和流量振幅表示为

末端x=l处的压力振幅po可表示为

pisinh(γl)-Zcqicosh(γl)

(7)

同样，将末端x=l处的流量振幅qo表示为

(8)

将式(7)，(8)写成矩阵方式

(9)

当有不同管道串联时，在联接点处相当于一条管道的末端和另一条管道的始端相连，且联接点处压力振幅和流量振幅相等，因此联接点的方程为

连接点的传递矩阵为

(10)

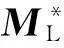
(11)

其中：ML1为第1条管道的传递矩阵；ML2为第2条管道的传递矩阵。

根据传递矩阵可以写出管道终端处压力振幅po和流量振幅qo与始端处压力振幅pi和流量振幅qi的关系

(12)

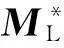
(13)

式(13)说明在负载确定的情况下，波动经过串联异径管道后振幅的变化情况。

2 管道的幅值频率特性

由于式(13)得到的是波动在管道入口和出口的幅值之比，说明了管道对波动的衰减情况。如果固定除波动的角频率ω(ω=2πf)之外的参数，可以绘制出管道对不同频率信号的响应曲线。对于长度分别为50m和200m的两根管道，如果取直径D=40mm，波速a=1 280 m，终端阻抗R0=3Zc，依据式(9)和式(13)计算出这两条管道的幅值频率特性曲线，如图1所示。可以看出，不同频率的信号通过管道后其衰减幅度是不一样的。当输入端波动信号的幅值pi一定时，输出端波动信号的幅值po随着信号频率的增加而呈现波动衰减，特别在低频部分会出现po远大于pi的情况，这是由于波动传递过程中的反射与叠加造成的。

图1 管道的幅值频率响应Fig.1 The amplitude frequency characteristic in pipeline

对于50m短管道来说，输入端的波动会完整地传递到输出端，衰减很小，在某些频段还会出现输出波动大于输入波动的情况，正是这种波动导致了测试误差。对于较长的管道，波动主要集中在低频区域，随着频率的上升，末端振幅的波动现象减少。

3 用于抑制管道中波动的滤波器

为了抑制管道中的波动，设计合适的管道结构用于改变管道的频率幅值特性，使试压泵工作时产生的波动信号衰减掉。由于泵工作时转速是一定的，设计的滤波器只需要滤除特定频率的信号即可。

管道的物理参数会影响波动的传递，设计如图2所示的管道结构。将传递压力的管道分为两段L1和L2，在L1和L2的连接部位安装一个储液罐L4，储液罐L4通过短管L3与L1和L2相连，储液罐L4为一圆柱形容器。设L1，L2，L3和L4的长度分别为l1，l2，l3和l4；L1，L2和L3的截面积均为A，L4的截面积A4远大于A。L1左端为波动输入端，输入的压力振幅为pi，流量振幅为qi；L2的右端为波动输出端，输出的压力振幅为po，流量振幅为qo；在L1，L2和L3的连接点P处，压力分别为p1，p2，p3，流量振幅分别为q1，q2，q3；在L4末端压力振幅为pm，流量振幅为qm。

图2 滤波器结构图Fig.2 Structure of the filter

由于在连接点P处压力连续，p1=p2=p3，q1=q2+q3，因此连接点处传递矩阵可以表示为

(14)

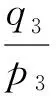
L3和L4串联后的矩阵传递表达式为

其中：pm和qm为L4末端的压力与流量振幅。

由于L4末端封闭，则qm=0，可以推导出(CL3AL4+DL3CL4)p3+(CL3BL4+DL3DL4)q3=0，最后计算出

(15)

由于L3较短，且处于L3和L4中的流体基本不流动，忽略分支管以及容器中的摩擦力，可以将传递系数和特征阻抗简化为γ=jω/a，Zc3=ρa/A3，Zc4=ρa/A4。根据双曲函数和三角函数的关系，将thγl简化为

从而得到

(16)

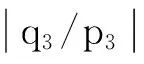
(17)

计算出L1左端的压力和流量波动与L2右端的压力和流量波动的关系为

(18)

根据式(13)和式(18)，得到带滤波器管道的幅值与频率的衰减特性。假设波速a为1 280m/s；L1，L2和L3具有相同的直径为20mm，长度分别为0.49，15.5和0.2m；容器L4的直径为200mm，长度l4为292mm。图3为此时管道的幅值频率特性。可以看出，加入滤波器后，管道的频率幅值特性与图1相比发生了改变。在30～60Hz和65～100Hz之间的振荡得到了较好抑制，但在某些频段振荡会加强，出现共振现象。例如，在60～65Hz之间振荡非常剧烈，此频率范围是整个管道的共振范围，需要避免使用此频率，否则会导致管道的损坏。根据参数计算出串联管道的谐振频率ωn为529 r/min，即84Hz。图3中，84Hz信号衰减是最大的，在谐振频率附近的信号也有很大衰减，可以利用滤波器的特性完成对泵压波动的滤除。

图3 带滤波器管道的幅值频率特性Fig.3 The amplitude frequency characteristics for the pipeline with filter

4 实验与应用

为了解决高速试压的需要，设计制作了用于测试悬挂器工作压力的测试装置，如图4所示。

图4 悬挂器试压装置Fig.4 The hanger pressure test device

测试装置由横放的悬挂器双层液缸、直径为20mm的快接管道、水泵、压力传感器和计算机系统组成。双层液缸分为内缸和外缸，内外缸通过销钉固定并密封。传感器测量范围在25MPa，精度为0.1%，采样频率为500Hz。在试压过程中，首先加工4只同尺寸销钉，取其中两只销钉安装到液缸上，然后对管道和液压缸注水并排气，由试压泵加压，缸内压力逐渐上升，直至销钉剪断为止。压力传感器记录销钉在断裂瞬间的压力值，这个值用于标记剩余两支销钉的剪切压力值，这个压力值就是悬挂器出厂后的触发压力值。

在测试装置中使用3柱塞泵，电机转速为950r/min，电机每旋转一周产生3个压力脉冲。管道内压力波动频率大约在48Hz左右，在不使用滤波器，直接将泵的输出通过管道接入液缸时，管道和悬挂器内的压力波动很剧烈，给测试过程带来很大误差，测试时的压力波形如图5所示。对于同批次加工的同型号销钉，多次测量的结果相差很大，从测量的压力曲线来看，销钉断裂的瞬间，压力值可以出现在波峰和波谷之间的任意位置。对同批次销钉进行多次测试，计算测试结果的平均值，用参与计算的单次测量值与平均值比较可以发现，单次测量值都偏离平均值，最大测量值和最小测量值之差超过1MPa，且多次测量的结果没有规律性，故可以认为测量误差很大，数据不可信。

图5 不使用滤波器时悬挂器内压力变化Fig.5 Pressure changes in the hanger without filter

在距离试压泵0.5m处加入直径为200mm，长度为292mm的滤波器后，压力传感器测量到的管道中压力波动如图6所示。可以看出，管道中压力波动明显减小，压力的上升比较平缓，同批次销钉多次测量后的最大测量值与最小测量值之差小于0.2MPa，这个误差处于可接受的范围，因此认为滤波器能有效滤除泵压的波动，解决了销钉剪切压力高速测量的问题。

图6 使用滤波器后管道内压力变化Fig.6 Pressure changes in the hanger with filter

不同速度的泵由于转速不同，在管道内产生的波动信号频率也不同，需要根据具体的信号频率设计滤波器的尺寸。另外，在实验中要注意滤波器中的空气。当滤波器容器中混入空气时，由于空气有很高的压缩比，会改变滤波器的谐振频率，导致滤波性能不好。最好的解决办法是将滤波器处于管道下方，让滤波器内部的空气自然排出。

5 结 论

1) 利用阻抗法描述连续压力波动在管道中的传递情况，可以将管道材质和流体特性等因素用阻抗和传递系数简单地表示出来。

2) 用矩阵模型描述连续波动信号在管道中的传递特性，适用于分析各种复杂结构管道中连续波动的传递。

3) 在直管道中，当连续的压力波动产生后，不同频率的信号传递距离是不一样的。随着频率的增加，管道出口处压力振幅呈现周期性衰减，总体趋势为低频衰减小，高频衰减大。

4) 在管道中安装滤波器后，滤波器改变了管道的频率响应，适当的设计能有效减少管道中的压力波动。不同形状的滤波器会带来不同的频率响应特性，本研究涉及的模型适用于圆柱体滤波器，其他形状滤波器的滤波特性需要进一步研究。

[1] 马开华, 朱德武, 马兰荣. 国外深井尾管悬挂器技术研究新进展[J]. 石油钻探技术, 2005, 33(5): 52-55.

Ma Kaihua, Zhu Dewu, Ma Lanrong. Advances in liner hanger techniques in deep wells outside China[J]. Petroleum Drilling Techniques, 2005, 33(5): 52-55. (in Chinese)

[2] Lohoefer C L, Mathis B, Brisco D. Expandable liner hanger provides cost-effective alternative solution[C]∥IADC/SPE Drilling Conference. New Orleans, Louisiana: Society of Petroleum Engineers, 2000:1-12.

[3] Nida R, Meijs R, Reedd S. Innovative expandable liner-hanger application saves time on pinedale anticline drilling operations: two case studies[C]∥SPE Annual Technical Conference and Exhibition. Houston,Texas: Society of Petroleum Engineers, 2004:1-8.

[4] 吴柳根, 马建忠, 宁学涛. 膨胀悬挂器技术在石油工程中的应用[J]. 石油矿场机械, 2012, 41(9): 59-63.

Wu Liugen, Ma Jianzhong, Ning Xuetao. Expandable liner hanger technology applied in petoleum engineering[J]. Oil Field Equipment, 2012, 41(9): 59-63. (in Chinese)

[5] 胡荣霞, 李金海. 泵系统中水锤与阀控制的研究综述[J]. 水利科技与经济, 2006, 12(12): 816-818.

Hu Rongxia, Li Jinhai. Research review of water hammer and valve control in pump systems[J]. Water Conservancy Science and Technology and Economy, 2006, 12(12): 816-818. (in Chinese)

[6] 曹慧哲, 贺志宏, 何钟怡. 有压管道水击波动过程及优化控制的解析研究[J]. 工程力学, 2008, 25(6): 22-26.

Cao Huizhe, He Zhihong, He Zhongyi. The analytic research on the wave process and optimal control of water hammer in pipes[J]. Eegineering Mechanics, 2008, 25(6): 22-26.(in Chinese)

[7] Ghidaoui M S, Zhao Ming, McInnis D A. A review of water hammer theory and practice[J]. Applied Mechanics Reviews, ASME, 2005, 58(1): 49-76.

[8] Wang Jianxun, Liu Huijin. A time-frequency mixed method for on-line monitoring of harmonics and interharmonics[C]∥2011 International Conference on Advanced Power System Automation and Protection. Beijing: IEEE, 2011: 228-233.

[9] Liu Ronghui, Yang Erbin, Yang Xiu. Analysis of transient harmonics in power systems based on wavelet packet transform[C]∥The 3rd International Conference on Power Electronics and Intelligent Transportation System. Shenzhen: International Institute of Tropical Agriculture Association, 2011: 345-348.

[10]Jameson A. Time dependent calculations using multigrid, with applications to unsteady flow past airfoils and wings[J]. AIAA Journal, 1991, 6: 1591-1596.

[11]Boucher R F, Kitsiors E E. Simulation of fluid network dynamics by transmission line modeling[J]. Joumal of Mechanical Engineering Science, 1986, 92(3): 97-111.

[12]朱显明, 张国良, 黄其柏, 等. 均匀流管自由振动的能量分布特征[J]. 振动、测试与诊断, 1999, 19(2): 98-100.

Zhu Xianming, Zhang Guoliang, Huang Qibai, et al.Characteristics of free vibration energy distribution in a pipe filled with uniformly flowing fluid[J]. Journal of Vibration, Measurtment & Diagnosis, 1999, 19(2): 98-100. (in Chinese)

[13]谷立臣, 闫小乐, 刘泽华. 小波变换的流体压力信号自适应滤波方法研究[J]. 振动、测试与诊断, 2009, 29(2): 205-208.

Gu Lichen, Yan Xiaole, Liu Zehua. Adaptive filtering method for fluid pressure by using wavelet transform[J]. Journal of Vibration, Measurtment & Diagnosis, 2009, 29(2): 205-208.(in Chinese)

[14]刘修善, 苏义脑. 钻井液脉冲信号的传输特性分析[J]. 石油钻采工艺, 2000, 22(4): 8-10.

Liu Xiushan, Su Yinao. Investigation on the transmission behaviors of drilling fluid pulse signal[J]. Oil Drilling & Production Technology, 2000, 22(4): 8-10.(in Chinese)

[15]Klotz C, Kaniappan A, Thorsen A K. A new mud pulse telemetry systems reduce risks when drilling complex extended reach well[C]∥IADC/SPE Asia Pacific Drilling Technology Conference and Exhibition. Jakarta, Indonesia: Society of Petroleum Engineers, 2008:1-12.

[16]何树山, 刘修善. 钻井液正脉冲信号的衰减分析[J].钻采工艺, 2001, 24(6):1-12.

He Shushan, Liu Xiushan. Analysis of signal attenuation for positive drilling fluid pulse[J]. Drilling & Production Technology, 2001, 24(6): 1-12. (in Chinese)

[17]Klotz C, Bond P, Wasserman I, et al. A new mud pulse telemetry system for enhanced MWD/LWD application[C]∥IADC/SPE Drilling Conference. Orlando, Florida: Society of Petroleum Engineers, 2008:1-5.

[18]王翔, 王瑞和, 纪国栋. 井筒内钻井液连续脉冲信号传输频率相关摩阻模型[J]. 石油学报, 2009, 30(3): 445-449.

Wang Xiang, Wang Ruihe, Ji Guodong. Frequency dependent friction model for consecutive pulse signal of drilling fluid transmitting in borehole[J]. Acta Petrolei Sinica, 2009, 30(3): 445-449.(in Chinese)

[19]罗志昌. 流体网络理论[M]. 北京：机械工业出版社, 1988: 14-23.

10.16450/j.cnki.issn.1004-6801.2016.04.011

国家自然科学基金资助项目(61004067)

2014-07-30；

2014-10-10

TE937；TH812

刘均，男，1976年8月生，副教授。主要研究方向为井下仪器与装置的研发。曾发表《钻柱内连续波信号传输模型与幅频特性研究》(《仪器仪表学报》2015年第1期)等论文。

E-mail: dragon2k@163.com