The numerical and experimental investigations of the near wake behind a modified square stay-cable*
Shun-cheng SHEN (沈顺成), Miao WANG (汪秒), Hong LU (卢红), Lin ZOU (邹琳)
School of Mechanical and Electronic Engineering, Wuhan University of Technology, Wuhan 430070, China,
E-mail: whut517@126.com
The numerical and experimental investigations of the near wake behind a modified square stay-cable*
Shun-cheng SHEN (沈顺成), Miao WANG (汪秒), Hong LU (卢红), Lin ZOU (邹琳)
School of Mechanical and Electronic Engineering, Wuhan University of Technology, Wuhan 430070, China,
The near wake structure, the wake-flow characteristics and the drag coefficients behind a modified square stay-cable(MSC) with sinusoidal variations of the cross-section area along the spanwise direction are investigated experimentally and numerically. The Reynolds numbers are chosen as 100 and 500 for the laminar flow and =Re6 000 and 22 000 for the turbulent flow. The detailed near wake structures, the velocity fields and the force coefficients for the MSC are captured, the effect of the Reynolds number on the flow structure for the MSC is studied. The numerical and experimental investigations show that the free shear layers from the leading edge are widened and prolonged and then roll up into vortices further downstream the MSC, unlike a straight square stay-cable (SSC) under the same flow conditions. As a result, the distinct mean drag reduction and the fluctuating lift suppression are observed for all Reynolds numbers, a drag reduction of at least 15.8% and the rms lift coefficient reduction of up to 95% are observed, as compared with the case of a straight square stay-cable at =500Re.
modified square stay-cable (MSC), wake structure, flow control, drag reduction
Introduction
The flow around bluff bodies, such as cylinders,chimneys and square stay-cables, is an important technical problem associated with the energy conversion and the structural design. The fluid-dynamic vibration of a rectangular slab was the subject of extensive numerical and experimental investigations and many interesting physical phenomena were observed[1-5]. Meliga et al.[6]discussed the sensitivity of aerodynamic forces on a square cylinder. Leontini et al.[7]studied the fluid-structure interaction of a square cylinder at different angles of attack. Fu et al.[8]observed the strong 3-D characteristics of the flow past a square cylinder at Re=300 by using CFX software. Samani and Bergstrom[9]investigated the effect of a wall on the wake dynamics of an infinite square cylinder. De Stefano and Vasilyev[10]carried out the numerical simulations of 3-D flow past a square cylinder by employing the wavelet-based adaptive method.
Many methods were proposed over the recent years to control the wake vortex dynamics with the aim of weakening the vortex shedding and reducing the amplitude of the fluctuating lift as well as the drag. Both passive and active controls were investigated in the past[11]. Active methods involving the energy input to a flow structure system to bring about desirable changes of the system. Passive schemes require no external energy input, typically changing the geometry of the structures or adding fixed mechanical vortex disturbers to influence the vortex shedding. Bearman and Owen[12]observed that the rectangular cross-section bodies with a mild wavy (wave steepness of only 0.06 to 0.09 trailing edge resulted in the complete suppression of vortexshedding and a substantial drag reduction of at least 30% at Re=40000. Darekar and Sherwin[13]suggested that the primary wavelength of the straight square-section cylinder might lead to the suppression of the Karman street. Lam and Lin[14]showed that both the mean drag coefficients and thefluctuating lift coefficients of a wavy circular cylinder were evidently smaller than those of a purely circular cylinder. Malekzadeh and Sohankar[15]studied the reduction of fluid forces and heat transfer on a square cylinder using a control plate. Abograis and Alshayji[16]studied an additional passive control method to reduce the fluid forces on a square cylinder in a laminar flow. Huang et al.[17]employed the modulation of a planar jet issued from upstream surface to reduce the forces on a square cylinder. Carassale et al.[18]investigated experimentally the effect of the rounded corners on the aerodynamic behavior of square cylinders. Rashidi et al.[19]studied the control of the wake structure behind a square cylinder by magnetohydrodynamics.
The purpose of our work is to carry out the PIV experiment measurements and numerical studies of the three-dimensional flow around a modified square stay-cable (MSC) with sinusoidal variations of the cross-section area along the spanwise direction over a wide Reynolds number range (from 100 to 22 000) to investigate their advantages in the flow control and the drag reduction. The main objectives are as follows:(1) to determine the wake structures around and behind the MSC, (2) to calculate and analyze the difference of the drag coefficient, the root-mean-square (rms) lift coefficient and the pressure characteristics between the straight square stay-cable (SSC) and the MSC, (3) to verify the mechanism of the flow control and the drag reduction by using the modified surface of the square stay-cable. Such experimental and computational results are to establish a comprehensive database to further our understanding of the physical mechanisms of the 3-D flow characteristics for the MSC and of the physical mechanisms of the control of the flow induced vibration and drag reduction.
1 PIV setup and flow measurement
The particle image velocimetry (PIV) measurements are conducted using a Dantec standard PIV2100 system. Fig.1 shows the schematic diagram of the experimental setup. The present measurements are carried out in a low-speed closed-loop water tunnel with a square working section of 0.3 m×0.6 m and a length of 2.4 m. The MSC of width Dm=0.015m and height Dz=Dm+2acos(2πz/λ) with a length of 0.3 m is placed horizontally. Here,zD denotes the local height of the MSC and varies in the spanwise direction z. The sinusoidal wavelength λ, the wave amplitude a and the mean diametermD of the MSC are fixed at λ/Dm=5.6 and a/Dm=0.175, respectively (Fig.1) The axial location of the maximumzD is called the“node”, while the location of the minimumzD is called the “saddle”. A SSC of diameter Dm=0.015m is also introduced for comparison. The present measurements are conducted at =U∞0.033 m/s and 0.335 m/s, corresponding to =Re500 and 6 000, respectively.

Fig.1 Experimental setup
2. Computational methods
In the present simulations, the Reynolds numbers are kept at =Re100 and 500 for the laminar flow and Re=6 000 and 22 000 for the turbulent flow. At the low Reynolds numbers, the unsteady 3-D laminar flow of a viscous incompressible fluid is considered. The dimensionless 3-D Navier-Stokes equations governing the flow of a Newtonian fluid can be written in the vector form as:

where the non-dimensional velocity vector u in theCartesian coordinates (,,)xyz has three velocity components u, v, and w, respectively, p is the nondimensional static pressure. The Reynolds number is defined as: Re=U∞Dm/ν, where ν is the fluid kinematic viscosity. In solving the governing equations, the different physical quantities are normalized by the free-stream velocity and the mean diametermD. The finite volume method (FVM) with an unstructured hexahedral grid is employed to solve the unsteady incompressible 3-D Navier-Stokes equations. The pressure velocity coupling is handled with the semi-implicit pressure linked equations (SIMPLE) scheme. Discretization of the convective terms in the conservation equations is realized through a second-order accurate upwind differencing scheme. The second-order implicit forward discretization is adopted for the time derivative term in order to accelerate the convergence process.
In the high Reynolds number regime, the 3-D large eddy simulation (LES) turbulence model is implemented also based on the FVM. The large scale eddies are solved directly by the filtered Navier-Stokes equations, and the small eddies are modeled using a subgrid scale (SGS) model. The detailed descriptions and validation tests of the present LES for the turbulence flow past bluff bodies can be found in Ref.[20].
In the present simulations, the computational boundaries are set at 16mD in y direction. The upstream boundary is set at 8mD away from the leading edge of the MSC. The downstream boundary is 16mD away from the trailing edge of the MSC. The spanwise length of the MSC is set equal to the wavelength λ. At the inlet boundary, uniform oncoming flows with components U∞are imposed. The Neumann-type boundary condition is used at the outlet boundary. The spanwise direction of the computational domain is assumed to satisfy the periodic boundary condition and a no-slip boundary condition (u=v=w=0) is prescribed at the surface of the MSC. The lateral surfaces are treated as slip surfaces using symmetry conditions.
The computational domain and the grid distributions are shown on Fig.2. In the laminar flow cases,the distance of the first grid near the square surface is 0.01mD. The number of meshes around the stay-cable circumference is 120 and the number of mesh layers along the stay cable spanwise direction is 56. In the turbulent flow cases, the distance from the stay cable surface to the nearest grid points is fixed as+y. The number of meshes around the cylinder circumference is 170 and the number of mesh layers along the cylinder spanwise direction is 72.
3. Results and discussions
Darekar and Sherwin[13]pointed out that the optimal wavelength was around 5.6mD for the drag reduction of a wavy square cylinder at low Reynolds numbers. Therefore, we might expect a drag reduction by employing a MSC with an optimal wavelength for the best effect on the FIV suppression. As a result, a MSC with a spanwise wavelength ratio of λ/Dm=5.6 and a fixed wave amplitude of a/Dm=0.175 is employed in all present experiment measurements and numerical simulations. Furthermore, the influence of the Reynolds numbers (=Re100 to 22 000) on the MSC is considered.
3.1Weak structures
Figure 3 and Fig.4 show the normalized instantaneous spanwise vorticity and the normalized mean streamwise velocity behind the MSC by using the PIV measurement at =Re500 and 6 000, respectively. Compared with the case of the SSC, the 3-D free shear layers are pushed further downstream behind the MSC both at =Re500 and 6 000. And the wavy surfaces of the MSC lead to a varied wake width at different spanwise positions, the wakes are wide behind the nodal position and narrow behind the saddle position and they roll up into vortices further downstream the MSC (see Fig.3). Similar trend can be found in Fig.4. The values of the vortex formation length of the MSC are evidently larger at =Re500 and 6 000, and along the spanwise direction of the MSC, they show a distinctvariation (see Fig.4). These will lead to the development of well organized 3-D free shear layers with a periodic repetition along the spanwise direction for the MSC. It also implies that the mean drag coefficients of the MSC will be smaller than those of the SSC.
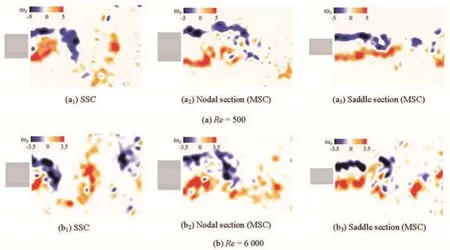
Fig.3 (Color online) Normalized instantaneous spanwise vorticity behind the MSC by PIV
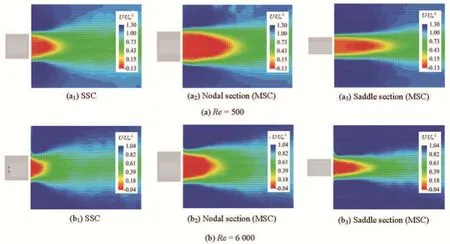
Fig.4 (Color online) Normalized mean streamwise velocity behind the MSC by PIV
Figure 5 shows the instantaneous wake structures of the SSC or the MSC in the -xy plane at =Re100,500, 6 000 and 22 000, obtained by the numerical simulations. These computational results are in excellent agreement with the present experimental PIV measurements (refer to Fig.3) and previous published numerical results obtained by Sohankar et al.[1]and Saha et al.[2]. They indicate that the present numerical schemes are applicable for both the low and high Reynolds number regimes. As shown in Fig.5, the wake structure characteristics are clearly illustrated by the vorticity distribution around and behind the SSC and MSC. Around both the SSC and the MSC, the flow separation occurs at the leading edge at all cases of the Reynolds numbers, with a periodic shedding of vortices, dominating the near wake of the stay-cable. However, for the MSC, at all cases of the Reynolds numbers, because of the variations of the modified leadingedge along the spanwise direction, the free shear layers in the streamwise direction extend behind both the nodal section and the saddle section, while in the transverse direction, they extend only behind the nodal section of the MSC. This is the cause of the free shearlayer instability from the MSC at a further downstream position, and the 3-D free shear layers with a periodic repetition along the spanwise direction are well organized and become more stable at the near wake behind the MSC. On the other hand, with the increase of the Reynolds number, the free shear layers roll up into vortices more rapidly and increase the turbulent nature of the vortices for both the SSC and the MSC. However,with the same Reynolds number, vortices roll up at a further downstream position for the MSC as comparedwith the SSC. It suggests that the mean drag and the lift fluctuation coefficients of the MSC will be greatly reduced over such wide range of Reynolds numbers than those of the SSC.
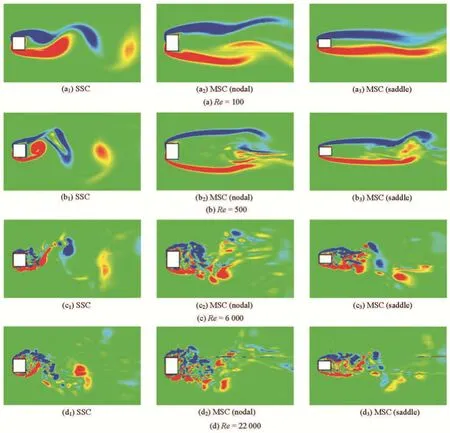
Fig.5 (Color online) Instantaneous wake structures of the SSC or the MSC in the -xy plane
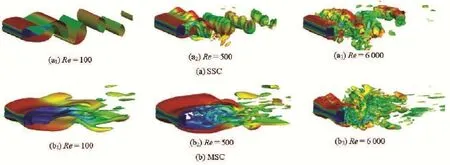
Fig.6 (Color online) Instantaneous 3-D wake structures of the SSC and the MSC

Fig.7 Time history of force coefficients of the SSC and the MSC
Figure 6 shows the instantaneous 3-D wake structures of the SSC and the MSC at =Re100, 500, and 6 000. For the MSC, the 3-D wake features are enhanced distinctly due to the effect of the wavy surface. The significant spanwise flow moves from the saddle section toward the nodal section. It means that the near wake structures are modified by this kind of wavy surface. The 3-D free shear layers are larger and more stable than those from the SSC. The formation of dislocations in the wake of the MSC reduces the mean drag coefficient and the rms lift coefficient.
3.2Force characteristics
Figure 7 shows the time history of the force coefficients for both the SSC and the MSC. From the drag force component of the MSC, a significant drag reduction and lift fluctuation suppression can be seen as compared with the SSC at all Reynolds numbers. For the SSC at Re=500, the mean drag coefficient=2/ρDH), the rms fluctuating lift coefficient'=2'/ρDH), and the Strouhal number(St=fsD/U∞) obtained by the present numerical results are 1.956, 1.05, and 0.141, respectively. Here, FDis the total mean drag force, F' is the rms. lift force andsf is the vortex shedding frequency obtained by the fast fourier transform (FFT) of the time history of the fluctuating lift. For the MSC, the values ofDC,LC' and St are 1.646, 0.012 and 0.095,respectively. That is to say, the drag reduction of at least 15.8% and the rms lift coefficient reduction of up to 95% with a lower shedding frequency are observed as compared with the SSC at Re=500. With the increase of the Reynolds number, the advantageous features of the MSC gradually are alleviated but still exist. These results show that the MSC with such a wavy surface is good for the control of the FIV.
3.3Pressure distributions
Figure 8 shows the variation curves of the mean pressure coefficient on the peripheral of the SSC and the MSC, that is, on Faces 01, 12, 23 and 30. Our LES calculations are similar to those obtained in previous researches. For all Reynolds numbers, and for both the SSC and the MSC, the profiles ofpC on Face 01 are symmetric with respect to the stagnation point, where the maximumpC of 1.1 occurs. The minimumpC(the separation point) occurs at the vertices 0 and 1. ThepC curves on Faces 12 and 30 are similar because of the symmetry. But for the profiles ofpC on Faces 12, 23 and 30, the values for the MSC are larger than those for the SSC, especially at =Re500 and6 000. From the above discussions, we conclude that a MSC with a smaller pressure difference can lead to a significant drag reduction.
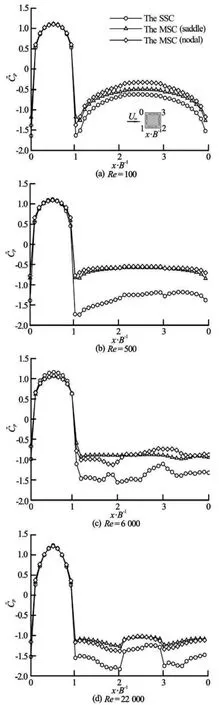
Fig.8 Variation curves of mean pressure coefficient on the peripheral of the SSC and the MSC
4. Conclusions
This paper presents a study of 3-D flow past a MSC for =Re100, 500, 6 000 and 22 000 by using PIV measurements and 3-D numerical simulations. The following observations are made:
The present numerical results for the SSC show a good agreement with the present PIV experimental results and the previous published numerical results. It means that the present simulation model is validated.
For the MSC, the mean drag coefficient reduction and the fluctuating lift suppression are observed for all Reynolds numbers of 100, 500, 6 000 and 22 000 as compared with that of the SSC. It is mainly due to the existence of well organized transverse vortices along the spanwise direction, which stabilize and elongate the free shear layers from the leading edge and these free shear layers roll up into vortices at a further downstream position. A drag reduction of at least 15.8% and the rms lift coefficient reduction of up to 95% are observed as compared with the SSC at =Re 500.
As the Reynolds number increases, the advantageous of the flow control and the drag reduction for the MSC are gradually alleviated but still exist.
It implies that the optimum wavy surface is a good choice for the drag reduction and the fluctuating suppression for the MSC under both the laminar and turbulent flow conditions.
References
[1]SOHANKAR A., NORBERG C. and DAVIDSON L. Numerical simulation of unsteady low-Reynolds number flow around rectangular cylinders at incidence[J]. Journal of Wind Engineering and Industrial Aerodynamics,1997, 69-71: 189-201.
[2]SAHA A. K., BISWAS G. and MURALIDHAR K. Threedimensional study of flow past a square cylinder at low Reynolds numbers[J]. International Journal Heat and Fluid Flow, 2003, 24(1):54-66.
[3]SEN S., MITTAL S. and BISWAS G. Flow past a square cylinder at low Reynolds numbers[J]. International Journal for Numerical Methods in Fluids, 2011, 67(10): 1160-1174.
[4]ZHANG Wei, DAI Yu-man. Numerical study of flow around three equispaced square cylinders at low reynolds number[J]. Journal of Mechanical Engineering, 2015,51(12): 185-191(in Chinese).
[5]YOUNIS B. A., ABRISHAMCHI A. Three-dimensional turbulent vortex shedding from a surface-mounted square cylinder: Predictions with large-eddy simulations and URANS[J]. Journal of Fluids Engineering, 2014, 136(6): 060907.
[6]MELIGA P., BOUJO E. and PUJALS G. et al. Sensitivity of aerodynamic forces in laminar and turbulent flow past a square cylinder[J]. Physics of Fluids, 2014, 26(10): 104101.
[7]LEONTINI J. S., JACONO D. L. and SHERIDAN J.Fluid-structure interaction of a square cylinder at different angles of attack[J]. Journal of Fluid Mechanics, 2014,747: 688-721
[8]FU Ying-nan, ZHAO Xi-zeng and WANG Xing-gang. Three dimensional numerical simulation of flow past a square cylinder using CFX[J]. Chinese Journal of Hydrodynamics, 2015, 30(4): 382-389(in Chinese).
[9]SAMANI M., BERGSTROM D. J. Effect of a wall on the wake dynamics of an infinite square cylinder[J]. International Journal of Heat and Fluid Flow, 2015, 55(10): 158-166.
[10] De STEFANO G., VASILYEV O. V. Wavelet-based adaptive simulations of three-dimensional flow past a square cylinder[J]. Journal of Fluid Mechanics, 2014, 748: 433-456.
[11] LUO Yuehao, WANG Liguo and GREEN Lork et al. Advances of drag-reducing surface technologies in turbulence based on boundary layer control[J]. Journal of Hydrodynamics, 2015, 27(4): 473-487.
[12] BEARMAN P. W., OWEN J. C. Reduction of bluff-body drag and suppression of vortex shedding by the introduction of wavy separation lines[J]. Journal of Fluids and Structures, 1998, 12(1): 123-130.
[13] DAREKAR R. M., SHERWIN S. J. Flow past a bluff body with a wavy stagnation face[J]. Journal of Fluids and Structures, 2001, 15(3-4): 587-596.
[14] LAM K., LIN Y. F. Effects of wavelength and amplitude of a wavy cylinder in cross-flow at low Reynolds numbers[J]. Journal of Fluid Mechanics, 2009, 620: 195-220.
[15] MALEKZADEH S., SOHANKAR A. Reduction of fluid forces and heat transfer on a square cylinder in a laminar flow regime using a control plate[J]. International Journal of Heat and Fluid Flow, 2012, 34(4): 15-27.
[16] ABOGRAIS A. S., ALSHAYJI A. E. Reduction of fluid forces on a square cylinder in a laminar flow using passive control methods[C]. The Proceedings of the 2013 COMSOL Conference. Boston, USA, 2013, 157-163.
[17] HUANG R. F., HSU C. M. and CHIU P. C. Flow behavior around a square cylinder subject to modulation of a planar jet issued from upstream surface[J]. Journal of Fluids and Structures, 2014, 51(11): 362-383.
[18] CARASSALE L., FREDA A. and MARRÈ-BRUNENGHI M. Experimental investigation on the aerodynamic behavior of square cylinders with rounded corners[J]. Journal of Fluids and Structures, 2014, 44(1): 195-204.
[19] RASHIDI S., BOVAND M. and ESFAHANI J. A. et al. Control of wake structure behind a square cylinder by Magnetohydrodynamics[J]. Journal of Fluids Engineering, 2015, 17(1): 35-67.
[20] ZOU Lin, LIN Yu-feng. Force reduction of flow around a sinusoidal wavy cylinder[J]. Journal of Hydrodynamics,2009, 21(3): 326-335.
E-mail: whut517@126.com
(December 12, 2015, Revised January 5, 2016)
* Project supported by the National Natural Science Foundation of China (Grant Nos. 11172220, 51275372).
Biography: Shun-cheng SHEN (1959-), Male, Master,Associate Professor
Lin ZOU, E-mail: l.zou@163.com
- 水动力学研究与进展 B辑的其它文章
- The 2nd Conference of Global Chinese Scholars on Hydrodynamics 2016.11.11~14, Wuxi
- The mechanism of flapping propulsion of an underwater glider*
- A new design of ski-jump-step spillway*
- A water quality model applied for the rivers into the Qinhuangdao coastal water in the Bohai Sea, China*
- The hydraulic characteristics of end-dump closure with the assistance of backwater-sill in diversion channel*
- Natural convective heat transfer and nanofluid flow in a cavity with top wavy wall and corner heater*

