考虑路网随机性的地铁和道路公交网络优化*

陈玲娟 伍景琼 鲁寒宇

(1.武汉科技大学汽车与交通工程学院,430081,武汉; 2.昆明理工大学交通工程学院,650500,昆明∥第一作者,讲师)



考虑路网随机性的地铁和道路公交网络优化*

陈玲娟1伍景琼2鲁寒宇1

(1.武汉科技大学汽车与交通工程学院,430081,武汉; 2.昆明理工大学交通工程学院,650500,昆明∥第一作者,讲师)

为发挥轨道交通的骨干运输功能,优化综合公共交通出行网络,建立了基于既有轨道交通路网的地面道路公交调整双层规划模型。上层规划考虑综合公交网络客运量及轨道交通客运周转量最大化、总社会出行成本及车辆配备成本最小化共4个目标,下层模型以效用理论为基础构建弹性需求下的线路流量分配,其中地面道路公交线路的出行效用考虑了道路通行能力的随机性。采用蒙特卡罗模拟求解下层模型,并采用基于向量的多目标粒子群算法求解整体双层规划,获得最佳调整线路的走向和发车间隔。最后通过算例验证了模型和算法。计算结果表明:所得到的解为一组Pareto解,4个目标间存在相悖关系。在实际问题中,应结合改造成本和现实需要来选取最优解作为调整方案。

公交调整; 双层规划; 蒙特卡罗模拟; 多目标粒子群算法

First-author′s address School of Automobile and Traffic Engineering,Wuhan University of Science and Technology,430081,Wuhan,China

随着城市化进程的加快,公共交通特别是轨道交通在很多城市得到了快速发展。轨道交通的快速和大运量缓解了出行压力,且对城市土地开发起到了一定的导向作用,改变了既有的出行OD(起点-终点)分布。因此,轨道交通走向和站点设计等规划要素应以缓解既有出行拥挤为基础,同时兼顾其带动区域经济发展产生的诱增出行需求转移。

目前,常规地面公交通常是伴随轨道交通网络开通进行局部调整,以配合轨道交通疏散聚集点的需求,从而达到优化整体公交网络的目的。本文探讨城市轨道交通投入运营后,配套的地面道路公交调整措施。

既有地面道路公交研究目前多集中在地面道路公交网络设计问题(TNDP),国内外学者从模型构造和算法设计两方面探讨了TNDP。模型构造方面主要考虑了与其他运输方式的竞争及公共交通自身线路、服务频次等要素的设计[1-3],模型求解方面多采用启发式算法求解实际网络[4-6]。然而,考虑城市轨道交通运营下的地面道路公交调整有其独特性。首先,二者运营特征不同,在整体道路公交网络中存在竞争关系;其次,与TNDP优化目标不同,地面道路公交调整需保障城市轨道交通的骨干运输功能,同时接续轨道交通,完善整体出行路网;再次,地面道路公交调整多为局部调整,在既有路网基础上调整与轨道交通走向相关的线路,与TNDP中的重新布设存在区别。

在地面道路公交调整方面,文献[7]提出了基于轨道交通与地面道路公交一体化的公交线路及站点调整方法,文献[8]探讨了基于轨道交通的接运公交网络优化,文献[9]从道路公交线路走向和运营参数角度研究了优化调整方法。这些文献均从定量的角度探讨了地面道路公交调整,然而缺乏对出行行为的细致分析。

实际的地铁和道路公交路网不仅面临外部运输方式的竞争,其内部也存在效用差别。在既有的城市轨道交通网络条件下,地面道路公交的走向、停靠站点、发车频次、配备车辆数等参数均会影响其竞争力,需从整体出行需求及出行行为角度进行定量分析。另外,城市轨道交通与地面道路公交运营性质不同,前者运营时间相对固定,而后者受到地面路网随机性影响,运行时间与间隔时间等均不确定。

基于上述分析,本文以出行行为为基础,建立地面道路公交调整的双层规划模型。上层模型以城市轨道交通输送量最大、整体道路公交路网服务量最大等为优化目标,下层模型采用效用理论描述出行方式及线路选择行为,并在地面道路公交效用计算中考虑路网日常拥挤对道路公交运行时间和站点间隔的影响,分析整体道路公交网络与其它方式的竞争,依据效用最大化在备选路径间分配流量,并结合多目标粒子群算法求解模型。

1 综合公交网络出行行为分析

城市综合公交网络包括轨道交通、常规地面道路公交、水上公交及BRT(巴士快速交通)等多种形式。本文主要讨论城市轨道交通与常规道路公交间的协调。城市轨道交通线路走向确定后,会导致沿线土地利用、城市布局及人口分布的变化,从而带来不同的交通出行需求。既有地面道路公交线路不再适应变化中的出行需求,需要根据新的OD出行数据对线路进行调整。

1.1 公交网络输入条件及相关假设

为合理分析综合公交网络下的出行者出行方式及路线选择,并优化整体公交网络,对研究问题做出如下假设:

1) 综合公交网络优化是在城市轨道交通投入运营后,根据轨道交通与既有道路公交线路走向关系,在遵从出行行为条件下做出调整。两者之间关系包括交叉、重叠、接驳等,根据道路设施和相关站点位置给出在网络结构上三类线路的备选走向集合。本文仅研究出行选择和最优线路布设,道路公交线路备选集合的具体方法可参考文献[9]。

2) 城市轨道交通投入运营后,导致土地开发变化,改变了交通需求分布。假设新需求OD已通过土地价格预测和交通需求预测的四阶段法测得。

3) 公交换乘给乘客带来极大不便,包括等待时间延长、走行距离增加等。假设出行者选择换乘线路时,设定二次换乘为出行者可接受的最大换乘次数。

4) 道路公交网络优化调整过程中,已投入运营的城市轨道交通线路的运营参数作为输入条件保持恒定不变,包括线路走向、停靠站点、发车间隔时间及票价等。

5) 为简化研究主体复杂性,设定同一条公交线路上、下行线路走向与站点位置相同(不考虑个别特殊线路)。

1.2 基于线路效用的出行选择行为

公共交通网络中可选择的出行方式包括城市轨道交通、地面道路公交或两者换乘出行等多种方式,且每种出行方式又包含多条线路。根据出行效益最大化原则,乘客出行选择广义费用最小的线路,且由于与私家车、出租车等其他出行方式存在竞争,选择公共交通出行的乘客总量随总出行成本增加而减少,体现出弹性需求特性。因此,可采用随机效用理论描述弹性需求下出行方式及线路的选择行为。

考虑交通网络G(N,A),其中N为网络节点集合,A为路段集合。W表示OD对集合,Dw表示某OD对w间的出行需求。公交线路(包含地铁线路),由一系列相连路段组成,表示为l=(n1,n2,…,nm),其中ni为路径l第i条路段的起点,ni+1为路径l第i条路段的终点,不同公交线路包含不同路径节点。L表示从起点到终点的出行线路。

定义第j种出行方式的费用函数f和效用函数U分别表示为

(1)

式中:

f——出行线路的费用函数;

θ——参数;

xj——出行线路的第j个特性值,本文考虑出行方式特性依次为出行时间、等待时间和票价。

OD对w之间的乘客完成出行,可选择出行线路有以下几种:

1)L仅包含城市轨道交通一种出行方式,则

(2)

2)L仅包含地面道路公交一种出行方式,则

(3)

3)L包含城市轨道交通和地面道路公交两种出行方式,则

(4)

(5)

Fl(l∈Lrail)由线路长度Le,l及轨道交通里程运价计算;Fl(l∈Lbus)则根据车型定价。

2 网络优化的双层规划模型

2.1 上层模型优化目标

地铁公交网络调整优化目标是使得轨道交通承担干线功能,整体公交网络输送乘客量最大,且出行者根据效益最大化选择出行线路。本文建立双层规划模型描述公交线路调整,上层模型为公交网络布局规划的目标函数及约束条件,下层模型描述在地面公交走行时间随机分布条件下乘客对公共交通线路的选择模型。公交线路调整模型的目标函数如下:

1) 公交网络有效服务乘客总量最大化

(6)

式中:qw表示弹性需求下OD对w间选择公共交通出行的总流量。

2) 轨道交通输送客流周转量最大化。优化调整常规公交网络的主要目的之一,是减少地面公交线路与轨道交通线路的竞争,发挥轨道交通对客流的快速疏散作用。轨道交通客流周转量最大化表示为

(7)

3) 乘客平均公交出行成本最小化。考虑乘客的出行成本包括乘车时间、等车时间及支付的公交票价,享有公交有效服务的乘客总乘车时间表示为

(8)

式中:第1、2项分别表示在地面道路公交线路和轨道交通线路中的乘车时间。

给出的公共服务系统中等待时间计算公式如下

(9)

式中:第1、2项分别表示乘客在地面道路公交线路及轨道交通线路中的总等待时间。

乘客出行总票价计算公式如下:

(10)

因此,乘客平均出行成本最小化目标表示如下:

(11)

式中βi表示决策者对目标的权重。

4) 车辆配备成本最小化。为简化计算,地面公交配置成本中仅考虑车辆的配置费用为

(12)

在公交线路布局中,需综合考虑线路长度,发车间隔等因素,因此,结合4个目标函数及相应约束条件,构建多目标规划的上层模型如下

约束条件:

(1) 线路总长度约束,Le,min≤Le,l≤Le,max,其中Le,min、Le,max分别表示线路的最小及最大长度约束;

(2) 同一线路上车次间隔时间约束,tmin≤tl,r≤tmax,其中tmin、tmax分别表示同一线路上车次间隔时间的最小及最大值约束。

2.2 下层流量分配模型

考虑与小汽车出行的竞争,OD对w间公共交通出行需求qw表现为弹性函数,由公交出行服务质量决定,因此,下层模型为弹性需求下的随机流量分配。采用logit模型表述选择概率,得到乘客对出行线路L选择概率PL为

(13)

OD对w间总出行量qw弹性变化,表示为满意度Sw的函数,qw=Dw(Sw)。满意度函数Sw表示乘客选择最大效用方案的期望值

(14)

建立弹性需求下的随机平衡配流模型如下:

(15)

式中:qL表示选择线路L出行的流量。

3 模型求解

3.1 下层随机分配模型求解

下层模型中,由于公交线路走行时间及站点等待时间呈正态分布,故下层模型流量分配为一个随机问题,采用蒙特卡罗法模拟给定分布下线路走行时间及等待时间,并计算每次模拟数值下的选择流量,进而求解线路的平均出行流量。具体步骤为:

4) 终止条件:当迭代进行到指定次数s=M,则终止;否则令s=s+1,重复第③步。

5) 流量计算:根据蒙特卡罗模拟过程,计算

(16)

3.2 双层规划模型求解

1) 根据约束条件①检查备选集G中线路,满足长度约束则保留,否则删除。

2) 对保留的备选路网,采用VEPSO求解各线路最佳发车间隔,步骤如下:

(1) 初始化:设粒子群体个数为100,生成4个子群,每个子群包含25个粒子。子群k中第r个粒子的位置表示为xkr=(xkr1,xkr2,…,xkrm)(m为路网线路条数),速度为vkr=(vkr1,vkr2,…,vkrm);粒子初始位置为各条线路的最小发车间隔,初始速度为0.1,个体历最优点为pko,适应值为Zko;子群体历史最优点为pkg,适应值为Zkg;Vmax为tl,r变化范围tmin≤tl,r≤tmax。

(2) 适应值计算:将粒子位置作为tl,r带入下层模型。将子群1、2、3、4中粒子位置及下层模型求解数据分别代入式(6)、(7)、(11)、(12),计算粒子适应值zkr。

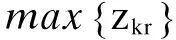
(4) 更新第K+1步的粒子速度和位置:

(5) 迭代终止条件:若未达到终止条件,转第(2)步。

4 实例分析

算例网络如图1所示。已知4个OD对:(3⇀13)、(1⇀14)、(3⇀7)、(2⇀9)。轨道交通线路走向为1⇀2⇀6⇀8⇀13。已有地面道路公交线路6条:3⇀2⇀4⇀12⇀11⇀10;1⇀2⇀4⇀6⇀15⇀7⇀10⇀14;3⇀6⇀8⇀15⇀7⇀10⇀13⇀14;7⇀15⇀8⇀6⇀3⇀2⇀5⇀4⇀12;5⇀4⇀6⇀8⇀10⇀7⇀15⇀9;1⇀2⇀3⇀6⇀8⇀10⇀11⇀13。轨道交通线路与地面道路公交关系包括:重叠路段1⇀2,调整策略选为缩短线路;重叠路段6⇀8,调整策略为改线,根据站间距约束备选线路为4⇀12⇀8或4⇀3⇀8;交叉道路公交路段11⇀10,调整策略为改线,备选线路11⇀13⇀10。图1中,路段22(18⇀8)为新增路段,用虚线表示,a(x)y表示路段x的长度为y。

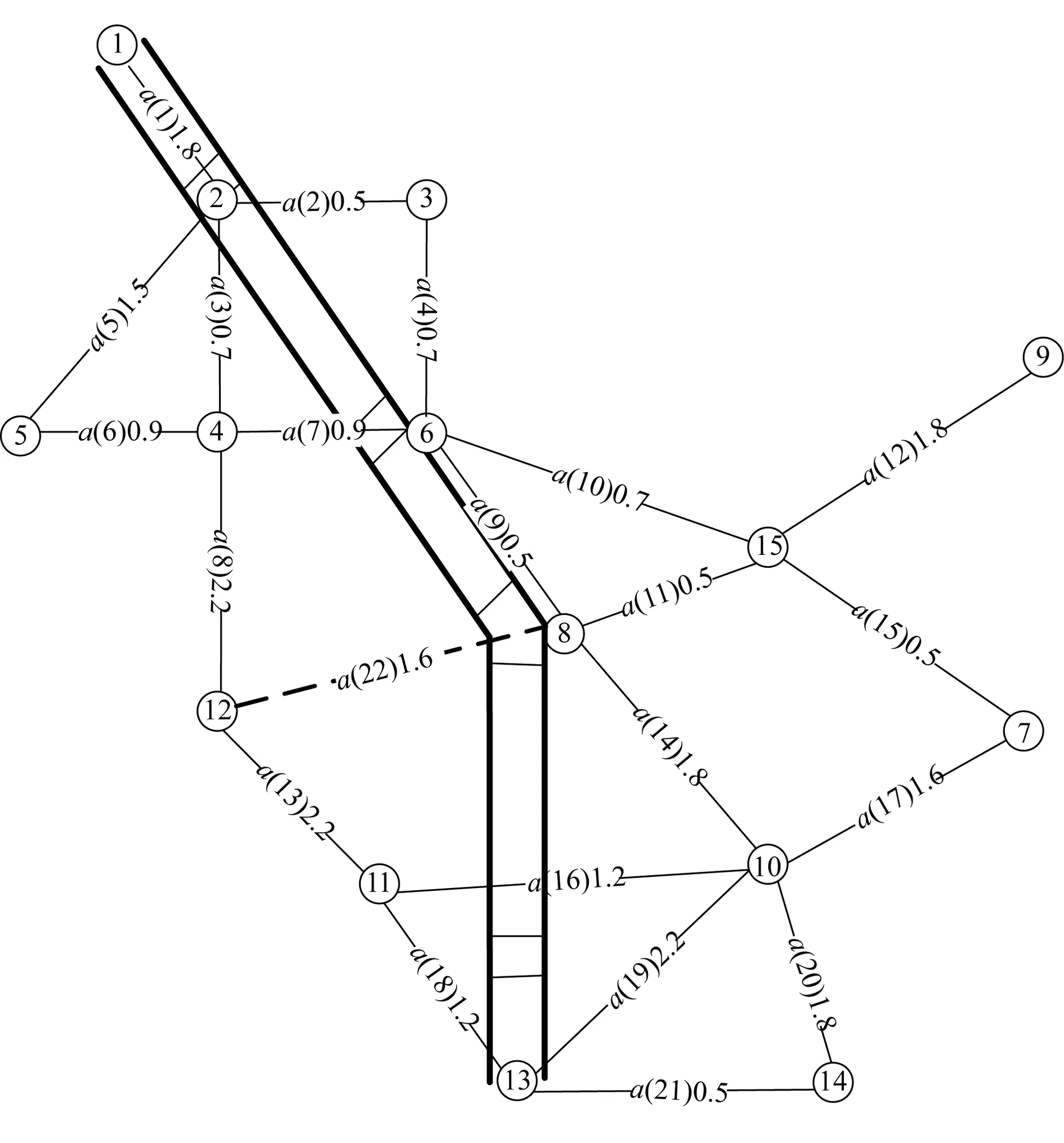
图1 算例网络

求解模型共得到一组Pareto解集。其中上层目标值,各车次发车间隔及调整后的线路走向如表1所示(其中第4列黑色字体表示线路有调整,否则表示线路维持原走向)。

表1 计算结果

从表1可看到,每个调整后的道路公交路网分别对应一组最佳发车间隔时间,且整体路网的4个目标存在相悖关系,因此实际决策中,还需结合实际需要选择最佳调整方案。

5 结语

地铁道路公交网络优化是在城市轨道交通网络建成后,为保障轨道交通的干线功能,优化整体公共交通路网而对既有地面道路公交线路做出调整。调整过程不仅要考虑线路的走向位置及网络拓扑结构,而且要考虑出行者选择行为,从而达到最大化输送能力的目的。本文基于效用理论描述出行选择行为,考虑到地面道路公交受道路通行能力随机性影响,采用蒙特卡罗模拟实际走行时间和到站间隔时间,建立了弹性需求下的随机线路流量选择模型,并将其作为下层模型,上层模型为道路公交路网性能优化的多目标模型。采用VEPSO方法得到了一组Paretto解。求解结果给出了调整线路的具体走向及最佳发车间隔。文中所建模型及方法对综合公共交通路网优化给出了一定的理论指引。

然而,模型中采用VEPSO方法求解,且下层模型嵌套蒙特卡罗模拟,当网络较大时,如何调整算法参数及迭代方程,从而缩小计算复杂度将是进一步研究方向。

[1] GALLO M,MONTELLA B,D’ACIERNO L.The transit network design problem with elastic demand and internalisation of external costs:An application to rail frequency optimisation [J].Transportation Research Part C:Emerging Technologies,2011,19(6):1276.

[2] GUIHAIRE V,HAO J K.Transit network design and scheduling:A global review [J].Transportation Research Part A:Policy and Practice,2008,42(10):1251.

[3] KEPAPTSOGLOU K,KARLAFTIS M.Transit route network design problem:review [J].Journal of transportation engineering,2009,135(8):491.

[4] BIELLI M,CARAMIA M,CAROTENUTO P.Genetic algorithms in bus network optimization [J].Transportation Research Part C:Emerging Technologies,2002,10(1):19.

[5] CHAKROBORTY P,WIVEDI T.Optimal route network design for transit systems using genetic algorithms [J].Engineering Optimization,2002,34(1):83.

[6] YAN Y,LIU Z,MENG Q,et al.Robust optimization model of bus transit network design with stochastic travel time [J].Journal of Transportation Engineering,2013,139(6):625.

[7] 陈丽君,陈学武,陆卫,等.基于轨道交通与公交一体化的公交线路及站点调整方法:201010593890.3[P].2011-08-17.

[8] 李诗灵,陈宁,赵学彧.基于粒子群算法的城市轨道交通接运公交规划[J].武汉理工学报(交通科学与工程版),2010,34(4):780.

[9] 孙杨.城市轨道交通新线投入运营下常规公交线网优化调整方法研究[D].北京:北京交通大学,2012.

[10] PARSOPOULOS K E,VRABATIS M N.Particle swarm optimization method in multi-objective problems[C]∥ACM Special Interest Group on Applied Computing.Proceeding of the 2002 ACM Symposium on Applied Computing.USA:ACM,2002:603.

[11] COELLO C A C,PULIDO G T,LECHUGA M S.Handling multiple objectives with particle swarm optimization [J].IEEE Transactions on Evolutionary Computation,2004,8(3):256.

[12] PARSOPOULOS K E,VRAHATIS M N.Recent approaches to global optimization problems through particle swarm optimization [J].Natural Computing,2002,1(2-3):235.

Metro/Bus Network Optimization Considering Network Stochastic

CHEN Lingjuan, WU Jingqiong, LU Hanyu

In order to ensure the leading role of railway and optimize the overall public transportation network,a bi-level programming model for bus line adjustment is established based on the existing railway network.The upper planning is aimed to maximize the whole transit network throughput volume,railway turnover volume and minimize the cost of total social travel and equipped vehicles.The lower model is to develop the flow distribution under elastic demand based on utility theory,and in the bus lines′ travel utility the randomness of road capacity us specially considered.Monte Carlo simulation is used to solve the lower model,Vector evaluated particle swarm optimization (VEPSO) is used to solve the whole bi-level programming,to obtain the adjusted bus line route and departure intervals.At the end,an example is adopted to test the model and algorithm,the results show that the solution is a group of Pareto solutions,four objections are contradicted.The optimum scheme for network design should be chosen by combining with cost and actual situations.

bus line adjustment; bi-level programming; Monte Carlo simulation; muti-objection particle swarm optimization

*国家自然科学基金项目(51308425);教育部博士后基金项目(2014M561762);大学生创新创业训练计划项目(201510488037)

U 121; U 491.1

10.16037/j.1007-869x.2016.08.007

2016-01-22)