豫北小尾寒羊部分体尺生长规律模拟

马发顺，李进萍，杨 信

（1.安阳工学院生物与食品工程学院，河南安阳455000；2.安阳市人民公园，河南安阳455000）

豫北小尾寒羊部分体尺生长规律模拟

马发顺1，李进萍2，杨 信1

（1.安阳工学院生物与食品工程学院，河南安阳455000；2.安阳市人民公园，河南安阳455000）

为了掌握豫北小尾寒羊部分体尺的生长规律，以3～24月龄豫北小尾寒羊的体高、胸围、管围和十字部高等4种体尺为材料，运用Logistic和von Bertalanffy这2种典型的非线性数学模型分别对4种体尺的生长发育过程进行拟合与分析。结果表明：Logistic和von Bertalanffy模型均能很好地描述豫北小尾寒羊体尺的实际生长情况，拟合度均在0.96以上，但von Bertalanffy模型更符合实际生长情况，模拟效果更好。体高、胸围、管围和十字部高4种体尺的生长模型的R2值分别为0.973、0.973、0.965和0.977，相应的体尺极限参数A分别为95.932、115.826、13.060和91.896，调节参数B分别为0.168、0.190、0.205和0.149，瞬时相对生长率k分别为0.098、0.069、0.039和0.112，最大周增长量分别为4.157、3.557、0.225和4.554cm· w-1，最大日增长量分别为0.594、0.508、0.032和0.651cm·d-1。von Bertalanffy模型在模拟3～24月龄豫北小尾寒羊4种体尺生长规律方面为理想的数学模型，绝对生长和相对生长均符合生长发育的一般规律。此研究结果可用于指导生产实践，也可为后续研究提供参考。

小尾寒羊；体尺；生长规律；生长模型；拟合

D01∶10.19329/j.cnki.1673-2928.2016.06.027

生长曲线的拟合是研究动物生长发育规律的重要手段，体尺生长模型的构建能够定量地描述其体尺生长发育的过程，更加准确地描述其生长规律。

豫北小尾寒羊是我国优良的地方品种，属于毛肉兼用型，在豫北及周边地区均有广泛饲养。该品种具有早熟多胎、常年发情、体格高大、生长发育快、肉用性能较好、耐粗饲、宜舍饲和放牧等优良种质特性。目前国内关于小尾寒羊的研究主要集中在饲养、繁殖和疾病防治等方面，关于肉用、裘用和生长发育的研究也有报道。胡永献等研究了其繁殖、裘用和肉用性能[1-3]，白哈斯[4]、郭继君[5]、胡永献等[6]分别对体重、体尺的生长情况进行了描述，田亚磊等[7]对体尺与体重的相关性进行了分析，马发顺等[8]对豫北小尾寒羊体重体尺间动态相关性进行了研究；姜勋平等[9]对萨槐杂种山羊建立了生长模型，梁学武等[10]和冯敏山等[11]分别对波尔山羊建立了生长模型，马发顺等[12]通过对豫北小尾寒羊生长模型的拟合，找到了最佳生长模型。而关于动物体尺生长发育规律的研究较少，特别是关于豫北小尾寒羊体尺的生长规律模拟的研究还未见报道，对小尾寒羊体尺指标进行生长模型建立还是空白。笔者通过对体高、胸围、管围和十字部高4种体尺的数学模拟，以揭示其生长发育的规律，为生产实践和相关理论研究提供参考。

1 材料与方法

1.1 材料

在河南省台前县小尾寒羊核心保护区选择3月龄断奶公羊30只，统一编号，混群饲养，体尺测量每间隔1个月测定1次，12月龄后18、24月龄各测定1次。使用测杖和卷尺等测量工具，测量项目有体高（Y1）、胸围（Y2）、管围（Y3）和十字部高（Y4）等。对原始数据求平均值[6]，测量结果见表1。

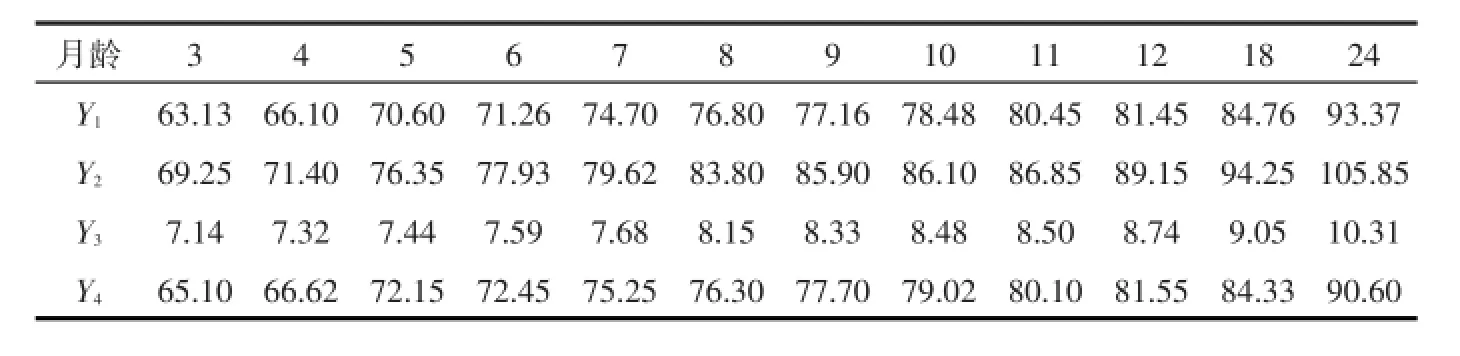
表1 小尾寒羊各月龄体尺 cm

1.2方法

1.2.1 生长模型及模型参数

两种模型函数表达式为：

Logistic模型 YL=A/[1+B·EXP(-k·t)]

von Bertalanffy模型 YB=A·[1－B·EXP(-k·t)]3

公式中，A为体尺极限参数，B为调节参数，k为瞬时相对生长率，t为月龄。方程参数估计采用麦夸特法，以残差平方和最小为目标函数，逐次迭代计算各参数值，以复相关系数（R2）作为衡量拟合优度指标。

1.2.2 生长参数计算方法

Logistic模型的生长参数：拐点体尺A/2，拐点日龄lnB/k，最大周增长量Ak/4，最大日增长量Ak/ 28。von Bertalanffy模型的生长参数：拐点体尺8A/ 27，拐点日龄ln(3B)/k，最大周增长量4Ak/9，最大日增长量4Ak/63。

1.2.3 生长发育指标计算方法

绝对生长计算方法：G=(r1－r0)/(t1－t0)；相对生长计算方法：R=(r1－r0)/[(r1＋r0)/2]×100%。公式中，r1为报告期体尺，r0为基期体尺；t1为报告期月龄，t0为基期月龄。

1.2.4 使用的统计软件

使用Excel2003软件进行数据处理，并使用该软件绘制曲线图。使用DPS v7.05软件（数学模型-单因变量-麦夸特法）进行回归分析。依次设定体高A（93）、B（0.86）、k（0.45）为初始值，胸围A （105）、B（0.75）、k（0.2）为初始值，管围A（10）、B （1）、k（0.41）为初始值，十字部高A（90）、B（0.5）、k （0.1）为初始值，进行Logistic曲线拟合。依次设定体高A（93）、B（0.19）、k（0.33）为初始值，胸围A （105）、B（0.17）、k（0.14）为初始值，管围A（10）、B （0.21）、k（0.29）为初始值，十字部高A（90）、B （0.13）、k（0.11）为初始值，进行von Bertalanffy曲线拟合。均收敛得到最佳结果。

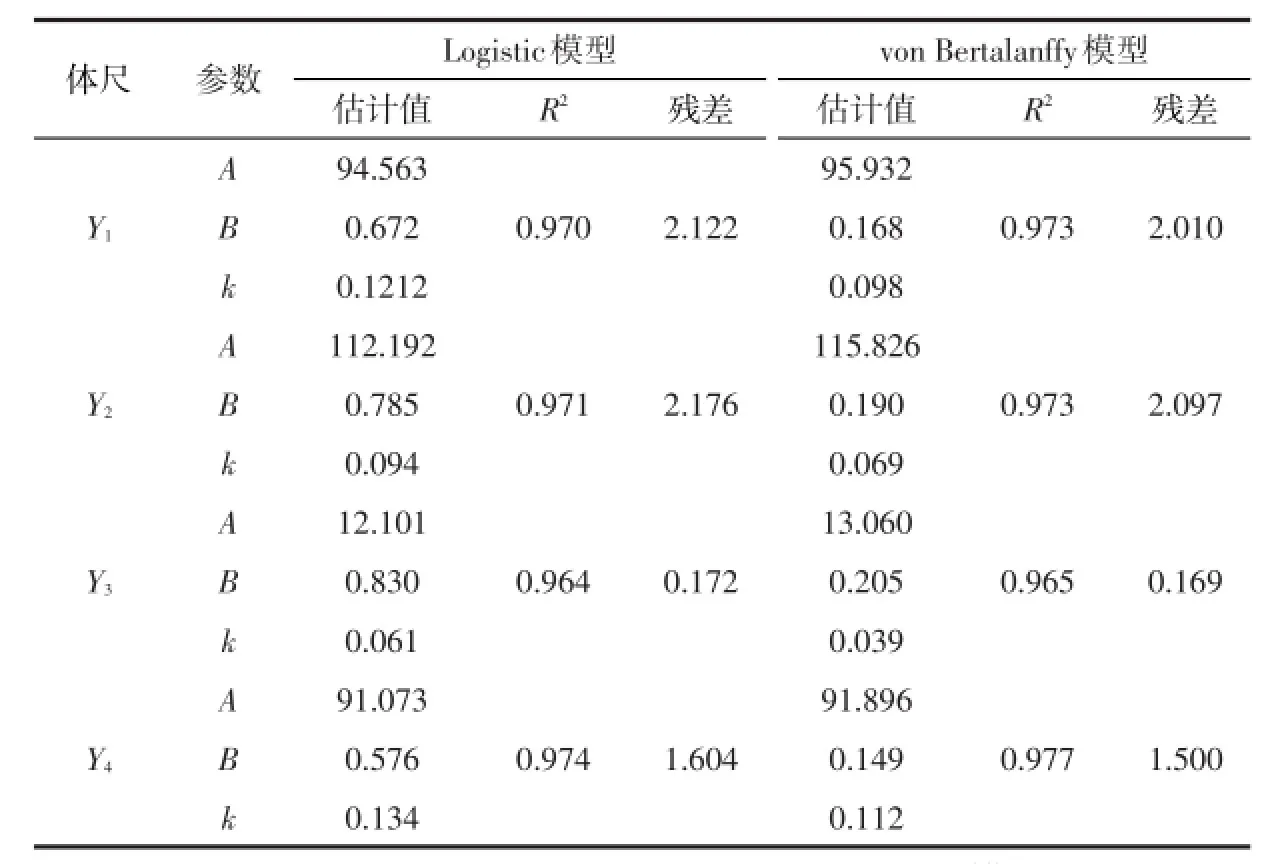
表2 生长模型参数估计值及拟合度

2 结果与分析

2.1 生长模型拟合结果

Logistic模型和von Bertalanffy模型中的参数估计值及拟合度指标见表2。对拟合得到的8个回归方程分别进行F检验，结果均达到了极显著水平（P＜0.01），对函数中的各个参数分别进行t检验，也均达到了极显著水平（P＜0.01）。说明8个回归方程参数估计的准确度很高，方程均真实有效。

根据两种模型分别计算出各月龄的理论体尺，然后用理论体尺与实际测量值进行比较，见图1、图2、图3、图4。从表2中两种模型的拟合度（R2）和残差比较可以看出，体高、胸围、管围和十字部高的von Bertalanffy模型的R2值（0.973、0.973、0.965、0.977）均高于Logistic模型，而von Bertalanffy模型的残差值（2.010、2.097、0.169、1.500）均分别小于Logistic模型。从图1、图2、图3和图4的拟合效果来看，von Bertalanffy模型估值更接近于实际测量值。可见，von Bertalanffy模型对体高、胸围、管围和十字部高的模拟均为最佳模型。

2.2 生长参数计算结果

依据von Bertalanffy模型获得的各体尺生长参数见表3，但是无法计算出有效的拐点月龄。

表3 豫北小尾寒羊体尺生长参数

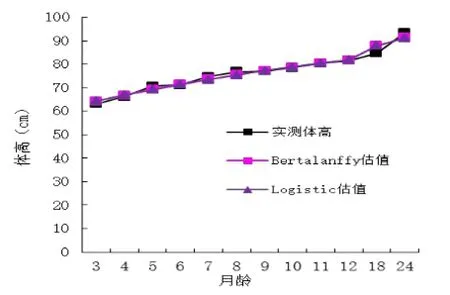
图1 两种生长模式对提高的拟合

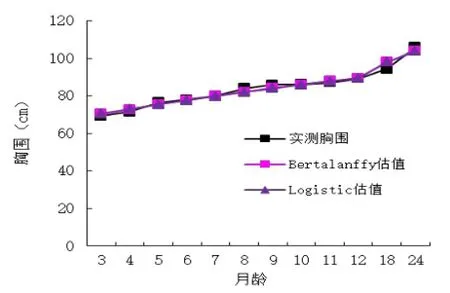
图2 两种生长模式对胸围的拟合

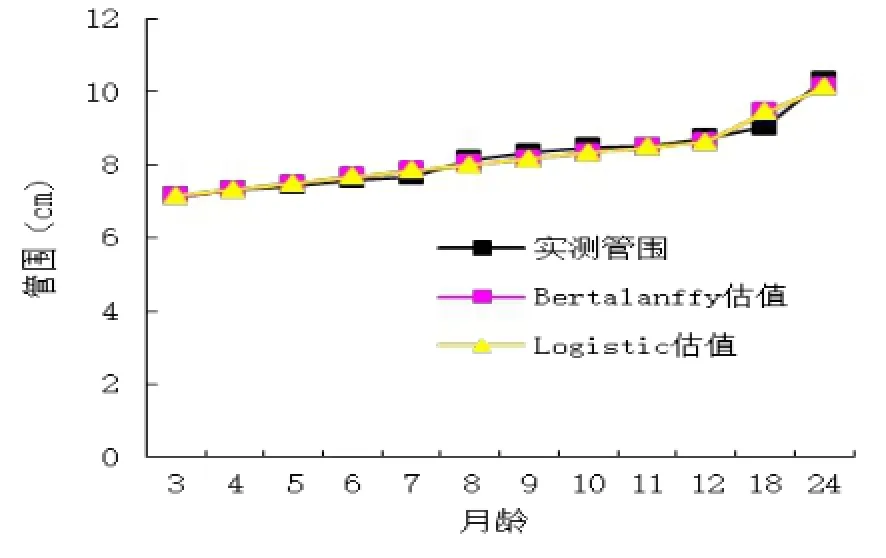
图3 两种生长模式对管围的拟合

图4 两种生长模式对十字部高的拟合

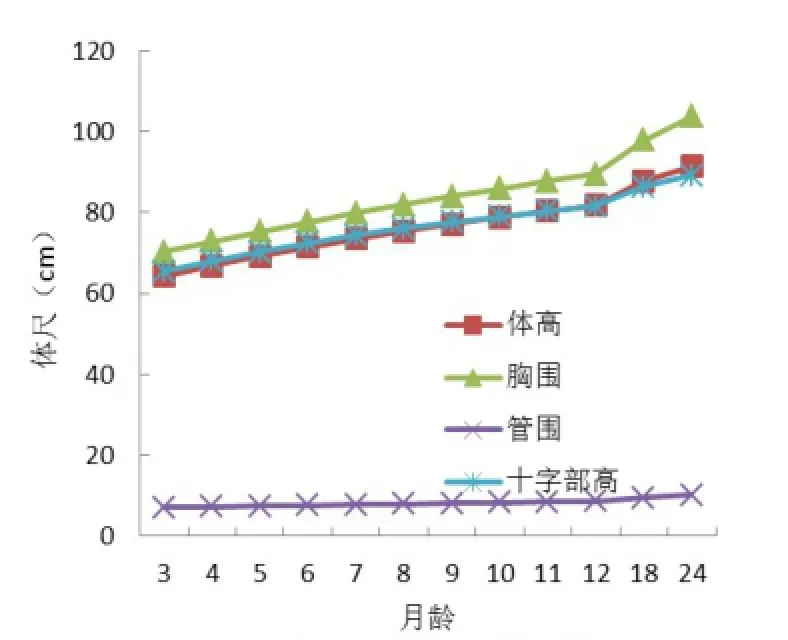
图5 豫北小尾寒羊累积生长曲线

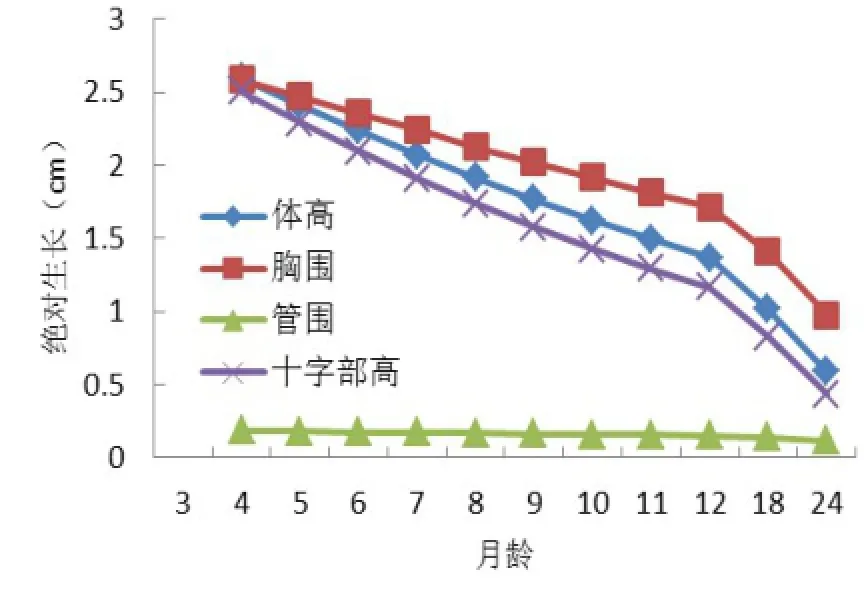
图6 豫北小尾寒羊绝对生长曲线

图7 豫北小尾寒羊相对生长曲线

2.3 生长发育指标计算结果

根据von Bertalanffy模型分别计算出各月龄理论体尺（L），然后依据理论体尺计算出绝对生长（G）和相对生长（R）指标见表4。累积生长曲线见图5，绝对生长曲线见图6，相对生长曲线见图7。

从图5可以看出，4种体尺的生长是较为均衡的，而体高和十字部高的生长趋势更接近，胸围的生长速度有加快的趋势，管围的生长变动较小，这是小尾寒羊体体躯生长特点决定的。由表4和图6可以看出，豫北小尾寒羊4种体尺的生长高峰期均在3～4月龄，以后生长量逐渐下降，且体高的绝对生长曲线与胸围相比下降幅度较大，而管围的绝对生长曲线变化比较平缓。绝对生长曲线中12月

龄之后急剧下降是由于生长期延长的结果。由表4和图7可以看出，4种体尺的相对生长速度在4月龄之后呈持续下降趋势，且体高的相对生长曲线与其他三个体尺相比下降幅度最大，而管围的相对生长曲线变化较为平缓，相对生长曲线中18月龄时的波动是由于测量期拉长所致。

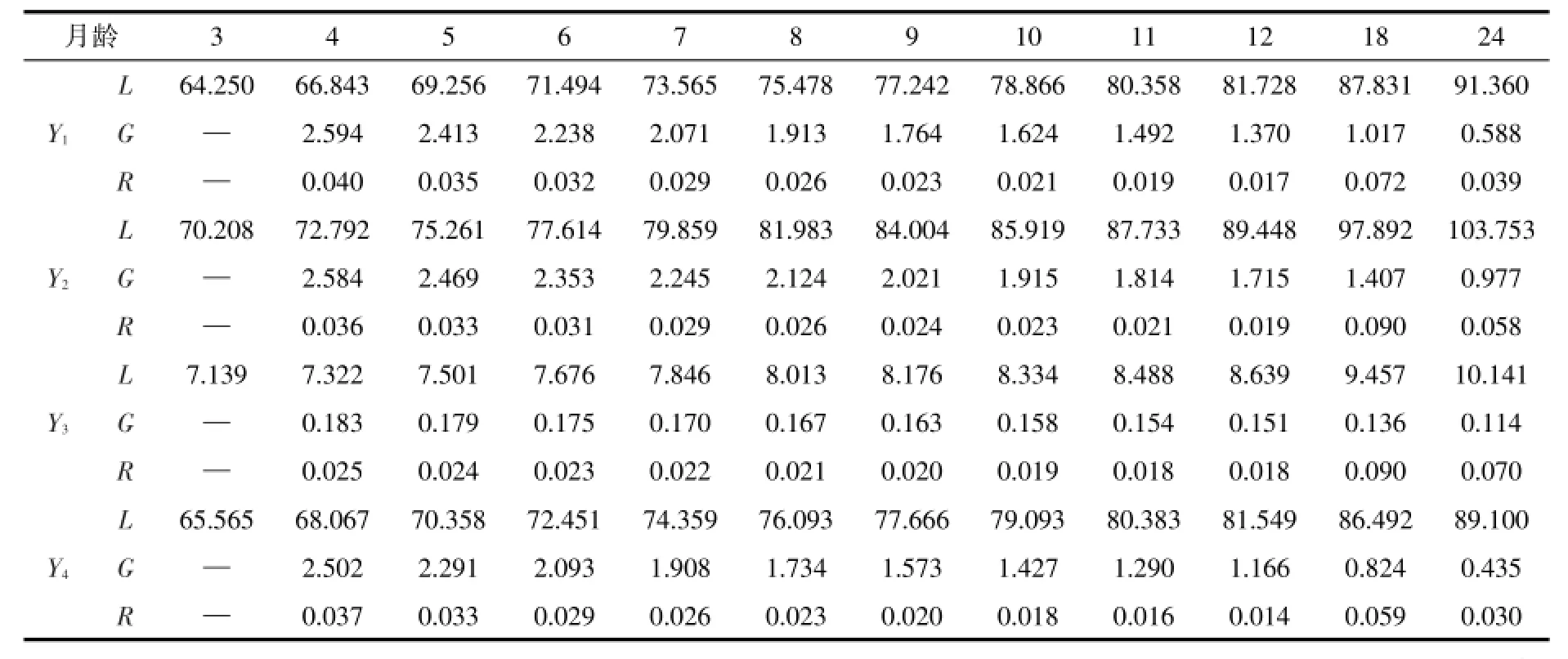
表4 豫北小尾寒羊体尺生长发育指标

3 讨论

3.1 最佳生长模型问题

本研究所使用的Logistic、von Bertalanffy两种模型都是拉伸的“S”形曲线，是拟合畜禽生长发育常用的数学模型，从它们对四种体尺的拟合效果来看，R2值均在0.96以上，从两种模型对4种体尺的拟合比较来看，von Bertalanffy模型拟合效果更好。这一研究结果与梁学武等[10]关于波尔山羊的研究结果不相同，可能是由于羊种不同和生长环境条件的不同造成的。但与马发顺等[12]关于豫北小尾寒羊体重生长规律的拟合结果一致，说明豫北小尾寒羊体尺、体重的生长发育是协调的。本研究仅使用了Logistic和von Bertalanffy两种模型进行模拟，是否还存在更好的数学模型可描述豫北小尾寒羊体尺的生长发育状况有待进一步研究。

3.2 关于生长模型的拐点问题

本研究获得的体尺最佳生长模型为von Berta⁃lanffy模型，但据此未能计算出有效的拐点。分析其原因可能有以下几点：体高、胸围、管围和十字部高这4种体尺的生长发育客观上拐点不明显；小尾寒羊的体重与体尺发育存在着不平衡性，即从幼年期到成年期体重与体尺的发育是不均衡的，所以，体重的生长发育具有明显的拐点，而体尺的生长发育拐点不明确。

3.3 关于生长曲线的形态

理论上的累积生长曲线应呈拉长的“S”形，而绝对生长曲线应呈“钟”形，相对生长曲线应呈拉长的“L”形。但由于本研究区间是3～24月龄，是断奶到成年的阶段，而从出生到断奶的哺乳期并没有测量，所以绘制的累积生长、绝对生长以及相对生长曲线与理论上典型的曲线不完全一致，但大致趋势是符合的，从4种体尺的生长曲线比较来看，虽然整体走向一致，但体尺之间也存在着一定的差异，这也体现出体尺生长发育的不平衡性。

3.4 生长发育的特点

根据von Bertalanffy模型计算的体高、胸围、管围和十字部高的周最大增长量依次为4.157、3.557、0.225和4.554cm·w-1，最大日增长量依次为0.594、0.508、0.032和0.651cm·d-1。这是在特定的环境条件下获得的结果，可作为小尾寒羊相关研究的参考，但在不同条件下，这些数据应谨慎使用。从von Bertalanffy模型对4种体尺的模拟过程来看，4种体尺均在3～4月龄时呈现最快的生长速度，之后生长速度呈现逐渐减慢的趋势，其中体高的生长速度下降幅度最大，其次是十字部高，而管围的减慢幅度最不明显。这些特征可以作为对小尾寒羊饲养管理的参考。

4 小结

本研究运用Logistic和von Bertalanffy两种非线性数学模型分别对豫北小尾寒羊3～24月龄的体高、胸围、管围和十字部高的生长情况进行模拟，拟合结果表明，体高、胸围、管围和十字部高的最佳模型均为von Bertalanffy模型，此模型可较准确地描述豫北小尾寒羊4种体尺的生长发育规律。相应的体尺极限参数A分别为95.932、115.826、13.060和91.896，调节参数B分别为0.168、0.190、0.205和0.149，瞬时相对生长率k分别为0.098、0.069、0.039和0.112。此模型拟合的4种体尺的最大周增长量依次为4.157、3.557、0.225和4.554cm· w-1，最大日增长量依次为0.594、0.508、0.032和

0.651cm·d-1，各体尺之间存在着生长发育的不平衡性，绝对生长和相对生长均符合生长发育的一般规律。

[1]胡永献，李艳凤，郭红星，等.河南小尾寒羊繁殖性能研究报告[J].中国畜牧兽医，2008，35（3）∶136-137.

[2]胡永献，杨家民，李艳凤.河南小尾寒羊裘用性能研究报告[J].中国畜牧兽医，2008，35（6）∶134-135.

[3]胡永献，李艳凤，袁丽，等.河南小尾寒羊肉用性能研究[J].中国畜牧兽医，2008，35（10）∶132-133.

[4]白哈斯.放牧小尾寒羊生长发育的研究[J].中国畜禽种业，2007，3（10）∶74-75.

[5]郭继君.陶寒F1羊和小尾寒羊生长发育的观察[J].中国畜牧兽医，2007，34（9）∶138-139.

[6]胡永献，袁丽，杜勇杰，等.河南小尾寒羊生长发育规律的研究[J].中国畜牧兽医，2008，35（2）∶146-147.

[7]田亚磊，高腾云，白继武，等.河南小尾寒羊体尺与体重的相关性分析[J].中国畜牧兽医，2009（11）∶200-202.

[8]马发顺，王亚楠，常慧，等.豫北小尾寒羊体重体尺间动态相关性研究[J].当代畜牧：下半月，2013（3）∶51-53.

[9]姜勋平，刘桂琼.萨槐杂种山羊生长模型研究[J].黑龙江畜牧兽医，1999（1）∶3-4.

[10]梁学武，刘庆华，陈瑞臻，等.波尔山羊生长模型及体尺体重相关分析[J].中国草食动物，2009（4）∶28-29.

[11]冯敏山，李祥龙.波尔山羊及其级进杂交后代生长模型研究[J].黑龙江畜牧兽医,2003（4）∶1-3.

[12]马发顺，梁秀丽，宋玉伟，等.豫北小尾寒羊生长模型的拟合与分析[J].中国动物保健，2013，15（5）∶12-15.

Simulation on Growth Rule of Yubei Small-tail Sheep Parts Size

MA Fashun1,LI Jinping2,YANG Xin1
(1.Shool of Biotechnology and Food Science,Anyang Institute of Technology,Anyang,455000 China;
2.Anyang City People's Park,Anyang,455000 China)

In order to grasp the growth rule of the parts body ruler about Yubei small-tail sheep.With four kinds of body size of body height,chest circumference,cannon and hip croop height for the material of Yubei small-tail sheep form 3 to 24 months old.The growth process of four kinds body size were fitted and the analysis individual with Logistic and von Bertalanffy.The results showed that the logistic and von Bertalanffy model can describe Yu⁃bei small-tail sheep's actual growth situation well,the goodness of fit were above 0.96,but von Bertalanffy model more in line with the actual growth,better simulation results.the R2were 0.973,0.973,0.965 and 0.977 of four kinds body size of body height,chest circumference,cannon and hip croop height respectively.The correspond⁃ing body size limit parameter A respectively were 95.932,115.826,13.060 and 91.896,adjustment parameter B respectively were 0.168,0.190,0.205 and 0.149,instantaneous relative growth rate k respectively were 0.098, 0.069,0.039 and 0.112,the biggest week growth respectively were 4.157,3.577,0.225 and 4.554 cm·w-1,the greatest daily growth rate respectively were 0.594,0.508,0.032 and 0.651cm·d-1.The von Bertalanffy model was the ideal mathematical model on growth rule of the four kind body ruler of yubei small-tail sheep form 3 to 24 months old.The absolute growth and the opposite growth conform to the growth general rule.These results could be used in feeding yubei small-tail sheep scientifically and also may provide the reference for the following re⁃search.

small-tail sheep;body ruler;growth rule;growth model;fitting

S826

A

1673-2928（2016）06-0085-05

（责任编辑：王彦永）

2016-03-26

马发顺（1963-），男，河南长垣人，安阳工学院生物与食品工程学院教授，研究方向：动物育种理论和动物生长发育规律。