股票市场投资组合策略构造及模型检验
张 力
(中南财经政法大学 金融学院, 武汉 430073)
股票市场投资组合策略构造及模型检验
张 力
(中南财经政法大学 金融学院, 武汉 430073)
股票市场是一个高风险高收益的市场,通过构造投资组合分散风险,可以在一定风险情况下实现收益的最大化或者在收益一定的情况下实现风险最小化.文中从十七个财务因子中提取了八个共同因子进行主成分分析,进而分析沪深A股所有股票的财务状况.通过给每只股票打分,选出前五只股票构造一个投资组合,然后确定各种资产的最优权重和估计出投资组合的VaR,并对VaR进行回测以检验投资组合的可靠性.
股票市场;主成分分析;投资组合;VaR;回测
0 引 言
自从我国股票市场建立以来,经历了大大小小的数次金融危机,由于经济周期和金融危机的存在,股市也经历了牛市和熊市,牛市中基本是买什么股票都是涨的,因此也称为送钱行情,然而在经历熊市时,大多数人都是亏钱的,因此投资组合就显得尤为重要,特别是在2015年熊市显得尤为明显.最著名的证券投资组合理论当属马科维茨投资组合理论,其指的是根据各种证券的风险和收益大小进行适当的组合,以使得在一定风险条件下实现组合利润最大化,或者在一定收益下实现风险最小化.一般而言收益和风险是相互依存的,风险和收益成正相关,因此投资组合的建立就是在收益和风险这一对相互矛盾的统一体中寻找均衡.机构投资者往往具有信息、技术、人才等方面的优势;对于个体户而言往往存在信息不对称、信息闭塞、专业知识不足等原因,很难控制风险,而通过构造投资组合可以帮助个体散户分散规避大部分的非系统风险,并达到自己的预期收益,这对于个体投资者投资金融产品而言具有重要的现实意义.
关于投资组合的构造与分析,国内外学者做了相关研究,贾小波[1]研究了在Beta约束下牛市和熊市两个阶段的最优投资组合;吴丹[2]运用均值方差理论和CAPM模型构造了投资组合,得出投资组合可以有效分散风险和提高收益;王寰[3]运用均值——绝对离差和半绝对离差模型构建了出线性投资组合模型,也能很好的分散风险和提高收益.国外学者R.R.A. Mendes[4]通过计算机运用ARMA-GARCH模型构造多元模型设定特定算法得到相对最优的投资组合;Enriqueta Vercher[5]运用确定性的绝对均值半偏差模型结合VaR构造了最有投资组合;Rubén Saborido[6]运用多目标算法获得模糊投资组合;Vladimir Rankovié[7]运用单均值GARCH VaR的方法构造最优投资组合等等.
1 相关理论介绍
本论文用到了主成分分析方法以及方差-协方差矩阵的相关运算,最后还用到了EXCEL的相关函数来进行选股以及求最优权重和模型的回测.
1.1 主成分分析法
主成分分析又称主分量分析法,它是通过降维的方法将多个指标用少数几个具有代表性的综合指标来替代,并且能保留多个指标的大部分信息并消除原指标可能存在的相关性的一种方法.简称PCA(principal components analysis).
一般为了更加准确的描述事物特征,可能会建立多元回归模型,而在建立多元回归时就不免会在模型中添加较多解释变量,来更准确地反映事物的特征.变量的增加会使得分析变得复杂,也可能存在多重共线性,进而会增加方程在经济含义解释方面的难度.为了解决这些问题,主成分分析法提供了一种降维的思想,其将所有指标的信息通过少数几个指标来反映,而这少数几个指标可以代表大多数变量的信息,这样既可以保持研究的因变量保持原有的特性又可以减少了估计变量的个数和相关性,这就使得估计变得简单,多元回归模型的表达也更为容易.
1.2 马科维茨投资组合理论
证券组合的含义:是指投资者根据证券的风险和收益大小,按一定策略进行选择有价证券组合证券组合,通常包含一揽子有价证券,例如股票、债券等,基金是最典型的投资组合,也指个人或机构投资者所持有的各种有价证券的总称.[8]
1.2.1构建证券投资组合的原因
(1)降低风险.
(2)实现收益最大化.
如何确定不同证券或资产上的投资比例,以使资金稳定快速增长并控制投资风险,这就是投资组合理论要解决的问题.
关于方差协方差法确定权重的问题需要每只股票服从正态分布,这里做出说明,对于单只股票的投资收益率不一定服从正态分布,但是根据中心极限定理,当样本数据足够多的时候,单只股票的投资收益率可以近服从正态分布.(但中心极限定理要求各随机变量互不相关,然而组合中各股票存在一定程度的相关性.)但实证发现,对于一个有效分散化的投资组合,若持有时间不长,其收益率近似地服从正态分布;当持有期限在1个月以上时,其收益率近似地服从对数正态分布.
1.2.2.马科维茨投资组合模型
保持投资组合收益一定的情况下实现风险最小
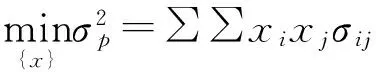
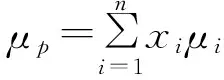
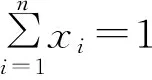


2 投资组合的构造
本论文的数据全部来自国泰安数据库,选择的对象是上海深圳两大证券交易所所有A股股票,由于数据大量的缺失(很多公司都是新上市的),删除了缺失数据,选取的时间段为2005年01月至2015年12月的月度数据,此阶段我国股市经历着牛市和熊市,将数据缺失严重的股票直接删除掉,通过主成分分析法,借助上市公司的财务指标筛选出5只排名靠前的股票构造一个投资组合,分别确定各资产的权重,至此可以确定一个投资组合,对该投资组合使用历史模拟法进行VaR估计和对模型进行回测.
2.1 财务指标的选取
本文选取了十七个财务指标来衡量一个公司是否具有投资价值,选取的指标有X1流动比率、X2速动比率、X3利息保障倍数、X4资产负债率、X5应收账款周转率、X6营运资金(资本)周转率、X7总资产周转率、X8资产报酬率、X9总资产净利润率(ROA)、X10营业利润率、X11息税前营业利润率、X12每股收益、X13息税前每股收益、X14每股营业利润、X15每股净资产、X16每股资本公积、X17每股未分配利润.这十七个指标可以分别代表偿债能力、营运能力、盈利能力、发展能力.
(1)偿债能力,资产负债率是企业负债总额和资产总额的比值,该指标反映了企业的负债情况以及长期偿债能力,一般而言资产负债率越高则偿债能力越差,资产负债率越低则偿债能力越强,但资产负债率过低则不能充分利用外围资金实现自身增长,一般资产负债率在50%左右比较好[10].在本论文中反映偿债能力的指标有资产负债率,流动比率,速动比率,利息保障倍数.
(2)营运能力,营运能力体现的是企业的经营能力,资金的循环和运作,是指企业经营主营业务运用自身资金经营公司实现资金流循环赚取利润的能力.在本论文中衡量企业营运能力的财务指标有:应收账款周转率、营运资金(资本)周转率、总资产周转率等.
(3)盈利能力,稳定的盈利能力是企业保持良好而稳定的持续经营的关键所在,净资产收益率反映了报告期中各种权益要素的综合收益水平.每股净资产是指每股股票对应的净资产份额,其描述的是企业抵御风险的能力[10];在本论文中描述盈利的指标包括资产报酬率、总资产净利润率(ROA)、营业利润率、息税前营业利润率等.
(4)成长能力,主营业务增长率,净利润增长率两个指标主要反映公司未来的成长能力.在实际投资中,成长性好的企业说明其未来发展的空间更为广阔,产生稳定盈利的可能性也就越大.反映成长能力的指标包括每股收益、息税前每股收益、每股营业利润、每股净资产、每股资本公积、每股未分配利润等.
2.2 主成分分析方法的实证应用
主成分分析一般运用于多元回归模型,因为人们为了更准确的描述事物的特征往往会选择更多的变量来对事物的特征进行刻画,但是过多的变量会增加估计的难度,也会使模型变得复杂,这就需要运用主成分分析的方法.在这里从十七个指标中提取八个主成分来代表所有的指标,一般选取累计贡献率大于等于80%则可认为能代表所有变量,这里选出八个指标后累计贡献率达到82.41%,并且每个变量的解释程度大于等于1,并且Kao检验值大于0.5,可进行主成分分析达到降低维数目的.
运用SPSS因子分析可得到成分矩阵,也即每个主成分对应十七个变量线性组合的系数,每一列代表各主成分对应十七个变量线性组合的系数,每一行代表每个变量对各主成分贡献,如下表1所示:

表1 成分矩阵
通过成分矩阵可以得到的各主成分的方程,每一列代表每个主成分以及对应各原始变量的系数,经整理得到的方程如下:
Y1=-0.005X1-0.005X2-0.005X3-0.028X4-0.003X5+0.007X7+0.286X8+0.3X9+0.01X10+0.01X11+0.895X12+0.892X13+0.766X14+0.769X15+0.393X16+0.736X17,
Y2=0.995X1+0.995X2+0.018X3-0.001X4-0.008X7+0.085X8+0.084X9-0.04310-0.043X11+0.011X12+0.009X13-0.001X14-0.035X15-0.033X16-0.021X17,
Y3=0.047X1+0.047X2+0.001X3+0.001X4-0.004X7-0.04X8-0.041X9+0.998X100.998X11-0.005X12-0.003X13+0.008X15+0.01X16+0.00317,
Y4=-0.089X1-0.089X2+0.006X4+0.008X5-0.002X6+0.008X7+0.935X8+0.929X90.045X10+0.045X11+0.026X12-0.005X13-0.107X14-0.299X15-0.234X16-0.22X17,
Y5=0.012X1+0.012X2-0.016X3-0.043X4-0.005X5+0.006X6-0.002X7+0.173X80.181X9-0.001X10-0.001X11-0.334X12-0.33X13-0.39X14+0.531X15X+0.773X16+0.101X17,
Y6=-0.005X1-0.005X2+0.71X3+0.721X4+0.063X5+0.024X6+0.142X7+0.00680.001X9+0.001X12+0.002X13-0.001X14+0.017X15-0.046X16-0.018X17,
Y7=0.004X1+0.004X2-0.117X3-0.086X4+0.693X5+0.14X6+0.708X7+0.001X8+0.0039+0.001X10+0.00111-0.008X12-0.011X13-0.014X14+0.005X15-0.026X16+0.036X17,
Y8=-0.012X3-0.005X4-0.217X5+0.976X6+0.018X7+0.004X12+0.004X13+0.004X14-0.006X15+0.001X16-0.011X17.


表2 前五名股票及其得分
选出的五个公司分别来自不同的行业,有化工新材料、电力、农产品加工、石油矿业开采以及汽车零部件等行业,选取不同行业股票构造投资组合有助于分散风险分散投资,达到控制风险的目的,其次,这五个公司的得分最高,因此从财务来看他们的财务状况较好,说明业绩优异,有较好的潜力,如果当前股票价格偏低则说明是低估的,如果当前的价格偏高则回落的空间也是有限的,因为毕竟有业绩作为支撑[12].
3 投资组合权重的确定
从上述可知,通过研究2005年至2015年沪深A股所有股票的财务数据,选取的十七个因子进行主成分分析,根据均值得分最高挑选出了五只股票,但真正要确定一个投资组合需要确定每只股票投资的比例,也就是每只股票的权重,在最开始的理论部分也提到过马科维茨投资组合理论,他是通过衡量投资组合风险和收益达到最优时的权重,由于本论文选取的数据较多,因此在大样本数据条件下,无论分布是否为正态分布,都可以用正态分布来进行估计.运用上文相关理论中提到的马克维茨投资组合模型,可以确定最优权重.
马克维茨投资组合中的条件运用lingo或者Excel均可以实现,在此调用Excel函数,本论文通过运用EXCEL解决投资组合的一个优化问题,计算各只股票在收益率一定时如何保持最小的风险,本论文用到了MMULT、TRANSPOSE、MINVERSE函数[13],首先选取了2005年至2013年五只公司的收盘价来研究五只上市公司的收益率,首先对五只股票的收益率取对数然后差分,可以得到每只股票的收益率,通过五只股票的收益率可以得出这五只股票的方差-协方差矩阵,如下表3:

表3 五只股票的方差协方差矩阵
注:每个变量的后三位数字是每只股票代码的后三位
通过=MMULT(TRANSPOSE(T3:T7),MINVERSE(O3:S7))/MMULT(MMULT(TRANSPOSE(T3:T7),MINVERSE(O3:S7)),T3:T7),其中T3:T7是一个单位列向量,O3:S7是方差-协方差矩阵,这个函数可以直接求出每只股票的权重,其原理来自马科维茨投资组合理论,通过Excel可以得到每只股票的最优权重如下表4所示:

表4 五只股票的最优权重
所有的权重之和等于1,也就是将自己的资产的17.71%投资于中材科技,资产的21.17%投资威孚高科,资产的18.90%投资于攀钢钒钛,22.67%投资于漳泽电力和19.55%的资产投资东凌粮油,这样在保证一定收益的情况下可以实现风险最小,也就是选取的五只股票的最优线性组合,而这五只股票是通过主成分分析,通过一系列的财务数据分析得出的,因此也是相对绩优股的最佳搭配,既可以实现收益的相对较大,也可以实现这五只股票投资组合的风险最小.即使经历股灾,但是有业绩作为保证,那么长期持有最终也是会盈利的.
4 投资组合模型的估计及模型回测
风险价值 (ValueatRisk)简称VaR,也称为 “受险值”,其含义是指正常情况下下,金融资产组合持有一段时间,在一定的置信水平下可能发生的最大潜在损失.但VaR无法描述出在置信水平外发生的最大损失为多少,所以它是一种右侧描述,它要求有持有期和置信水平,持有期越长潜在发生损失的可能性越大,同样的置信水平越高,VaR值也越大.
一般估计VaR有三种方法,方差-协方差法,历史模拟法,蒙特卡洛模拟法.在此用历史模拟法进行估计VaR,历史模拟法操作简单,便于观察,运用Excel就可以操作,通过上述五只股票的交易数据以及各自占的权重可以计算出这个投资组合的收益率,然后将投资组合的收益率按照从小到大的顺序进行排序[14],由于做VaR时选取的时间段为2005年至2013年,在99%的置信水平下对1693个收益率排序估计VaR的对应的收益率为-0.045173137(1693×1%=16.93,按从小到大数投资组合的第十七个收益率即VaR),即1000万按五只股票的权重进行投资,一天内有99%的把握会亏损不会超过45.173万,即 1000万一天对应的VaR为45.173万,如何检验这个VaR是否可靠需要对这个VaR进行回测[15].
进行回测的数据选取五只股票2014年至2015年的收盘价数据,依然按照上述五只股票的权重进行投资,然后计算出投资组合的收益,同样利用历史模拟法,持有一天在99%的置信水平下对应的损失为-0.043168589<-0.045173137=VaR,或者从2014年至2015年投资组合的收益中找出收益率小于-0.045173137的天数,累计起来再除以总天数和1%进行比较,如果这个比例大于1%则说明原模型预测不那么可靠,偏离越大越不可靠,若小于1%则说明原模型的VaR是可靠的,投资组合也是可行的,通过记录2014年至2015年投资组合中损失超过VaR的个数为两个,而所有组合的天数318个,比例为0.63%<1%,也就是这个损失并没有超过上述估计出的VaR,因此模型是可靠的.
5 结论与展望
通过十七个财务指标从沪深A股中选取五只股票来构造一个投资组合,再利用大样本数据结合马科维茨投资组合理论,运用方差协方差矩阵来确定在一定收益下最小方差投资组合各股票的权重,通过确定投资组合的权重就可以构造一个最优的投资组合,构造投资组合后估计出投资组合的VaR,利用VaR可以描述投资组合面临的风险,进而对确定的VaR通过未来产生的投资组合收益进行检验,检验确定的最大潜在损失是否可靠.在实证研究的整个过程中所用的数据均来自国泰安数据库,模型构造严格根据指标的得分进行筛选,最后投资组合的潜在最大损失VaR也通过了检验,说明投资组合构造策略是严格和成功的.
论文投资组合主要运用一系列的财务指标来进行筛选投资组合的,考虑的更多是会计层面,也可以加入其他非财务指标来决策,一般而言股票市场受很多因素的影响,因此考虑的越多越全,构造的投资组合可能就越准确,如果将实际市场面临的其他因素加入其中,效果会更好.随着数据越来越全,越来越公开,越来越准确,通过构造投资组合来进行投资将会是大势所趋,类似于基金经理的投资,散户炒股的现象会越来越少,或者散户运用构造出的专业投资组合进行投资,或者委托投资代理商进行投资,与基金市场类似,这些专业的投资者或者机构将会运用更专业的知识去管理资金,金融市场会更加趋于稳定.
[1]贾小波.Beta约束下的投资组合最优化分析[D].电子科技大学, 2014.
[2]吴丹.中国股市最优投资组合构造及风险分析[J].现代物业旬刊, 2010, 9(1):16-17.
[3]王寰.可线性规划的证券投资组合模型及其应用[D].南京农业大学, 2008.
[4]MendesR.R.A.,PaivaA.P.,PeruchiR.S.,etal.MultiobjectiveportfoliooptimizationofARMA-GARCHtimeseriesbasedonexperimentaldesigns[J].Computers&OperationsResearch, 2015, 66.
[5]VercherE.,BermúdezJ.D.Portfoliooptimizationusingacredibilitymean-absolutesemi-deviationmodel[J].ExpertSystemswithApplications, 2015, 42(20):7121-7131.
[6]SaboridoR.,RuizA.B.,BermúdezJ.D.,etal.EvolutionaryMulti-objectiveOptimizationAlgorithmsforFuzzyPortfolioSelection[J].AppliedSoftComputing, 2015, 39:48-63.
[7]RankoviĉV,DrenovakM,UrosevicB,etal.Mean-univariateGARCHVaRportfoliooptimization:Actualportfolioapproach[J].Computers&OperationsResearch, 2016, 72: 83-92.
[8]向骏文.基于马科维茨投资组合理论的股票投资策略[J].中国证券期货, 2012(8):202-202.
[9]屠新曙,王春峰.最佳均值VaR投资组合问题的研究[J].湘潭大学自然科学学报.2002,24(2),1-5.
[10]邓天石.基于均值-CVaR投资组合优化模型实证分析[D].重庆大学, 2014.
[11]胡经生,王荣,丁成.VaR方法及其拓展模型在投资组合风险管理中的应用研究[J].数量经济技术经济研究, 2005, 22(5):141-150.
[12]邢灵博.多元马氏模型状态空间的基本性质及其分解定理[J].琼州学院学报, 2014, 21(2):15-18.
[13]曹茂林.层次分析法确定评价指标权重及Excel计算[J].江苏科技信息, 2012(2):39-40.
[14]张顺.VaR的计算方式及其回测检验——基于计算机产业股票的实证研究[J].吉林省经济管理干部学院学报, 2012, 26(2):61-64.
[15]周敦辉,王路.基于GARCH模型的VaR方法对中国股市风险的实证分析[J].琼州学院学报, 2015, 22(5):103-109.
(编校:曾福庚)
Constructing Stock Market Investment Portfolio Strategy and the Model Test
ZHANG Li
(School of Finance, Zhongnan University of Economics and Laws, Wuhan 430073, China)
The stock market is a high-risk and high-yield market. With rational hypothesis and under the consideration that people are risk-averter, the present research constructed a portfolio to spread risk, to maximize earnings under a certain risk or to achieve risk minimization with certain returns. Due to that the risk of stock market is huge, constructing a portfolio is especially important. This current paper has undertaken the principal component analysis of eight common factors extracted from seventeen financial factors, through which all the stocks’ financial condition of Shanghai and Shenzhen A shares were analyzed. By marking each stock, the top five stocks were selected to construct a portfolio. Then, the optimal weights of the five stocks were achieved to estimate the portfolio’s VaR. And the reliability of the portfolio was attested through back-testing of VaR.
the stock market; principal component analysis; portfolio; VaR; back-testing
2016-03-10
张力(1990-),男,湖北孝感人,中南财经政法大学金融学院,2014级金融学专业硕士研究生,研究方向为金融风险管理及其定价.
F830.91
A
1008-6722(2016) 05-0108-06
10.13307/j.issn.1008-6722.2016.05.21

