蛇形机器人伸缩运动性能研究①

卢振利 谢亚飞 张国栋 张 凯 刘 超 冯大宇 李 斌

(*常熟理工学院电气与自动化工程学院 常熟 215500)(**中国科学院沈阳自动化研究所机器人学国家重点实验室 沈阳 110014)(***常熟理工学院汽车工程学院 常熟 215500)(****中国矿业大学信息与电气工程学院 徐州 221116)(*****阿威罗大学电子和信息通信工程研究所 阿威罗 3810-193，葡萄牙)(******大连国通电气有限公司 大连 116650)



蛇形机器人伸缩运动性能研究①

卢振利②********谢亚飞*****张国栋******张 凯***刘 超*冯大宇*李 斌**

(*常熟理工学院电气与自动化工程学院 常熟 215500)(**中国科学院沈阳自动化研究所机器人学国家重点实验室 沈阳 110014)(***常熟理工学院汽车工程学院 常熟 215500)(****中国矿业大学信息与电气工程学院 徐州 221116)(*****阿威罗大学电子和信息通信工程研究所 阿威罗 3810-193，葡萄牙)(******大连国通电气有限公司 大连 116650)

为研究蛇形机器人常用的典型步态——伸缩运动的性能与不同摩擦系数环境的关系，分别用单向被动轮和双向被动轮设计正交串联蛇形机器人地面接触机构。通过蛇形曲线公式控制蛇形机器人垂直关节节律实现伸缩运动。通过实验得出了摩擦系数对单向被动轮和双向被动轮接触面型蛇形机器人伸缩运动步态的影响及对应的蛇形曲线参数的调节策略。

蛇形机器人, 单向被动轮, 双向被动轮, 摩擦系数, 伸缩运动

0 引 言

蛇形机器人是模仿蛇细长无肢的身体设计而成。重心低以及和地面有多个接触点，使蛇形机器人在环境适应性方面优于轮式机器人和腿式机器人[1]。蛇形机器人的研究在国内外引起高度关注，由于机构设计、控制方法日趋成熟，因而蛇形机器人应用成为必然[2,3]。蛇形机器人在不同环境中的运动性能实验和分析是实现蛇形机器人实用化的基石。研究环境摩擦系数和蛇形机器人运动性能关系的工作往往集中在重单体在不同控制策略下的运动效果。 关于伸缩运动，国内中科院沈阳自动化研究所从仿生学角度探究了蛇在不同环境下的伸缩运动，给出了实现垂直伸缩和水平伸缩运动的机理和运动产生方法，但未给出具体环境下伸缩运动的性能。该研究从概念上给出了单线被动轮实现机理，而未进行相关机构设计[4]。

本研究使用单被动轮和双向被动轮分别构成了正交串联蛇形机器人的接触结构。通过蛇形曲线控制该机器人实现伸缩运动步态，研究了不同地面与接触机构摩擦系数对步态的影响及步态参数调节策略，而且对使用单向轮和双向轮的蛇形机器人在进行伸缩运动中的性能进行了研究。

1 蛇形机器人接触机构设计

蛇可以用不同的节律运动来适应环境，例如在树干上通过节律伸缩自己的躯体，实现攀爬，如图1所示。典型的伸缩运动如图2所示。

本设计中蛇形机器人本体采用正交串联关节构成，如图3所示。通常采用双向被动轮，如图4所示，改变纵横向摩擦比实现蜿蜒运动。

图1 蛇在树干上运动

图2 典型的伸缩运动

图3 蛇形机器人

图4 双向被动轮接触机构

图5 单向被动轮接触机构

图6 蛇形机器人

相较于双向轮既可顺时针转动也可逆时针转动，单向轮却只能沿其中一种方式转动，更贴近生物蛇的鳞片单向制动特性。

二者均采用同样的控制策略来实现伸缩运动。控制系统采用Arduino单片机进行运动规划，之后通过串口把垂直关节的转动角度发到电机控制器，电机控制器直接驱动各个电机转动，带动机器人本体实现设定的动作，见文献[5]。

2 伸缩运动控制

2.1 节律生成

伸缩运动的节律和蜿蜒运动类似，换言之，蜿蜒运动是水平关节摆动，带动身体运动，伸缩运动是垂直关节的运动带动身体运动。二者的节律是相同的，只是作用的对象空间不同。同样可以采用日本东京工业大学Hirose教授提出的蛇形曲线公式[6]控制机器人实现伸缩运动，对应的垂直电机节律公式如下：

βi(s)=-2αsin(knπ/N)[sin(2knπs/L+2knπi/N)]

(1)

其中βi(s)为第i个垂直关节电机转角；i=1,…8,为电机号；π=3.1415926；α为起始弯角；kn为S形曲线个数；L为机器人总长度；N为机器人总节数。改变变量s的变化率δs可以改变蛇形机器人的前行速率。

2.2 α变化对蛇形机器人伸缩运动的影响

改变式(1)中参数α和kn的值，研究该参数对蛇形机器人伸缩运动波形和运动的影响。选取接触机构为双向被动轮的蛇形机器人来做此实验。在实验背景中选取一块竖直放置的长木板作为参考对象，板上两条竖直红线之间的距离为1m作为蛇形机器人实验运行参考距离。实验如下：

(1)当α=0.1、kn=2时，蛇形机器人以2个S波形进行伸缩运动，前进速率约为0.0045m/s, 实验过程如图7所示。

(2)当α=0.2、kn=2时，前进速率约为0.011m/s，实验过程如图8所示。

首先使用乙醚将实验大鼠麻醉，选定胸正中为手术区域，去毛备皮消毒，做好关闭胸腔的荷包缝合准备，之后沿锁骨正中线做2 cm纵向切口切开皮肤，在第四或第五肋间将大鼠胸部肌肉进行钝性分离，使胸骨、肋骨充分暴露，将胸腔打开，心包剪开，在胸廓轻轻按压以将大鼠心脏挤出。使用无创性缝合线在动脉圆锥与左心耳之间冠状静脉处进行冠状动脉的结扎，之后将心脏迅速放回原位，将胸腔气体挤出，并迅速将缝合线拉紧，将胸腔逐层进行关闭，将外皮缝合好，保证开胸时间＜60 s。

(3)当α=0.3、kn=2时，前进速率约为0.018m/s,实验过程如图9所示。

(a) t=0s

(b) t=90s

(c) t=220s

(a) t=0s

(b) t=30s

(c) t=95s

(a) t=0s

(b) t=30s

(c) t=55s

(4)当α=0.4、kn=2时，实验过程如图10所示。

(a) t=0s

(b) t=23s

(c) t>24s

根据上述改变蛇形曲线参数α的实验，在机械结构允许且能完整实现伸缩运动的前提下，改变变量α的值，从而可以改变蛇形机器人的S形曲线的弧度，α越大，S波幅值越大，运动速率越大，蛇形机器人的前进速率V与起始弯角α的关系曲线如图11所示。其中α=0.4该机器人伸缩运动出错，因为硬件条件限制使α值再加大时将导致机器人出现故障及原件损坏。所以α=0.4可看作该蛇形机器人样机伸缩运动的最大起始弯角。

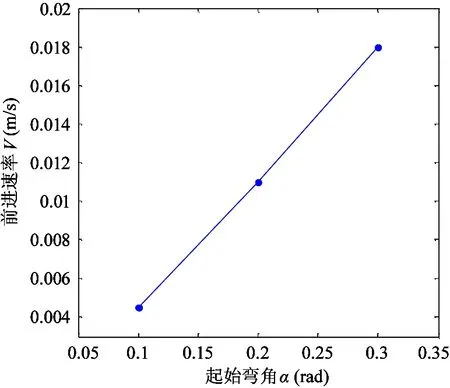
图11 α与V关系曲线

2.3 kn变化对蛇形机器人伸缩运动的影响

改变蛇形曲线参数kn的值，从而改变了蛇形机器人体内S波个数。通过观察不同S波个数形态下的蛇形机器人伸缩运动，得出只在变化蛇形曲线参数kn的情况下，蛇形机器人伸缩运动的前进速率V与kn的关系。实验如下：

(1)当kn=1.5、α=0.2时，蛇形机器人以1.5个S波形进行伸缩运动，前进速率约为0.029m/s, 实验过程如图12所示。

(2)当kn=2、α=0.2时，蛇形机器人以2个S波形进行伸缩运动，前进速率约为0.011m/s, 实验过程如图13所示。

(a) t=0s

(b) t=20s

(c) t=35s

(a) t=0s

(b) t=30s

(c) t=95s

(3)当kn=2.5、α=0.2时，蛇形机器人以2.5个S波形进行伸缩运动，前进速率约为0.0095m/s, 实验过程如图14所示。

(a) t=0s

(b) t=60s

(c) t=105s

从变化蛇形曲线参数kn的伸缩运动实验中可看出，由于自身机构的限制，在kn变化合理的范围内，蛇形机器人伸缩运动的前进速率随着体内S波的增大而减小。kn与前进速率V的关系曲线如图15所示。

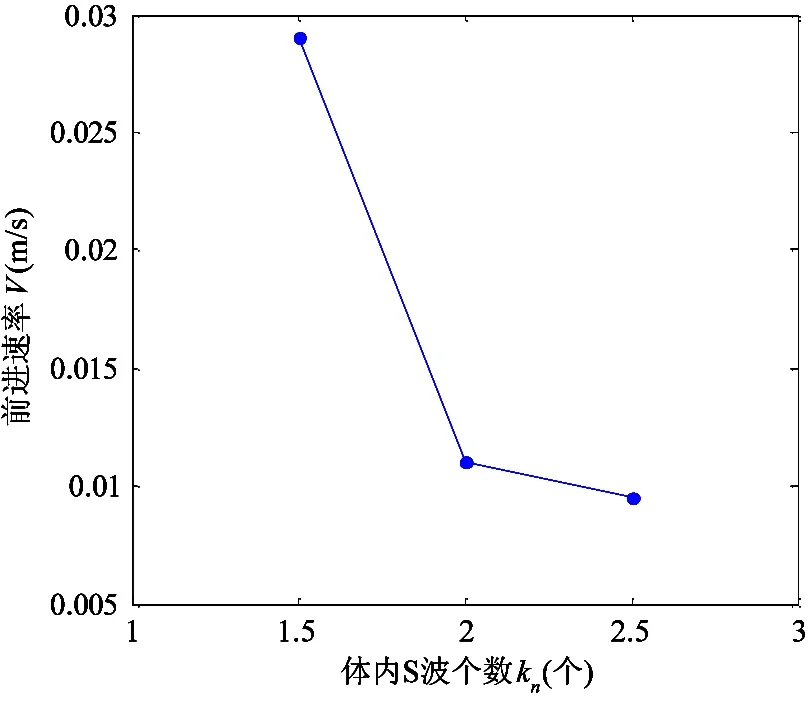
图15 kn与V的关系曲线

3 伸缩运动与摩擦系数关系实验

实验设定机器人伸缩运动行进相同距离，采用单向被动轮型和双向被动轮型蛇形机器人，在相同的控制指令下完成对应的动作，进行运动性能对比。

3.1 摩擦系数对蛇形机器人伸缩运动步态的影响

研究了蛇形机器人伸缩运动与摩擦系数之间的关系，选取一组蛇形曲线参数，如表1所示。

表1 蛇形曲线参数表

应用具有不同摩擦系数材质做成的胶带粘附在被动轮表面，模拟不同摩擦系数环境来进行实验。实验中离竖直木板较近的是单向轮蛇，较远的则是双向轮蛇，具体实验如下所示：

实验一 透明胶带贴合：此时μ(滚动)=0.0487，实验过程如图16所示。

(a) t=0s

(b) t=20s

(c) t=38s

(a) t=0s

(b) t=20s

(c) t=35s

(a) t=0s

(b) t=20s

(c) t=30s

实验二 橡胶胶带：此时μ(滚动)=0.0769，实验过程如图17所示。

实验三 铁砂胶带：此时μ(滚动)=0.1154，实验过程如图18所示。

据上述不同摩擦系数对伸缩运动影响实验，得出数据如表2所示。

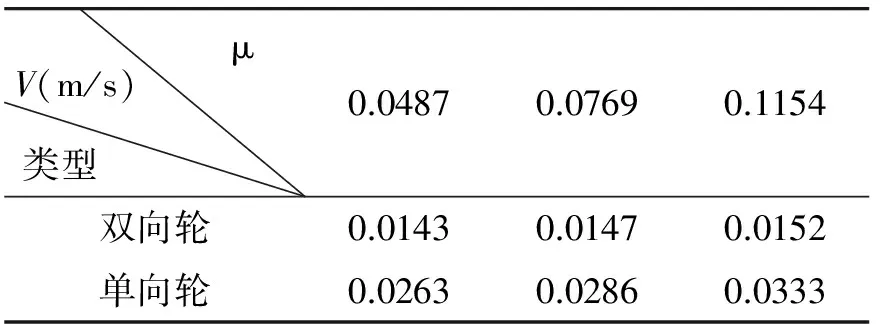
μV(m/s)类型0．04870．07690．1154双向轮0．01430．01470．0152单向轮0．02630．02860．0333

3.2 实验分析

上述实验表明：随着摩擦系数μ的增大，蛇形机器人的前行速率V增大。

基本结论如下：蛇形伸缩运动双向轮蛇形机器人前行摩擦系数μ与速率V之间的关系如图19所示；单向轮蛇形机器人摩擦系数μ与速率V之间的关系如图20所示。

实验表明：单向被动轮型接触结构的蛇形机器人的运动速率在相对应的摩擦系数下要高于双向被动轮型蛇形机器人。

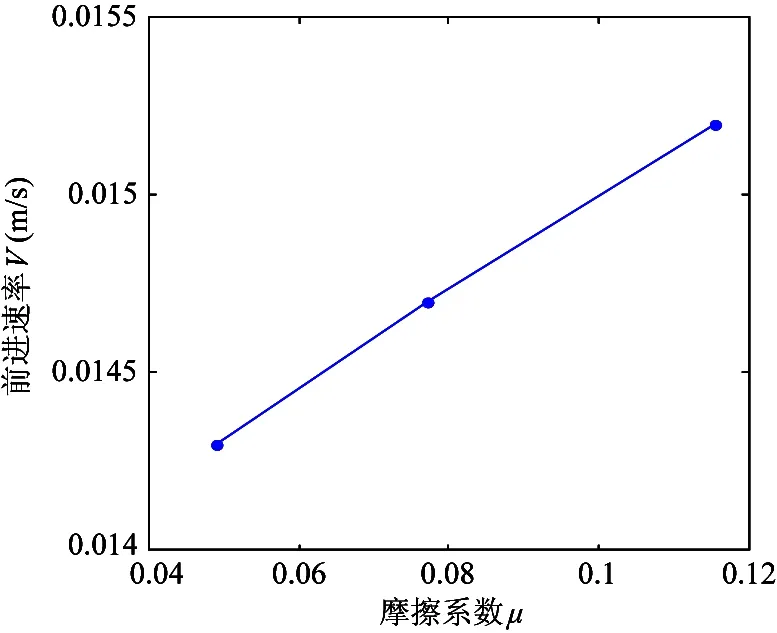
图19 双向轮μ与V关系曲线

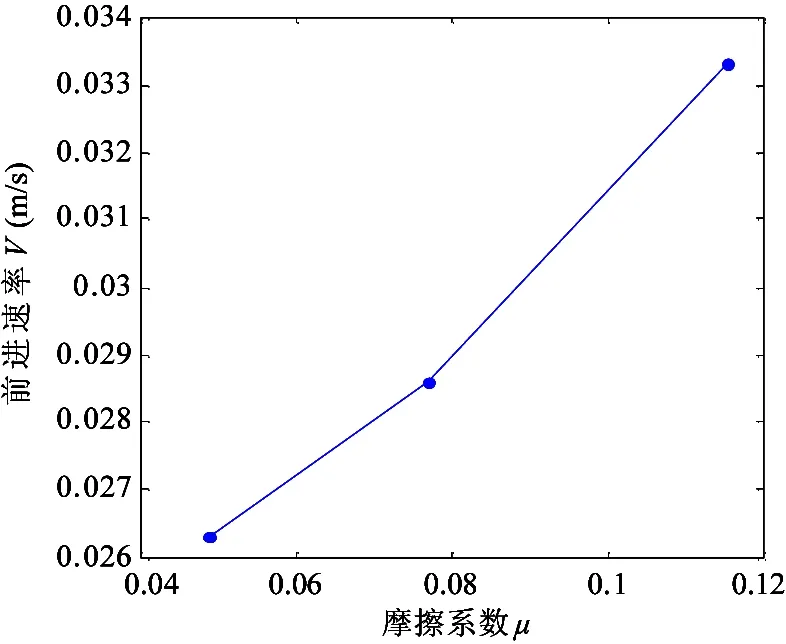
图20 单向轮μ与V关系曲线

4 结 论

本文通过正交连接关节构成蛇形机器人，针对单向被动轮和双向被动轮作为接触机构分别进行了伸缩运动性能研究。通过蛇形曲线公式控制蛇形机器人伸缩运动的垂直关节运动节律。通过实验研究了蛇形曲线起始弯角α和S波个数kn对蛇形机器人伸缩运动的影响；粘贴不同介质，改变被动轮与地面间的摩擦系数，针对不同摩擦系数环境对蛇形机器人伸缩运动进行实验，得出摩擦系数μ与伸缩运动速率V与之间的关系。

[1] 叶长龙，马书根，李斌等. 蛇形机器人的转弯和侧移运动研究. 机械工程学报，2004,40(10):119-128

[2] 刘华，颜国正，丁国清．仿蛇变体机器人运动机理研究．机器人，2002，24(2)：154-158

[3] 张玲玲，曲泽超.蛇形机器人的机构设计及运动分析. 机电工程，2012,29(5):512-515

[4] 刘金国，王越超，李斌等. 蛇形机器人伸缩运动仿生研究. 机械工程学报，2005,41(5):108-113

[5] 卢振利,刘超,谢亚飞等. 蛇形机器人的设计及摩擦力对其运动性能影响的分析, 2015,3: 293-299

[6] Hirose S. Biologically Inspired Robots (Snake-like Locomotor and Manipulator). Oxford: Oxford University Press， 1993

Study on concertina locomotion performance of a snake-like robot

Lu Zhenli********, Xie Yafei*****, Zhang Guodong******, Zhang Kai***, Liu Chao*, Feng Dayu*, Li Bin**

(*School of Electrical Engineering and Automation, Changshu Institute of Technology, 215500 Changshu)(**State Key Laboratory of Robotics, Shenyang Institute of Automation, CAS, Shenyang 110014)(***School of Automotive Engineering, Changshu Institute of Technology, Changshu 215500)(****School of Information and Electrical Engineering China University of Mining and Technology, Xuzhou 221116)(*****Institute of Electronics and Telematics Engineering of Aveiro,University of Aveiro, Aveiro 3810-193, Portugal)(******Dalian Guo Tong Electric Co., LTD, Dalian 116650)

In order to study the relationship between the performance of a snake-like robot’s concertina locomotion and the friction coefficient, the ground contact mechanisms of orthogonal series snak-like robots were designed by using the unidirectional passive wheel and the bidirectional passive wheel, respectively. The serpenoid curve formula was used to control the rhythm of vertical joints to realize the concertina locomotion. The influence of the frictional coefficient on the concertina locomotion gait of the robot using unidirectional passive wheel and the robot using bidirectional passive wheel, as well as the corresponding parameter adjustment strategies of the serpenoid curve formula, were found through aseries of experiments.

snake-like robot, unidirectional passive wheel, bidirectional passive wheel, frictional coefficient, concertina locomotion

10.3772/j.issn.1002-0470.2016.04.008

①国家自然科学基金(61333016)，机器人学国家重点实验室开放基金(2014-O08)，校新引进教师科研启动项目(XZ1306)和葡萄牙科技部基金(CIENCIA2007)资助项目。

2015-08-10)

②男，1974年生，博士，硕士生导师；研究方向：机器人智能控制；联系人，E-mail: zhenlilu@cslg.cn(