集合神经网络的洪水预报

江衍铭, 张建全, 明 焱

(1.浙江大学 建筑工程学院水文与水资源工程研究所 浙江 杭州 310058;2.浙江大学 建筑工程学院建筑学系 浙江 杭州 310058)



集合神经网络的洪水预报

江衍铭1, 张建全1, 明 焱2

(1.浙江大学 建筑工程学院水文与水资源工程研究所 浙江 杭州 310058;2.浙江大学 建筑工程学院建筑学系 浙江 杭州 310058)

针对防洪减灾的问题,通过将集合预报概念应用于人工神经网络,综合考虑样本和参数等因素的影响,构建集合神经网络模型,以降低单一神经网络模型的不确定性.针对初始值扰动和样本重采样两方面分别产生集合成员,由简单平均和贝叶斯模型加权平均整合预报输出,构建龙泉溪流域预见期为1～3 h的集合洪水预报.结果表明,相对于单一神经网络,集合神经网络模型有效地提高预测的精度.从均方根误差上看,集合神经网络模型性能比单一神经网络模型提升了15%～35%.在众多集合策略中,以初始值扰动和简单平均操作最简单,模型预报输出有16%～32%的提升,重采样和贝叶斯模型加权平均的组合效果使预报精度改进了22%～35%.

洪水预报；人工神经网络(ANN)；贝叶斯模型加权平均(BMA)；集合预报

洪水预报是国内外备受关注的议题,也是水利防灾事业发展上的主要趋势之一.近年来,受到全球气候变化的影响,水文极端事件的频率和影响程度呈上升趋势.因此,构建有效的洪水预报模型,具有强烈的紧迫性和必要性.人工神经网络应用于水文相关的研究,如城市用水量、洪水预/警报、河流生态健康预警等已经得到了充分的发展,并取得了不错的成果[1-5].然而,人工神经网络对样本噪声、网络参数、网络模式等因素的敏感性,限制了它的应用和发展[6-7].近年来,集合概念引入水文预报的研究日益增加且效果显著.包红军等[8]基于集合预报构建淮河流域多模式集合洪水预报模型,延长了洪水预报预见期72～120 h.孙照渤等[9]引入交叉检验及集合预报思想,在一定程度上降低了人工神经网络单一预报的随机性,改进了预报效果.Kasiviswanathan等[10]使用遗传算法获得一组较佳的初始值以产生集合成员,结果表明,相较于单一神经网络,集合神经网络显著提高预报精度.El-Shafie等[11]指出单一神经网络在训练阶段易出现过拟合问题而失去泛化能力,针对模型结构方面构建集合神经网络以预测潜在蒸散量,结果表明,集合神经网络优于传统的单一神经网络.但是,以集合概念或方法应用于神经网络的研究较少,且尚未有关于集合神经网络方法较详细的介绍.

目前最热门的集合神经网络方法,是对初始值细微扰动,产生多组不同的初始参数进行多次重复的计算并从中抽取有用信息.人工神经网络模型受样本序列的质量和数量影响较大,可以通过重采样方法产生多组样本以训练得到不同的最优参数,再进行有效整合以达到对样本“降噪”.本文拟用初始值和重采样技术产生集合成员,使用简单平均和贝叶斯模型加权平均(bayesian model average,BMA)整合集合成员[12-13],构建龙泉溪流域的集合流量预报.

1 方 法

1.1 集合神经网络概述

洪水通常呈现暴涨暴落的特性,变化时间快,使洪水预报成为水利防灾领域中一大难点和热点.洪水预报的关键在于把握洪水发生时的涨落规律,神经网络可以通过历史观测数据有效地建构水文系统输入与输出之间的映射关系,对于复杂的水文机制能够通过历史数据训练对水文现象进行预测.集合神经网络的概念是将集合方法的概念引入神经网络中,集合方法的原理是对某一特定目标建构多组(即集合成员)不同的输出结果,而各输出的差异可提供有关被预报量的概率分布信息.以往有关人工神经网络的研究表明,不确定性来源可分成数据的不确定性、自变量选取的不确定性、模型的不确定性(包括初始值、参数、模式).集合预报技术目前已发展到考虑模式初始值的不确定性和模式架构的不确定性,避免单一确定性结果易存在的预报误差.此特点正好弥补神经网络对于初始值等的敏感性.集合神经网络的构建可分为2大步骤：产生集合成员和整合集合成员.产生集合成员的方法主要包括初始值的扰动、神经网络结构的扰动、训练算法的扰动、神经网络模式的扰动、训练数据组的扰动,整合集合成员的方法主要包括简单平均、stacking平均、贝叶斯模型加权平均[13-14].本文的集合策略拟采用初始值的扰动、训练数据组的扰动与简单平均、贝叶斯模型加权平均的组合.训练数据组的扰动方法,包括bagging算法和boosting算法.

1.2 重采样算法

1.2.1 Bagging算法 bagging算法重采样的原理是对原始训练数据组的数据等可能地抽取一定次数,产生新的训练数据组.假定原始训练数据组T包含N笔数据[x1,y1],…,[xN,yN],x和y分别为输入和输出变量.数据组T中的每笔数据的概率都是1/N.在此概率分布上,对原始训练数据组T重采样一定次数,产生新的训练数据组TB.

1.2.2 Boosting算法 boosting算法重采样的原理是产生一组神经网络模型序列,通过对数据组的每笔数据都标定一个概率(在模型训练过程中发生变化),以使得每个神经网络模型更加关注前一个模型未模拟好的数据.概率更新规则详见如下Adaboost.R2算法.训练数据组T中第i笔训练数据在第s步的概率是Ds(i),算法步骤如下：

1)概率初始化：设s=1

D1(i)=1/N,i=1,2,…,N.

(1)

2)基于概率分布Ds,对原始训练数据组T进行重采样,产生新的训练数据组TS.

3)使用训练数据组TS,训练得到新的神经网络模型ks.

4)计算模型的最大误差Lmax

Lmax=sup (|ks(xi,y)-yi|),i=1,2,…,N.

(2)

5)计算训练数据组中每笔样本的误差Li

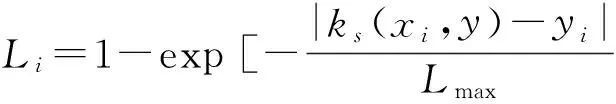
(3)

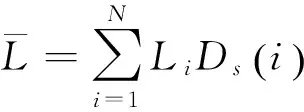
(4)

7)计算系数Bs

(5)

8)更新概率分布Ds

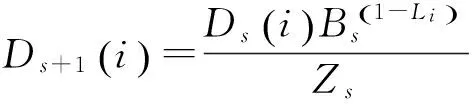
(6)

式中：Zs为归一化因子,以使得Ds+1是一个概率分布.

9)S=S+1；

Bagging算法和boosting算法的区别在于训练数据组的数据分布是否根据前一个网络模型的性能发生变化.Bagging算法是随机地改变数据分布,而boosting算法是有侧重地改变数据分布.在大多数应用中,boosting算法要比bagging算法更有效,但是后者在训练集合神经网络也具有一定优势.

1.3 整合方法

通常情况下,简单平均(mean)公式如下：

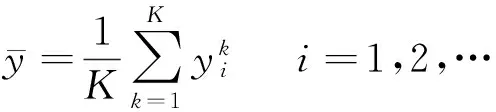
(7)

但是,Drucker(1997)认为,此平均方法不适合由Adaboost.R2算法产生集合神经网络模型.可以通过加权中值方法,来整合集合神经网络[15].公式如下：

Ofinal=

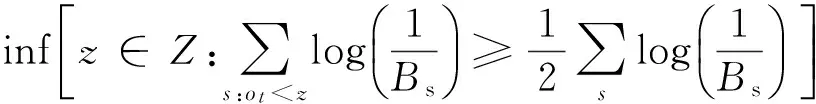
(8)

式中：对于某一特定输入i,每个预测Os(yi,z)对应一个系数Bs,Ofinal为经整合后模型输出.Bs是通过式(5)来计算.

(9)

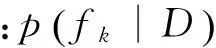
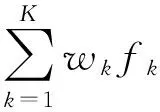
(10)

(11)

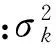
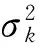
2 精度指标

关于洪水预报好坏的评定指标通常采用确定性系数、洪峰合格率等.除此之外,本文拟采用均方根误差(root mean square error,RMSE)、Gbench指数等指标.

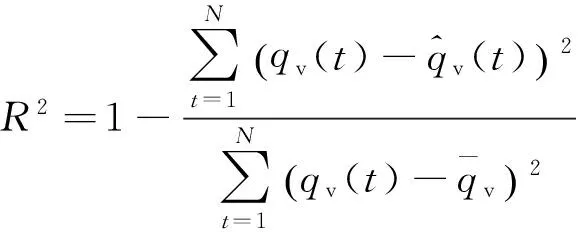
(12)

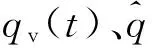
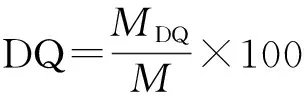
(13)

式中：MDQ为洪峰流量预报值和实测值相对误差小于等于20%的洪水场次,M为洪水总场次.

3)均方根误差(RMSE)

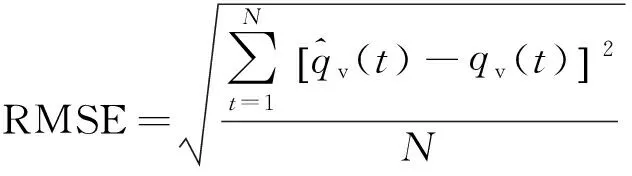
(14)

对于评估数值较大的观测值时,RMSE值能显著体现模型的优劣.RMSE值越小模式准确性越高.

(4)Gbench指数

(15)

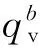
(5)相关性系数(CC)

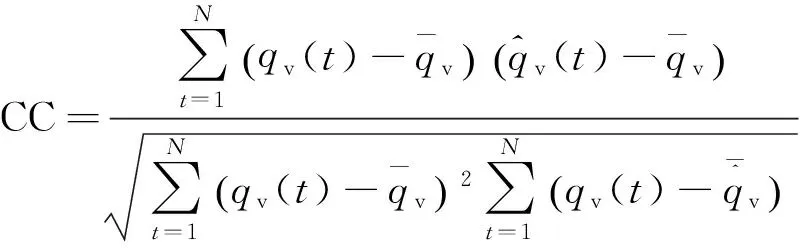
(16)

3 应 用

3.1 单一BP神经网络

图1 龙泉溪流域水系图Fig.1 Longquan river diagram

本文以浙江省境内龙泉溪流域(龙渊镇以上区域)为研究区域,如图1所示.龙泉溪是瓯江的源头,龙泉水文站控制流域面积1 440 km2.龙泉市雨量充沛,流域内多年平均降雨量1 807.8 mm.但时间分布不均,年最大降雨量为2 552.4 mm,最小降雨量为999.0 mm.雨季为4～6月,水位连续起伏,保持较高水位.龙泉溪龙渊镇以上流域,坡降6.32‰～0.97‰,河床宽为40～150 m,源短流急,水位变化快,洪峰持续时间短.降雨分布不均和地形地势特征,使得龙泉溪成为洪水多发区.本文拟构建龙泉水文站实时流量预报模型,提前1～3 h预报龙泉站流量.研究所采用的数据主要是1994～2003年龙泉溪流域发生的37场洪水要素摘录,包括龙泉站的逐时流量,以及南溪口站、山溪口站与石玄湖站逐时雨量.假定qv为龙泉站逐时流量,相关性分析筛选后初步得到qv(t)、qv(t-1)、qv(t-2)及面平均雨量这5个可能输入变量,分别标记为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ.如表1所示为不同输入组合对应得到不同的模型效果.

表1 集合神经网络模型输入变量的组合

综合考虑模型表现及模型结构复杂程度,选定输入为龙泉站qv(t-2)、qv(t-1)、qv(t)和龙泉溪流域的面平均雨量,因降水汇流时间为2～4 h,故可选定输出分别为龙泉站qv(t+1)、qv(t+2)、qv(t+3),构建3个流量预报模型.从1994～2003年的37场洪水挑选出19场洪水(5 186笔数据)作为训练样本,8场洪水(1 769笔数据)作为验证样本,10场洪水(1 749笔数据)作为测试样本.神经网络模式采用目前使用最广泛的倒传递神经网络(BPNN).隐层层数为一层,试错法率定隐层神经元个数为4个,网络结构为4-4-1,从而构建预见期为1-3h的实时流量预报模型.采用matlab中newff函数构建BP模型,训练算法为trainlm.

3.2 集合BP神经网络

集合神经网络包括产生集合成员和整合集合成员2大步骤.本研究使用初始值扰动、bagging重采样及boosting重采样3种产生方式,再利用简单平均和贝叶斯模型加权平均对成员进行整合,共6种集合预报组合.而研究也表明,当集合成员数量为20个时,能够获得显著效果[19],因此本研究所建立的6种预报组合,皆产生20组集合成员,作为评估与比较的标准.

1)ENN_1(ensemble neural network) 通过随机改变初始权值来产生集合成员,再使用简单平均整合集合预报.

2)ENN_2 通过随机改变初始权值产生集合成员,再使用BMA整合集合预报.

3)ENN_3 利用bagging算法对原始训练数据组重采样产生20次不同的训练数据组训练神经网络,再使用简单平均整合集合预报.

4)ENN_4 利用bagging算法对原始训练数据组重采样产生20次不同的训练数据组训练神经网络,再使用BMA整合集合预报.

5)ENN_5 利用boosting算法对原始训练数据组重采样产生20次不同的训练数据组训练神经网络,再使用简单平均整合集合预报.

6)ENN_6 利用boosting算法对原始训练数据组重采样产生20次不同的训练数据组训练神经网络,再使用BMA整合集合预报.

4 结果对比分析

运行单一BP网络(SNN),使用训练集不断调整网络参数至最佳(学习率为0.1,训练步数为200步,训练目标为10-6),保存网络模型.利用验证集检查神经网络模型是否存在“过拟合”.若不存在“过拟合”,输入测试集进行网络仿真,输出最佳单一神经网络流量预报值.使用不同集合策略产生6种集合预报组合,并输出集合神经网络流量预报.特别说明,为保证模式的可对比性,集合神经网络的网络参数(包括训练步数、学习率、训练目标等)与单一神经网络的参数相同.如表2、3、4中分别为6种集合神经网络模型与单一神经网络模型应用于龙泉站不同预见期tf下流量预报的确定性系数、均方根误差值、Gbench指数.对比这3个指标可以发现,单一神经网络模型的表现明显差于集合神经网络模型.从表3中发现,相较于单一神经网络,集合神经网络模型的性能可提高15%～35%.预见期越长,提高程度越低.

此外,从表2、3、4中亦可发现,6种集合神经网络组合,最差的是ENN_5组合.原因可能是考虑到模型运行时间较长,加权平均误差(式(4)计算所得)取值略大,使得迭代不够充分,重采样得到的样本质量没有足够好.但是ENN_6组合表现仍令人满意,凸显了贝叶斯模型加权平均的优势.从Gbench指数中,对比ENN_1和ENN_2、ENN_3和ENN_4,BMA整合的6组集合预报中4组优于简单平均,其余2组效果与简单平均接近.因此,BMA整合方法整体优于简单平均.此外,可从表中得到,对初始值细微扰动(ENN_1/ENN_2),产生多组不同的初始参数进行多次重复的计算并从中抽取有用信息,操作简单且能收到不错的效果,也说明了该方法是目前最热门的集合技术的原因.从3个指标分析,boosting重采样技术应用于集合神经网络的表现稍好于bagging重采样技术,最好的模型是由boosting算法和BMA组合的集合神经网络模型(ENN_6).

洪水预报一直是水文预报的热点和趋势,洪峰流量值和峰现时间是评估洪水预报模型优劣的2大指标.如表5所示为洪峰流量值预报合格率.从表5中可以发现,洪峰合格率随预见期的增加而降低.集合神经网络模型的表现优于单一神经网络模型,特别是长预见期的洪峰预报.从洪峰合格率指标中发现,重采样对应的集合预报组合的洪峰合格率基本达100%,重采样技术优于初始值扰动方法.

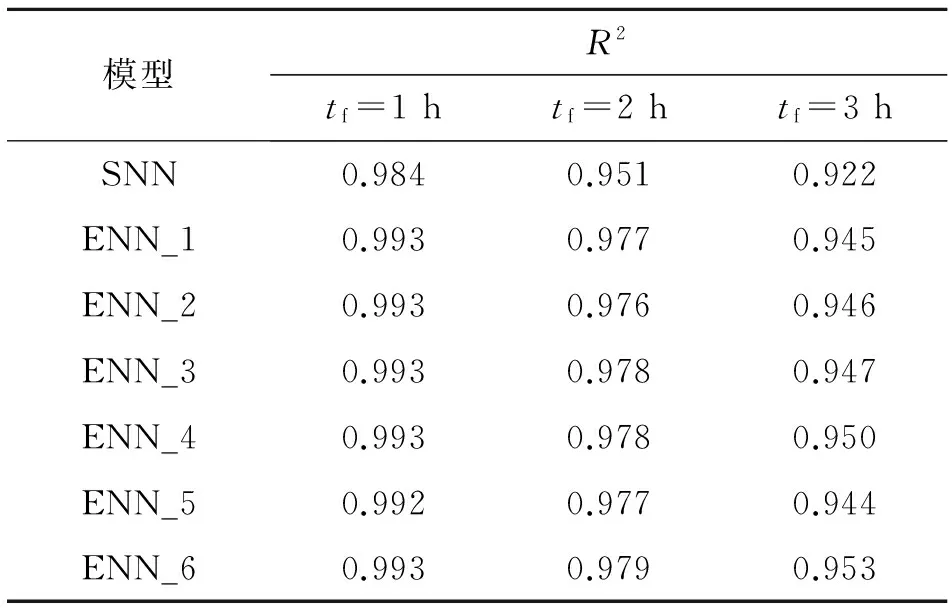
表2 神经网络模型的确定性系数

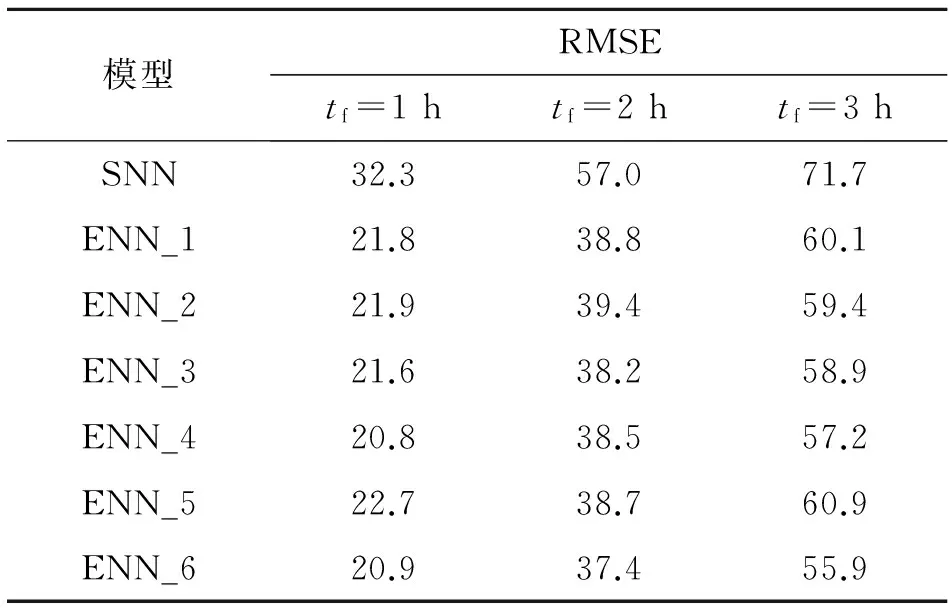
表3 神经网络模型的均方根误差

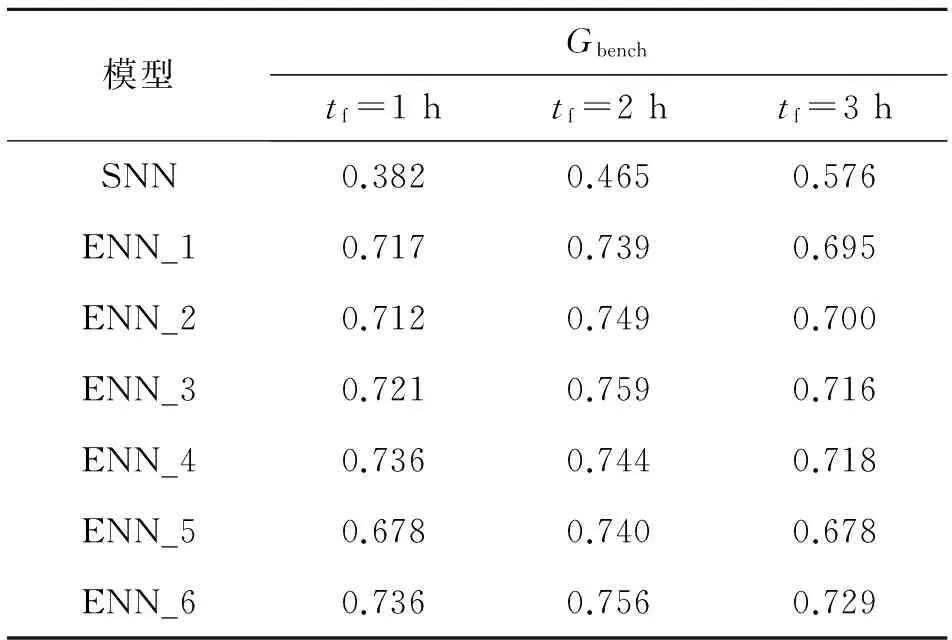
表4 神经网络模型的Gbench指数

表5 神经网络模型的洪峰合格率

如图4所示为基于集合神经网络模型(ENN_6)、测试阶段最大洪峰对应预见期tf为1～3 h预报结果.可以从图4中发现,由20个集合成员组成的集合预报区间,基本覆盖实测流量过程线.由此可见,集合预报的优势在于,一是经整合后的预测值比单一神经网络的预测值更接近于实测值,二是可提供覆盖实测流量过程线的预报区间.这在流量极值预报上的意义重大.此外,从图4可发现,预见期越长,预测精度变低,预报区间带宽变大.实际作业预报中,使用boosting算法与贝叶斯模型加权平均的组合构建集合神经网络模型.利用贝叶斯模型加权平均得到单一均值预报,作为常规的预报；辅于集合预报区间的上限考虑洪水可能极值,用于指导防范工作.

图2 基于神经网络的流量预报趋势图Fig.2 Streamflow forecast based on neural network

图3 基于神经网络的流量预报散点图Fig.3 Streamflow forecast scatterplot based on neural network

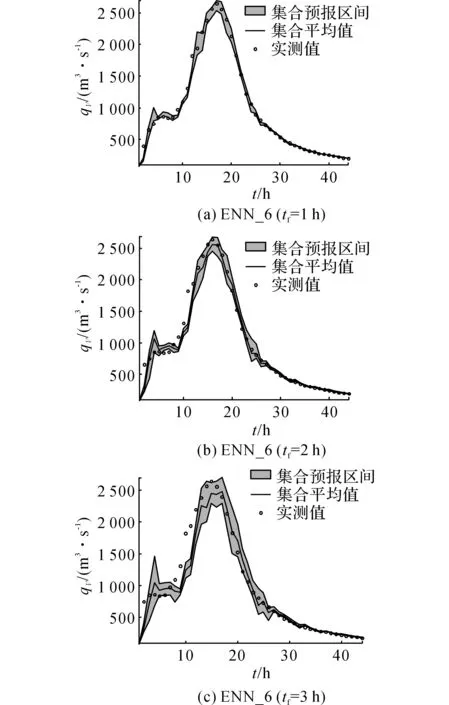
图4 基于集合神经网络的洪峰流量预报Fig.4 Peak Flood forecast based on ensemble neural network

5 结 论

人工神经网络模型的不确定性来源包括自变量选取的不确定性、模型的不确定性(主要来自模式、初始值及参数等)、数据的不确定性(主要指数据本身存在偶然性误差和系统性误差).本研究将集合概念导入人工神经网络模型,综合考虑模型及数据的不确定性,构建集合神经网络模型.模型以龙泉站前3个小时的流量和龙泉溪流域面平均雨量为输入,对龙泉水文站进行预见期为1～3 h的流量预报.可得到如下4个结论：

(1)相较于单一神经网络模型,集合神经网络模型可显著提高流量预报的效果,特别是使用boosting算法与BMA策略的组合.在进行长预见期的流量预报,集合神经网络依旧存在优势.本研究表明,集合预报概念亦适合应用于水文预报,并且能取得较好的效果.

(2)对初始值细微扰动的集合策略不仅操作简单,而且由此构建的集合神经网络模型效果亦佳.在本研究中,由重采样策略产生的集合神经网络模型效果稍好于初始值策略,但是重采样策略操作复杂度较大且由其构建的模型实际运行时间要长于初始值策略.这说明,初始值策略是一种简单、易行且高效的集合策略.

(3)利用重采样技术构建集合神经网络模型,boosting算法的效果要略好于bagging算法,特别是长预见期的预报.但boosting算法要花费足够多的时间来加强训练那些拟合较差的样本,模型实际运行时间也长于bagging算法.

(4)BMA的整合效果要略优于简单平均.从原理上,BMA赋予较优模型更大的权重,整合得到的效果应该要比简单平均的整合效果好,但实际效果不显著.

[1] 俞亭超,张土乔,毛根海,等.预测城市用水量的人工神经网络模型研究[J].浙江大学学报:工学版,2004,38(9): 1156-1161．

YU Ting-chao,ZHANG Tu-qiao,MAO Gen-hai, et al. Study of artificial neural network model for forecasting urban water demand [J]. Journal of Zhejiang University: Engineering Science, 2004, 38(9): 1156-1161．

[2] 隋彩虹,徐宗学.人工神经网络模型在渭河下游洪水预报中的应用[J].水文,2006,26(2): 38-42．

SUI Cai-hong,XU Zong-xue. Application of ANN models in flood forecasting for the lower reach of the Weihe river [J].Journal of China Hydrology,2006,26 (2): 38-42．

[ 3 ] CHIANG Y M, CHANG L C, CHANG F J. Comparison of static-feedforward and dynamic-feedback neural networks for rainfall-runoff modeling [J]. Journal of Hydrology, 2004, 290(3): 297-311．

[4] 徐伟,董增川,付晓花,等.基于BP人工神经网络的河流生态健康预警[J].河海大学学报:自然科学版,2015,43(1): 54-59．

XU Wei,DONG Zeng-chuan,FU Xiao-hua, et al． Early warning of river ecosystem health based on BP artificial neural networks [J].Journal of Hohai University ：Natural Sciences, 2015, 43(1): 54-59．

[5] 胡健伟,周玉良,金菊良.BP神经网络洪水预报模型在洪水预报系统中的应用[J].水文,2015,35(1): 20-25．

HU Jian-wei, ZHOU Yu-liang, JIN Ju-liang. Flood forecasting model on BP networks and its application in flood forecasting systems [J].Journal of China Hydrology, 2004, 290(3): 297-311．

[6] 吕庆平,罗坚,朱坤,等.基于人工神经网络的热带气旋路径预报试验[J].广东气象,2008,31(1): 15-18．

LU Qing-ping, LUO Jian, ZHU Kun, et al. Experiments on predicting tracks of tropical cyclones based on artificial neural network [J]. Guangdong Meteorology, 2008, 31(1): 15-18．

[7] 孙军波,钱燕珍,陈佩燕,等.登陆台风站点大风预报的人工神经网络方法[J].气象,2010, 36(9): 81-86．

SUN Jun-bo,QIAN Yan-zhen,CHEN Pei-yan, et al. The artificial neural network method on the station wind in landfall typhoon [J]. Meteorological Monthly, 2010, 39(9): 81-86.

[8] 包红军,赵琳娜.基于集合预报的淮河流域洪水预报研究[J].水利学报,2012,43(2): 216-224.

BAO Hong-jun,ZHAO Lin-na. Flood forecast of Huaihe river based on TIGGE ensemble predictions [J].Journal of Hydraulic Engineering, 2012, 43(2): 216-224．

[9] 孙照渤,谭桂容,赵振国,等.中国东部夏季雨型的人工神经网络集合预测[J].大气科学学报,2013,36(1): 1-6.

SUN Zhao-bo,TAN Gui-rong,ZHAO Zhen-guo, et al. Ensemble prediction of summer rainfall patterns over eastern China based on artificial neural networks [J].Journal of Nanjing Institute of Meteorology, 2013, 36(1): 1-6．

[10] KASIVISWANATHAN K S, CIBIN R, SUDHEER K P, et al. Constructing prediction interval for artificial neural network rainfall runoff models based on ensemble simulations [J]. Journal of Hydrology, 2013, 499: 275-288．

[ 11 ] El-SHAFIE A, NAJAH A, ALSULAMI H M, et al. Optimized neural network prediction model for potential evapotranspiration utilizing ensemble procedure [J]. Water Resources Management, 2014, 28(4): 947-967．

[12] ZAIER I, SHU C, OUARDA T B M J, et al. Estimation of ice thickness on lakes using artificial neural network ensembles [J]. Journal of Hydrology, 2010, 383(3): 330-340.

[13] OUARDA T B M J, SHU C. Regional low-flow frequency analysis using single and ensemble artificial neural networks [J]. Water Resources Research, 2009, 45(11): 114-122．

[14] ARAGHINEJAD S, AZMI M, KHOLGHI M. Application of artificial neural network ensembles in probabilistic hydrological forecasting [J]. Journal of Hydrology, 2011, 407(1-4): 94-104．

[15] MONMOUTH H, HARRIS DRUCKER. Improving regressors using boosting techniques [C]∥ Proceedings of the Fourteenth International Conference on Machine Learning. San Francisco: Morgan Kaufmann Publishers Inc. 1997: 107-115．

[16] 杜新忠,李叙勇,王慧亮,等.基于贝叶斯模型平均的径流模拟及不确定性分析[J].水文,2014,34(3): 6-10.

DU Xin-zhong,LI Xu-yong,WANG Hui-liang, et al. Multi-model Ensemble runoff simulation based on bayesian model averaging method and model structure uncertainty analysis [J].Journal of China Hydrology, 2014, 34(3): 6-10．

[17] 董磊华,熊立华,万民.基于贝叶斯模型加权平均方法的水文模型不确定性分析[J].水利学报,2011,42(9): 1065-1074．

DONG Lei-hua,XIONG Li-hua,WAN Min．Uncertainty analysis of hydrological modeling using the Bayes Model Averaging Method [J].Journal of Hydraulic Engineering,2011, 42(9): 1065-1074.

[18] SEIBERT J. On the need for benchmarks in hydrological modeling [J]. Hydrological Processes, 2001, 15(6): 1063-1064．

[19] HERR H D, KRYSZTOFOWICZ R. Bayesian ensemble forecast of river stages and ensemble size requirements [J]. Journal of Hydrology, 2010, 387(13):151-164．

Flood forecasting by ensemble neural networks

CHIANG Yen-ming1, ZHANG Jian-quan1, MING Yan2

(1.InstituteofHydrologyandWaterResourcesEngineering,ZhejiangUniversity,Hangzhou310058,China；2.DepartmentofArchitecture,ZhejiangUniversity,Hangzhou310058,China)

Regarding the flood prevention, the concept of ensemble prediction was integrated into artificial neural networks by considering the data quality and initial weights to reduce the uncertainties of single neural network. The ensemble neural networks were built for 1～3 h ahead flood forecasting in Longquan River Basin, by generating the ensemble members through resampling and initialization methods and combining the model outputs through the arithmetic average and Bayesian model average (BMA). Results indicate that the ensemble neural networks significantly improve the flood forecasting accuracy as compared with the single neural network. The accuracy of ensemble neural network is about 15% to 35% higher than that of the single neural network in terms of root mean square error. Among various ensemble strategies, the combination of initialization and arithmetic average has simpler structure and less computational time; the improvement percentage rangs from 16% to 32%. The forecasts accuracy obtained from the combination of boosting and BMA are improved 22% to 35%.

flood forecasting; artificial neural network (ANN); Bayesian model average (BMA); ensemble prediction

2015-12-10.

教育部博士点新教师资助项目(J20131413)；浙江省教育厅一般资助项目(N20130036).

江衍铭(1978—),男,副教授,从事水文水资源等研究.ORCID: 0000-0002-6303-9303. E_mail: chiangym@zju.edu.cn

明焱,男,副教授.ORCID: 0000-0002-6889-9580,mmmgmmm@vip.sina.com

10.3785/j.issn.1008-973X.2016.08.007

TV 213

A

1008-973X(2016)08-1471-08

浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng