基于小波分析气门落座数据处理方法的研究

李亚东 ,梁　奇

（杭州电子科技大学机械工程学院,杭州 310018）

基于小波分析气门落座数据处理方法的研究

李亚东 ,梁奇

（杭州电子科技大学机械工程学院,杭州 310018）

本文主要提供了一种快速傅里叶变换（FFT）分析同小波包分析相联合的数据处理方法。通过对处理后的加速度积分后所获得的气门速度数据信号，分析计算可得其干扰信号在数字滤波的基础上减少了11.84%，气门落座速度的精度也相对提升了15%，绝对误差为6.59%。跟传统的数字滤波器滤波的方式对比，此种方法有效提升了气门落座动态数据的精度。

数字滤波器；快速傅里叶变换；小波包分析；气门落座

0 　引言

本文主要针对使用常见的数字滤波器滤波方法在处理气门落座动态数据时的缺陷，提出将快速傅里叶变换（FFT）分析与小波包分析相结合的数据处理方法，实现信号和误差的滤波，有效地提高了数据的精度。

1　数字滤波器滤波分析气门落座动态数据

气门的动态数据在时域和频域内的区分不是很明显，在时域内，干扰信号总是存在；在频域中，其信号不仅包含有与凸轮转速同步的周期信号以外，还隐藏了气门开启和落座时的冲击信号。而冲击信号不是严格的周期信号，其在频域和干扰噪声有部分的重叠[1]。

本文采用高通滤波器，设置其低频、高频阻带值为8Hz、10KHz，对气门加速度信号做滤波处理。由结果分析可知，经过数字滤波处理后其最大值由原始信号的10049m/s2变为了9782m/s2，产生了2.65%的滤波误差，其落座端的动态数据态势也与原始信号在时间上有一定程度上的偏差。由此可见，滤波器在去除干扰信号的同时，真实信号也被削弱了，尤其是气门落座段部分的高频信号被削弱了。

2　小波分析气门动态数据处理的拓展研究

小波变换具备多频率分析信号的特征，是一种信号的时间-频率分析方法，并且在时域、频域内均具有表征信号局部特征的功能。根据这个特点，将气门落座的单个周期的动态数据分为工作段（A’-B）、落座段（B-C）、非工作段（A-A’和C-C’），如图1所示。

图1　气门加速度曲线分段图

2.1 FFT分析与小波包分析相结合去除干扰

小波包分析是由小波分析拓展而来，能够对信号做更细致的分析和重构，可以同时对低频信号和高频信号做出分解，并在全局频段内对信号做细化，所以，用该方法可以去除夹杂在气门加速度动态数据中的干扰[2]。对预处理后的气门加速度数据各工作段进行FFT分析。整个频域段均包含着落座段部分的真实信号，而干扰信号则主要存在于加速度曲线各段FFT变换后图形的突变处和曲线的粗糙部分。结合上述分析可获得干扰信号频率范围分别是：0-3阶、145-148阶、380-394阶和438-442阶。为了进一步去除干扰，必须对原始加速度数据信号进行442阶以上的细分，即需要对其做9层小波包分解，其512阶频率信号则被分成了512个频率段。再通过小波包对上述干扰频率范围进行重构从而消除干扰。

2.2 对比分析

经过上述分解与重构，将常用数字滤波器去除干扰与小波包去除干扰所得的结果进行对比，效果如图2所示。

图2　常用数字滤波处理和小波处理后加速度曲线对比

对图2中数字滤波去除干扰和小波包去除干扰的的气门加速度曲线进行积分获得气门速度曲线，其对比图如图3所示。

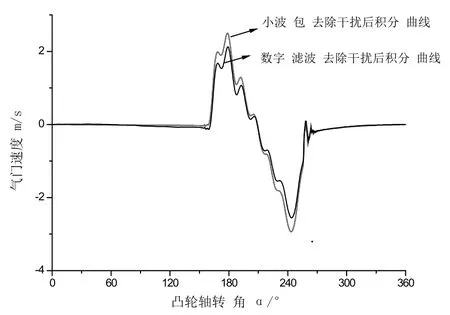
图3　处理后加速度曲线积分所得速度曲线对比

根据图3的显示分析可知，小波包处理和数字滤波处理后的速度信号，其最大值前者为2.936m/s，后者为2.555m/s，原始数据所得为3.142m/s。采用FFT分析与小波包分析相结合的方式处理气门落座数据，通过对其积分后获得的气门速度信号，计算可得其干扰信号在数字滤波的基础上减少了11.84%，气门落座速度的精度也相对提升了15%，绝对误差为6.59%。

3　结论

采用FFT分析与小波包分析相结合的方法去除干扰后，气门的加速度曲线和积分后得到的气门速度曲线的最大值不变，其真实性未受到影响，改善了数字滤波容易丢失真实信号的缺陷，有效的提高了配气机构动态数据的精度。

[1]谢勇.发动机四气门配气机构系统分析研宄[D].上海交通大学硕士学位论文,2009.

[2] 何庆飞.基于奇异值分解和小波包分析的液压泵振动信号特征提取方法[J].数据采集与处理,2012(02):241-247.

10.16640/j.cnki.37-1222/t.2016.21.208