“囚徒困境”在贿赂犯罪审讯中的运用
尹立栋
内容摘要:博弈分析可用于职务犯罪侦查的审讯过程,其中囚徒困境模型对于分化贿赂犯罪中的受贿人与行贿人联盟具有重要价值。可以根据贿赂案件本身的特点,将囚徒困境模型应有于审讯职务犯罪嫌疑人,促使犯罪嫌疑人如实自愿供述。
关键词:职务犯罪侦查 囚徒困境 讯问 博弈论
一、囚徒困境模型的核心内容
囚徒困境是博弈论中的典型模型,其最初理论形态由梅里尔·弗拉德和梅尔文·德雷希尔提出,后由阿尔伯克·塔克以两个囚徒故事的方式予以阐述,并命名为“囚徒困境”。塔克设置的囚徒困境如下:警察在盗窃现场附近抓住了两名携带武器的嫌疑犯阿尔和鲍勃,将他们分别隔离审讯,并分别向他们开出了可以释放的条件——供述其犯罪行为。在这样一种困境中,两人的策略选择只有招供或者不招供。如果两个人都不招供,警方由于没有掌握他们盗窃的证据,只能以非法携带武器这一较轻的罪名提出指控,最终两名嫌疑犯各将被判处一年监禁。如果两个人都选择招供并指控对方,由于认罪态度较好,两人都将被判处十年监禁。如果其中有一人招供并指认对方,而对方仍然选择不招供,那么招供的人将被免于起诉,对方将被判处二十年监禁。
囚徒困境的基本博弈结构,可以用如下收益矩阵表格表示:
囚徒困境中,两名囚徒选择的都是对自己最有利的策略,恰恰得到的是一个较差的结果。这就是“困境”所在,也正是囚徒困境原理的精髓所在。这种结果取决于以下三个条件。
第一,规则设置的合理性。囚徒困境中,囚徒们选择不同策略,将导致巨大的收益差异。囚徒只要招供,就可以避免可怕的20年监禁。即使对方招供,自己也只获刑10年,甚至可能由于对方不招供而获得释放。这种规则设置能够有效排除囚徒之间的合作。
第二,理性人假设。博弈论分析有效的前提之一是理性人假设,即人都是理性的,博弈方都以获取个体利益最大化为追求目标,且有准确的判断选择能力,也不会“犯错”。虽然理性又有个体理性和集体理性之别,且现实中的博弈参与人都有可能犯错误,但是从警察的角度看,利用囚徒困境时应当最大限度地强化囚徒的个体理性而弱化其集体理性,并尽量减少囚徒在策略选择时的犯错几率。
第三,信息阻断的作用。囚徒困境中,将两名囚徒隔离审讯至关重要。隔离审讯造成两名囚徒之间的信息阻断,“离间”了囚徒们的信任关系,从而促使他们从利己的理性角度出发,作出招供的策略选择。
二、囚徒困境在贿赂犯罪审讯中的演绎
(一)囚徒困境在贿赂犯罪审讯中的情形设置
第一,共同受贿嫌疑人之间的囚徒困境。二个或二个以上的受贿人共同收受行贿人的财物,属于共同犯罪的范畴,是最典型的囚徒困境。第二,行受贿对合犯之间形成的囚徒困境。虽然不同于共同犯罪,但具有共同犯罪的某些共性特征,双方都必须依据对方的行为才能完成自己的犯罪行为,且对对方的犯罪行为都十分清楚,只要条件设置合理,在审讯中就能形成囚徒困境。第三,同一案件行贿人之间形成的囚徒困境。根据受贿人多头受贿的犯罪特点,实践中侦查部门往往会对指向同一受贿人的二名或二名以上行贿人进行先期同时审讯。虽然行贿人之间并没有犯罪行为的牵连,也不知道其他行贿人实施犯罪行为的真相,但是他们的共同特点在于向同一受贿人实施行贿行为。基于此一显著特点,侦查部门可以给他们设置如下规则:先交代行贿事实,认罪态度较好的予以释放;拒不交代行贿事实,态度恶劣的则予以刑事拘留,甚至追究刑事责任。据此将他们设定于囚徒困境之中,这也是实践中屡试不爽的审讯策略之一。第四,窝串案中形成的混合型囚徒困境。在查处窝串案,尤其是在侦查一体化机制运作的过程中,经常会出现对多名行贿人和多名受贿人进行同时审讯的场境。在此条件下,审讯人员可以对行贿人设置上述同样规则:即先行交代行贿事实,认罪态度较好的予以释放;拒不交代行贿事实,态度恶劣的则予以刑事拘留,甚至追究刑事责任。而对于同时受审的受贿人则可以如此设置规则:先交代受贿事实,且认罪态度较好的,可以得到从轻或减轻处罚,况且还可能存在检举揭发他人犯罪事实、争取立功减刑的有利条件;不交代受贿事实,且认罪态度不好的,将面临从重处罚的后果。据此将他们全部推入囚徒困境之中,实现分化瓦解,争取优先交代的优势策略。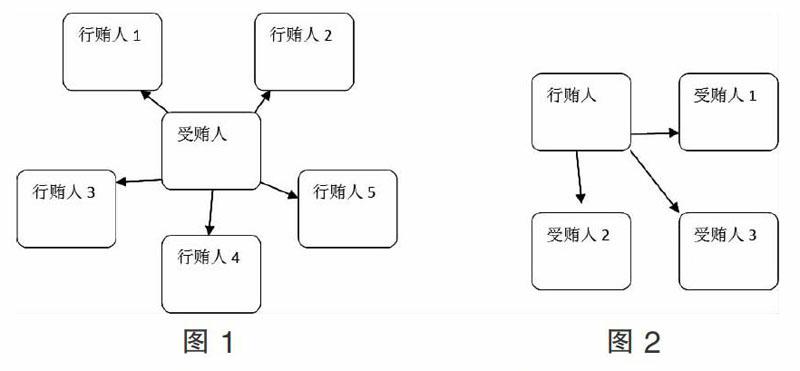
(二)贿赂犯罪中多重囚徒困境的模型构建
受贿人多头受贿和行贿人多向行贿的现实特点为构建贿赂犯罪审讯的多重囚徒困境搭建了平台。如图1和图2所示:
在图1中,假设针对受贿人A存在着多个行贿人。从理论上讲,受贿人A在接受审讯时,将面临行贿人1、行贿人2、行贿人3……等多个囚徒困境,而不仅仅是一个囚徒困境。如前所述,受贿人A在针对一个行贿人的囚徒困境中,其优势策略的选择是背叛,那么在针对多个囚徒困境中,其优势策略的唯一选择只能是背叛,从而作出交代受贿事实的选择。但是,实践中受贿人A事实上会对哪个或哪几个行贿人作出背叛,关键还在于完全信息的获取。受贿人A会通过审讯中所获取的信息对可能暴露的行贿人和行受贿事实进行猜测,以期决定背叛谁或者隐藏谁。客观上,审讯人员只能掌握其中1-2个或者少数行贿人。在此局面下,侦查人员的策略就是藏好底牌,营造信息不对称,迫使受贿人A背叛更多的行贿人。
同理,在图2中,我们假设行贿人1向受贿人A、受贿人B、受贿人C三个人行贿,而审讯人员仅掌握了受贿人A的信息。那么在审讯行贿人1时,就应当营造已经完全掌握行贿人1全部行贿信息的假象,使其坠入三个囚徒困境之中做出选择。无论行贿人1是否首先交代向受贿人A的行贿事实,只要其选择对受贿人B的背叛就是小胜,再选择对受贿人C的背叛就是大胜,而对受贿人A的背叛只要审讯人员适时地泄露信息即可,据此就能取得审讯工作的全胜结局。
为了进一步理解贿赂犯罪审讯中的多重囚徒困境,我们再从以下两个层面进行阐述。
第一,行贿人之间的多重囚徒困境构建。设置多个囚徒困境更有利于突破案件。如果初查工作足够仔细,从中发现了多名行贿人,就可以设置多重囚徒困境,推进审讯工作的快速发展。假设在侦查力量充足的前提下,侦查部门同时传唤四名行贿人且同时对其进行审讯,就会形成如图局势。
在图3中,假设给四名行贿人设定同样的规则:交代就释放,不交代则予以刑拘。就单个囚徒困境而言,如行贿人与行贿人之间形成囚徒困境,双方的优势策略仍然是选择交代而获得释放。何况在四个行贿人之间形成的囚徒困境中,每个行贿人都面临三个囚徒困境,同时还要受到其他行贿人之间的多个囚徒困境的威胁。任何一个行贿人的优势策略只能是,而且也必须是如实交代。如果作出不交代的选择,将面临被刑拘的严重后果。
图中还设置了“?”的格式,也就是说在共同不交代的情况下应当如何处置呢?其实答案不言自明,只能是刑拘,即“?”=“刑拘”。因为只要有1个行贿人选择交代,那么其他人即使不交代均要承担100%的被背叛、被刑拘的风险。况且,如果个别行贿人都选择了暂时不交代行贿行为的策略,被刑拘后仍然摆脱不了囚徒困境的困扰,在稍后完全信息明了之时,如受贿人交代了其行贿事实之后,该行贿人的策略选择仍旧是交代犯罪事实。由此,该图情形进一步说明了同时传唤多名行贿人的优势策略所在。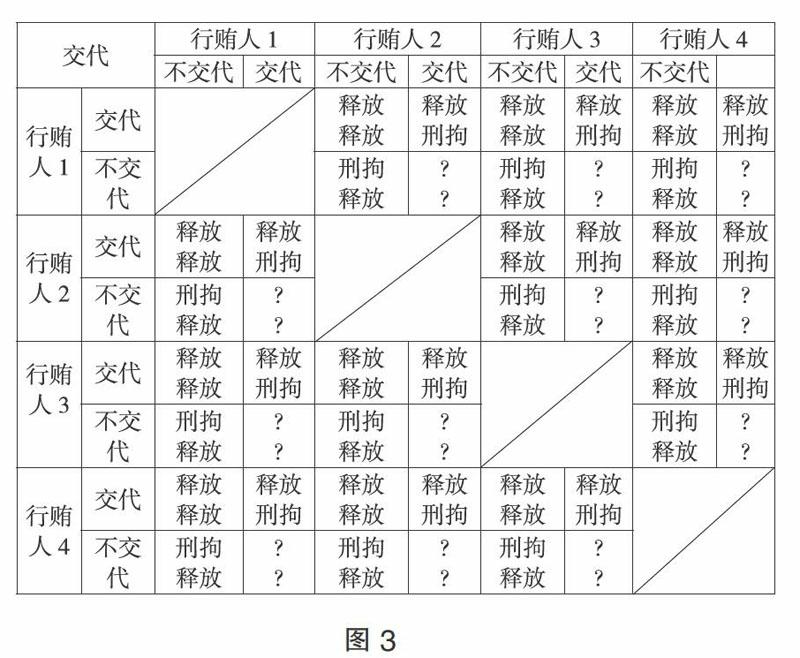
第二,嵌入受贿人之后的多重囚徒困境设计。图3描述行贿人之间的博弈情形。实践中,一般都在2名左右的行贿人交代的情况下,适时传唤受贿人。这将形成下图的囚徒困境模型。
如图4所示,假设行贿人1和行贿人2已作交代,且行贿数额之和已经超过10万元,那么受贿人将面临10-15年有期徒刑,如果受贿人交代,将得到接近于10年的从轻处罚,如果其不交代则面临接近于15年的从重处罚。如果侦查机关在传唤受贿人的同时,再传唤行贿人3和行贿人4,此时对于行贿人3和行贿人4而言,他们是否交代已经无关案件定性和量刑,其优势策略只能是尽快作出交代的抉择。因为不交代,可能还将受到5年有期徒刑的惩罚。实践中,受贿人被立案和羁押前,审讯行贿人的难度,要远远大于受贿人被羁押后审讯行贿人的难度,道理正在于此。
(三)囚徒困境在贿赂犯罪中的推演
根据贿赂犯罪多头受贿、多向行贿以及职务犯罪窝串案多发的特点和规律,我们对贿赂犯罪案发网络进行分析,并构建贿赂犯罪侦查审讯的囚徒困境博弈树。
图中所示,直线连接的人物之间可以在审讯中构成一个囚徒困境,整幅图展示的是交错重叠、纵横复杂的贿赂犯罪窝串案发关系和侦查规律网络。但它也只能反映出行业型、区域型窝串案的基本框架,实际发生的情况还要比之复杂许多。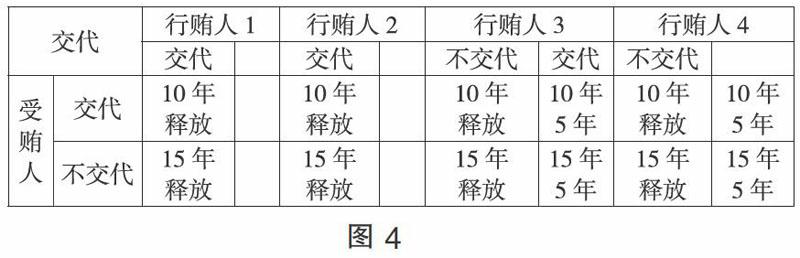
如图5所示,实践中构筑囚徒困境模型方法众多,每一条线段连接的两名对象均可以构成囚徒困境,基于内容表述的复杂性和本文篇幅限制,对此多重囚徒困境博弈模型的分析只能从略。
三、囚徒困境给贿赂犯罪审讯的启示
囚徒困境是职务犯罪侦查中的博弈总策略,在各个阶段可以设置不同的规则予以灵活运用。
第一,囚徒困境策略的运用取决于“隔离”的状态。审讯对象被传唤并接受审讯以后,就处于与外界隔绝的状态,其信息获取的唯一渠道只能是审讯人员。因此,迅速、及时地传唤审讯对象到案尤为重要,可以削弱审讯对象对自身犯罪事实信息完全掌握的优势心理。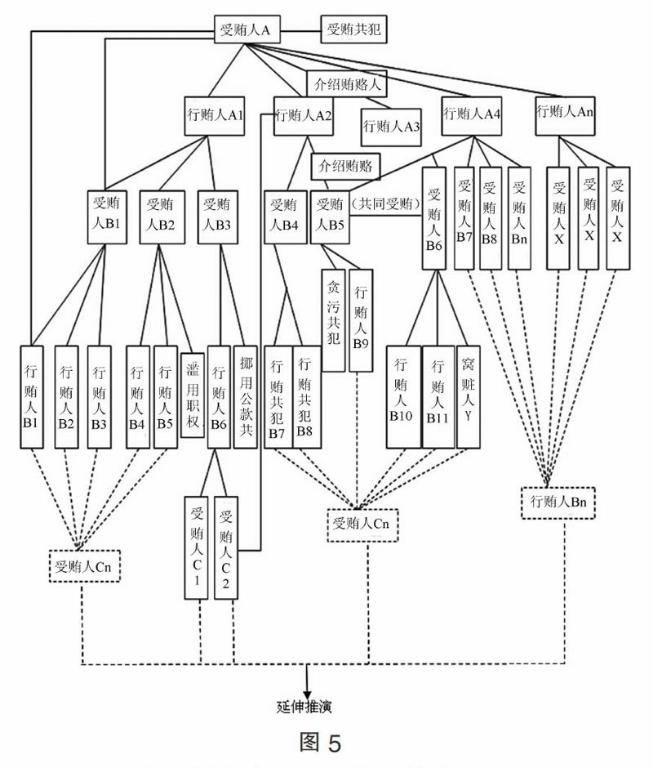
第二,囚徒困境策略的成败取决于审讯人员优势策略的驱动。审讯对象深陷囚徒困境之后,基于其趋利避害的利己理性考虑,并不会立即作出交代的策略选择,仍然会千方百计地观察审讯人员的策略行动,据此作出有利于己方的行动选择。为此审讯人员采取怎么样的策略选择仍然是驱动审讯对象供述犯罪事实的外力因素。审讯人员应当围绕审讯对象的应讯心理施以合理的博弈策略:一是坚决地让审讯对象相信审讯人员已经掌握其全部或部分犯罪事实。二是增强其对法律知识的共同认识,增强其对从轻、减轻处罚的收益期待。三是以情感触动开路,使其充分相信审讯人员的理性,最终促使其尽快交代。

