MapReduce based computation of the diffusion method in recommender systems①
Peng Fei (彭 飞):You Jiali:Zeng Xuewen:Deng Haojiang
(*National Network New Media Engineering Research Center:Institute of Acoustics,Chinese Academy of Sciences:Beijing 100190:P.R.China)(**University of Chinese Academy of Sciences:Beijing 100049:P.R.China)
MapReduce based computation of the diffusion method in recommender systems①
Peng Fei (彭 飞)*To whom correspondence should be addressed.E-mail:pengf@dsp.ac.cnReceived on July 26,2015***:You Jiali*:Zeng Xuewen*:Deng Haojiang*
(*National Network New Media Engineering Research Center:Institute of Acoustics,Chinese Academy of Sciences:Beijing 100190:P.R.China)(**University of Chinese Academy of Sciences:Beijing 100049:P.R.China)
The performance of existing diffusion-based algorithms in recommender systems is still limited by the processing ability of a single computer.In order to conduct the diffusion computation on large data sets:a parallel implementation of the classic diffusion method on the MapReduce framework is proposed.At first:the diffusion computation is transformed from a summation format to a cascade matrix multiplication format:and then:a parallel matrix multiplication algorithm based on dynamic vector is proposed to reduce the CPU and I/O cost on the MapReduce framework:which can also be applied to other parallel matrix multiplication scenarios.Then:block partitioning is used to further improve the performance:while the order of matrix multiplication is also taken into consideration.Experiments on different kinds of data sets have verified the efficiency of the proposed method.
MapReduce:recommender system:diffusion:parallel:matrix multiplication
0 Introduction
Recommender systems[1]adopt knowledge discovery techniques to provide personalized recommendations.It is now considered to be the most promising way to efficiently filter out the overload information.Thus far:recommender systems have successfully found applications in e-commerce:such as book recommendations in Amazon.com[2]:movie recommendations in Netflix.com[3]:and so on.
Collaborative filtering (CF) is currently the most successful technique in the design of recommender systems[4]:where a user will be recommended with items that people with similar tastes liked in the past.As the CF technique evolves:some diffusion-based algorithms were proposed for better prediction accuracy.Huang et al.[5]proposed a CF algorithm based on an iterative diffusion process.Considering the system as a user-item bipartite network:Zhou:et al.[6]proposed an algorithm based on two-step diffusion.Zhang:et al.[7]proposed an iterative opinion diffusion algorithm to predict ratings in Netflix.com.
As the size of data grows rapidly:many researchers have focused on the design of distributed recommender algorithms.Jiang:et al.[8]and Zhao:et al.[9]proposed an item-based CF algorithm and a user-based CF algorithm based on Hadoop[10]respectively.Sebanstian et al.[11]proposed a KNN algorithm based on user similarity and implemented it on the MapReduce framework[12].However:there is little research on diffusion-based recommender algorithms on the MapReduce framework.
As the diffusion-based recommender methods are based on graphs:matrix multiplication can be used to perform the computation task:which can facilitate parallel processing as shown in the next sections.Li:et al.[13]used a parallel matrix multiplication method to do the similarity calculation in recommender systems.They proposed a single tuple method (STM) and a row divided method (RDM) to implement the matrix multiplication computation on the MapReduce framework.STM is rather inefficient as will be explained in the following sections.RDM requires servers in the Hadoop cluster to save the whole matrix in memory:which cannot be used on large data sets.Zheng:et al.[14]proposed a parallel matrix multiplication algorithm based on vector linear combination.However:it still needs servers to save the whole matrix in memory in the reduce step:which suffers from the same problem with RDM.
In order to make the diffusion-based recommender methods applicable on large data sets:a parallel cascade matrix multiplication algorithm is proposed to realize the classic diffusion method[6]on the MapReduce framework.The contributions of this work are as follows:
(1) The classic diffusion method in recommender systems is transformed from the summation format to the cascade matrix multiplication format:which can facilitate parallel processing.
(2) A parallel matrix multiplication algorithm based on dynamic vector on the MapReduce framework is proposed:which can reduce the CPU and I/O cost effectively.In addition:the algorithm is improved by block partitioning.The order of matrix multiplication is also taken into consideration to enhance performance.
(3) Experiments are conducted on different kinds of data sets:including MovieLens and Jester:to verify the effectiveness of the proposed method.
The rest of this paper is organized as follows.Section 1 gives the background information of the study.Section 2 introduces the vectorization of the classic diffusion method and describes our dynamic vector based matrix multiplication algorithm.A performance analysis is presented in Section 3.The study is concluded in Section 4.
1 Preliminaries
1.1 The diffusion method on bipartite graphs
A bipartite graph can be used to represent the input of a recommender system.In the bipartite graph:the vertexes are consisted of two sets:users U={U1,U2,…,Um} and items I={I1,I2,…,In} respectively.The user-item relation can be described by an adjacent matrix A.If Uihas used Ij:set A(i,j)=1:otherwise A(i,j)=0.Fig.1 shows an illustration consisting of three users and five items.
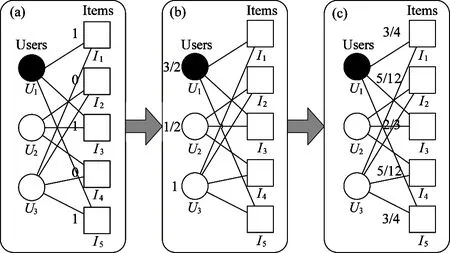
Fig.1 Illustration of the diffusion process on a bipartite graph
Suppose that a kind of resource is initially located on items.Each item will averagely distribute its resource to all connected users:and then each user will redistribute the received resource to connected items.Plot (a) shows the initial condition given U1as the target user:and plot (b) describes the result after the first step diffusion:during which the resources are transferred from items to users.Eventually:the resources flow back to items:and the result is shown in plot (c).
Denoting r(0)as the initial resource vector on items.rjis the amount of resource located on Ij.The final resource vector after the two-step diffusion[6]is shown in
(1)
(2)
In this case:the initial resource can be understood as giving a corresponding recommending capacity to each connected item based on history records:and the different initial resource vectors for different users have captured the personalized preferences.The final resource vector r(2)(Ui) is obtained by Eq.(1).Ui’s unconnected items are sorted in descent order based on final resource values.Items with the highest values are recommended.This algorithm was originally motivated by the resource-allocation process on graphs:and has been shown to be more accurate than traditional collaborative filtering based on MovieLens data set[15].
1.2 MapReduce computing model
MapReduce is a parallel computing model[12].It splits an input data set into several parts.Each mapper deals with one part:produces key/value pairs and writes them into the intermediate files.The key/value pairs are partitioned and emitted to reducers to calculate the final result.In this work:all implementations are based on the Hadoop platform.
2 MapReduce based computation of the diffusion method
2.1 Vectorization of the diffusion method
The diffusion result is calculated by summation as shown in Eq.(1).Such formation is not convenient for parallel processing.Vectorization of the diffusion process would facilitate the parallel computation.
In the first step of diffusion:resources are transferred from items to users.The transition matrix is
T(1)=AT./KI
(3)
where ATdenotes the transpose of A:and “./” performs the right-array division by dividing each element of ATby the corresponding element of KI.KIis an n×m matrix as shown in Eq.(4).The elements in row j are initialized to k(Ij).
(4)
After the first step:the resource vector on Uiis r(1)(Ui)=r(0)(Ui)·T(1).
Similarly:the transition matrix in the second step of diffusion is
T(2)=A./KU
(5)
KUis an m×n matrix as shown in Eq.(6).The elements in row i are initialized to k(Ui).
(6)
Finally:the resources on each item are shown in Eq.(7):which is the vectorization result of Eq.(1).
r(2)(Ui)=r(1)(Ui)·T(2)
=r(0)(Ui)·T(1)·T(2)
(7)
The computation complexity of a recommendation process for a target user is O(mn) based on Eq.(1) or Eq.(7).It is impossible to do online computation when the data set is in large scale.So one should employ offline computation to make recommendation for each user.In order to compute the diffusion results of all users:Eq.(7) can be extended to the cascade matrix multiplication format as shown in Eq.(8):where F is the diffusion result of all users in matrix form.
F=A·T(1)·T(2)
(8)
Therefore a cascade matrix multiplication approach is adopted to perform the diffusion computation task.In the next section:the MapReduce framework will be used to design an efficient matrix multiplication algorithm.
2.2 Parallelism of matrix multiplication
Eq.(8) entails three matrix-matrix multiplications.So the core of the diffusion method is to do the matrix multiplication in parallel.In this section:the single tuple method (STM)[13]based on the MapReduce framework is the first to be introduced.Then a dynamic vector based method (DVBM) is which can decrease the CPU and I/O cost effectively.further improvement is made for DVBM by block partitioning.In addition:the order of matrix multiplication is also taken into consideration.
2.2.1 Single Tuple Method
Suppose A is an m×t matrix and B is a t×n matrix.Then the elements of matrix C=A·B can be calculated as
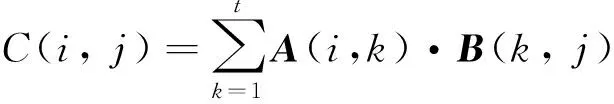
(9)
So an element of matrix C can be got by the inner product of the corresponding row vector in matrix A and column vector in matrix B as shown in Fig.2.

Fig.2 Matrix multiplication in STM
In recommender systems:the user history records are usually in a three-tuple format {Ui,Ij,value}:which are the cases both in MovieLens and Jester data sets.Based on this input format:the MapReduce process of the STM is shown in Table 1.
In the map procedure:{i,k,A(i,k)} and {k,j,B(k,j)} denote the original input format of matrix A and matrix B respectively.〈{i,j },{0,k,A(i,k)}〉 and 〈{i:j},{1,k,B(k,j)}〉 denote the intermediate key/value pairs used for sort and shuffle.Each 〈{i:j},{0,k,A(i,k)}〉 is emitted by n times:while 〈{i:j},{1,k,B(k:j)}〉 is emitted by m times.0 in {0,k,A(i,k)} indicates it is from matrix A:and 1 in {1,k,B(k:j)} indicates it is from matrix B.In the reduce procedure:C(i:j) is obtained as described in Eq.(9).

Table 1 MapReduce algorithm of STM
2.2.2 Dynamic vector based method
However:when the STM on MovieLens-1M data set is taken:it can’t be completed in rational time.It is of time consuming because the elements in the matrices are read or written one by one.There are d(A)·mt+d(B)·tn elements to read and (d(A)+d(B))·mtn elements to write in the map procedure:where d(·) denotes the density of the corresponding matrix.That also means there are (d(A)+d(B))·mtn intermediate elements to sort and shuffle:which is both CPU and I/O consuming.
If the elements could be read or written in batch:the CPU and I/O cost would decrease.Based on this idea:a dynamic vector based method is proposed to decrease the frequency of read and write:so as to reduce the CPU and I/O cost.
The elements are compressed in the same row or column into a single vector.The vectors are stored in different formats according to their density.Take a row vector as an example.If the density is larger than β:the vector is in an array format; otherwise:it is in a key/value format as shown in Eq.(10).β is a parameter that controls the density threshold.In the following experiments:set β=50%.Let i be the row index.Ac(i,:) denotes the compression format of row i in matrix A.The second element in a vector represents the compression type.0 indicating the vector is in an array format:and 1 indicates a key/value format.kv(1≤v≤w) denotes the index of nonzero elements in the row.
Ac(i,:)=
(10)
DVBMcontainstwoMapReducejobsasshowninTable2.TheaimofthefirstMapReducejobistocompressthematrixfromtheoriginthree-tupleformattoavectorformat.Inthemapprocedure:eachelementis

Table 2 MapReduce algorithm of DVBM
emitted according to its row number or column number.In the reduce procedure:the reducer collects elements that belong to the same row or column and compresses them into a row or column vector based on Eq.(10).
In the second job:the compressed vector can be taken as input to implment the matrix multiplication.In the map procedure:Ac(i,:) and Bc(:,j) are read and mapped to 〈{i,j},{0,Ac(i,:)}〉 and 〈{i,j},{1,Bc(:,j)}〉.Each 〈{i,j},{0,Ac(i,:)}〉 is emittedntimes:while 〈{i,j},{1,Bc(:,j)}〉 is emittedmtimes.In the reduce procedure:Ac(i,:) and Bc(:,j) are decompressed to A(i,:) and B(:,j).C(i,j) is obtained as described in Eq.(9).
2.2.3 Dynamic vector based method with block
In DVBM:each reducer only involves two vectors.This does not make full use of the computing power of each worker.More vectors can be allocated to a reducer:which can help decrease the copy frequency in the map procedure.When the copy frequency cuts down:the CPU and I/O cost would both decrease.
Based on the above idea:matrix A is partitioned into several sub-matrices by row:and matrix B is partitioned into several sub-matrices by column as shown in Fig.3.Each sub-matrix is called a block.The term block is also used in file systems where it refers to a unit of storage space:which is not the case in this paper.We can map the rows and columns in the same block to a single reducer:and calculate the elements of matrix C in batch.
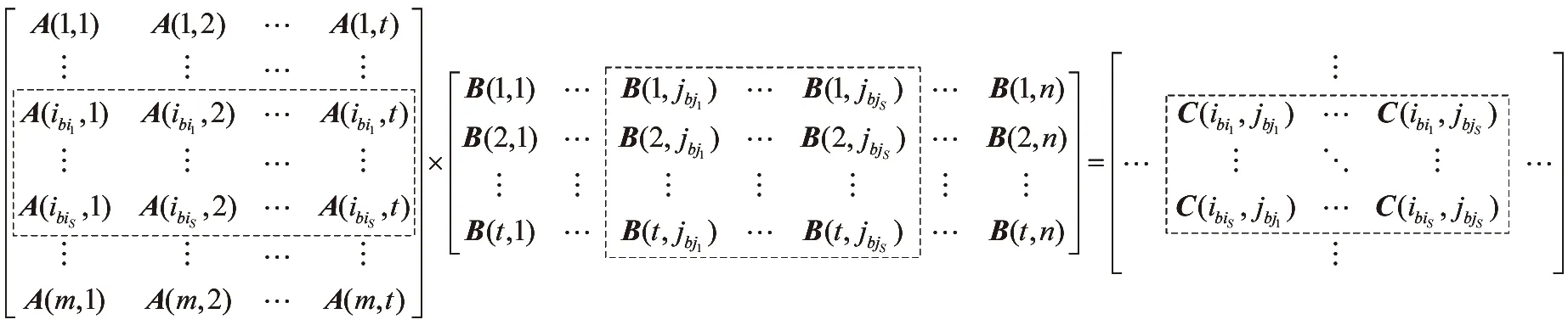
Fig.3 Matrix multiplication in DVBMwB
LetSbe the block size.BI denotes block index:and NB denotes the number of blocks.Then the relations between row/column index and block index can be expressed by Eq.(11) and Eq.(12).The number of blocks can be calculated by Eq.(13) and Eq.(14).
BI(Ac(i,:))=i/S
(11)
BI(Bc(:,j))=j/S
(12)
NB(A)=(m+1)/S;S>1:m>0
(13)
NB(B)=(n+1)/S;S>1:n>0
(14)
The Dynamic Vector Based Method with Block (DVBMwB) just modifies the second job of DVBM as shown in Table 3.In the map procedure:each Ac(i,:) is emitted NB(B) times:while each Bc(:,j) is emitted NB(A) times:which reduces substantial copy cost and I/O cost compared to the DVBM.In the reduce procedure:Ac(i,:) and Bc(:,j) are decompressed to A(i,:) and B(:,j) in batch:and C(i,j) is obtained by the same way as DVBM.

Table 3 MapReduce algorithm of DVBMwB
2.2.4 The order of matrix multiplication
The sequence by which multiplications are done also affects the performance of Eq.(8).An in-order calculation sequence yieldsO(|U|2|I|) time complexity:whereas a reversed order leads toO(|U||I|2).The decision should be based on the relative sizes of the user set and item set.When the number of users is larger:anO(|U||I|2) result is obviously more favorable:or vice versa.
3 Experiment
3.1 Experimental environment
A Hadoop cluster with 3 PCs is constructed.Each machine has a 4-core 2.40GHz Xeon(R) processor:4G memories.The Hadoop version is 1.2.1.
3.2 Data description
In this study:two representative data sets are used:MovieLens-1M and Jester:to evaluate the proposed MapReduce algorithm.MovieLens data sets are collected from the MovieLens web site.Ken Goldberg from UC Berkeley released the Jester data set from the Jester Joke Recommender System.The features of each data set are shown in Table 4.It contains the user number:item number:rating number and density of each data set.These two data sets are of quite different density:which can provide more comprehensive verification to our methods.
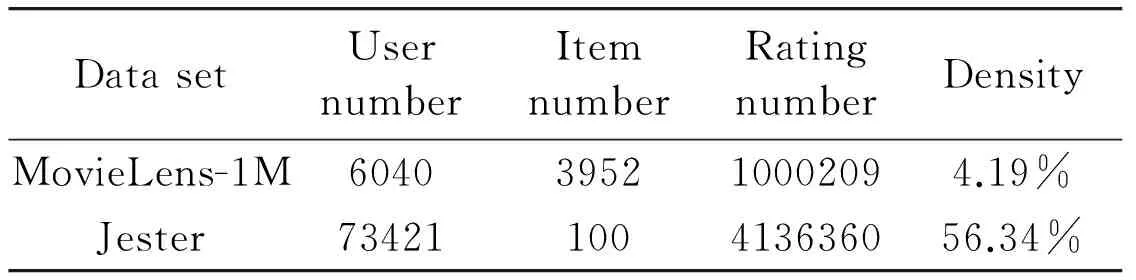
Table 4 Features of the data sets
3.3 Comparison and Analysis
The performance of STM:DVMB and DVMBwB is compared and the compression ratio of the dynamic vector is also measured.After that:the performance of DVMBwB is evaluated with different block sizes on MovieLens-1M and Jester data sets:and also some experiments are conducted to verify that the order of matrix multiplication is very important.
3.3.1 STM vs DVMB vs DVMBwB
As STM cannot complete the diffusion-based recommendation for MovieLens-1M and Jester data sets in a reasonable time:several easier tasks of different user/item dimensions and matrix densities are generated so as to compare the performance of STM:DVMB and DVBMwB.The user/item dimensions include 200×200 and 400×400:while the matrix densities are 5% and 10%.The results are shown in Table 5.The “intermediate matrix density” is the density of the matrix that comes out after the first step of diffusion.It’s usually of high density compared with the original input matrix:which leads to more time consumption in the second step of diffusion.The block size of DVBMwB is 100.
It is seen that DVMB and DVMBwB perform much better than STM.The main factor that affects the CPU and I/O cost is the read/write frequency.On one hand:the decrease of the read/write frequency would improve the I/O efficiency.Too many read/write operations will lead to additional communication overhead in the MapReduce framework.On the other hand:as the number of intermediate elements is equal to the write frequency of the map procedure:less CPU time to sort and shuffle is required if the write frequency goes down.The frequency difference of STM:DVBM and DVBMwB mainly comes from the matrix multiplication job’s map procedure.As analyzed in Section 2.2.1:the read/write frequencies of the map procedure in STM are d(A)·mt+d(B)·tnand (d(A)+d(B))·mtnrespectively.In DVBM:the read and wirte frequencies of the first job are both d(A)·mt+d(B)·tn.However:the read frequency is reduced to m+n and the write frequency is reduced to 2mnin the second job.The difference of DVBM and DVBMwB only comes from the write frequency of the second job’s map procedure.It is reduced to NB(B)·m+NB(A)·n.Although it takes two jobs to complete the matrix multiplication calculation in DVBM and DVBMwB:the total read/write frequencies are cut down compared with the STM algorithm:and the number of intermediate elements also decreases dramatically which saves a large amount of CPU time.Besides:the dynamic vector format also eliminates some redundant information compared with the origin three-tuple format:which can further reduce the I/O cost.So it is quite worthwhile to take an extra step to compress the matrices into vectors.The performance of STM in Table 5 confirms the above analysis.Meanwhile:DVMBwB takes much less time than DVBM:which indicates that block partitioning can help improve the performance effectively.
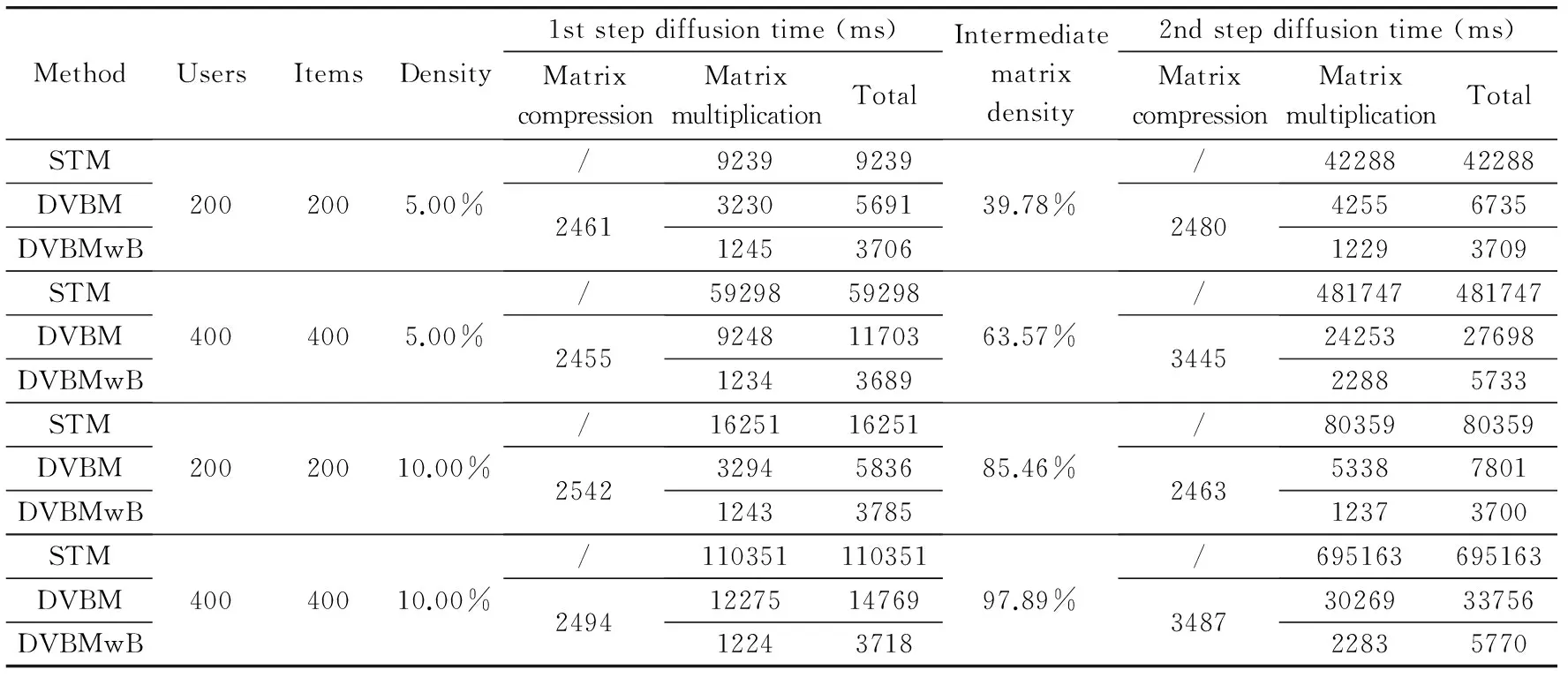
Table 5 Comparison of STM:DVBM and DVBMwB
3.3.2 Compression ability of dynamic vector
The sizes of MovieLens-1M and Jester data sets before and after compression are illustrated in Table 6.The compression ratio is also calculated.It is obvious that the dynamic vector proposed in this paper can compress the data effectively.
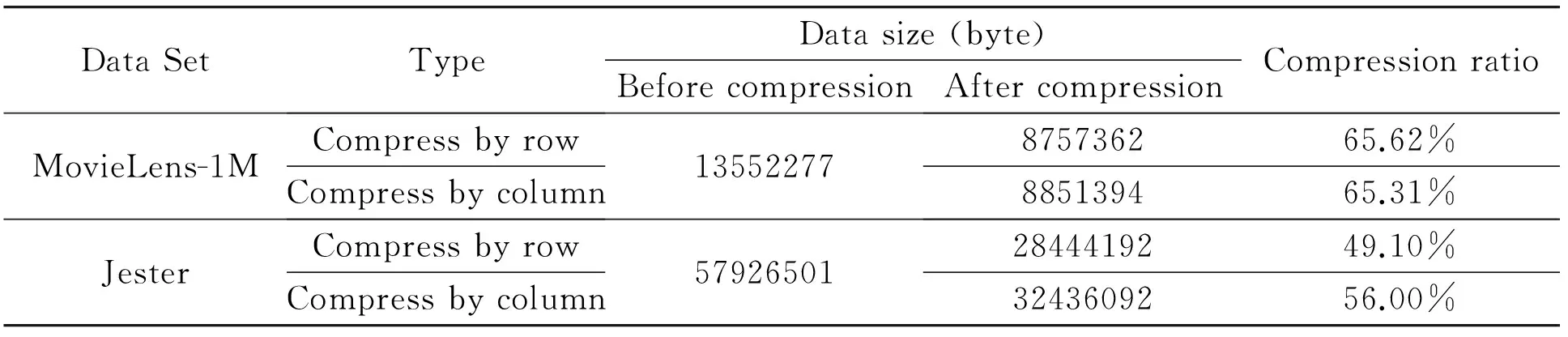
Table 6 Compression results on MovieLens-1M and Jester
Compression experiments is taken on two manually generated data sets of different densities.The dimensions of the generated data sets are 1000×1000 and 2000×2000.The density ranges from 10% to 100%.The relation between the matrix density and compression ratio is illustrated in Fig.4.When the density is more than 50%:the compression ratio gets much better/smaller.The more density a data set has:the better compression ratio we would have.
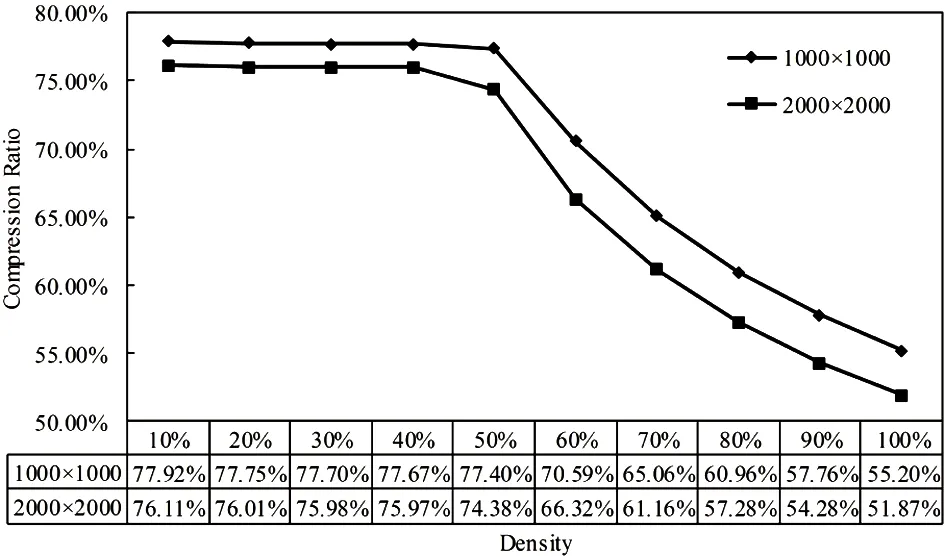
Fig.4 Relation between density and compression ratio
3.3.3 Impact of block size
In DVBMwB:as the block size increases:the copy cost and I/O cost would decrease.However:the block size can’t be too large because of the memory limitation of a single computer.Experiments are taken on MovieLens-1M and Jester data sets with different block sizes.The results are shown in Table 7.As the user number of MovieLens-1M and Jester are both bigger than the item number:the last two matrices are multiplied first so as to get a better performance.
The time used for matrix compression is the same for all block sizes.The differences only come from the matrix multiplication procedure.When the block size is small:it is the copy and I/O cost that lead to the rise of completion time.As the block size gets larger:the calculation speed would not increase all the time.It would slow down or get even worse because of memory shortage.So it is necessary to determine a proper block size based on the servers and data sets under production workloads.
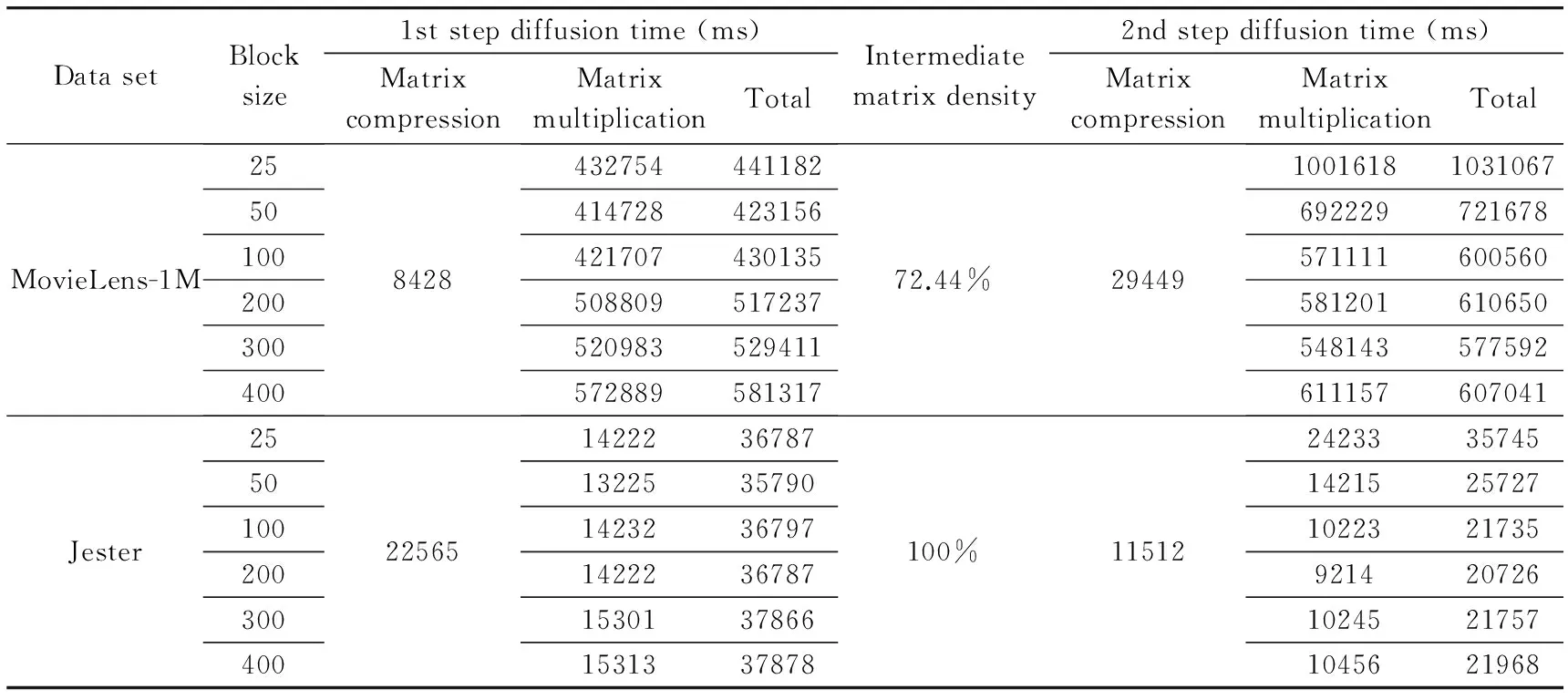
Table 7 DVBMwB of different block size on MovieLens-1M and Jester
3.3.4 Impact of the order of matrix
In the previous sections:the matrix multiplication is done in reversed order.In order to display the influence of the order of matrix multiplication:the order of matrix multiplication on MovieLens-1M data set is changed.The block size used here is 100.The time used for matrix compression and matrix multiplication would both rise if we do the diffusion computation in order as shown in Fig.5 and Fig.6.Besides:the intermediate matrix density would also increase from 72.44% to 95.8% according to the experiment.
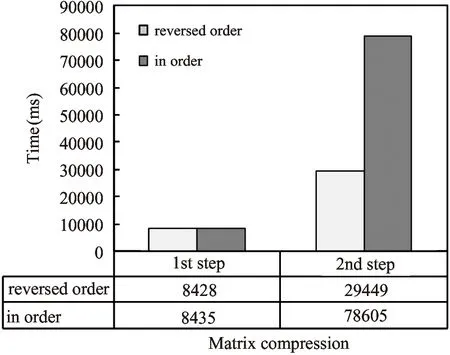
Fig.5 Matrix compression time on MovieLens-1M
4 Conclusion
In this study:a parallel version of a classic diffusion algorithm is proposed on MapReduce framework.The diffusion method is transformed to the cascade matrix multiplication format so as to implement it in the MapReduce computing model.
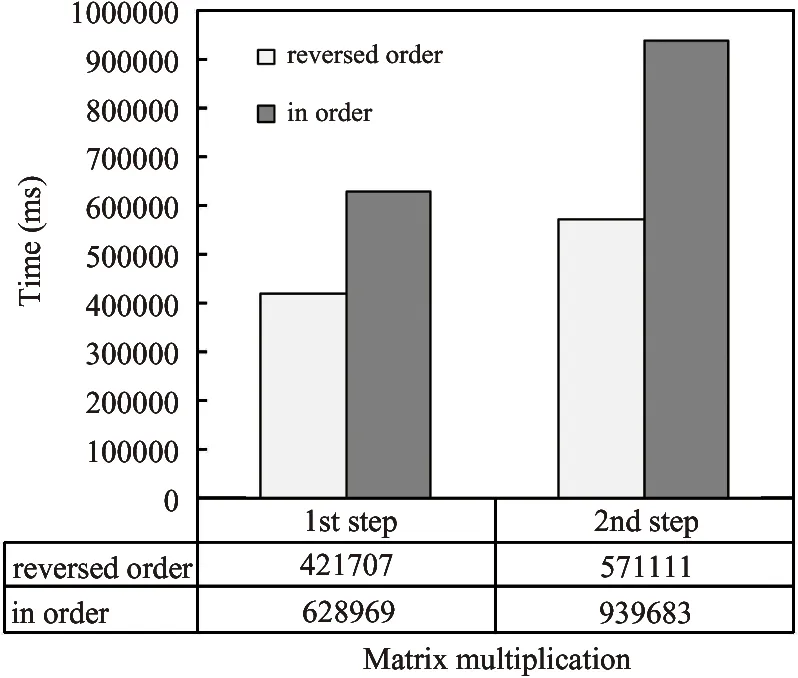
Fig.6 Matrix multiplication time on MovieLens-1M
A novel dynamic vector based matrix multiplication algorithm is designed on the MapReduce framework:which can improve the performance effectively.It can be also applied to other matrix multiplication scenarios.Comprehensive experiments are conducted to verify the effectiveness of our method.The block size and the order of matrix multiplication both have influence on the time cost of diffusion computation.
In the future:our matrix multiplication method will be extended on the MapReduce framework to some other graph-based circumstances.Besides:some large-scale computation frameworks:like GraphLab[16]will be also studied.
[1] Bobadilla J:Ortega F:Hemando A:et al.Recommender systems survey.Knowledge-BasedSystems:2013:46(1):109-132
[2] Linden G:Smith B:York J.Amazon.com recommendations:Item-to-item collaborative filtering.InternetComputing:2003:7(1):76-90
[3] Bennett J:Lanning S.The netflix prize.In:Proceedings of the 2007 KDD Cup and Workshop:California:USA:2007.35
[4] Shi Y:Larson M:Hanjalic A.Collaborative filtering beyond the user-item matrix:A survey of the art and future challenges.ACMComputingSurveys:2014:47(1):3
[5] Huang Z:Chen H:Zeng D.Applying associative retrieval techniques to alleviate the sparsity problem in collaborative filtering.ACMTransactionsonInformationSystems:2004:22(1):116-142
[6] Zhou T:Ren J:Medo M:et al.Bipartite network projection and personal recommendation.PhysicalReviewE:2007:76(4):70-80
[7] Zhang Y C:Medo M:Ren J:et al.Recommendation model based on opinion diffusion.EurophysicsLetters:2007:80(6):417-429
[8] Long G:Zhang G:Lu J:et al.Scaling-up item-based collaborative filtering recommendation algorithm based on Hadoop.In:Proceedings of the 2011 IEEE World Congress on Services:Washington:USA:2011.490-497
[9] Zhao Z D:Shang M S.User-based collaborative-filtering recommendation algorithms on Hadoop.In:Proceedings of the Third International Conference on Knowledge Discovery and Data Mining:Phuket:Thailand:2010.478-481
[10] Shvachko K:Kuang H:Radia S:et al.The hadoop distributed file system.In:Proceedings of the 26th Symposium on Mass Storage Systems and Technologies:Incline Village:USA:2010.1-10
[11] Schelter S:Boden C:Markl V.Scalable similarity-based neighborhood methods with mapreduce.In:Proceedings of the 6th ACM Conference on Recommender Systems:New York:USA:2012.163-170
[12] Dean J:Ghemawat S.MapReduce:simplified data processing on large clusters.CommunicationsoftheACM:2008:51(1):107-113
[13] Li L N:Li C P:Chen H:et al.MapReduce-based simrank computation and its application in social recommender system.In:Proceedings of the 2013 IEEE International Congress on Big Data:Santa Clara:USA:2013.133-140
[14] Zheng J H:Zhang L J:Zhu R:et al.Parallel matrix multiplication algorithm based on vector linear combination using MapReduce.In:Proceedings of the IEEE 9th World Congress on Services:Santa Clara:USA:2013.193-200
[15] Zhang Z K:Zhou T:Zhang Y.Personalized recommendation via integrated diffusion on user-item-tag tripartite graphs.PhysicaA:StatisticalMechanicsandItsApplications:2010:389(1):179-186
[16] Kyrola A:Blelloch G:Guestrin C.GraphChi:Large-scale graph computation on just a PC.In:Proceedings of the 10th USENIX Symposium onOperating Systems Design and Implementation:California:USA:2012.31-46
Peng Fei:born in 1988.He is currently pursuing his Ph.D.degree in the National Network New Media Engineering Research Center:Institute of Acoustics:Chinese Academy of Sciences and the University of Chinese Academy of Sciences.He received his B.S.degree from the department of Electronics and Information Engineering in the Huazhong University of Science and Technology in 2010.His research interests include new media technologies and recommender systems.
10.3772/j.issn.1006-6748.2016.03.008
①Sponsored by the National High Technology Research and Development Program of China (No.2011AA01A102):the Key Program of the Chinese Academy of Sciences (No.KGZD-EW-103-2).
 High Technology Letters2016年3期
High Technology Letters2016年3期
- High Technology Letters的其它文章
- Antenna selection based on large-scale fading for distributed MIMO systems①
- Real-time vehicle tracking for traffic monitoring systems①
- A survey of occlusion detection method for visual object①
- Concurrent processes scheduling with scarce resources in small and medium enterprises①
- Real-time video compression system design and hardware implementation based on multiple ADV212①
- Forming mechanism of ink layer on the printing plate in inking process and influencing factors of its thickness①
