Antenna selection based on large-scale fading for distributed MIMO systems①
Shi Ronghua (施荣华):Yuan Zexi:Dong Jian:Lei Wentai:Peng Chunhua
(School of Information Science and Engineering:Central South University:Changsha 410083:P.R.China)
Antenna selection based on large-scale fading for distributed MIMO systems①
Shi Ronghua (施荣华):Yuan Zexi:Dong Jian*To whom correspondence should be addressed.E-mail:dongjian@csu.edu.cnReceived on June 6,2015:Lei Wentai:Peng Chunhua
(School of Information Science and Engineering:Central South University:Changsha 410083:P.R.China)
An antenna selection algorithm based on large-scale fading between the transmitter and receiver is proposed for the uplink receive antenna selection in distributed multiple-input multiple-output (D-MIMO) systems.By utilizing the radio access units (RAU) selection based on large-scale fading:the proposed algorithm decreases enormously the computational complexity.Based on the characteristics of distributed systems:an improved particle swarm optimization (PSO) has been proposed for the antenna selection after the RAU selection.In order to apply the improved PSO algorithm better in antenna selection:a general form of channel capacity was transformed into a binary expression by analyzing the formula of channel capacity.The proposed algorithm can make full use of the advantages of D-MIMO systems:and achieve near-optimal performance in terms of channel capacity with low computational complexity.
distributed MIMO systems:antenna selection:particle swarm optimization:large-scale fading
0 Introduction
Multi-input multi-output (MIMO) technique can improve the reliability of transmission and channel capacity exponentially without extra bandwidth[1].For traditional centralized antenna systems:due to the inter-cell interference:the spectral and energy efficiencies remain low:especially at the cell edges.Recently:a distributed antenna system (DAS) as a promising candidate for future wireless communications has got wide attention for the reason that it can provide power saving:extend coverage and increase system capacity[2].Distributed MIMO (D-MIMO) systems:which combine the advantages of MIMO systems and DAS:can obtain better performance than traditional co-located MIMO (C-MIMO) systems[3,4].In a typical D-MIMO system:radio access units (RAUs) equipped with a number of antennas are deployed on the distributed system over a large area and connected to a central unit (CU).Relying on its distributed construction:D-MIMO systems can not only inherit the advantages of DAS which decreases path loss and overcomes shadow effect:but also improve capacity performance remarkably.
Generally:MIMO systems should have the same number of radio frequency chains as the number of antennas at both transmitter and receiver:which dramatically increases additional hardware costs and system complexity.In order to solve this problem:antenna selection technologies have been proposed at the right moment:which only use a subset of transmit and/or receive antennas with the best channel condition to communicate and it achieves excellent performance with fewer radio frequency chains and decreases the complexity and hardware cost of MIMO systems.In recent years:a number of studies have been done on antenna selection techniques and several antenna selection algorithms have been proposed[5-10].The optimal antenna selection algorithm:namely exhaustive search algorithm (ESA):is an exhaustive search of all possible combinations for locating the best antenna subset[5].However:the required computational complexity grows exponentially with the number of antennas:which is unaffordable for antenna selection problem in practical scenarios.In view of this:several suboptimal antenna selection algorithms are proposed:such as the norm-based selection algorithm (NBS)[6]:norm and correlation based algorithm (NCBA)[10].These algorithms used in traditional C-MIMO systems can be applied directly into D-MIMO systems.However:in the C-MIMO systems:the antenna distance between the user terminal (UT) and the base station (BS) are equal so that path losses in the large-scale fading are not considered.On the contrary:the antenna distance between the UT and the RAUs are unequal in the D-MIMO systems so that path loss becomes an important factor to be considered.
In order to make use of the full advantages of D-MIMO systems:a near-optimal antenna selection algorithm is proposed in this paper based on large-scale fading for D-MIMO systems:which combines improved particle swarm optimization (PSO) algorithm with large-scale fading based RAU selection.Taking account of the large-scale fading:the proposed algorithm shows remarkable capacity performance and low computational complexity.Simulation results confirm that its capacity performance approaches that of the exhaustive search algorithm and is better than the previous algorithms.
The rest of paper is organized as follows.In Section 1:the D-MIMO system model is illustrated.In Section 2:a binary expression of channel capacity is introduced and a near-optimal antenna selection algorithm based on large-scale fading is presented to optimize the binary expression of channel capacity.Simulation results are presented in Section 3 and final conclusions are given in Section 4.
Notation.Throughout this paper:for matrix A:AT:AH:and det(A) denote the transpose:complex conjugate transpose:and the determinant of A:respectively.The termsa×brepresent the (a×b)-dimensional space with complex valued elements.
1 Distributed MIMO system models
It is considered that a (M:N:L) D-MIMO system where a central unit (CU) connects toN= 5 RAUs via high-speed:less-delay and error-free channels such as optical fiber links.Each RAU is equipped withLantennas that serve UT withMantennas:shown in Fig.1.The signal information is transmitted between CU and RAUs.Assume all processes are perfectly synchronized.
It is assumed that the communication band is narrow enough to have a flat response across the frequency band:and signal model is linear time-invariant.The received signal parameterized by the distance vector d is given as Ref.[2]
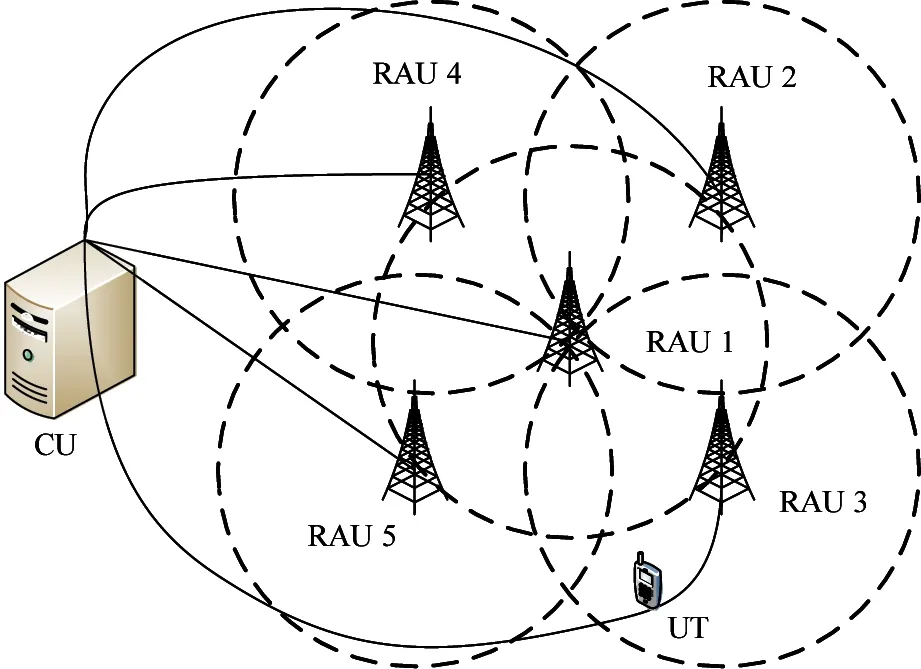
Fig.1 Distributed MIMO system model
r(t,d)=H(d)·s(t)+z(t)
(1)
(2)
where Hn(dn)∈M×Lis the channel matrix from the UT tonth RAU:and can be expressed as
(3)
(4)

2 Antenna selection algorithm
2.1 Binary expression of channel capacity
In order to apply the improved PSO algorithm better in antenna selection:the general form of channel capacity is transformed into a binary expression by re-deriving the formula of channel capacity.


(5)

Let anNL×NLdiagonal matrix Δ be used for antenna selection atNRAUs:which is represented as
(6)


(7)
As a result:the antenna selection problem becomes a combinatorial optimization problem on obtaining appropriate Δ and maximizing the channel capacity (Eq.(7)).
2.2 RAU selection based on large-scale fading
So far:a few schemes have discussed on the RAU selection problem in D-MIMO systems.The scheme in Ref.[11] computes the Euclidean norms of channel matrix:and selects all antennas from the RAU which contains the maximal Euclidean norm as the optimal transmission antennas.This scheme ignores the possibility that some antennas in other RAUs have better performance than those in RAU with the maximal Euclidean norm.
In this paper:a more effective RAU selection scheme has been proposed for the characteristic of distribution in D-MIMO systems.In this scheme:Poptimal RAUs are selected from theNavailable ones to reduce the number of selectable antennas greatly so as to decrease the computational complexity of selection.SinceNavailable RAUs with a number of antennas have been distributed into the small cells:the total antennas in all RAUs can be decreased by the large-scale fading between different RAUs and UT.So the following antenna selection will be performed with onlyP×Lcandidate antennas.
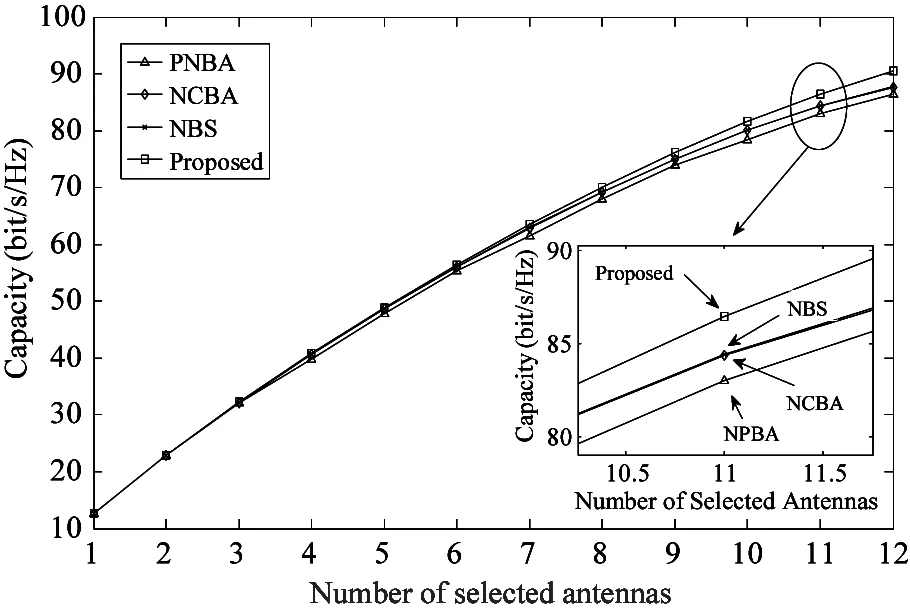
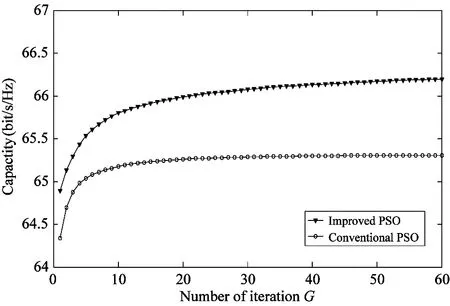
The RAU selection is a norm-based approach:which compares the norm of all antennas and picks out theKmaximal values one by one:whereKdenotes the number of the required optimal antennas.Then:Poptimal RAUs is found out that theseKantennas are involved inNavailable RAUs to build a new candidate set and the channel matrix H(d)∈NL×Mcan be transformed as Hp∈PL×M.Generally:since the large-scale fading has a significant effect on the composite fading channel coefficient(dn) in Eq.(4) under differentdn:the antennas will obtain better CSI with a better large-scale fading coefficient:and vice versa.So theseKantennas will hardly be involved in every RAU at the same time:i.e.:P Table 1 Antenna RAU selection algorithm.The complexity corresponding to each part of the algorithm is shown in the right column StepManipulationComplexity1RAUSelection(M,N,L,K,h1,h2,…,hNL) 2Ω:={1,2,…,NL} 3χ:={1,2,…,N} 4H:=[h1,h2,…,hNL]H 5S:=Ω 6forj:=1toNL 7 αj:=hHjhjO(MNL)8end 9forn:=1toK 10 J:=argmaxj∈ΩαjO(MNK)11 Q:=⌊JL」 12 ifQ∈χ 13 χ:=χ-{Q} 14 end 15 Ω:=Ω-{J} 16end 17fori:=1tolength[χ] 18r:=χ[i] 19S:=S-{r,r+1,…,r+L} 20end 21returnS 2.3 Particle swarm optimization algorithm based on large-scale fading In this section:an antenna selection scheme that utilizes particle swarm optimization (PSO) has been presented.PSO is a collaborative computational technique derived from the social behavior of bird flocking and fish schooling[12].PSO is found that it has a huge advantage in solving global optimization problems:thus it can be applied to solve the antenna selection problem[13]. (8) where W is aD×Ddiagonal matrix of large-scale fading, (9) where wi∈(0,1):i=1,2,…,D:widenotes the large-scale fading on thei-th antenna:which is normalized by the maximum of large-scale fading coefficient. Secondly:the selection of antennas is represented by a binary diagonal matrix (10) where Δiis associated with an available antenna.According to the priority of each antenna:Kantennas with the highest priority are picked out one by one without replacement:and the corresponding Δiis set to 1 while others are set to 0.As a result:by using Eq.(7):the fitness function of thek-th particle is represented as (11) where IDis aD×Didentity matrix:HPis the channel matrix after the RAU selection. The last modification over the conventional PSO is an improvement in updating velocity.Velocity updating formula in conventional PSO is represented as (12) (13) The main steps are as follows. Step 4 If the convergence criteria is satisfied:then terminate.Otherwise go to step 5. For performance comparison:simulation results of the proposed PSO antenna selection scheme in D-MIMO systems are presented and all the results are compared with other antenna selection schemes.The channels are assumed to be quasi-static and statistically independent in the MIMO systems.All the simulations are performed using Monte Carlo runs and each result is an average value with 5000 independent simulation runs. For performance comparison:a D-MIMO system with (M:N:L) set to be (4:6:2) is presented:and the number of uplink receive antennas needed to be selected optimally isK=4.The population sizeQof PSO is 30 and the number of iterationsGis 30.The radius of the circular cell is 1000m:and the distances between the UT and 6 antenna RAUs are 1000m:1500m:2000m:500m:2500m:700m in the coordinate system respectively.In order to show the performance of the proposed algorithm:it is compared with exhausting search algorithm (ESA)[5]:RAU-selection norm-based algorithm (PNBA)[11]:norm and correlation based antenna selection algorithm (NCBA)[10]and norm-based antenna selection algorithm (NBS)[6].Fig.2 shows that 10% outage capacities achieved by these algorithms increase remarkably as SNR increases:while the achievable capacity of the proposed algorithm approaches that of ESA and better than other algorithms for a wide range SNR. Fig.2 Capacity versus SNR with M=4:N=6:L=2, K=4:Q=30:G=30 Moreover:another larger D-MIMO system with (M:N:L) set to be (10:7:4) is considered:and the number of uplink receive antennas needed to be selected optimally isK= 10.The population sizeQof PSO is 30 and the number of iterationsGis 30.The radius of the circular cell is 1000m:and the distances between the UT and 7 antenna RAUs are 1000m:1500m:2000m:500m:2500m:1800m:700m in the coordinate system respectively.Fig.3 shows that 10% outage capacities achieved by these algorithms increase remarkably as SNR increases:while the achievable capacity of the proposed algorithm approaches that of ESA and much better than other algorithms for a wide range SNR. Fig.4 illustrates the performance of the proposed algorithm with PNBA:NCBA:and NBS for different numbers of selected antennas as a function of selected antennasKforM=12:N=7:L=3:Q=30:G=30.SNR is set to 25dB.The radius of the circular cell is 1000m:the distances between UT and 7 antenna RAUs are also 1000m:1500m:2000m:500m:2500m:1800m:700m in the coordinate system respectively.As can be seen from Fig.4:the outage capacity achieved by each algorithm increases substantially with the number of antennasK.The capacity achieved by the proposed algorithm is better than other algorithms for all values ofK.In particular:the advantage of the proposed algorithm will increase continuously with the value ofKcompared with the other algorithms. Fig.3 Capacity versus SNR with M=10:N=7:L=4, K=10:Q=30:G=30 Fig.4 Capacity versus number of antennas K with M=12, N=7:L=3:SNR=25dB:Q=30:G=30. Fig.5 provides some interesting data regarding the performance improvement by applying proposed methods of optimizing population in PSO:withM=11:N=8:L=3:K=11:Q=40.The SNR is fixed at 20dB.It is assumed that the radius of the circular cell is 1000m:the distances between the UT and 8 antenna RAUs are 1000m:800m:1500m:2000m:1200m:500m:2500m:1800m in the coordinate system respectively.The conventional PSO with arbitrary population randomly choses initial population:and updates the population with constant inertia weight.The improved PSO not only optimizes the population initialization with large-scale fading coefficient but also improves the updating of population by utilizing inertia weight based on large-scale fading coefficient.It is observed from the simulation results that the conventional PSO finds its global optimum early and this global optimum is obviously worse than the global optimum obtained by improved PSO.Moreover:the channel capacity obtained by the proposed algorithm is larger than that of conventional PSO.It can be seen that the exploration ability of the proposed algorithm is better than that of conventional PSO with the inertia weightWbased on large-scale fading.Therefore:it can be concluded that the performance of the proposed algorithm generates a considerable improvement over that of conventional PSO. Fig.5 Capacity versus G with M=11:N=8:L=3, K=11:Q=40:SNR=20dB In order to intuitively compare the computational complexity of the aforementioned five antenna selection schemes:the parameters of their computational time (In Table 2) are evaluated by using practical hardware:say the Texas Instruments digital signal processing (DSP) chip C6711:which possesses computational capability of 500 million of multiplications and additions per second (MMACS)[15].It is clear from Table 2 that the proposed algorithm is better in terms of computational complexity than ESA and Gorokhov algorithm:especially with the increase of the antennas.NBS and NCBA require less computation than the proposed algorithm:but their performances of the channel capacity are much worse than that of our proposed algorithm.In such a scenario:except for ESA:the aforementioned four schemes are all suitable to the MIMO system in Ref.[15]:as the computational time of these antenna selection schemes is all lower than the elapsed time of 80ms between two channel matrix measurements.However:as the time between two channel matrix measurements decreases or other antenna selection scenarios are considered:the aforementioned schemes with higher computational time such as the optimum algorithm may encounter some difficulties.Therefore:the proposed algorithm provides a viable alternative to previous work by striking a better tradeoff between performance and computational complexity. Table 2 Comparisons of computational complexity with 500 million multiplications and additions per second In this paper:based on large-scale fading:a modified PSO algorithm is presented combined with norm-based RAU selection for antenna selection in D-MIMO system.The proposed algorithm for the antenna selection requires low computational complexity and the performance approaches that of the exhaustive search algorithm:which makes the best use of the large-scale fading in D-MIMO systems to simplify the antenna selection problem by reducing the number of candidate antennas remarkably.This paper indicates that the proposed algorithm is a suitable candidate for solving complex communication problems in D-MIMO system. [1] Paulraj A J:Gore D A:Nabar R U:et al.An overview of MIMO communications:a key to gigabit wireless.ProceedingsoftheIEEE:2004:92:198-218 [2] Choi W:Andrews J.Downlink performance and capacity of distributed antenna systems in a multicell environment.IEEETransactionsonWirelessCommunications:2007:6:69-73 [3] Sawahashi M:Kishiyama Y:Morimoto A:et al.Coordinated multipoint transmission/reception techniques for LTE-advanced [Coordinated and Distributed MIMO].IEEEWirelessCommunications: 2010:17:26-34 [4] Ibernon-Fernandez R:Molina-Garcia-Pardo J M:Juan-Llacer L.Comparison between measurements and simulations of conventional and distributed MIMO system.IEEEAntennasandWirelessPropagationLetters:2008:7:546-549 [5] Sanayei S:Nosratinia A.Antenna selection in MIMO systems.IEEECommunicationsMagazine:2004:42:68-73 [6] Molisch A F:Win M Z:Yang-seok C:et al.Capacity of MIMO systems with antenna selection.IEEETransactionsonWirelessCommunications:2005:4:1759-1772 [7] Gorokhov A:Gore D A:Paulraj A J.Receive antenna selection for mimo spatial multiplexing:theory and algorithms.IEEETransactionsonSignalProcessing:2003:51:2796-2807 [8] Gore D A:Paulraj A J.MIMO antenna subset selection with space-time coding.IEEETransactionsonSignalProcessing:2002:50:2580-2588 [9] Gharavi-Alkhansari M:Gershman A B.Fast antenna subset selection in MIMO systems.IEEETransactionsonSignalProcessing:2004:52:339-347 [10] Liu S:He Z:Wu W:et al.A fast sub-optimal antenna selection algorithm in mimo systems.In:Proceedings of the Wireless Communications and Networking Conference:Las Vegas:USA:2006.734-739 [11] Su Y Z:Feng G Z.A novel fast antenna selection algorithm in distributed MIMO systems.In:Proceedings of the 12th IEEE International Conference on Communication Technology:Nanjing:China:2010.275-280 [12] Clerc M:Kennedy J.The particle swarm - explosion:stability:and convergence in a multidimensional complex space.IEEETransactionsonEvolutionaryComputation:2002:6:58-73 [13] Naeem M:Lee D C.Near-optimal joint selection of transmit and receive antennas for MIMO systems.In:Proceedings of the 9th IEEE International Symposium on Communications and Information Technology:Icheon:2009.572-577 [14] Porto V W:Saravanan N:Waagen D:et al.Parameter Selection in Particle Swarm Optimization.In:Evolutionary Programming VII:Porto V W:Saravanan N:Waagen D:et al.Springer Berlin Heidelberg:1998.591-600 [15] Wallace J W:Jensen M A:Swindlehurst A L:et al.Experimental characterization of the MIMO wireless channel:data acquisition and analysis.IEEETransactionsonWirelessCommunications:2003:2:335-343 Shi Ronghua:received his B.S.degree in Computer Software from Changsha Railway University in 1986:and his M.S.degree in computer science from Central South University of Technology in 1989.He has been working in the Changsha Railway University since 1989:and is currently a Professor of the Department of Electronic Engineering.His current research interests include computer networks:algorithm and system:broadband ISDN. 10.3772/j.issn.1006-6748.2016.03.001 ①Supported by the National Natural Science Foundation of China (No.61201086:61272495):the China Scholarship Council (No.201506375060):the Planned Science and Technology Project of Guangdong Province (No.2013B090500007) and the Dongguan Project on the Integration of Industry:Education and Research (No.2014509102205).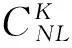

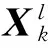
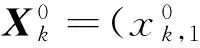
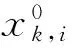
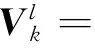
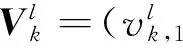
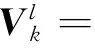
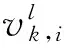
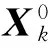
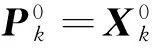


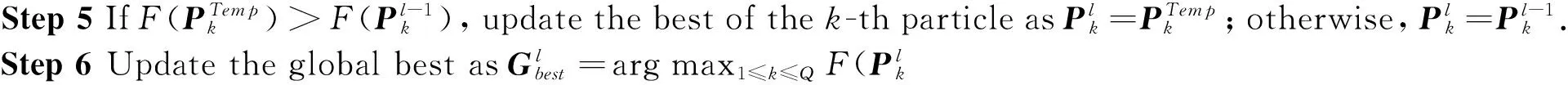
3 Simulation results and discussion


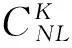

4 Conclusions
 High Technology Letters2016年3期
High Technology Letters2016年3期
- High Technology Letters的其它文章
- Real-time vehicle tracking for traffic monitoring systems①
- A survey of occlusion detection method for visual object①
- Concurrent processes scheduling with scarce resources in small and medium enterprises①
- Real-time video compression system design and hardware implementation based on multiple ADV212①
- MapReduce based computation of the diffusion method in recommender systems①
- Forming mechanism of ink layer on the printing plate in inking process and influencing factors of its thickness①
