Buffer allocation method of serial production lines based on improved ant colony optimization algorithm①

Zhou Binghai (周炳海), Yu Jiadi

(School of Mechanical Engineering, Tongji University, Shanghai 201804, P.R.China)



Buffer allocation method of serial production lines based on improved ant colony optimization algorithm①

Zhou Binghai (周炳海)②, Yu Jiadi

(School of Mechanical Engineering, Tongji University, Shanghai 201804, P.R.China)

Buffer influences the performance of production lines greatly. To solve the buffer allocation problem (BAP) in serial production lines with unreliable machines effectively, an optimization method is proposed based on an improved ant colony optimization (IACO) algorithm. Firstly, a problem domain describing buffer allocation is structured. Then a mathematical programming model is established with an objective of maximizing throughput rate of the production line. On the basis of the descriptions mentioned above, combining with a two-opt strategy and an acceptance probability rule, an IACO algorithm is built to solve the BAP. Finally, the simulation experiments are designed to evaluate the proposed algorithm. The results indicate that the IACO algorithm is valid and practical.

buffer allocation, improved ant colony optimization (IACO) algorithm, serial production line, throughput rate

0 Introduction

The buffer allocation problem (BAP) is a significant optimization problem faced by engineers of manufacturing system, which refers to the way of allocating buffer storage within the production line. While buffers can compensate for the blocking and starving of stations in the production line, inclusion of buffers results in additional costs probably due to increased capital investment, floor space and in-process inventory. Therefore determining appropriate buffer storage sizes is still a challenging problem.

Due to its importance and complexity, several authors have been working on the BAP for many years. Ref.[1] developed a simulated annealing approach for solving BAP in reliable production lines with the objective of maximizing their average throughput. Ref.[2] presented five different search algorithms to solve the BAP of reliable production lines, including the genetic algorithm (GA), tabu search, simulated annealing, myopic and complete enumeration. Ref.[3] proposed an artificial neural network and myopic algorithm based decision support system on reliable production lines. However, the aforementioned literature only focused on reliable production lines. Ref.[4] proposed a quantitative method to determine the buffer size in front of the bottleneck under multi-product. Ref.[5] developed a new efficient simulation model and an experimental cross matrix for serial production lines to determine the optimal buffer size. Ref.[6] and Ref.[7] proposed an exact Markovian model and an approximate analytical method for unreliable serial flow lines to analyze the relationship between throughput and buffer capacity, respectively. But the aforementioned literature only studied an unreliable serial flow line with two workstations and an intermediate buffer. Ref.[8] implemented a combined artificial immune system optimization algorithm in conjunction with a decomposition method to allocate buffers in transfer lines for maximizing economic profit and throughput. Ref.[9] presented a GA and simulation to solve the BAP of flexible manufacturing system. However, the drawback of these meta-heuristics such as GA in solving combinatorial optimization problems is the necessity to set a number of uncertain parameters, which significantly increases the search time and the number of evaluated solutions to find the optimal or near optimal solution. Ref.[10] developed a petri-net based simulation model to study the continuous flow transfer line with three machines and two buffers, and then analyzed the relationship between the equipment reliability and buffer capacity. Ref.[11] presented a local search based degraded ceiling (DC) approach for solving the BAP. However, the objective function may not be a monotone increasing function as the search time goes.

In this paper, an improved ant colony optimization (IACO) algorithm is used to solve the BAP. Recently, the ant colony optimization (ACO) algorithm has been successfully used by many scholars to solve combinatorial optimization problems[12,13]. It has many good features: distribution, positive feedback, and robustness[14]. However, ACO may lead to a local optimal solution. Thus, some corresponding improvements are done to prevent it from local optimization. One is that when the algorithm is stagnated, the pheromone intensity is reset on all paths in order to break out of the stagnation. Secondly, when the near optimal solution is found, some changes will be made by two-opt strategy to get new solutions. Thirdly, an acceptance probability rule of simulated annealing for updating the best solution is combined with the algorithm. Simulation results indicate that the proposed approach can lead to results that are consistent with our expectations.

1 Problem description

In this paper, the BAP in a serial production line with unreliable machines is examined, as depicted in Fig.1, where the rectangles represent machines Mi(i=1,…,k) and the circles indicate buffers Bi(i=1,…,k-1). The assumptions of the BAP in a serial production line are listed as follows: 1) Parts go through each of the machines and buffers in sequence, from machine M1to Mk. 2) The processing times of all parts are constant and equal for all machines, and the transportation time is negligible. 3) Machines are subject to breakdowns. Times to failure and times to repair for machines are exponentially distributed. 4) Machine Miis starved at time t if Mi-1is down and buffer Bi-1is empty; Machine Miis blocked at time t if Mi+1is down and buffer Biis full. 5) The first machine is never starved, and the last machine is never blocked.

Fig.1 Serial production line

To solve the BAP, evaluation and optimization tools are needed. The evaluation tool is used to calculate performance measures of production lines which have to be optimized (e.g., the average throughput). A Dallery-David-Xie (DDX) algorithm is applied which is proposed in Ref.[15] to calculate the throughput rate of all new configurations.

As shown in Fig.2, the principle of DDX algorithm is to decompose ak-machine line L into a set of k-1 two-machine lines. Each line L(i) is composed of an upstream machine Mu(i) and a downstream machine Md(i), separated by a buffer Bi. The procedural form of this method is given as follows:

Fig.2 Decomposition method

Step 1: Initialization:

ru(1)=r1, uu(1)=u1

rd(i)=ri+1, ud(i)=ui+1(i=1,2,…,k)

where ru(i) and uu(i) denote the failure rate and repair rate of the upstream machine, respectively; rd(i) and ud(i) denote the failure rate and repair rate of the downstream machine, respectively; riis the failure rate of machine Mi, ri=1/MTBFi; uiis the repair rate of machine Mi, ui=1/MTTRi; MTBF and MTTR represent the mean time between failures and the mean time to repair, respectively.

Step 2: For any i=2,3,…,k-1:

(1)

uu(i)=x×uu(i-1)+(1-x)×ui

(2)

ru(i)=Iu(i)×uu(i)

(3)

(4)

(5)

where Iu(i) and Id(i) are the ratio of ru(i) to uu(i) and rd(i) to ud(i), respectively; E(i) is the efficiency of line L(i); eiis the isolated efficiency of machine Mi; Ps(i) denotes the probability of downstream machine being starved; ed(i) is the isolated efficiency of downstream machine Md(i).

Step 3: For any i=k-2, k-1…2,1:

(6)

ud(i)=y×ud(i+1)+(1-y)×ui+1

(7)

rd(i)=Id(i)×ud(i)

(8)

(9)

(10)

where eu(i) is the isolated efficiency of upstream machine Mu(i); Pb(i) denotes the probability of upstream machine being blocked.

Step 4:

If Iu(i)≠Id(i):

E(i)=

(11)

(12)

where tu(i) and td(i) denote the processing time of machine Mu(i) and Md(i); Sirepresents the capacity of theith buffer.

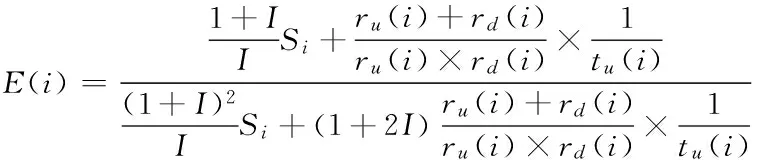
(13)

Step 5: If E(1)=E(2)=…=E(k-1), stop the procedure, otherwise go to step 2.

On the basis of the descriptions mentioned above, the throughput rate of production line is written as follows:

E=f(S)=f(S1,S2,…,Sk-1)

(14)

Therefore, the mathematical model for the BAP can be formulated as follows:

Maximize E=f(S)=f(S1,S2,…,Sk-1)

(15)

Subject to

(16)

0≤Si≤Siup(i=1,…,k-1)

(17)

Sinonnegative integers (i=1,…,k-1)

(18)

where N is the total buffer capacity, which is a fixed nonnegative integer;f(S1,S2,…,Sk-1) is the throughput rate of the production line to be maximized; Siupis the upper bound for each of the buffer locations.

For a production line with k machines and N total buffer capacity, the number of possible buffer allocation configurations can be calculated as follows, which is presented in Ref.[11]:

(19)

As for the optimization tool, it is a search method that tries to find an optimal or a near optimal solution which in our case is the capacity of each buffer in a production line. Therefore, a new optimization method based on IACO algorithm is proposed in the next section.

2 Proposed algorithm

ACO algorithm is a novel biomimetic algorithm. Scholars have solved some difficult problems in discrete system optimization based on the behavior of ants seeking a path between their colony and a source of food[16]. When ants seek for food, the front ones release pheromones on the paths they have visited, then the following ones will randomly choose one path according to the pheromones. When the cycle repeats, the shorter path will have a stronger pheromone trail more quickly. After a certain period of time, all the ants will choose the short trail. The procedure of standard ACO is shown in Fig.3.

As mentioned in introduction, standard ACO may lead to a local optimal solution. In the next sections, details of IACO are provided which is improved by combining with a two-opt strategy and an acceptance probability rule.

Fig.3 Pseudocode of standard ACO

2.1 Encoding

For the BAP, the feasible solution can be expressed as S={S1,S2,…,Sk-1}. It is assumed that there is a certain number of Fipaths in front of theith buffer, where Fi

If 1≤j<(Fi+1)/2:

(20)

If (Fi+1)/2≤j≤Fi:

(21)

(22)

2.2 Initialization

Set the initial buffer allocation Si←N/(k-1) and any remaining resource is placed in the middle location.

2.3 Searching

(23)

where τijis the pheromone intensity on each path; α is a constant.

2.4 Updating

For all the new buffer allocation solutions, throughput rate E can be calculated and the optimal solutions Smaxcan be found among them. Then update the pheromone intensity τij. The update rule is given as follows:

τij←ρ×τij+Δτij， where 1-ρ represents the evaporation of pheromone intensity; Δτijis the pheromone increment in this cycle.

2.5 Two-opt strategy

In order to prevent the algorithm falling into the local optimization, some changes are done in the near optimal solution by the two-opt strategy:

Si←Si-1 and Sj←Sj+1

(24)

Two buffer locations i and j(i, j∈{1,2,…,k-1} and i≠j) are randomly chosen. Then a new buffer solution can be obtained using Eq.(24). For a production line with k machines, the total number of new possible buffer configurations is (k-1)×(k-2).

2.6 Acceptance probability rule

In order to improve the exploring capability of the algorithm, an acceptance probability rule of simulated annealing for updating the best solution is introduced. After a new solution is generated, firstly the objective values of old solution S and new solution S′ should be calculated. If throughput differential ΔE=f(S′)-f(S) is nonnegative, the new solution is accepted as the best solution, otherwise it is accepted with the probability of exp(-ΔE/T), where T is a global time-varying parameter called the temperature.

2.7 Procedure of the IACO

The proposed IACO is formally described as follows:

Step 1: initialize the buffer allocation according to 2.2;

Step 2: initialize the pheromone intensity τij←c and the pheromone increment Δτij←0;

Step 4: evaluate the fitness value according to DDX algorithm and obtain the best solution according to 2.6;

Step 5: perform the two-opt strategy according to 2.5;

Step 6: update pheromone intensity τijof all the paths according to 2.4;

Step 7: if it has led to a local optimal solution, go to step 2, otherwise go on;

Step 8: if the termination criterion is not met, initialize Δτij←0, and go to step 3; otherwise, stop and record the optimal buffer allocation solution S*and its throughput rate E*.

3 Numerical examples

In order to evaluate the applicability of the IACO algorithm, experiments are conducted with serial production line configurations of different total buffer capacities and machines sizes. The experiments results of the proposed IACO and ACO algorithm are compared with those of DC algorithm presented in Ref.[11] and GA presented in Ref.[9]. In all the tests, it is assumed that the processing rate for each machine is one time unit; the values of the algorithm parameters are as follows: α=1, ρ=0.95, γ=100, β=15. Table 1 shows the machine parameters of the production lines. All the experimental studies are programmed in C++ language and run on a PC with Inter (R) Core (TM) 2-Duo (2.00GHz) CPU using the Windows7 operating system.

Table 1 Machines parameters

Table 2 presents the throughput rate, CPU time and number of evaluated solutions by using different optimization methods with k machines (5≤k≤30). It is shown that the IACO algorithm results in slightly larger throughput rate and requires less time and fewer numbers of evaluated solutions to find the near optimal solutions compared with other optimization methods in all of cases.

Table 2 Computational results by different optimization methods

Fig.4 shows the convergence curves of the four algorithms for the production lines with five, fifteen and thirty machines.

It is shown that the throughput rate of near optimal solution increases as the number of evaluated solutions increases for all of the DC, ACO, IACO and GA optimization methods. In addition, the proposed IACO algorithm results in solution quality higher and numbers of evaluated solutions fewer than the other three methods.

For the same number of machines, the different total buffer capacity will lead to a different number of evaluated solutions. Fig.5 shows the effect of the N total buffer capacity to allocate among the production line on the number of the evaluated configurations needed to converge. This test focuses on a production line with ten machines, and the total buffer capacity varies from 90 to 450.

Fig.4 Evolution of the solutions with four methods

Fig.5 Total buffer capacity versus number of evaluated solutions

As shown in Fig.5, the number of evaluated solutions needed by the IACO algorithm is lower than those of the DC, ACO and GA algorithm. In addition, the increase of the total buffer capacity leads to an increase of the number of evaluated solutions for near optimal buffer solutions.

As shown in Fig.6, for six production lines with different sizes (from 5 to 30 machines) and different total buffer capacities, the number of evaluated solutions is increasing as the number of machines increases. In general, the IACO algorithm finds the best configuration much faster than the DC, ACO and GA algorithm.

Fig.6 Influence of the number of machines

Through the experiments analyzed above, it is easily known that the different number of machines and total buffer capacities will lead to a different throughput rate for the production line. As shown in Fig.7, the throughput rate increases with the increase of the total buffer capacity when the number of machines is invariable. However, when the total buffer capacity is invariable, the throughput rate decreases with the increase of the number of machines.

Fig.7 Total buffer capacity and number of machines versus throughput rate

4 Conclusion

In this paper, an IACO algorithm is proposed to solve the BAP with the objective of maximizing the throughput rate in serial production lines with unreliable machines. For the ACO algorithm, some improvements are done to prevent it from local optimization, such as the two-opt strategy and the acceptance probability rule. Comparisons with other widely recognized methods are made to demonstrate the efficiency of our method. The results indicate that the IACO algorithm finds the optimal buffer configuration much faster than the other three approaches for different sizes production lines. Our future work will also test this approach on similar problems especially involving parallel machines.

[1] Spinellis D D, Papadopoulos C T. A simulated annealing approach for buffer allocation in reliable production lines.AnnalsofOperationsResearch, 2000, 93(1-4): 373-384

[2] Papadopoulos C T, O’Kelly M E J, Tsadiras A K. A DSS for the buffer allocation of production lines based on a comparative evaluation of a set of search algorithms.InternationalJournalofProductionResearch, 2013, 51(14): 4175-4199

[3] Tsadiras A K, Papadopoulos C T, O’Kelly M E J. An artificial neural network based decision support system for solving the buffer allocation problem in reliable production lines.Computers&IndustrialEngineering, 2013, 66(4): 1150-1162

[4] Ye T, Han W. A quantitative method to determine the size of the stock buffer in front of the bottleneck under multi-product. In: Proceedings of the 6th World Congress on Intelligent Control and Automation (WCICA), Dalian, China. 2006. 7239-7243

[5] Battini D, Persona A, Regattieri A. Buffer size design linked to reliability performance: A simulative study.Computers&IndustrialEngineering, 2009, 56(4): 1633-1641

[6] Alexandros D C, Chrissoleon P T. Exact analysis of a two-workstation one-buffer flow line with parallel unreliable machines.EuropeanJournalofOperationalResearch, 2009, 197(2): 572-580

[7] Liu J, Yan D, Feng R, et al. Performance evaluation of production lines with unreliable buffer. In: Proceedings of the 8th IEEE International Conference on Control and Automation (ICCA), Xiamen, China, 2010. 350-355

[8] Massim Y, Yalaoui F, Amodeo L, et al. Efficient combined immune-decomposition algorithm for optimal buffer allocation in production lines for throughput and profit maximization.Computers&OperationsResearch, 2010, 37(4): 611-620

[9] Jeong S J, Jung H. Optimal buffer allocation in flexible manufacturing systems using genetic algorithm and simulation.JournalofAdvancedMechanicalDesign,Systems,andManufacturing, 2012, 6(7): 1071-1080

[10] Sörensen K, Janssens G K. Simulation results on buffer allocation in a continuous flow transfer line with three unreliable machines.AdvancesinProductionEngineering&Management, 2011, 6(1):15-26

[11] Nahas N, Ait-Kadi D, Nourelfath M. A new approach for buffer allocation in unreliable production lines.InternationalJournalofProductionEconomics, 2006, 103(2): 873-881

[12] Liao C J, Tsai Y L, Chao C W. An ant colony optimization algorithm for setup coordination in a two-stage production system.AppliedSoftComputing, 2011, 11(8): 4521-4529

[13] Akpinar S, Bayhan G M. Performance evaluation of ant colony optimization-based solution strategies on the mixed-model assembly line balancing problem.EngineeringOptimization, 2014, 46(6): 842-862

[14] Zheng Q X, Li M, Li Y X, et al. Station ant colony optimization for the type 2 assembly line balancing problem.InternationalJournalofAdvancedManufacturingTechnology, 2013, 66(9-12): 1859-1870

[15] Dallery Y, David R, Xie X L. Approximate analysis of transfer lines with unreliable machines and finite buffers.IEEETransactionsonAutomaticControl, 1989, 34(9): 943-953

[16] Kalayci C B, Gupta S M. Ant colony optimization for sequence-dependent disassembly line balancing problem.JournalofManufacturingTechnologyManagement, 2013, 24(3): 413-427

Zhou Binghai, born in 1965. He received his M.S. and Ph.D degrees respectively from School of Mechanical Engineering, Shanghai Jiaotong University in 1992 and 2001. He is a professor, a Ph.D supervisor in School of Mechanical Engineering, Tongji University. He is the author of more than 140 scientific papers. His current research interests are scheduling, modeling, simulation and control for manufacturing systems, integrated manufacturing technology.

10.3772/j.issn.1006-6748.2016.02.001

①Supported by the National Natural Science Foundation of China (No. 61273035, 71471135).

②To whom correspondence should be addrcessed. E-mail: bhzhou@tongji.edu.cnReceived on Feb. 12， 2015