数据子空间对大地电磁二维REBOCC反演结果的影响研究

■吴满　江枭

（1中冶集团武汉勘察研究院有限公司　湖北　武汉　430080；2北京环安工程检测有限责任公司　北京　100082)

数据子空间对大地电磁二维REBOCC反演结果的影响研究

■吴满1江枭2

（1中冶集团武汉勘察研究院有限公司湖北武汉430080；2北京环安工程检测有限责任公司北京100082)

大地电磁二维数据子空间OCCAM算法（REBOCC）是Siripunvaraporn等人编制的将OCCAM反演研究从模型空间转成数据子空间的一种有效实用的大地电磁测深的二维反演算法，从该算法的正反演基本理论出发，通过理论数据的反演实例来说明该反演方法的有效性与可靠性，反演结果也反映出数据子空间的参数选择并不影响最终的反演结果。

大地电磁测深法REBOCC二维反演数据子空间

0　引言

近年来，大地电磁测深（MT）广泛应用于各类地学工程领域，其二维反演方法的研究也随着计算机技术的快速发展而不断深入，如：Constable等[1]提出的OCCAM法则，用线性高斯-牛顿方法得到约束函数的最小值；Smith等[2]提出的快速松弛反演（RRI），用近似灵敏度矩阵来搜索最小约束函数；Rodi等[3]提出的非线性共轭梯度反演（NLCG），用下降方法避免构造大型矩阵等。Siripunvaraporn等[4]在OCCAM反演方法的基础上做出改进，提出数据空间OCCAM反演（DASOCC）和简化基础的OCCAM反演（REBOCC）。REBOCC方法首先把反演问题从模型空间转换到数据空间，把解表示为由模型协方差平滑过的灵敏度矩阵行的线性组合，实现了更块的收敛速度却占用较少的计算机内存，因此在2D大地电磁反演方面能起到很好的成效[5-6]。本文选择单个低阻模型进行反演分别比较TE，TM，TE+TM模式对反演结果的影响以及数据子空间的选择不同对反演效果进行分析。

1　REBOCC反演基本理论

Siripunvaraporn等对经典OCCAM方法改进，将反演思路由模型空间转换到数据子空间，将解表示为由模型协方差平滑过的灵敏度矩阵进行的线性组合，称之为Reduced Basis Occam’s Inversion[4]。这样使得原始的M×M阶的矩阵变为了N×N阶线性方程。同时因为模型参数N比数据M个数要小很多，故而在计算机计算的时候大大减少了CPU运行的时间和对内存的消耗。

一般而言，MT的数据是平滑且繁琐的，因此在数据空间中，不用将所有的灵敏度矩阵作为基函数。对于第k次迭代方程

可以表示成一个光滑的灵敏度矩阵CmJT k行的线性组合：

式中βk+1是基函数的位置展开系数向量。将式（2）代入（1）中，可以得到：

其中Γn是一个N×N阶的数据子空间叉积矩阵。对式（3）中

k β求微分，并另其结果为零，反演过程就变成寻求N个展开系数βk+1，代替了原来M维模型中的系数mk+1。在求解反演之前，从N中找出一个长度为L的子集数据。第k+1次迭代，可表示为：

其中αk+1是简化基的L维未知向量数，Gk是L×M子灵敏度矩阵。由于灵敏度矩阵可由相邻的矩阵插值得到，因此所有的灵敏度矩阵Jk进行可近似表示：

将式（4）和式（5）代入式（1）中可得

式中Γ1 k=CkCmGT

k是N×N阶的数据子空间叉积矩阵[7]。

这样，REBOCC方法的稳定性和有效性依赖于正演模型设置、模型协方差、拉格朗日算子λ-1的一维线性搜索、插值矩阵和静校正。

2　理论数据反演

2.1反演参数选择

为了分析该算法在反演中各参数选择对反演结果的影响，设计一个低阻异常模型（如图1）。

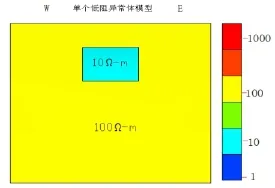
图1　低阻模型示意图

2.2模式选择

以前文设计低阻模型的正演数据来作为理论数据。反演过程都用相同初始模型背景电阻率（100Ω·m），相同频点和测点选择（p=6，测点为36个，两测点间相距3km，频率从1到1000Hz变化）。反演网格和正演一样，均为（含个空气层），反演数据中加入的噪音。

图2为不同模式下同一低阻模型反演效果图。图中红色小框圈中的表示理论模型的大小以及位置，反演结果中三种模式都能较好的突出异常体的形态特征，差别在于不同模式反演出的异常体的位置以及围岩也对异常体的影响有所不同：其中TE模式反演受围岩影响最大，异常大小比模型大，在异常的正下方分别出现相对称的两块高阻异常。TM模式反演受围岩影响相对较小，同样在异常体正下方出现大致对称的两块高阻，形态成瘦长型。TE+TM联合模式反演受围岩影响最小，低阻异常更清楚，在异常正下方同样出现的高阻比单个模式反演要小。由此可得，联合模式相对于单个模式来说反演效果更好，异常更突出，受围岩影响最小。

2.3数据子空间选择

由于大地电磁数据繁多，反演时选择全数据集、全测点集对计算机要求很高，耗时也大，选择合适的频点以及测点数在不影响反演效果的前提下能有效的节省计算机内存以及反演运行时间，也能得到理想的反演效果。

不同测点数而频点数相同情况下（p=6，总测点为36个，相邻两测点间相隔3km，频率从1到1000Hz变化）的反演效果。其他参数设置相同，反演网格与正演选择相同，得到的反演效果如图3。从图中可以看出，测点数不同对反演效果影响不大，只是在异常的下方同样有相对于中心位置有两对称分布的高阻区域，反演过程的不同在于达到期望拟合差的用时不同，测点数选择越多，反演用时越多，(a)、(b)、(c)三种情况都只迭代了四次拟合差就能很好收敛，用时较少，(d)情况下迭代了九次拟合差才收敛到期望值，用时较多。总的来说反演效果都不错，只是在计算用时的差别，测点数选择越多用时越多。

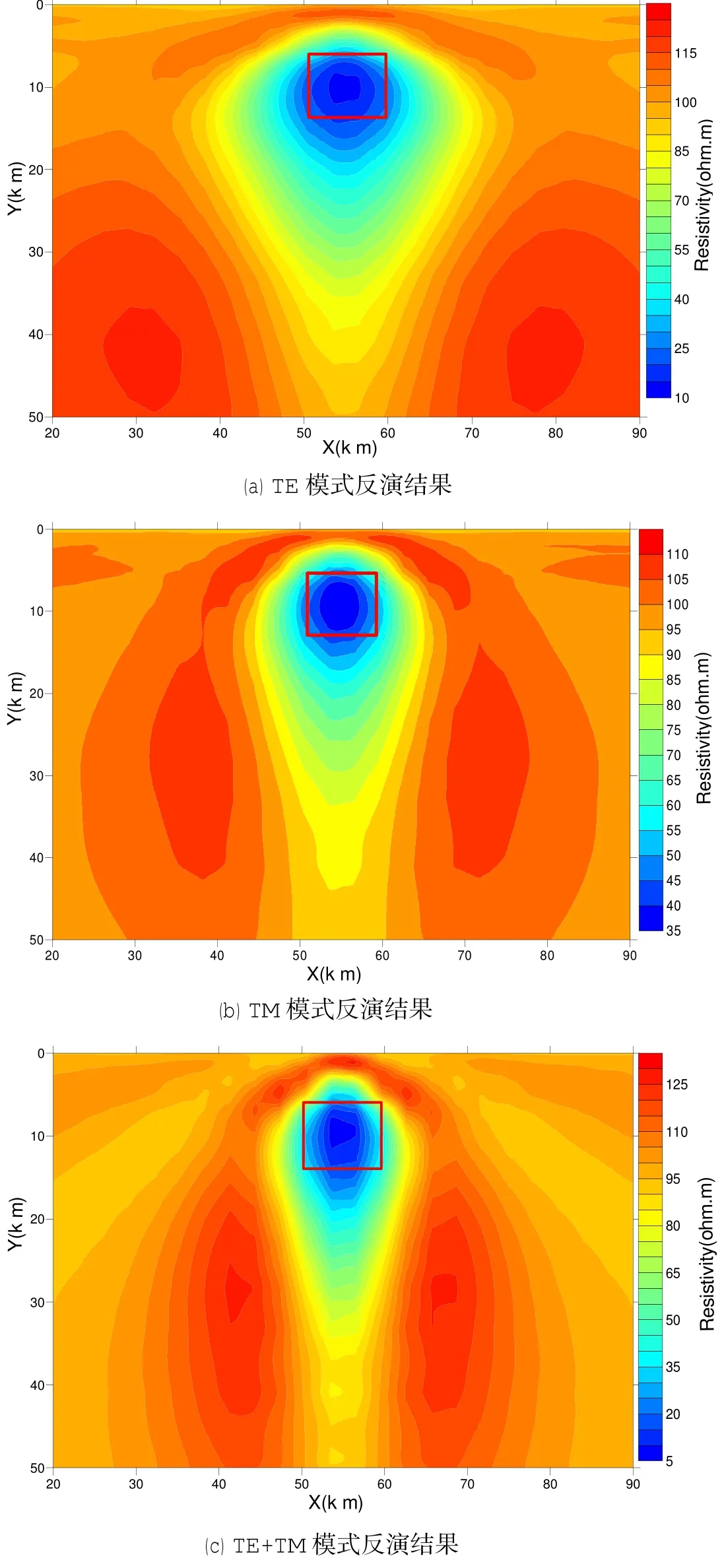
图2　不同模式低阻模型反演结果对比

保持其他设置仍不变，不同频点下反演效果如图4。从图中可以看出频点的选择在达到期望拟合差的前提下对反演效果的影响不大，同样能很好的突出异常体的位置及大小，背景电阻值也与预期值相近。频点的选择只会对反演计算的耗时有影响，频点选取越少计算越快，反演所用时间越少，反演达到期望拟合差用时越少。

图3　TE模式下不同测点数低阻模型反演结果对比

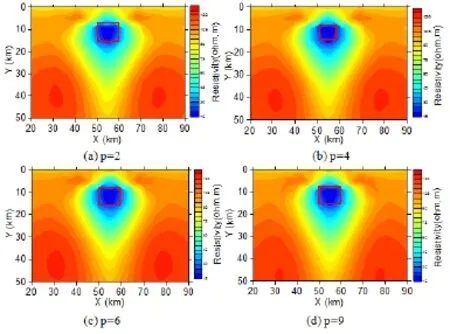
图4　TE模式下不同频点数低阻模型反演结果对比

3　结语

通过对单个低阻异常体的正反演研究得出以下结论：使用REBOCC方法进行大地电磁正反演都能达到预期的效果，视电阻率正演响应模型比相位模型能很好体现异常体的位置，同时TE模式的反演结果比TM模式更能清楚地反映异常体的特征；在反演过程中组合模式反演比单个模式反演效果更好，更能体现出异常体的形态及位置，组合模式反演受围岩影响最小，数据子空间的选择不同对反演效果影响不大，只是在反演过程耗时不同，频点越少，测点越小达到期望拟合差用时最少。

[1]Constable S C et al.Occam's inversion to generate smooth,two-dimensional models from magnetotelluric data[J].Geophysics,1990,55(12):1613-1624.

[2]Smith J T and Booker J R.Rapid inversion of twoand threedimensionalmagnetotelluricdata [J].J.Geophys.Res.,1991,96:3905-3922.

[3]Rodi W L and Mackie R L.Nonlinear conj-ugate gradient s algorithm for 2D magnetitelluricinversion[J].Geophysics,2001,66(1):174-187.

[4]Siripunvaraporn W and Egbert G.An effici-ent data-subspace inversion method for2Dmagnetotelluricdata[J].Geophysics,2000,65(3):791-803.

[5]胡祖志.大地电磁拟三维反演研究 [D].中国地质大学硕士学位论文,2005,5.

[6]何俊飞.大地电磁二维反演方法对比 [J].勘探地球物理进展,2010,33(1):26-31.

[7]胡祖志,胡祥云等.大地电磁二维反演方法对比研究 [J].煤田地质与勘探,2005,33 (1):64-67.

P631.3[文献码]B

1000-405X（2016）-9-231-2

吴满（1989～），男，助工，研究方向为工程物探方面。江枭（1989～），男，硕士，研究方向为工程物探检测。