东北严寒地区农村住宅耦合环境设计研究

甄 蒙，孙 澄，贾永恒

(哈尔滨工业大学建筑学院，黑龙江 哈尔滨 150006)



东北严寒地区农村住宅耦合环境设计研究

甄 蒙，孙 澄，贾永恒

(哈尔滨工业大学建筑学院，黑龙江 哈尔滨 150006)

在实际气候环境中，农宅同时受到热环境、光环境等多环境因素的共同作用，这就需要考虑多环境因素之间的交互作用，实现各参数的综合优化，达到节能的目的。通过对寒地农宅热环境、光环境的实际调研和模拟分析，确定农宅光热耦合环境的影响因素，应用BP神经网络建构农宅采暖能耗及天然采光照度的预测模型，为建筑师及农村居民在设计建造农宅时同时掌握采暖季能耗及天然采光照度情况提供指导，从而提高室内环境品质，降低农宅能耗水平。

东北严寒地区；农村住宅；耦合环境；BP神经网络

引言

在实际气候环境中，农宅往往同时受到热环境、光环境等多环境因素的共同作用，单一考虑某一环境因素不能满足农宅对于多环境要素的需求，这就需要综合考虑多环境要素的促进作用与制约关系，确定耦合作用下的环境参数优化设计区间，提出多环境耦合设计策略，从而提高室内天然采光照度，降低农宅能耗水平。

国内外学者对耦合节能设计进行了广泛的研究。从研究视角来看，Hien W N等学者从自然通风和建筑遮阳的角度对热带地区的办公建筑、住宅建筑的节能和热舒适进行了实际测试和模拟分析[1-7]，Ahlawat A S等人从耦合优化设计的角度研究了如何降低建筑的整体费用特别是能耗费用[8]，Zhai Z J等学者应用ES和CFD对不同耦合环境下的建筑能耗和通风进行了联合模拟，该研究能够预测建筑制冷能耗[9]。从应用ANN研究方法来看，Jian Y等学者应用ANN对中国不同气候区的建筑能耗进行了预测研究[10]，Ahmad A S等学者对应用SVM和ANN进行建筑电力能耗预测的文章进行了综述[11]，Turhan C等学者应用KEP-IYTE-ESS和ANN对建筑热负荷进行了对比研究[12]，Neto A H等学者应用EnergyPlus和ANN对建筑能耗预测进行了对比研究[13]，Kalogirou S A等学者应用ANN对被动式太阳能建筑能耗进行了预测，其多重确定系数为0.9991，预测速率与准确率均高于动态模拟程序[14]，Kalogirou S A等学者还对ANN在可再生能源系统的应用进行了文献综述[15]。

本文在前人的研究基础上，应用ANN对热环境和光环境共同作用下的寒地农宅热负荷及天然采光照度进行了研究。

1 研究方法

人工神经网络的概念来源于生物学启示，人脑由约1011个高度互联的单元组成，每个单元约有104个连接，这些单元被称为神经元，主要由树突、细胞体、轴突三部分组成(如图1所示)。人工神经网络(artificial neural network)是一种模仿生物神经网络的结构和功能的数学模型或计算模型。神经网络由大量的人工神经元联结进行计算。大多数情况下人工神经网络能在外界信息的基础上改变内部结构，是一种自适应系统。现代神经网络是一种非线性统计性数据建模工具，常用来对输入和输出间复杂的关系进行建模，或用来探索数据的模式[16]。人工神经网络的信息传递一般为多输入、单输出的非线性模式，通用的结构模型如图2所示。

人工神经网络是由大量的神经元互联而构成的网络。根据网络中神经元的互联方式，常见网络结构主要可以分为前馈神经网络(Feedforward Neural Networks)、反馈神经网络(Feedback Neural Networks)和自组织网络(Self-Organizing Neural Networks)3类。BP(Back Propagation)网络是1986年由Rumelhart和McCelland为首的科学家小组提出，是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。BP网络能学习和存储大量的输入/输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层(input)、隐藏层(hide layer)和输出层(output layer)。BP神经网络与其他神经网络模型的不同点是BP神经元的传输函数为非线性函数(感知机中为阶跃函数，在线性神经网络中为线性函数)，最常用的是log-sigmoid函数或tan-sigmoid函数(如图3所示)。BP神经网络一般为多层神经网络，隐层可以有多层，输出层的传输函数为线性函数或非线性函数，其中线性函数的输出结果取值范围较大，非线性函数取值范围较小，如logsig函数输出取值在(0,1)区间。

图1 生物神经元简图[17]Fig.1 Biological neurons diagram

图2 人工神经元示意图[18]Fig.2 Artificial neuron diagram

图3 典型的BP神经网络模型[19]Fig.3 The structure chart of typical neural network

本文以农宅采暖季热负荷及天然采光照度调研数据和模拟数据为基础，以SPSS17.0为软件平台，应用多层感知器(MLP)建立能耗及天然采光照度BP神经网络预测模型。

2 研究过程

2.1 数据预处理

神经网络的数据预处理对网络质量有着重要的作用，它直接影响网络的学习速度和精度。本节数据预处理包括输入数据、输出数据和抽取训练样本三部分。

2.1.1 输入数据预处理

将热环境的影响因素与光环境的影响因素进行分类整理，筛选光热耦合环境下的影响因素(如表1所示)。

表1 耦合环境影响因素研究表Table 1 Influence factors of coupling environment

由表1可以看出，影响光热环境的因素有很多，在以上16种因素中可以对部分因素进行合并处理。气候子区与光气候区合并，以城市名称表达；体形系数可以和房间长宽比、房间室内净高合并，以体形系数表达。因此，耦合环境输入因子确定为7项因素，分别为城市名称、体形系数、窗墙面积比、非透明围护结构传热系数、透明围护结构传热系数、非透明围护结构吸收系数、窗户总透射比。

原始数据样本不能直接用于神经网络训练，而是需要对原始数据进行归一化处理。原因是当输入变量很大时，训练函数的斜率会趋近0，这导致在训练神经网络过程中会出现梯度下降，当梯度有微小变化时，权值会相应变化，导致权值远离期望值。因此，归一化能够提高神经网络的训练效率。归一化的数据区间一般为(0，1)或(-1，1)，本次神经网络模型的输入样本和检验样本数据均统一量化为(0，1)。

数据归一化的处理方式为

(1)

(2)

式中xi为归一化后神经网络的输入值；xdi为原始输入值；xdmin为原始输入值中的最小值；xdmax为原始输入值中的最大值；ti为归一化后神经网络的目标值；ydi为原始目标值；ydmin为原始目标值中的最小值；ydmax为原始目标值中的最大值。

神经网络训练后，预测值为oi，取值范围为(0，1)，因此需要把预测值还原为实际值，即

(3)

式中ypi为预测值的还原值；oi为神经网络的预测输出值。

2.1.2 输出数据预处理

为便于神经网络计算，将输出数据转化为0和1组合的名义变量，即将输出数据变哑。根据预测目标，将采暖季热负荷数据分为“节能”和“不节能”两组，将天然采光照度数据分为“达标”和“不达标”两组(如表2所示)。

表2 原变量与哑变量对照表Table 2 The comparison of original variables and dumb variables

2.1.3 训练样本抽取

选取合适的训练样本能够提高神经网络的预测准确率。以寒地农村住宅天然采光照度为例，整体样本为200组数据，分别以训练样本占总体样本的50%，60%，70%，75%，80%为例进行对比研究，迭代次数设定为300次，每组重复训练10次，从而得到模型的平均预测准确率(如表3所示)。从表3可以看出，当训练样本比例为70%时，模型平均预测准确率最高，且预测稳定性良好。因此，选取70%的样本作为训练样本。

表3 不同训练样本比例的预测模型准确率Table 3 The prediction model accuracy of different percentage of training samples

2.2 参数设置

合理的参数设置能够提高神经网络的预测精度，对BP神经网络的迭代次数、隐藏层和函数选择进行对比研究。

2.2.1 迭代次数

迭代次数是指BP网络的运算次数。增大迭代次数可以减小网络训练误差，但是会相应的延长网络训练时间，因此，合适的迭代次数对网络是非常重要的。为寻求最优的迭代次数，以寒地农村住宅天然采光照度为例，训练样本设定为70%，迭代次数分别设定为100、300、500、1 000、2 000、5 000次为例进行对比计算(如表4所示)。从表4可以看出，当迭代次数为1 000次时，模型平均预测准确率最高，为80.82%。因此，模型迭代次数选用1 000次。

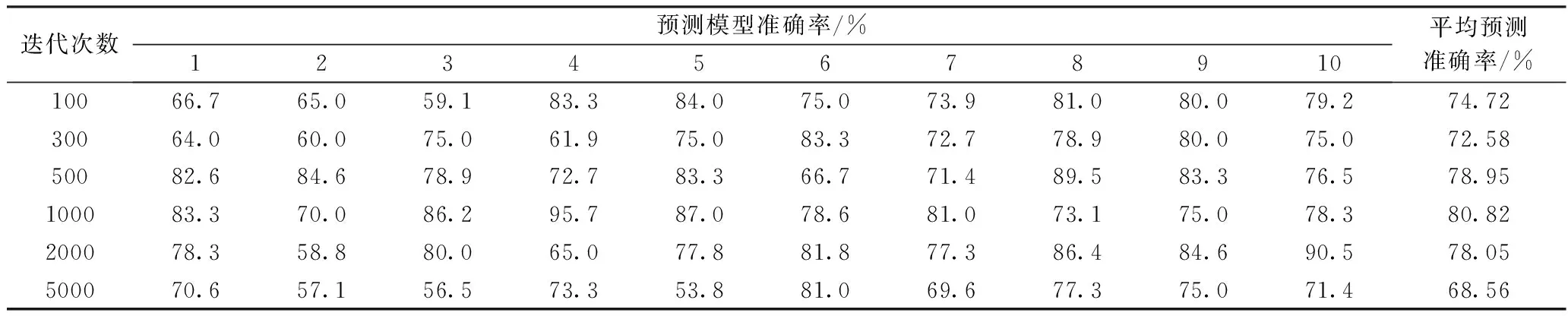
表4 不同迭代次数下的预测模型准确率Table 4 The prediction model accuracy of different iteration times

2.2.2 隐藏层

隐藏层及其节点数的设计是神经网络参数设置中重要而复杂的问题，其确定的基本原则是在保证模型预测精度的前提下，尽可能减少隐藏层节点数，从而使模型结构紧凑。根据前人的研究成果，隐藏层设定为1层或2层就可以解决各类问题。目前，科研人员均通过多次实验来确定隐藏层及其节点数的数量。采用对比实验的方式，以天然采光照度为例确定最佳隐藏层数量及节点数。

当设定一个隐藏层时，节点数分别设定为5、6、7、8、9、10、15、20、25、30、35、40，每个模型计算10次，取平均值比较模型预测准确率(如表5所示)。由表5可以看出，当节点数为7时，模型平均预测准确率取得最高值82.88%。当节点数进一步增大时，模型准确率开始下降，从8个节点到40个节点，模型预测准确率保持在70%～80%之间，这说明随着节点数的增大，模型预测准确率并没有随之提高。因此，以预测模型结构紧凑为原则，当采用一个隐藏层时，设置7个节点，模型预测效果最好。

当设定两个隐藏层时，节点数分别设定为10、15、25、35，同样每个模型计算10次，取平均值比较模型预测准确率。从表5可以看出，同样的10个节点，2个隐藏层预测准确率为72.67%，1个隐藏层预测准确率为71.19%，2个隐藏层比1个隐藏层准确率高1.48%。当节点数为15时，2个隐藏层预测准确率低于1个隐藏层7.08%，当节点数为25、35时，2个隐藏层预测准确率分别比1个隐藏层高1.41%和2.92%。总体来说，当节点数相同时，2个隐藏层的预测准确率略高于1个隐藏层。在2个隐藏层的设置中，当节点数为25时，预测准确率最高，为78.5%。

比较1个隐藏层和2个隐藏层的预测准确率可以发现，2个隐藏层使模型结构更为复杂，而且并没有显著提高预测效果，因此，选择1个隐藏层，7个节点的模型来进行预测。

表5 不同隐藏层个数及节点数下的预测模型准确率Table 5 The prediction model accuracy of different hidden layers and notes

2.2.3 函数选择

多层感知器是典型的前馈型神经网络结构，当采用BP算法时，即可实现BP神经网络预测。因此，在参数的设定中，隐藏层激励函数选择Sigmoid函数以实现BP神经网络。Sigmoid函数是典型的S型函数，其数学表达式为

(4)

其取实数值参数并将其变换到(0，1)范围。

2.3 模型检验

上文对输入数据、输出数据进行了预处理，并通过对比实验确定了最优样本训的抽取比例，即训练样本70%，检验样本20%，支持样本10%。同时，设定了模型的基本参数，即迭代次数1 000次，1个隐藏层，7个隐藏节点。以寒地农村住宅天然采光照度为例检验模型的预测准确度和稳定性。由表6可以看出，在进行的10次准确率计算中，预测准确率均在75%以上，这说明模型稳定性良好；并且平均准确率为83.51%，这说明预测准确性较好。

表6 寒地农村住宅天然采光照度预测模型Table 6 Prediction model for natural light illuminance in heating season

表6中A为城市；B为体形系数；C为窗墙面积比；D为非透明围护结构传热系数；E为透明围护结构传热系数；F为非透明围护结构吸收系数；G为窗户总透射比。

2.4 基于BP神经网络的耦合环境预测模型

本节应用BP神经网络建立东北严寒地区农村住宅热环境、光环境的耦合环境预测模型，模型包括通用模型和独立模型。

2.4.1 通用模型

选取哈尔滨、长春、沈阳、海拉尔四个城市分别代表黑龙江省、吉林省、辽宁省和内蒙古自治区东北部，及严寒(A)区、严寒(B)区和严寒(C)区三个子气候区。其中哈尔滨属严寒(B)区，长春、沈阳属严寒(C)区，海拉尔属严寒(A)区。以调研及模拟数据为基础建立通用模型(见表7)。由表7可以看出，采暖季热负荷平均预测准确率为78.71%，天然采光照度平均预测准确率为93.03%。从数据可以看出，通用模型具有较高的预测精度。建筑师在设计农宅时可根据此模型对寒地农宅采暖季能耗、天然采光照度进行预测，并对模型进行节能优化，也可对已建成农宅进行节能评价及改造。

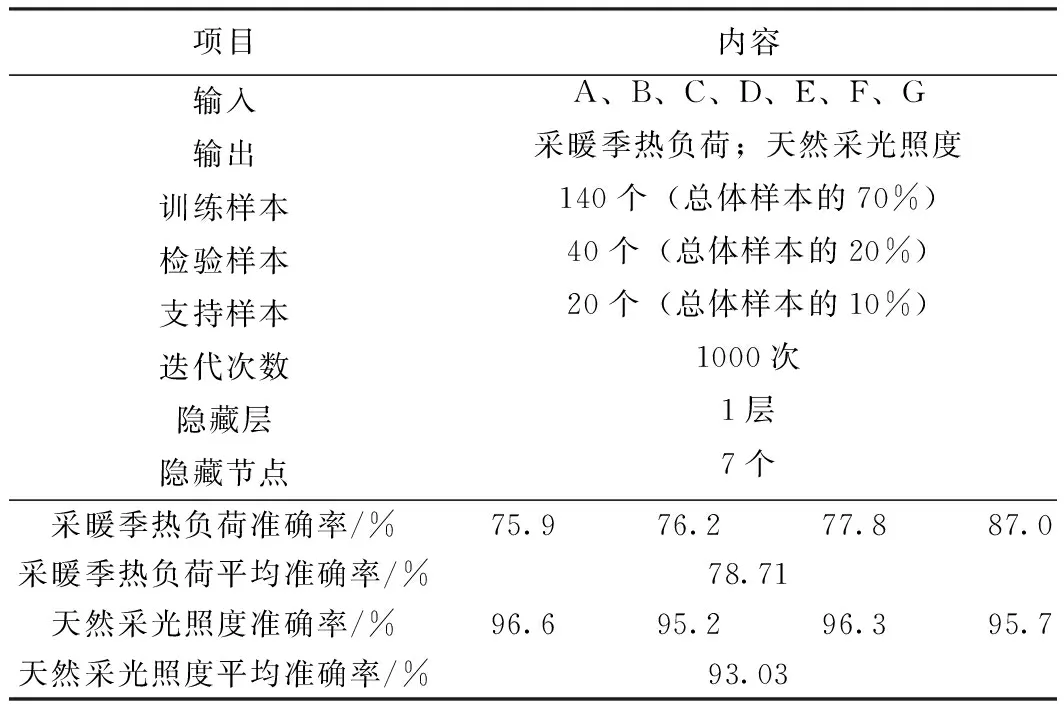
表7 耦合环境预测的通用模型Table 7 Generalized model for predicting the coupling environment

表7中A为城市；B为体形系数；C为窗墙面积比；D为非透明围护结构传热系数；E为透明围护结构传热系数；F为非透明围护结构吸收系数；G为窗户总透射比。

通过通用模型网络图表(如图4所示)可以看到BP神经网络的三层结构，并且能够看到键结值的连接关系。键结值能够反映给定层中的单位与下层中的单位之间关系的系数估计值。图中蓝线键结值小于0，灰线键结值大于0。

每种自变量对输出结果的影响程度不同，因此根据其对输出结果的影响程度进行重要性排序(如表8、图5所示)。由表8及图5可以看出，窗户总透射比的重要性最大，其标准化的重要性为100%；其次为非透明围护结构传热系数，其标准化的重要性为71.6%；第三为窗墙面积比，其标准化的重要性为59.9%；城市、透明围护结构传热系数、非透明围护结构吸收系数和体形系数的影响程度较为接近，分别为23.3%，22.9%，21.4%和18.2%。因此，建筑师及农村居民在设计建造农宅时可根据自变量的重要性进行节能设计。

表8 自变量重要性Table 8 Significance of independent variable

2.4.2 独立模型

为分别研究每个气候子区，每个城市的耦合环境，分别建立了哈尔滨、长春、沈阳、海拉尔的耦合环境独立模型(如表9所示)。由表9可以看出，哈尔滨、长春、沈阳、海拉尔四个城市的采暖季热负荷平均预测准确率均在70%以上，具有较好的预测效果，其预测准确率分别为76.76%、70%、72.14%和76.92%。四个城市的天然采光照度平均预测准确率均在75%以上，具有良好的预测效果，其预测准确率分别为77.02%、77%、78.07%和84.32%。该预测模型能够在一定程度上代表严寒(A)区、严寒(B)区和严寒(C)的情况，各气候子区的城市、农村可根据相应的独立模型进行预测。

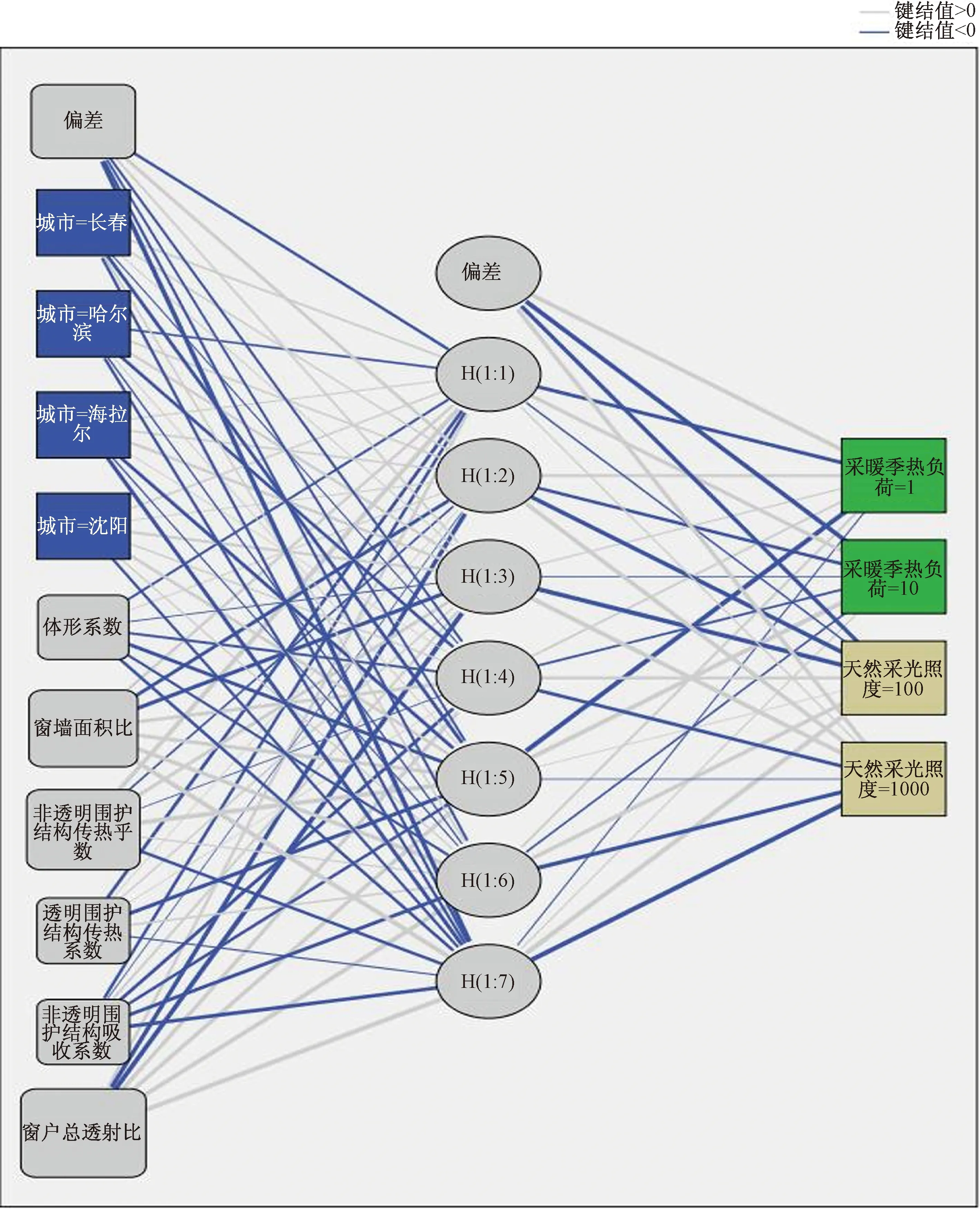
图4 通用模型网络图表Fig.4 Network diagram for generalized model

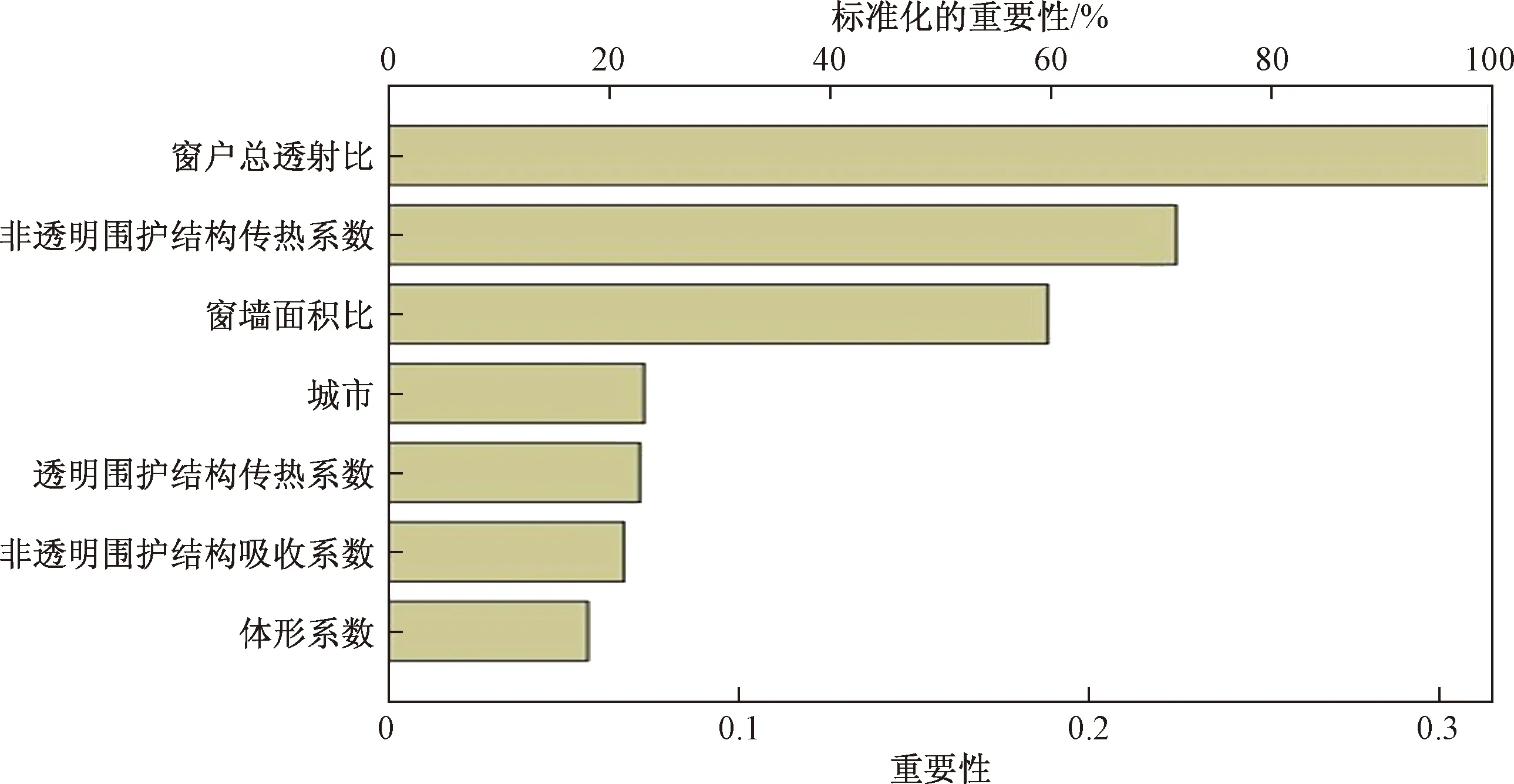
图5 自变量的重要性排序Fig.5 The importance order of input factors

项目内容气候子区严寒(B)区严寒(C)区严寒(C)区严寒(A)区地点哈尔滨长春沈阳海拉尔输入A、B、C、D、E、F、G输出采暖季热负荷;天然采光照度训练样本35个35个35个35个检验样本10个10个10个10个支持样本5个5个5个5个迭代次数1000次隐藏层1层隐藏节点7个采暖季热负荷准确率/%71.483.366.766.760.075.085.761.560.080.085.770.075.063.681.880.075.066.780.077.875.083.380.068.883.385.780.071.472.762.575.064.370.080.066.777.8采暖季热负荷平均准确率/%76.767072.1476.92天然采光照度准确率/%85.783.385.760.090.991.780.076.975.085.793.891.775.081.860.075.087.590.083.385.790.090.075.072.780.066.775.091.792.390.975.070.066.783.380.086.7天然采光照度平均准确率/%77.027778.0784.32

注：A——城市；B——体形系数；C——窗墙面积比；D——非透明围护结构传热系数；E——透明围护结构传热系数；F——非透明围护结构吸收系数；G——窗户总透射比。

3 天然采光实测验证

3.1 测试对象

课题组于2016年1月8日上午11:00分对寒地某农村住宅进行了天然采光实地测试，测试天气为晴天。住宅建成于2015年，南北向，双坡屋顶一层建筑，建筑高度5.7 m，室内净高3 m。课题组对每个房间进行了逐一测试，以检验其天然采光照度水平和预测模型准确度。

3.2 测试方法

根据《建筑采光设计标准》(GB 50033—2013)的要求，选择各个房间通过侧窗中心线的剖面布置测点，测点间距0.8 m(卫生间测点间距0.6 m)，测点高度0.75 m，每个测点读数三次，取平均值。测点距墙的间距为0.5 m，同时测试室外照度。测试仪器为Fluke941型数字式照度计，测量范围为20 lx～200 000 lx(如图6所示)。

图6 测点分布图Fig.6 Measure points distribution

3.3 测试结果

通过对农村住宅进行天然采光实地测试共得到40组，120个照度值。取每个测试点3个照度的平均值，得到主卧室、起居室等每个房间各测点的平均照度值和总照度平均值(见表10)。由测试结果

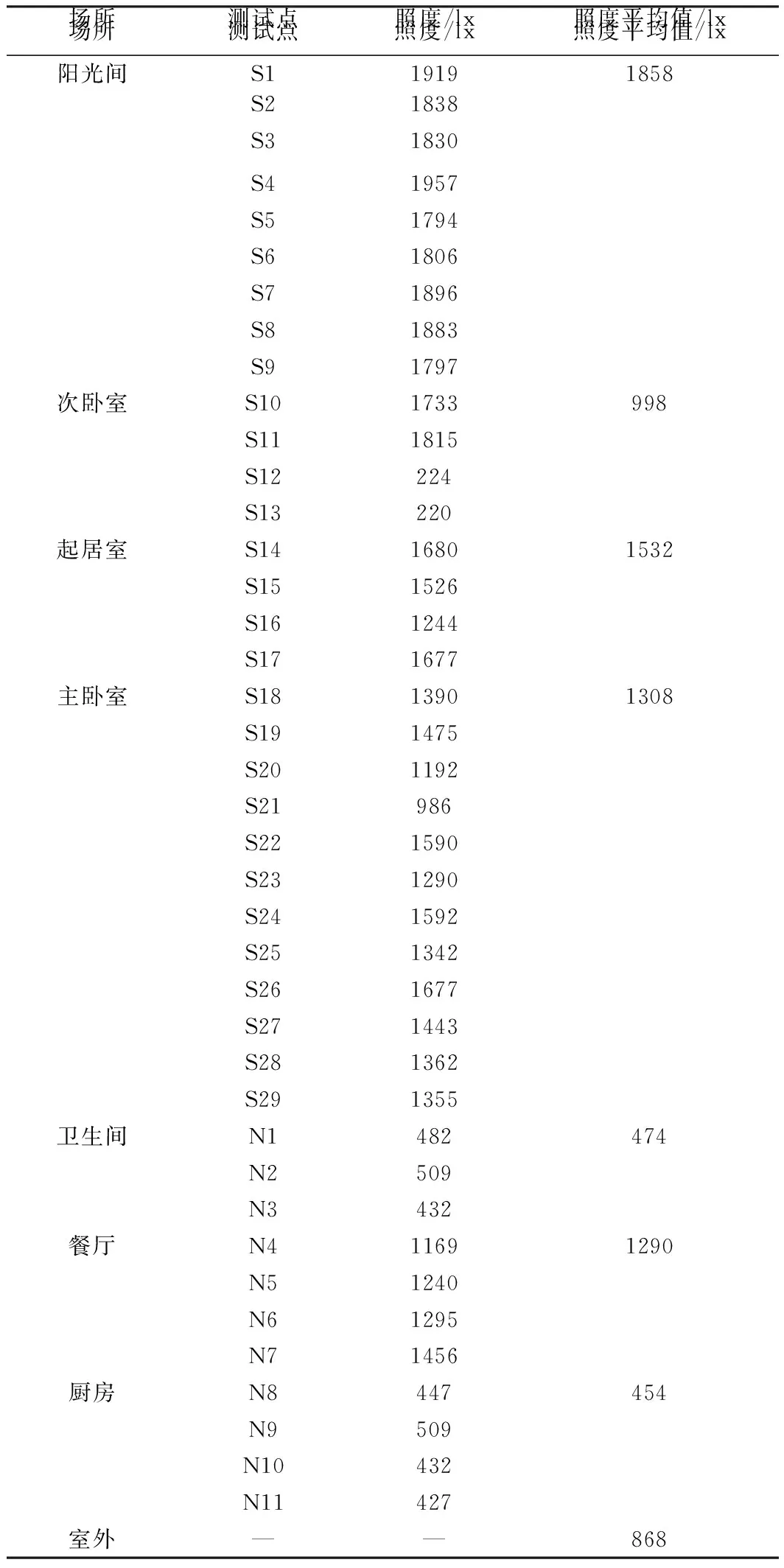
表10 节能住宅天然采光照度实测结果Table 10 The experimental result of rural energy-saving residential daylighting illuminance

可以看出阳光间平均照度为1 858 lx，次卧室平均照度为998 lx，起居室平均照度为1 532 lx，主卧室平均照度为1 308 lx，卫生间平均照度为474 lx，餐厅平均照度为1 290 lx，厨房平均照度为454 lx，均高于《建筑采光设计标准》(GB 50033—2013)规定的标准值300 lx。因此，该农村住宅的天然采光符合国家规范要求。

4 结论

本文应用BP神经网络对东北严寒地区农村住宅热环境、光环境多因素综合作用下的耦合设计进行了研究，得到如下主要结论：

1)综合考虑热环境、光环境对农宅的影响，最终确定了7项耦合环境设计因素，分别为：城市、体形系数、窗墙面积比、非透明围护结构传热系数、透明围护结构传热系数、非透明围护结构吸收系数、窗户总透射比。

2)应用BP神经网络，以实际调研数据及模拟数据为基础建立了寒地农宅采暖季热负荷及天然采光照度的预测模型，该模型包括通用模型和独立模型。模型具有较高的预测精度，通用模型预测精度为能耗78.71%，照度93.03%。独立模型预测精度为：哈尔滨能耗76.76%、照度77.02%；长春能耗70.00%、照度77.00%；沈阳能耗72.14%、照度78.07%，海拉尔能耗76.92%、照度84.32%。建筑师可根据预测模型对东北严寒地区的农宅进行节能设计、节能评价及节能改造。

3)根据预测结果，影响农宅采暖热负荷及天然采光照度自变量的重要性排序为：窗户总透射比(100%)，非透明围护结构传热系数(71.6%)，窗墙面积比(59.9%)，城市(23.3%)，透明围护结构传热系数(22.9%)，非透明围护结构吸收系数(21.4%)，体形系数(18.2%)。

[1] HIEN W N, LIPING W, Chandra A N, et al. Effects of double glazed facade on energy consumption, thermal comfort and condensation for a typical office building in Singapore[J]. Energy and Buildings, 2005, 37(6): 563-572.

[2] LI Ping W, HIEN W N. The impacts of ventilation strategies and facade on indoor thermal environment for naturally ventilated residential buildings in Singapore[J]. Building and Environment, 2007, 42(12): 4006-4015.

[3] WANG L, WONG N H. Coupled simulations for naturally ventilated rooms between building simulation (BS) and computational fluid dynamics (CFD) for better prediction of indoor thermal environment[J]. Building and Environment, 2009, 44(1): 95-112.

[4] LI Ping W, HIEN W N. Applying natural ventilation for thermal comfort in residential buildings in Singapore[J]. Architectural Science Review, 2007, 50(3): 224-233.

[5] WANG L, WONG N H. Coupled simulations for naturally ventilated residential buildings[J]. Automation in Construction, 2008, 17(4): 386-398.

[6] ZHANG R, LAM K P, Yao S C, et al. Coupled EnergyPlus and computational fluid dynamics natural ventilation simulation[C]//Proceedings of 5th National SimBuild Conference. 2012.

[7] LI Ping W, HIEN W N. Natural ventilation simulation with coupling program between building simulation (BS) and computational fluid dynamics (CFD) simulation program for accurate prediction of indoor thermal environment[J].

[8] AHIAWAT A S, RAMASWAMY A. Coupled Optimal Design of Building with TMD[J]. XXI ICTAM, Warsaw, Poland, 2004.

[9] ZHAI Z J, CHEN Q Y. Performance of coupled building energy and CFD simulations[J]. Energy and buildings, 2005, 37(4): 333-344.

[10] CHENG-wen Y, JIAN Y. Application of ANN for the prediction of building energy consumption at different climate zones with HDD and CDD[C]//Future Computer and Communication (ICFCC), 2010 2nd International Conference on. IEEE, 2010, 3:286-289.

[11] AHMAD A S, HASSAN M Y, ABDULLAH M P, et al. A review on applications of ANN and SVM for building electrical energy consumption forecasting[J]. Renewable and Sustainable Energy Reviews, 2014, 33: 102-109.

[12] TURHAN C, KAZANASMAZ T, UYGUN I E, et al. Comparative study of a building energy performance software (KEP-IYTE-ESS) and ANN-based building heat load estimation[J]. Energy and Buildings, 2014, 85: 115-125.

[13] NETO A H, FIORELLI F A S. Comparison between detailed model simulation and artificial neural network for forecasting building energy consumption[J]. Energy and Buildings, 2008, 40(12): 2169-2176.

[14] KALOGIROU S A, BOJIC M. Artificial neural networks for the prediction of the energy consumption of a passive solar building[J]. Energy, 2000, 25(5): 479-491.

[15] KALOGIROU S A. Artificial neural networks in renewable energy systems applications: a review[J]. Renewable and sustainable energy reviews, 2001, 5(4): 373-401.

[16] http://zh.wikipedia.org/wiki/%E4%BA%BA%E5%B7%A5%E7%A5.

[17] http://www.aiseminar.cn/bbs/forum.php?mod=viewthread&tid=924.

[18] http://zh.wikipedia.org/wiki/File:Ncell.png.

[19] http://ibillxia.github.io/blog/2013/03/30/back-propagation-neural-networks/.

Study on Coupled Environment Design of Rural Residential Buildings in Severe Cold Regions of Northeast China

ZHEN Meng, SUN Cheng, JIA Yongheng

(SchoolofArchitecture,HarbinInstituteofTechnology，Haerbin150006,China)

In the actual climatic conditions, rural residential buildings were affected by thermal environment, natural lighting environment, and etc. It requires consideration of the interaction among environmental factors to achieve integrated optimization of the parameters and to achieve energy efficiency. The paper selects the influencing factors through field survey and simulation analysis. The paper constructs the prediction model of energy consumption in heating season and natural lighting illuminance of rural residential buildings using BP neural network. The model can provide guidance for architects and rural residents when they design and build rural residential buildings. Thereby, the model can improve indoor environmental quality and reduce energy consumption of rural residential buildings.

severe cold regions of northeast; rural residential building; coupled environment; BP neural network

黑龙江省经济社会发展重点研究课题(编号：15030)，“十二五”国家科技支撑计划课题资助项目(编号：2013BAJ12B04)

TM923

A

10.3969j.issn.1004-440X.2016.04.020