多学科优化方法在船舶结构设计中的应用

张超群， 阎 岩， 金允龙， 姜河蓉

(上海船舶运输科学研究所 航运技术与安全国家重点实验室，上海 200135)



多学科优化方法在船舶结构设计中的应用

张超群， 阎 岩， 金允龙， 姜河蓉

(上海船舶运输科学研究所 航运技术与安全国家重点实验室，上海 200135)

在多学科优化设计方法的基本理论框架下，集成有限元建模和分析软件进行结构优化技术的研究。以某67 000 DWT新巴拿马型散货船的货舱段为研究对象，利用多学科优化软件集成有限元软件patran和nastran,以板材厚度作为设计变量，以最大许用应力作为约束条件，以舱段结构重量作为目标函数，选取自适应模拟退火算法进行结构优化计算。对该优化结果进行屈曲校核分析结果表明,优化后较大地减少了舱结构重量,屈曲强度满足规范要求。

多学科优化；货舱段；有限元；模拟退火

0 引 言

由船舶能效设计指数(Energy Efficiency Design Index,EEDI)计算公式可知，在船舶主尺度确定的前提下，载重量提高就意味着能效水平提高，想要提高船舶载重量就必须降低空船重量。因此,减少空船重量不仅可以降低建造成本,而且能提高船舶能效水平。

图1 优化流程图

对船舶结构进行优化设计可减少空船重量，而传统的船舶优化设计主要依据经验和规范，按照螺旋线前进，采用的串行设计流程割裂了学科间的耦合[1]。同时,这种设计只是局部的优化设计，并不是真正的全局最优设计。船舶设计涉及到快速性、耐波性、操纵性、总布置、结构强度和经济性等众多独立学科[2]，是典型的多学科设计优化问题;而通常精度较低的经验公式计算已无法满足实际工程需要。对此，这里主要研究在多学科设计优化模型中集成有限元软件进行船舶舱段结构优化设计。优化设计的主要流程见图1。

1 有限元计算模型

1.1 模型范围

以一艘67 000 DWT新巴拿马型散货船为研究对象。其舯部货舱区域结构的重量约占整个船体结构重量的70%，是船体最主要的结构，决定了船舶最终的结构重量和建造费用。因此,船舶结构优化设计的首要目标就是对船体货舱区域结构进行优化设计。

所取的模型范围为舯部货舱区域“1/2货舱+1个货舱+1/2货舱”，即从FR89肋位到FR165肋位，涵盖散货船3号货舱及2号和4号货舱的1/2(见图2)。

燃油舱、淡水舱和压载舱的重量及其对舱壁的作用利用多点约束(Multi-point Constraint,MPC)来等效，空船重量与实船重量的差值通过增加重量点的方式调节[3]。有限元模型及有效分析区域模型见图2和图3。

图2 有限元模型

图3 有效分析区域

1.2 边界条件

根据《钢制海船入级规范》2015版第2分册，模型两端通过MPC独立点施加约束。MPC独立点的垂向位置一般取在横剖面中和轴高度处。前后端面的约束见表1。

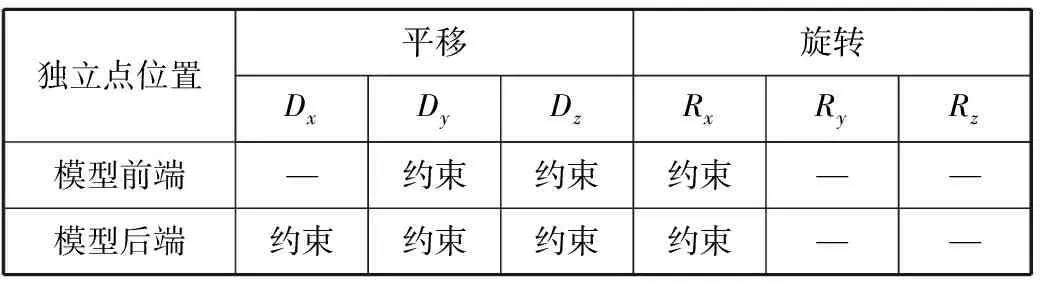
表1 前后端面约束

1.3 载荷工况

为简化计算，选择3种相对较危险的装载工况校核舱段受力情况。载荷包括静水载荷、波浪载荷和货物对舱壁的压力等(见表2)。

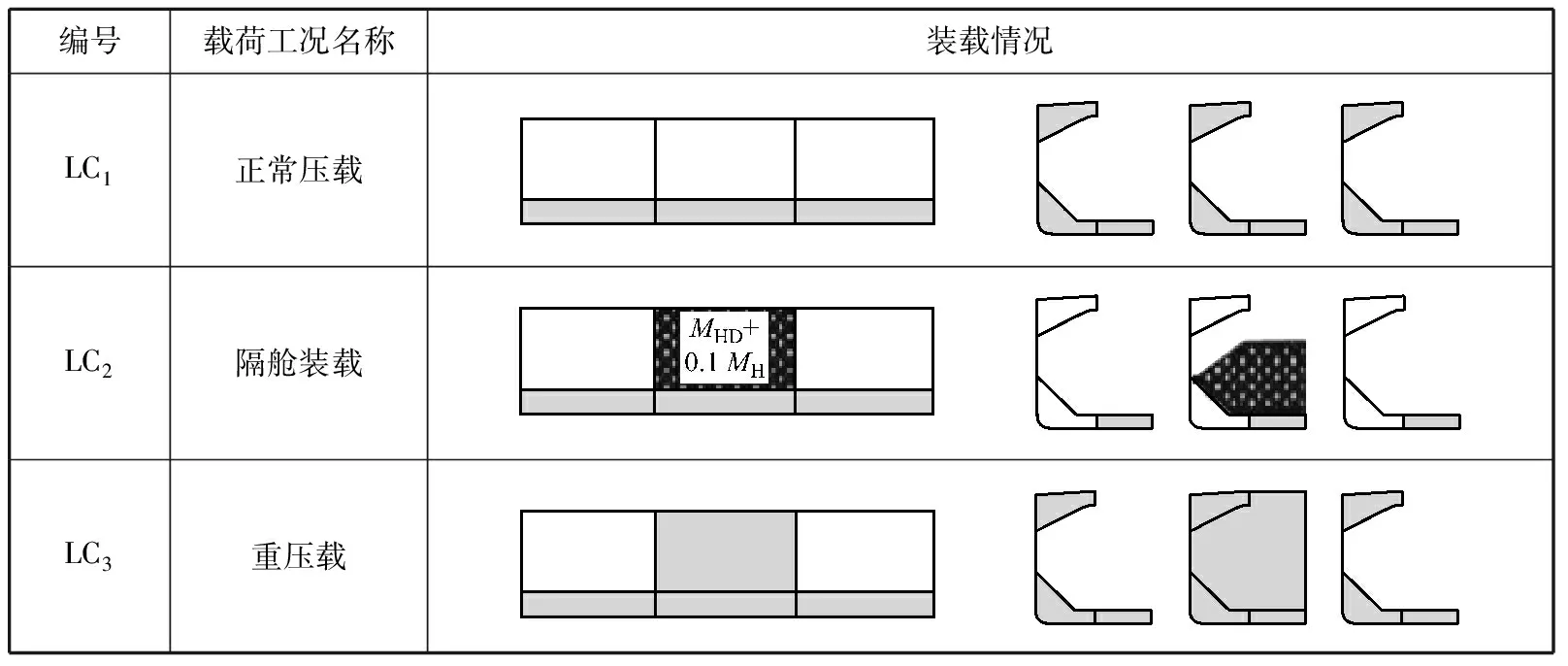
表2 典型计算工况

2 舱段优化模型

2.1 设计变量

在多学科优化设计中，船舶主尺度涉及到多个学科。由于这里仅对船舶结构进行优化设计，因此把主尺度作为确定值。船体采用普通钢,AH32级高强度钢和AH36级高强度钢建造。其中:货舱区域纵向构件主要采用AH36级高强度钢;横向构件采用AH32级高强度钢。因此,在货舱段对钢材型号进行优化的作用不大，将其作为确定值来研究。板材的宽度和焊缝不变，也作为确定值直接在原图上量取。

由于有限元软件对板单元的应力分析更真实可信，因此只选取板单元作为设计参数。货舱分析区域共选取37个变量，加强肘板和横向强框架没有参与优化。对于各板单元的厚度，考虑到实际情况，为简化优化过程、减少计算时间及提高优化设计效率，在满足规范计算最小厚度的前提下选取离散设计变量。优化设计变量及其取值范围见表3。

2.2 约束条件

构件的参考应力不超出相应的屈服应力即认为满足许用应力标准,通常取Von Mises相当应力,即

(1)

式(1)中：σx和σy为单元正应力；τxy为单元剪应力。

根据《钢制海船入级建造规范》强度直接计算中屈服计算的有关规定来定义约束条件。若仅以钢材的屈服应力值作为约束条件，则很多板材的厚度将远远超过其最小值，未能得到合理优化，且不同货舱区域的钢材等级和材料系数均不同。因此，采取对不同板材设定不同的约束条件的方式(见表4)，使优化更合理[4]。

2.3 目标函数

(2)

式(2)中：X为设计变量；F(X)为目标函数；hj(X)为等式约束；gk(X)为不等式约束。

3 优化的实现

3.1 优化流程

3.1.1 前期准备

(1) 利用patran软件建立有限元模型，定义材料，附构件属性，加载相应载荷工况；

(2) 重新打开patran软件，修改模型中板单元的属性，进行强度校核，生成.bdf文件，关闭patran软件，得到patran.ses.01文件；

表3 优化设计变量及其取值范围

表4 应力约束

(3) 利用nastran对.bdf文件进行计算分析，得到.op2文件；

随着经济的发展，人民的思想观念发生了很大的变化，对于生活质量的要求在不断的提高，园林建设是城市中不可缺少的部分，人民对于其的重视程度较高，近些年我国园林绿化水平在不断的提高，彩色树种在园林绿化过程中发挥着重要作用，本文对彩色树种在园林绿化中的应用与作用进行深入研究。

(4) 用patran软件导入.op2文件，生成质量和应力报告.rpt文件，得到patran.ses.02文件。

3.1.2 集成过程

(1) 编写批处理文件，用多学科优化软件驱动patran软件，修改模型单元的属性，形成1个输入文件；

(2) 编写批处理文件，用多学科优化软件驱动nastran软件，在后台对新的模型进行应力分析；

(3) 编写批处理文件，用多学科优化软件再次驱动patran软件，输出模型重量和最大应力报告，形成输出文件；

(4) 用多学科优化平台将以上3个批处理文件集成起来，选取适当的优化算法，对变量设定取值范围，对最大应力设定约束条件，把最小重量作为优化目标，即可进行船舶结构优化设计。

3.2 优化算法

自适应模拟退火算法是20世纪90年代初Lester Ingber研究传统的模拟退火法和模拟淬火过程后提出的，是一种以固体退火过程的物理现象和统计物理学原理为背景，基于Monte Carlo迭代求解策略的随机寻优算法。该算法可用来解决具有多峰和非光滑性的高难度非线性优化问题[5]，在其搜索过程中能概率性地跳出局部最优解，最终收敛于全局最优解。该算法的优势在于参数较少、好控制，无需要求设计空间连续或凸性；其缺点是无法并行计算和费用高。

模拟退火算法用Metropolis准则产生组合优化问题解的序列，其求解最优值问题的步骤[6]为：

1) 在解空间内随机产生初始解s，设初始迭代次数i=0，并给定初始温度tk=maxT；同时，计算该状态下的目标函数值F(s)。

2) 判断是否满足内循环终止条件，即是否满足Metropolis抽样稳定性准则。若满足内循环终止条件，则转入步骤6)；否则，转入步骤3)。

3) 给当前解s,1个随机扰动，即在s的邻域内随机产生新解s′，计算该新解的目标函数值F(s′)。

4) 若F(s′)

5) 判断是否满足pr-ξ=exp[-(F(s′)-F(s))/ti]-ξ>0。若满足，则用扰动解替换当前解s，即s⟸s′，F(s)⟸F(s′),转入步骤2)。

6) 降温过程。令ti+1=update(ti)，并令i=i+1，判断是否满足外循环终止条件。若满足外循环终止条件，则当前解即为最优解s*，算法结束；否则,转向步骤3)。

3.3 优化结果

经过约300 h的计算，3种工况下分别得到较优值，此时从每个变量中选出最大值，即为满足这3种工况的最好结果，优化结果见表5。

在3种工况下，有效分析区域的应力云图(见图4～图6)。

图4 LC1构件应力图

图5 LC2构件应力图

图6 LC3构件应力图

3.4 屈曲强度校核

高强度钢的大量使用和船舶结构经过尺寸优化后板材厚度的减小最容易导致稳定性丧失，结构抵抗外载荷的最大承载能力受到影响[7]。因此,在对屈服强度进行优化后，要继续对优化后的结构屈曲强度进行校核分析。板格屈曲安全因子λ应不小于表6中的最小屈曲安全因子,校核结果都满足屈曲要求。3种工况中各构件处的最小屈曲安全因子见表6。

4 结 语

优化后的3号舱结构重量为1 904.66 t，相比优化前舱段结构重量1 982.39 t减少了3.88%。在满足应力水平要求的前提下，较大地减少了舱段结构的重量。对其进行屈曲校核，满足规范要求。

该优化流程中,基于直接计算的有限元优化模型，仅对板材的屈服计算进行了集成优化。若优化平台能集成专业性的分析软件，则可尝试用平台调用船舶专业软件，以板材的屈服、屈曲，甚至是疲劳强度作为约束条件进行尺寸优化。按照这样的方法可建立船舶多学科优化设计模型的结构优化模块，结合其他学科的精确计算，实现对船舶的多学科优化设计。

表5 优化结果

表6 最小屈曲安全因子

[1] 潘彬彬，崔维成. 基于有限元的整船结构多学科设计优化[J].中国造船，2010,51(1)：47-54.

[2] 刘克峰.船舶多学科设计优化建模研究[D].武汉：武汉理工大学，2010.

[3] 李冬琴，杨永祥，蒋志勇.一种多学科设计优化近似模型构建方法[J].中国造船，2011,52(3):59-66.

[4] 顾晔昕，詹志鹄，汤明文,等.集装箱船整船结构三维有限元强度分析方法研究[J].中国造船，2001,42(3)：15-21.

[5] 刘鹏,刘玉玲,余飞鸿.基于自适应模拟退火算法的薄膜特性参数计算方法研究[J].光学仪器，2005,27(4)：73-77.

[6] 秦洪德.船舶结构优化设计[M].哈尔滨：哈尔滨工程大学出版社，2011:85-86.

[7] DAS P K, THAVALINGAM A, BAI Y. Buckling and Ultimate Strength Criteria of Stiffened Shells Under Combined Loading for Reliability Analysis[J]. Thin-Walled Structures,2003,41(1):69-88.

Application of Multidisciplinary Optimization in Ship Structural Design

ZHANG Chaoqun, YAN Yan, JIN Yunlong, JIANG Herong

(StateKeyLaboratoryofNavigationandSafetyTechnology,ShanghaiShip&ShippingResearchInstitute,Shanghai200135,China)

The structural optimization is achieved by integrating FEM modeling and analysis tools into the multidisciplinary design optimization framework. The case illustrated is the process for the cargo section of a 67 000 DWT bulk. The FEN software, patran and nastran, are integrated with the multidisciplinary optimization software first. The variables in the model are defined as follows: the thickness of plates as the design parameters, the maximum allowable stress as the constraint condition and the compartment structure weight as the objective function. The problem is solved with Adaptive simulated annealing algorithm. Finally, the optimized results are checked with buckling calculation.

multidisciplinary optimization; cargo section; FEM; simulated annealing

2016-04-25

张超群(1990—)，男，江苏丹阳人，硕士，主要从事船舶与海洋工程结构物设计制造研究。

1674-5949(2016)03-0018-06

U661.42

A