GPU的对半剖分体数据的光线投射法

于 水，王宽全，夏 勇，张恒贵

(哈尔滨工业大学 计算机科学与技术学院，150001哈尔滨)



GPU的对半剖分体数据的光线投射法

于 水，王宽全，夏 勇，张恒贵

(哈尔滨工业大学 计算机科学与技术学院，150001哈尔滨)

为解决传统可视化方法无法有效跳过具有空腔结构数据集的中空体素的问题，提出一种基于GPU的面向中空结构体数据的光线投射法.在进行光线投射之前，首先把体数据对半剖分成两部分，对此两部分分别使用八叉树进行重构，并同时剔除空块，建立起各自新的有效数据块的顶点集合；然后使用GPU对顶点集合进行渲染，生成光线起点和方向等信息；最后利用CUDA对重构后的两部分体数据依次进行光线投射和颜色累积，将其结果合成后得到最终图像.实验结果表明，这种方法生成的图像质量与传统的可视化方法相比没有损失，但对具有较多空腔结构的体数据，则可以快速跳过中空体素，具有非常明显的加速效果.

数据可视化；光线投射法；GPU渲染；八叉树；CUDA ；中空体数据

光线投射法是一种直接体绘制算法，最先由Levoy[1]提出，可以生成高质量的3D图像.早期的光线投射法大都在CPU上实现，因其运算量大，导致绘制速度慢，难以满足实时性要求.近年来随着GPU硬件的发展，基于GPU的并行图形可视化技术得到迅猛发展，光线投射法的计算量瓶颈问题也得到极大的缓解.文献[2]首次提出了基于GPU三线性插值能力的三维纹理体绘制方法.随后，Cabral等[3]对此方法进行了改进，通过三维纹理映射实现了交互式体绘制，从而使基于纹理映射的方法一段时间内成为最常用的交互式体绘制方法.然而这种方法仍然存在一些很难解决的问题：在三维体数据中，通常只有5%～40%的数据是有意义或可见的，在体绘制过程中，会产生大量的对最终图像没有贡献的切片，但是在计算过程中对这些切片仍然需要进行采样、数值计算，大大影响了绘制时间.Westermann等[4]将体数据看作三维包围盒(bounding box)，通过光线与包围盒的求交运算，得到每条光线与包围盒的交点，并在GPU上实现了并行光线投射法，大大提高了图像质量.Hadwiger等[5-6]进一步通过结合GPU渲染和数据分块算法如KD树[7]、八叉树[8-9]等，实现快速剔除有效体数据与包围盒边界之间的空体素，在保证图像质量的前提下，极大提高了绘制速度，现已成为在GPU上常用的光线投射方法.但这种方法对于具有较多中空结构的体数据则依然无能为力，仍然浪费了大量的空体素计算时间，影响可视化速度.

康健超等[10]使用基于八叉树编码的方法，将原始数据剔除空体素后重新写入三维纹理中，最后使用CUDA实现光线投射，提升了绘制效率，但这种方法只是简化了部分颜色累积运算，并没有真正跳过空体素.自适应采样频率方法[11-12]可以部分解决中空结构体数据的空体素跳过问题，但这种方法需要对体数据进行统计学预计算，如对体数据通过FFT变换进行频谱分析等，这个过程的计算量非常大，且由于不同的自适应采样规则采样频率不同，对图像质量的影响也比较明显.叶良等[13]通过二级可变步长的方法来解决对于中空结构数据的空体素跳过问题，但是这种方法依然不够灵活，对于较大的中空结构，也仍然需要多次重复跳过，增加了算法运行时间.

目前针对具有较多中空体素的体数据的可视化问题，鲜有文献专门提出此类解决方法.本文在Westermann方法和八叉树剖分方法的基础上，提出一种基于GPU的面向空腔结构数据集的光线投射法.其主要特点是在使用GPU进行渲染之前，先把体数据剖分成两部分后利用八叉树进行重构，再分别对重构后的两部分进行光线投射和颜色累积，最后将结果进行合成，得到最终图像.实验结果表明本文方法对于中空结构的体数据，具有非常明显的加速作用.

1 基于GPU的光线投射法

1.1 光线投射法

光线投射法是指从图像的每一个像素，沿视线方向发射一条光线，光线穿越整个图像序列，并在这个过程中，对图像序列进行采样获取颜色信息，同时依据光线吸收模型将颜色值进行累加，直至光线穿越整个图像序列，最后得到的颜色值就是渲染图像的颜色.如图1所示，是一条典型的光线投射过程.

图1 光线投射过程

在发射-吸收模型的光线投射法中，图1在t=d处，由于通常体素对光线的吸收率不为常量，而是随着位置变化而发生变化，因此在t=d处的颜色值计算公式为

式中：c′为由于存在对光线的吸收因素而最终发出的光线颜色;c为体素本来的光线颜色;k为光线吸收率，且为一个常量;d为体素与视点间的距离.

提取吸收率的积分公式为

上式也叫光学深度(optical depth)，基于一个点的计算方法，如果要计算沿光线所有点最终进入人眼的颜色值，就要将所有点的发射和吸收情况计算在内，结合光学深度，则其颜色积分公式可变为

(1)

由于在实际的计算机处理中，只能使用离散值来计算式(1)的积分，本文采用Riemann sum近似计算积分，因此有

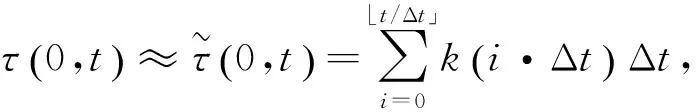
(2)

由式(1)、(2)则有

(3)

定义不透明度A为

(4)

由式(3)、(4)，则有

因此得出光线投射法的离散求值为

(5)

把式(5)写成迭代形式：

(6)

(7)

上述便是发射-吸收模型的光线投射法的颜色合成公式，其中：C′i为累积到第i个体素时的颜色值;A′i为累积到第i个体素时的不透明度;Ci为第i个体素的发射颜色;Ai为第i个体素的不透明度.本文使用式(6)和式(7)进行颜色合成计算.

1.2 基于GPU渲染的空体素跳过

文献[4]提出的光线投射算法，是将体数据保存在3D纹理中，通过渲染方法，分别得到对于3D纹理的前向和后向纹理(亦即光线投射的起点和终点)，通过前后向视图的差值得到光线方向，如图2所示，然后在GPU中进行光线投射的颜色累加操作.

文献[5-6]使用结合数据剖分的方法，在GPU渲染操作之前，通过层次化的数据结构，如八叉树等将体数据进行剖分，根据剖分后的结果进行空体素块的剔除，只保留活跃体素块.然后再利用GPU的渲染功能对所有的活跃体素块分别进行前向和后向渲染，生成前向和后向纹理，分别表示距视点最近和最远点的集合.这种方法可以快速有效的剔除体数据包围盒外表面与有效体素之间的空体素，如图3所示的体数据，渲染后光线r1-r6的有效起点是s1-s6，有效终点为e1-e6，而光线r0则未经过任何有效体素，图3中的灰色区域就可以快速跳过了.但这种方法对于具有较多中空结构的体数据依然无效，如图3中的白色封闭区域，即光线r2-r5所经过的区域，以光线r3为例，其有效起点s3至终点e3之间，有大片的空白体素，由于GPU渲染方法的限制，还是无法进行跳过.

图2 包围盒渲染结果

图3 中空数据集的光线投射过程

2 八叉树

八叉树可以用于层次性体绘制，也可以作为一种数据分块方法，解决可视化时由于数据规模过大而无法全部装载进显存的问题[14].本文使用八叉树除了完成对体数据的剖分，还要在此基础上，按照每个子块的活跃/不活跃性质，剔除不活跃子块，即空体素块，重新构建出一个新的包含有效体素块的顶点数组，以用于进行GPU渲染，最终得到前向和后向纹理.

本文所建立的八叉树的结构定义如图4所示.图4中minValue、maxValue是在八叉树的构建过程中，体数据包围盒被剖分为若干个子数据块，比较每个子块内所有体素的标量值，从而得到该子块中的所有体素标量值的最小-最大值对，做为每个子块的特征之一.除此之外，子块的位置信息positionX，positionY，positionZ，结点深度nodeDepth也是特征之一，它们被用来在建立新的有效体素块顶点数组时计算每个顶点坐标.

八叉树创建完成之后，所有相邻的同质子块会被合并为一个大的子块，从而节省更多的内存资源.

图4 八叉树的结构定义

3 基于体数据剖分的GPU渲染

3.1 GPU渲染

在使用GPU进行渲染之前，需要建立新的体数据顶点集合，遍历八叉树，对每个子块(叶子节点)进行检查，如果为不需要的体素值，即不活跃子块，则将子块从八叉树中剔除；对于活跃子块，则将该子块的8个顶点的坐标加入到新的顶点数组中，最后形成一个新的活跃子块(包含有效体素)顶点数组.

本文使用OPENGL对新的顶点数组进行渲染，为节省内存，提高OPENGL渲染效率，使用了顶点缓冲区来存储生成的顶点数组数据.OPENGL渲染时的空间关系如图5所示.

图5 OPENGL渲染空间关系

为确保渲染后生成的纹理图像每一点的颜色值即为体数据坐标值，从而减少渲染后进行坐标变换而产生的浮点运算，需要将顶点集的坐标归一化到(0，0，0)至(1，1，1)范围内，初始视点坐标为(0.5，0.5，2.5).图6是进行八叉树重构后的渲染结果，可以看出，进行八叉树剖分重构后的结果已经非常接近物体的实际形状了，因此相对于直接对包围盒进行渲染，重构后的体数据可以更快速的进行空体素跳过.

图6 teapot八叉树重构后的渲染结果

3.2 体数据对半剖分

GPU通常使用深度缓冲区的Z值来进行深度检测，对所渲染的体数据中每个体素所对应的Z值进行比较，以决定保留还是剔除.对于未被遮挡的空体素点，由于已经不存在于顶点集合中，GPU不再渲染它们，而对同一视线方向上的2个有效体素点，在近点渲染中，Z值大的点被抛弃；而在远点渲染中，Z值小的被抛弃.一种常用的缓冲区Z值计算公式为

(8)

式中：z为视点到顶点的空间距离；f、n分别为视点到远裁剪面和近裁剪面的空间距离.

如前所述，传统的GPU渲染的方法对于具有中空结构的体数据无能为力，正是因为GPU的深度检测虽然可以检测出部分空体素，但是仅限于那些未被遮挡的空体素，而那些位于中空部分的点则无法被检测到.详细分析此问题，如图7所示，设在当前视点的一条光线上有5个点，其中Sn和Sf分别表示距视点最近和最远的非空体素点，而Se1、Se2、Se3则表示3个空体素点，其中Se2和Se3位于Sn和Sf外侧.当采用近点渲染时，由式(8)计算出每个点的Z值，很显然Se2的Z值比Sn更小，但由于其为空体素，因此依然被剔除；反之同理，当采用远点渲染时，虽然Se3的Z值比Sf更大，但也会被剔除.而Se1在两次渲染过程中由于遮挡均未能剔除.因此可以想到，如果把Se1点也拿到Sn和Sf之外，则遮挡问题也就迎刃而解了.本文提出一种方法，即在GPU渲染前对体数据先进行对半剖分，如图8所示，设断开部分为剖分部位，则对其剖分后的每一部分来说，又产生了新的Sn和Sf，这里记为Sn′和Sf′，可以看到，Se1位于右半部分，且位于原来的远点Sf和新的近点Sn′之外，此时，再进行渲染操作时，Se1也可以被跳过了.再比较对半剖分前后的渲染结果，可以发现，对半剖分前，光线的起点和终点分别是Sn和Sf′，剖分后，其在左半部分的起点和终点变为Sn和Sf，在右半部分变为Sn′和Sf，而Sf′和Sn′之间的空体素则被跳过了，因此，在光线投射过程中，光线实际经过的距离大大缩短.

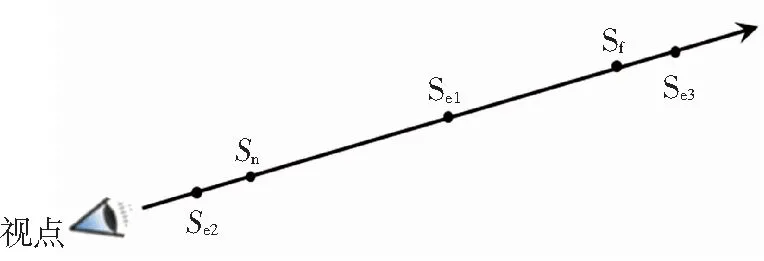
图7 体数据剖分前的状态

图8 对半剖分后的状态

对于图3中的体数据，进行对半剖分后，由一个封闭的中空结构，变成了各自开放的两部分，这里称为V1和V2,如图9所示.由图9可以看出，剖分后的光线r2-r4均跳过了大量中空体素，整个体数据的可视化速度自然就加快了.

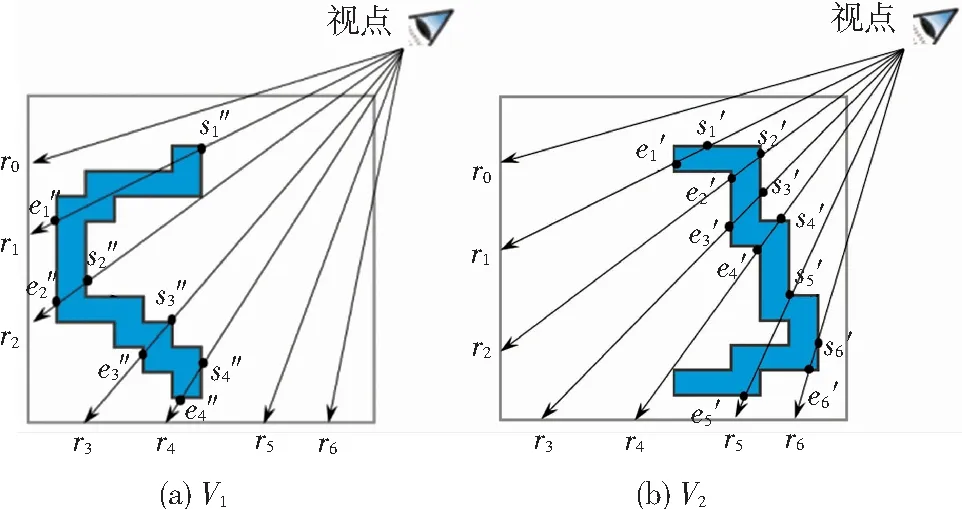
图9 原始体数据剖分后的两部分

对于剖分后的V1和V2两部分，由于每部分只具有原来体数据的1/2有效体素，亦即其各自的另一半被人为掏空了，在后续的光线投射与颜色累积过程中，为保证生成正确的图像，必须保留每部分的位置关系，即保证每部分中所有有效体素的坐标保持不变.为此，本文对被剖掉的部分用空体素来进行填充，因此这种方法会需要增加内存使用量，是一种以空间换时间的方法.

剖分后的V1和V2两部分还需要分别进行建立八叉树和剔除空块、建立新的有效顶点数组的操作，才可以进行前向和后向渲染.

4 CUDA绘制

CUDA核函数是由多个线程组成的多个线程块的网格，同一个线程块中的线程可以方便的进行通信.针对本文实验所使用的数据分辨率、生成图像大小，以及CUDA设备的实际计算能力，在启动CUDA核函数前，CUDA线程块的大小设置为(16,16)，网格大小为(16,16).

需要注意的是，由于渲染后的前向和后向纹理是由OPENGL生成的，而OPENGL中的纹理在CUDA中无法直接使用.本文通过OPENGL和CUDA的互操作方法，使用CUDA的内存注册和映射机制将OPENGL纹理映射为CUDA中的数组，然后在CUDA中再绑定为CUDA纹理，这种方法可以节省很多数据在内存中的复制时间，提高内存使用率和算法效率.同样的，为接收CUDA核函数返回的最终结果，并使用OPENGL进行绘制显示，同样要将OPENGL中的PBO(pixelbufferobject)映射到CUDA中的数组中，这样CUDA核函数计算的结果也就可以被OPENGL实时接收并显示了.

具体算法过程如下：

1)读入完整体数据，将其从中间部位剖分成两部分V1和V2.

2)分别对V1和V2建立八叉树，并进行空体素块剔除，建立两个新的有效体素块顶点集合.

3)使用GPU分别对新建立的V1和V2的顶点集合进行前向和后向渲染，并保存到纹理中，最后得到V1的前向和后向纹理，V2的前向和后向纹理共4个纹理.

4)通过OPENGL和CUDA互操作，将步骤3)得到的纹理映射到CUDA中，以供CUDA使用.

5)启动CUDA核函数，依次对V1和V2进行光线投射，两部分光线投射的起点和终点可以从步骤3)中得到的纹理结果中读取.

6)在核函数中将得到的两个结果进行合成，并映射到OPENGL纹理，得到最终图像.

其中，步骤5)中的CUDA核函数的具体算法流程如图10所示，算法包括两个相对独立的子过程，分别获取V1和V2的光线起止点和光线方向，完成各自的颜色和透明度累积过程，最后将两个过程的结果累加，得到最终图像.

5 结果与分析

实验所用的计算机配置如下：2.6GHz双核CPU，4G内存，编程环境为VisualStudio2008，显卡采用GeForceGT635M，1G显存，拥有2个SM(streammultiprocessor)，96个CUDA核心，CUDA计算能力2.1，CUDA版本5.5.

共使用了两组数据进行实验，分别为脚趾骨(foot)和茶壶(teapot)，CT数据尺寸均为256×256×256，为对本文方法进行验证和评价，本文实现了文献[4]的基于GPU渲染的方法以及文献[10]中的八叉树编码方法，并将结果与本文提出的方法进行了比较.teapot数据集的图像对比结果如图11(a)～(c)所示，foot数据集如图11(d)～(f)所示.由上至下分别为Westermann方法(简称W方法)、八叉树方法以及本文方法.

图10 CUDA核函数流程

图11 3种方法生成图像对比

3种方法的数据预处理时间见表1.文献[4]方法由于无须创建八叉树结构，只需要消耗体数据的装载时间，因此所需要的预处理时间最短.本文方法的预处理时间少于八叉树编码方法，这是由于本文剔除空块操作与构造八叉树是同时进行的，因此可以节省更多的预处理时间.在实际可视化应用中，图像在绘制阶段的成像时间更为重要，因此，相对于获得更为满意的加速效果，预处理时间的有限增加是可以接受的.

表1 数据预处理时间比较 ms

3种方法的核函数运行时间对比见表2, 3.表中的加速比分别为八叉树编码方法和本文方法相对于文献[4]方法的加速百分比.

从成像效果看，3种方法没有明显差异.对于teapot数据集，由于茶壶是中空结构，其内部具有较多的空体素，由核函数运行时间可以看出，因此本文提出的对半剖分方法相较于另外两种方法，均有非常显著的加速效果，且光线投射步长越小，加速效果越明显；而对于foot数据集，加速效果则相对不太明显，这是因为脚趾骨的结构不是中空的，内部很少有空体素可以跳过.

表2 foot数据集核函数运行时间对比

表3 teapot数据集核函数运行时间对比

6 结 论

1)通过改进的八叉树层次分解方法，将体数据进行重构，使数据表达和存储更加高效和易于处理.

2)提出一种将原始体数据先对半剖分成两部分再分别进行渲染以跳过中空部分体素的方法，使得在光线投射过程中，最大程度的减少因空体素计算导致的冗余计算问题.

3)结合使用GPU硬件渲染的方法，快速跳过在体数据包围盒外部的空体素，节省了传统光线投射算法中手动计算光线与包围盒交点而浪费的时间.

4)实验结果表明，本文提出的方法生成的图像质量和传统的方法没有明显差别，但可以有效的跳过中空体素，对于中空结构的体数据的可视化具有明显的加速效果.

[1] LEVOY M. Display of surface from volume data [J]. IEEE Computer Graphics & Application, 1988, 8(3):29-37.

[2] CULLIP T J, NEUMANN U. Accelerating volume reconstruction with 3D texture hardware. Technical report, TR93-027 [R]. NC, USA: University of North Carolina at Chapel Hill, 1994.

[3] CABRAL B, CAM N, FORAN J. Accelerated volume rendering and tomographic reconstruction using texture mapping hardware[C]//Proceedings of the 1994 Symposium on Volume Visualization. York, NY: ACM, 1994:91-98.

[4] KRUGER J,WESTERMANN R. Acceleration techniques for GPU-based volume rendering [C]// Proceedings of the 14thIEEE Visualization 2003 (VIS′03). Washington, DC: IEEE Computer Society, 2003: 38.

[5] SCHARSACH H, HADWIGER M, NEUBAUEr A, et al. Perspective isosurface and direct volume rendering for virtual endoscopy applications [C]//Proceedings of Eurographics/ IEEE-VGTC Symposium on Visualization. Lisbon, Portugal: The Eurographic Association, 2006: 315-322.[6] HADWIGER M, LJUNG P, SALAMA C R, et al. Advanced illumination techniques for GPU volume raycasting [C]//Proceedings of the ACM Special Interest Group on Computer Graphics and Interactive Techniques. New York: ACM, 2008.

[7] QIAN Fengchen, SHAN Ning, YE Yalin. A model of point multiresolution rendering method [C]// International Conference on Structural Engineering, Vibration and Aerospace Engineering (SEVAE 2013). Zhuhai: Trans Tech Publications LTD, 2014, 482: 355-358.

[8] 刘白林, 黄舒舒, 刘云卿. 八叉树编码与GPU加速结合的光线投射法 [J]. 西安工业大学学报, 2011, 31(1):65-68.[9] LIU B Q, CLAPWORTHY G J, DONG F, et al. Octree rasterization: accelerating high-quality out-of-core GPU volume rendering [J]. IEEE Transaction on Visualization and Computer Graphics, 2013, 19(10):1732-1745.

[10]康健超, 康宝生, 冯筠, 等. 基于八叉树编码的CUDA光线投射算法[J]. 西北大学学报:自然科学版, 2012, 42(1):36-41

[11]BERGNER S, MOLLER T, WEISKOPF D, et al. A spectral analysis of function composition and its implications for sampling in direct volume visualization [C]//IEEE Transactions on Visualization and Computer Graphics. Piscataway, NJ：IEEE Educational Activities，2006, 12(5):1353-1360.

[12]SUWELACK S, HEITZ E, UNTERHINNINGHOFEN R, et al. Adaptive GPU ray casting based on spectral analysis[C]// Proceedings of the 5thInternational Conference on Medical Imaging and Augmented Reality. Berlin, Heidelberg: Springer-Verlag, 2010: 169-178.

[13]叶良, 单桂华, 迟学斌. 基于CUDA加速的光线投射法研究 [J]. 图像图形技术研究与应用, 2010: 235-240.

[14]苏超轼, 赵明昌, 张向文. GPU加速的八叉树体绘制算法 [J]. 计算机应用, 2008, 28(5):1232-1235.

(编辑 张 红)

GPU-based ray casting method by half-splitting volume data

YU Shui，WANG Kuanquan，XIA Yong，ZHANG Henggui

(School of Computer Science and Technology, Harbin Institute of Technology, 150001 Harbin, China)

To alleviate the inefficiency of the current visualization methods in skipping the empty voxels located in the hollow part, this paper presents a GPU-based ray casting method for hollow volume data. First, the volume is divided into two equal parts and reconstructed into two octrees before rendering. In this process, the empty blocks are culled synchronously from the original data, and two vertex arrays are generated consisting of valid voxels only. Then, the vertex arrays are rendered into textures which contain the start and direction information of the ray. The final images are obtained by calculating the color and opacity of the two parts with CUDA, respectively. The experimental results show that our method can speed up the rendering speed considerably on the volume data with large hollow structure without any quality loss compared with the traditional visualization methods.

data visualization; ray casting; GPU rendering; octree; CUDA; hollow volume data

10.11918/j.issn.0367-6234.2016.04.012

2014-09-23.

国家自然科学基金(61173086)；山东省科技发展计划资助(2012GSF12105).

于 水(1976—)，男，博士研究生；

王宽全(1964—)，男，教授，博士生导师；

王宽全，wangkq@hit.edu.cn.

TP391.41

A

0367-6234(2016)04-0073-06

张恒贵(1964—)，男，教授，博士生导师.