顶管结构荷载分布模式研究

李 宏，黄俊，陈立平，张忠宇，吴子瀛

（苏交科集团股份有限公司，江苏 南京 210017）

顶管结构荷载分布模式研究

李 宏，黄俊，陈立平，张忠宇，吴子瀛

（苏交科集团股份有限公司，江苏 南京 210017）

顶管法作为一种非开挖的施工技术得到了越来越广泛的运用，但是针对顶管结构荷载分布模式的认识目前还比较模糊，文章对比分析了分析了日本、美国、德国和中国规范中顶管荷载的计算，并结合工程实际情况，对顶管荷载分布模式进一步研究，结果表明：顶管结构受力具有典型的时空效应；在稳定的地层中，顶管荷载主要来源于结构自重；在不稳定地层中，顶管上部荷载来源于结构自重和地层压力；施工期间顶管在长度方向上荷载分布存在较大差异，对于一般的地层，沿长度方向上的荷载呈前小后大的分布趋势。

顶管工法；荷载分布模式；管土作用

1 概述

随着国民经济的飞速发展以及城市化进程的不断推进，地下空间的利用和开发越来越受到重视。顶管法可以在不开挖地面的情况下进行管道铺设，优势非常明显，因此在管道施工中应用相当广泛。顶管施工过程中，管片结构受力一直以来都倍受关注，因其直接关系到顶推力的计算，管节设计，从而进一步影响到顶管工作始发井、中继间和后靠背的设计［1］。

顶管结构受力涉及到复杂的管土相互作用，比较有代表性的假设是Haslem提出的挖掘面稳定假设［2-3］和O'Reilly与Rogers提出的管土全接触假设［4］。前者认为顶力主要由管道自重产生的摩擦阻力组成；后者认为顶力主要用来克服由作用在管周的土压力引起的摩擦阻力，这2种假设实际提出了2种不同的管土接触状态。国内外学者通过对实际工程中的管土相互作用力进行研究，并对比了这2种理论的预测效果。Kastne和Pellet［2］通过对几座实际工程实测结果的分析，发现管土全接触假设在大部分下与实测结果较为一致。Sofianos［5］等通过对希腊雅典排水顶管工程的监测，对两种假设进行对比分析，结果表明，在挖掘面比较稳定的情况下，可以认为管土只在底部接触，随着推进距离的增加。

国内近几年在顶管荷载研究方面也取得了不少成果，魏纲等通过实测结果，提出管土接触压力随管道的顶进一开始缓慢上升，到一定距离后基本保持在一定范围内［6］。张坤勇等给出了一种适用于描述任意位移荷载条件下管线的解析解公式［7］。高惠瑛、冯启民等分析了管-土摩擦角等多个参数对管道的影响［8］。冯启民、赵林考虑管土相互作用，分析了管道作为薄壳结构的有限元模型与断层位错反应［9］。朱庆杰等通过ADINA软件的应用，探讨了三维有限元管土融合建模方法，初步分析了管土摩擦系数和管径对地下管道破坏的影响［10］。杨敏考虑管道两侧填土分担上部荷载作用，认为土体达到主动极限破坏，提出了沟填式柔性管道土压力计算公式［11］。李永刚假定回填无黏性土，通过试验测定沟埋式刚性矩形截面涵洞顶的竖向土压力值再进行相应的理论分析研究提出新的土压力计算模型及方法［12-13］。申文明等针对无黏性填土，按1∶1的比例建造了上埋式管涵模型，进行了土压力的现场测试。通过对比不同埋深试验工况测试结果，发现管顶管土土界面竖向土压力在管顶中心线最大两侧最小的现象进而引入拱效应系数［14］。

2 国内外顶管规范中的荷载模式

各国顶管规范对顶管结构荷载模式的规定不尽相同，比较有代表性的是日本、美国、德国和中国的相关规定。

2.1 日本规范［15］

日本相关规范对钢筋混凝土顶管的受力模式规定如图1所示。地基反力与竖向土压为均布荷载，当埋置深度小于1～2倍管径时，无需考虑土拱效应。

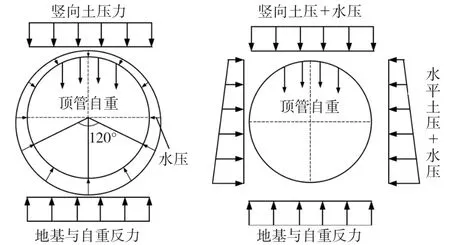
图1 顶管结构受力模式

当地基土为黏性土（N＞8），埋置深度大于1～2倍管径时，利用公式（1）将地基当做均质或者多层地基进行计算；对于软弱黏土（N＜2）地基，忽略黏聚力作用。施工时仅考虑水压力作用，投入运营后的侧向水土压力为梯形分布，随深度的增加而增加。

式中：K为土体侧压力系数；c为黏聚力；s为地层重度；μ为管土摩擦系数；H为管顶埋置深度；B为滑动土体的宽度；D为顶管外径。

地基反力为均布力，其大小为管道自重与上覆土压力之和再减去水浮力，地基反力在施工时的支承角为120°，投入运营后为180°。

2.2 美国规范［16］

美国相关规范中垂直土压力采公式（3）进行计算，根据不同土质选取不同的经验系数，具体取值方案如表1所示。水平向土压力为均布荷载，其计算方法是按照竖向荷载乘以侧压经验系数，系数取值与施工过程和方法有关，如表2所示。地基反力为均布，施工方法不同，选取的支承角也不同。其受力分布模式见图2。

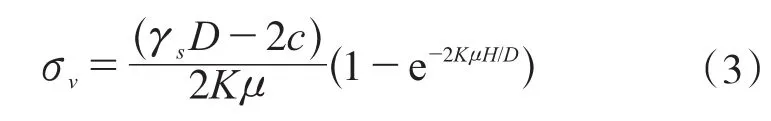
式中：μ为管土摩擦系数；c为地层黏聚力；K为土侧压系数；s为地层平均重度；H为管顶埋置深度；D为顶管外径。

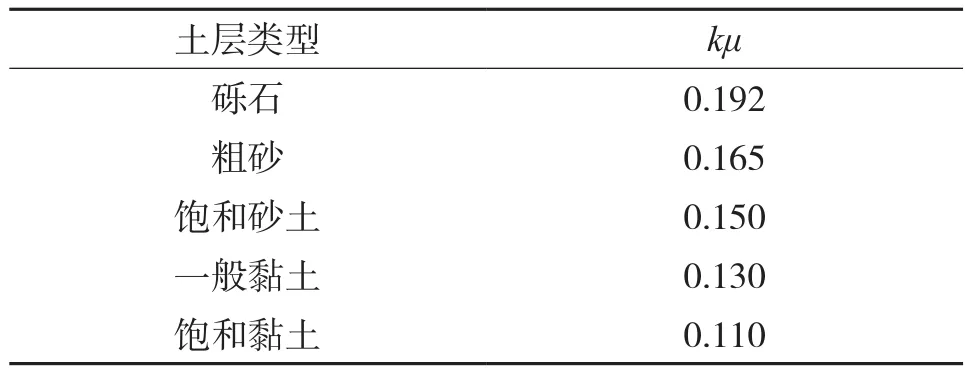
表1 不同土层kμ系数

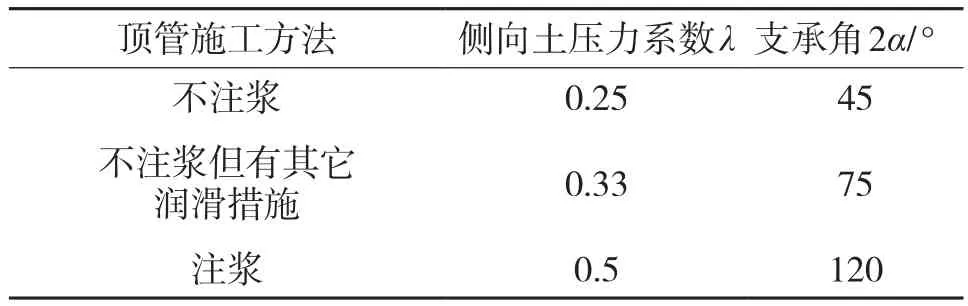
表2 侧向土压力系数和支承角

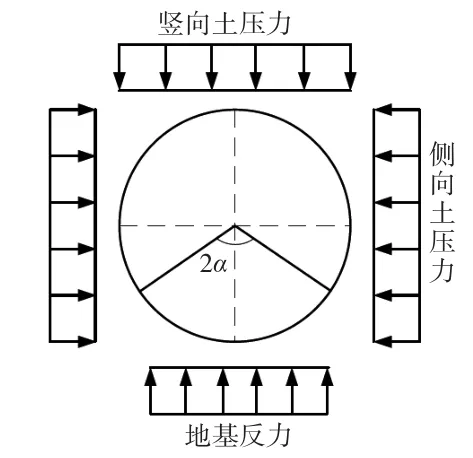
图2 顶管结构受力模式（美国规范）

2.3 德国规范［17］

德国顶管规范中，采用余弦分布荷载模式对顶管荷载进行分析（见图3），竖向荷载引起的地基反力采用克莱茵分布，支承角统一为180°。当不考虑地下水时，管道顶端土荷载为太沙基松动土压力（公式1），在忽略黏聚力影响的情况下，滑动带条宽度为3倍管径；当考虑地下水时，利用土柱理论对荷载进行计算。侧向土压力采用经验系数法计算：

经验系数一般情况下取0.3～0.5；无注浆环境取0.3；注浆环境取0.4。对于没有采用注浆作业的顶管施工结束后，系数取0.4；注浆作业的管道后期系数取0.5。

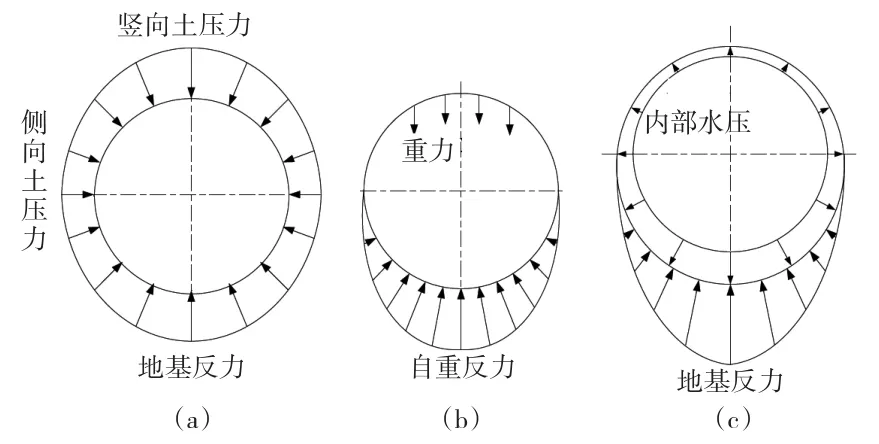
图3 顶管结构受力模式（德国规范）

2.4 中国规范［18-19］

我国《给水排水工程顶管技术规程》规定：当管顶埋置深度小于等于1倍管径（或地层均为淤泥质），竖向土压利用土柱理论进行计算；除上述情况外都按式（5）～式（7）计算：

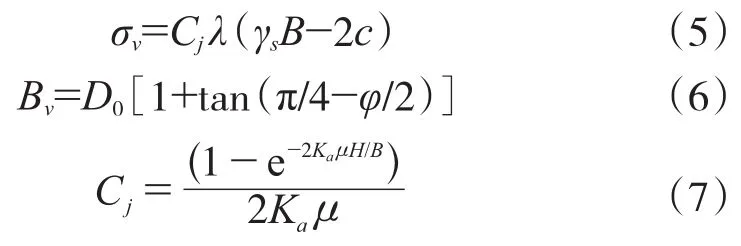
式中：B为滑动带条宽度；Cj为顶管竖向土压系数； Ka为原状土的主动土压力系数与内摩擦系数的乘积。

通常情况下黏性土为0.13，砂和砾石可为0.165，饱和黏土为0.11。当无地下水影响时，侧向土压力可按式（8）计算：

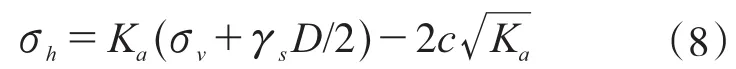
当管道处于地下水位以下时，则需考虑地下水的影响，此时采用水土分算，土压力按式（8）计算，重度取有效重度；水压力按静水压力进行计算。规程中没有给出明确的管道的受力模式图示，参照开槽埋管的设计方法，管道基座支承角取为120°，其受力模式如图4所示，地基反力为克莱茵分布，侧向土压力为均匀分布。

图4 顶管结构受力模式（中国规范）

2.5 比较分析

分别从竖向土压、侧向土压、地基反力三方面对各国规范进行差异性比较，具体如下：

（1）垂直土压力

美国规范利用马斯顿公式计算，中国规范采用滑移带理论，公式经过一定改进；日本和德国都是采用太沙基松动土压力理论。

（2）侧向土压力

日本规范将顶管施工前后的荷载分开考虑，取最不利者进行管道计算；日本、美国、德国规范比较相似，对侧向土压力都采用经验系数进行计算；中国规范是根据土的主动侧压系数进行计算。

（3）地基反力

地基反力分布模式分为两大类，日本和美国规范中为均布；德国和中国规范为克莱茵分布，不同之处在于支承角的不同。

3 实际顶管结构荷载模式

以上各国规范对顶管荷载模式的规定与实际情况其实是存在一定差别的，实际荷载与土层的性质有很大关系。当顶管地层的稳定性较好时，由于顶管机头和顶管之间存在径差，顶管与周围土层之间存在一定间隙（见图5），在采用泥水平衡法进行顶管施工时，泥水充填在这个间隙中，泥浆不仅起到润滑作用，而且还起到稳定土体的作用［20］。

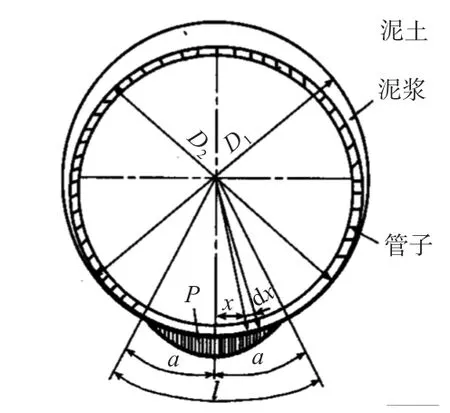
图5 顶管与地层的接触状态

通常情况下当地层的稳定系数Ns≤6时，土层能够自稳，管节上部间隙能够维持；当间隙填充泥浆后，土层的稳定性可以增加，间隙能够维持较长时间，地层的稳定系数可以利用式（9）进行简化计算：

式中：σT为顶管土层隧道内的平衡压力；Cu为顶管地层土的无排水剪切强度。

在稳定性较好的地层中，当泥浆的压力足够大时，顶管结构悬浮于泥浆中之中，这是一种最为理想的状态，此时顶管受力较为均匀。但在实际顶管施工中，顶管结构在重力作用下会发生沉降，下部与土层接触，上部间隙则被顶管泥浆充填。稳定地层的顶管荷载简化如图6所示。

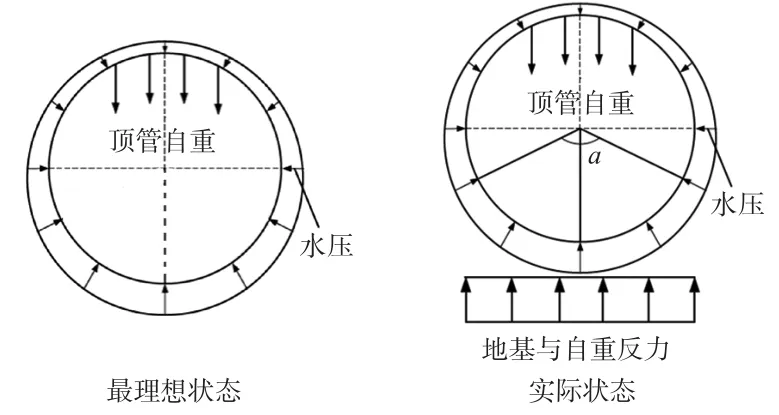
图6 不同情况下的顶管结构受力状态

由于地层变形具有一定的时空效应，通常情况下，随着顶管的进一步推进，后方顶管的上部空隙会逐渐闭合，从而与土体接触并产生接触压力，因此实际顶管在长度上的荷载分布模式为前段小，后段大，如图7所示。

沿长度方向荷载分布规律与土体稳定性密切相关，土体稳定时间的长短决定了顶管上部与地层接触段的长度，从而影响到荷载分布曲线的形状。结合前述各国现行规范中有关顶管荷载的规定，可以发现，当前还没有一个国家规范考虑到了顶管施工工程的时空效应。

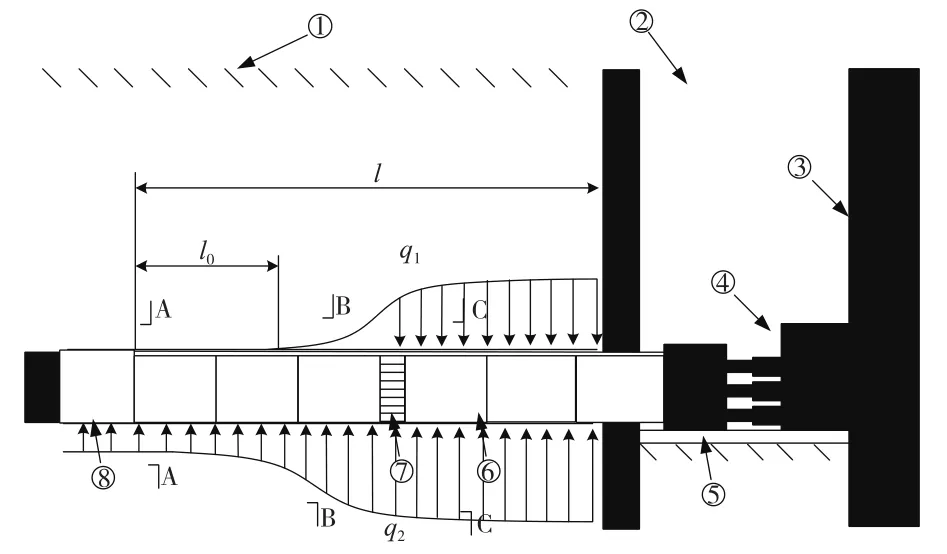
图7 顶管沿长度方向的受力状态

4 顶管结构荷载计算方法

顶管径向荷载取决于其自身重量和管土相互作用力，根据围岩变形时空效应，可以利用以下分析步骤（见图8）对其荷载分布进行计算。具体过程如下：

（1）初始参数获取

首先根据实际工程获取如下初始参数：地层压缩模量Es、泊松比μ、内摩擦角φ、顶管埋深h、顶管机外径D0、管节外径D1、单位长度管节自重ω。

（2）释放荷载计算

释放荷载表示围岩在开挖后由于失去约束而出现变形发展，逐渐松弛而导致的松弛减小的荷载，在开挖前其释放荷载为0，在时间无限长后释放荷载等于上覆围岩自重（浅埋情况）或塌落拱内岩土体自重（深埋）。由于顶管通常埋深较浅，因此选用浅埋情况，松弛荷载与时间的关系假设如下：

图8 顶管荷载计算流程

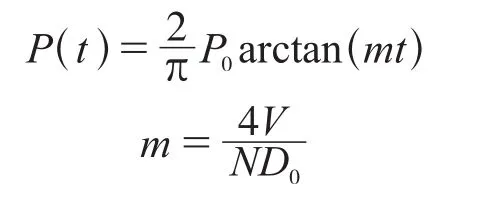
式中：P（t）为松弛荷载；V为平均推进速度；D0为顶管机外径；P0为上覆围岩自重。

（3）围岩变形计算

（4）接触荷载计算

在得到分界长度l0和对应的时刻t0后，就可以对管土作用荷载进行计算。在管土接触分界长度l0=Vt0之前，管土没有接触时，只考虑顶管下部自重荷载，此时Pr=ω；在在管土接触分界长度l0=Vt0之后，管土已经接触，此时

上部与下部之间可简化为线性过度，接触前后顶管荷载分布模式如图9所示。

利用以上4个计算分析步骤就可以对顶管任意位置截面的荷载分布进行计算。图9所得荷载与日本规范较为相似，但不同之处在于，本文方法考虑了围岩变形的时空效应，可对不同释放荷载下的截面径向应力进行定量计算，能够计算顶管结构在不同位置的荷载；而日本规范将顶管荷载在任意位置视为相同，没有考虑围岩的变形特性。

图9 顶管不同截面荷载分布特性

由于岩土材料力学特性极为复杂，本文还有许多不完善的地方，如松弛荷载计算以及荷载环向分布规律等都需要进一步研究。

5 结论

（1）顶管结构受力涉及到复杂的管土相互作用，且与地层稳定性密切相关，具有典型的时空效应。

（2）在稳定的地层中，顶管上部不与地层直接接触，荷载主要来源于结构自重；在不稳定地层中，顶管上部与变形或垮塌的土体直接接触，上部荷载来自于结构自重和地层压力。

（3）施工期间顶管在长度方向上荷载分布存在较大差异，对于一般的地层，沿长度方向上的荷载呈前小后大的分布趋势。利用本文分析的4个步骤可对任意位置顶管荷载进行计算。

［1］陈楠.复杂环境中大直径钢顶管的受力特性研究［D］.上海，上海交通大学，2012.

［2］Pellet B A L，Kastner，R. Experimental and analytical study of friction forces during microtunnelling operations［J］. Tunnelling and Underground space Technology，2002，（17）：83-97.

［3］Haslem R F. Pipe-jacking forces：from practice to theory［C］∥Infrastructure renovation and waste control. ICE North Western Association Centenary Conference，Manchester，Manstock，1986.

［4］O'Reilly M P，Rogers C D F. Pipe jacking forces［C］∥In Proceed. International. Conference. On Foundations and Tunnels 87，Edinburgh，1987.

［5］ Sofianos A I，Loukas，P，Chantzakos，C Pipe jacking a sewer under Athens［J］. Journal of Tunnelling and Underground Space Technology，2004（19）：193-203.

［6］魏纲，徐日庆，余剑英，等.顶管施工中管道受力性能的现场试验研究［J］.岩土力学，2005，26（8）：1273-1277

［7］张坤勇，王宇，艾英钵，等. 任意荷载下管土相互作用解答［J］.岩土工程学报，2010，32（8）：1189-1193.

［8］高惠瑛，冯启民.场地沉陷埋地管道反应分析方法［J］.地震工程与工程振动，1997，17（1）：68 -75.

［9］冯启民，赵林.跨越断层埋地管道屈曲分析［J］.地震工程与工程振动，2001，21（4）：80 -87.

［10］朱庆杰，刘英利，蒋录珍，等.管土摩擦和管径对埋地管道破坏的影响分析［J］.地震工程与工程振动，2006，26（3）：197-199.

［11］杨敏，陈剑锋，刘全林.开槽埋设柔性管竖向土压力计算探讨［J］.特种结构，2007，24（3）：27-29.

［12］李永刚，李珠，张善元.矩形沟埋涵洞顶部垂直土压力［J］.工程力学，2008，25（1）：155-160.

［13］李永刚，张善元.矩形沟埋涵洞顶部垂直土压力试验和理论研究［J］.岩土力学，2008，29（4）：1081-1086.

［14］申文明，边学成，唐晓武等.低填方上埋式管涵土压力的模型试验和理论研究［J］.岩土工程学报2010，32（7）：1017-1022.

［15］超大口径PC推进工法,超大口径PC推进工法研究会.［M］. 2010.

［16］ ASCE 27-00，Standard practice for direct design of precast concrete pipe forjacking in trenchless construction［S］. ASCE，1980.

［17］ATVA-161，Structural calculation of driven pipes［S］. Berlin：Springer，2005.

［18］李辉，王成.注浆减摩技术在顶管施工中的应用［J］.水运工程，2010，439（3）：144-146.

［19］GB 50332—2002给水排水工程管道结构设计规范［S］.

［20］杨文义.砂质黏土层中泥水平衡顶管施工顶力分析［J］.煤炭学报，2006，31（2）：159-162.

Research on Load Distribution Pattern of Pipe Jacking Structure

Li Hong, Huang Jun, Chen Liping, Zhang Zhongyu, Wu Ziying
（JSTI Group, Nanjing 210017, China）

Pipe jacking has been widely used as a trenchless construction technology, but understanding for structure load distribution is still relatively vague. In this paper, load calculation of pipe-jacking in specifications of Japan, the United States, Germany and China are compared, combining with engineering practice the load distribution patterns are further reasearched. The results show that the structure mechanics model has typical time-space effect; in stable stratum, the pipe-jacking load is mainly from gravity load, in unstable stratum, the load is from gravity load and formation pressure; there are large differences in load distribution in the longitudinal direction, for general stratum, the load is becoming smaller when it comes closer to the front of pipe-jacking.

pipe jacking method; load distribution pattern; interaction between soil and pipe

U449.1

A

1672-9889（2016）05-0059-05

2015-12-23）

李宏（1978-），男，浙江舟山人，高级工程师，主要从事隧道与地下工程设计与科研相关工作。