基于复Givens矩阵与蝙蝠优化的卷积盲分离算法

贾志成，韩大伟，陈雷，郭艳菊，许浩达

(1. 河北工业大学电子信息工程学院，天津 300401；2. 天津大学精密仪器与光电子工程学院，天津 300072；3. 天津商业大学信息工程学院，天津 300134)

基于复Givens矩阵与蝙蝠优化的卷积盲分离算法

贾志成1，韩大伟1，陈雷2,3，郭艳菊1，许浩达1

(1. 河北工业大学电子信息工程学院，天津 300401；2. 天津大学精密仪器与光电子工程学院，天津 300072；3. 天津商业大学信息工程学院，天津 300134)

针对传统卷积混合盲分离待求参数多、分离效果易受分离矩阵初值影响的局限性，提出了基于复Givens矩阵与蝙蝠优化的频域求解算法。算法采用复Givens矩阵表示分离矩阵，减少了待求参数，降低了求解难度和计算量。利用蝙蝠算法代替梯度算法优化求解旋转角度完成各频点线性瞬时混合复信号的盲分离，全局收敛性更强。此外，由于对源信号的先验知识要求较少，可以分离服从多种分布的信号。仿真实验表明，该算法可有效地实现卷积混合盲分离。

盲分离；卷积混合；蝙蝠算法；复Givens矩阵

1 引言

盲分离是指在缺乏源信号和传输信道参数先验知识的情况下，仅依据观测到的混合信号分离出源信号的过程[1]。盲分离主要有线性瞬时混合和卷积混合2种类型，线性瞬时混合因为原理简单而得到广泛的研究，许多有效分离方法被提出[2～4]。然而在现实环境中，传感器所接收到的真实信号一般为各个源信号经过衰减和时延后的卷积混合信号。因此，卷积混合盲分离开始逐渐受到了学者们的更多关注。

目前，解决卷积混合盲分离的方法有时域求解和频域求解 2种形式。时域方法[5,6]由于要用到卷积运算，随着滤波器长度的增加，计算量增长较快。相较而言，频域方法把时域信号转化到频域进行分离，计算量较小，是近几年的研究热点。但是大部分频域算法存在以下局限性：1) 求解中需要进行非线性函数或概率密度函数的选取[7～9]，对源信号的先验知识要求较高；2) 优化算法主要采用梯度类方法[8～10]，需要进行步长的选取且分离矩阵初值不合理时易陷入局部收敛，影响分离性能。

针对已有卷积盲分离算法的上述不足，本文提出基于复Givens矩阵与蝙蝠优化的频域求解方法。算法选用复数域峭度作为目标函数，避免了非线性函数和概率密度函数选取的问题，对源信号的先验知识要求较少，可适用于多种分布信号的分离。进而利用蝙蝠算法代替传统的梯度类优化算法对目标函数进行优化求解，避免了步长及分离矩阵迭代初值的确定，分离算法的全局收敛性能更好。其中，为减少分离矩阵中未知参数的个数，利用QR分解理论，将分离矩阵的求解转化为复Givens矩阵中旋转角度的求解，降低了求解难度和算法计算量。

2 信号卷积混合模型

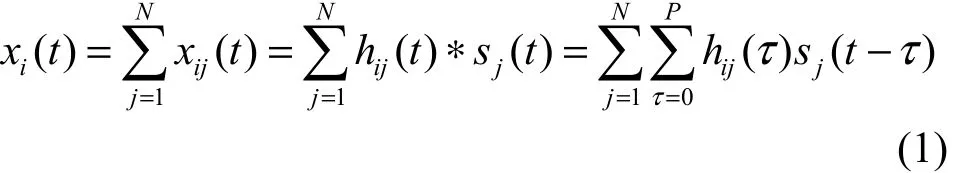
其中，t为离散时间，N为源信号个数，hij为第 j个源信号到第 i个麦克风的冲激响应，*为卷积运算，P为滤波器阶数。为了在频域求解卷积混合盲分离，用STFT（short-time Fourier transform）将式(1)中的时域卷积混合信号转换到频域，可得

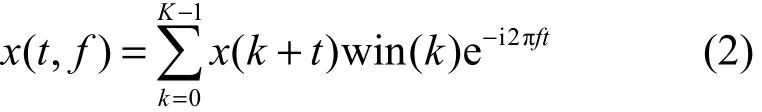
其中，K为STFT的点数，win(k)为窗函数，各频点频率值其中，f为

s采样频率。若窗函数win(k)的长度比滤波器的长度P大得足够多，频域卷积混合信号近似为

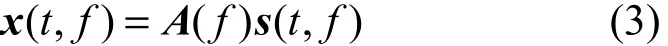
其中， x(t, f) =(x( t, f ),… ,x (t, f ))T为频域中混合

1

M信号， K( s3( t)) = 22.9843 > 0为频域中源信号，M、N分别为混合信号与源信号的个数，A(f)为频域中混合矩阵。由式(3)可知，时域源信号的卷积混合经STFT转换为各频率点的线性瞬时混合，可利用线性瞬时混合盲分离方法求解各频点的分离信号。分离模型如式(4)所示。

其中， y(t, f ) =(y( t, f ),… ,y (t, f ))T为频域中分离

1

N信号，W(f)为频域中分离矩阵。

3 蝙蝠算法

蝙蝠算法[11]是Yang于2010年提出的一种新型群智能算法，该算法利用回声定位的原理搜索食物的最佳位置，是一种非常有效的优化算法。相较粒子群算法、蚁群算法和蜂群算法等仿生智能算法，蝙蝠算法的收敛速度更快，寻优能力更强，已应用于工程设计、组合优化、神经网络等诸多领域[12～14]。蝙蝠算法每次迭代进化的频率、速度和位置更新公式如下

其中，fp为第p只蝙蝠的频率，fmin、 fmax分别为频率的最小值和最大值分别为第p只蝙蝠在第q次和第q−1次迭代的速度和位置，x∗为最优位置， β为[0,1]内满足均匀分布的随机向量。每次迭代找出最优解后，通过判定，依据式(6)在其周围进行局部搜索，产生新解。

其中，ε为[-1,1]的一个随机数，qA为所有蝙蝠在此次迭代中的平均音强。通过比较选择是否接受这个新解，若新解优于当前最佳解，依据式(7)进行脉冲频率和脉冲音强的更新。

4 基于蝙蝠优化的卷积混合盲分离算法

本文算法将时域卷积混合信号经STFT转换到频域进行求解，此时，信号由卷积混合转换为复数域下各个频率点的线性瞬时混合。首先利用QR分解理论，将各频率点的分离矩阵用复Givens矩阵表示，然后用蝙蝠算法优化求解复Givens矩阵中的旋转角度完成各频率点的盲分离。最后，对各频率点的分离信号进行顺序和比例模糊性消除，经ISTFT得到最终时域源信号的估计。算法原理如图1所示。

4.1 用复Givens矩阵表示分离矩阵

时域卷积混合信号经STFT后，转化为各频率点的复数域线性瞬时混合信号。为减少分离求解的变量数目，从而降低求解难度和算法计算量。分离之前，首先对混合矩阵进行QR分解可得

其中，v(t, f)为预处理后的混合信号，P(f)为白化阵，Q(f)为酉阵，R(f)为上三角阵。因预处理实现了信号的去相关，所以

基于源信号之间相互独立这一假设，源信号之间必不相关，所以 E{s( t, f) sH(t, f) }=I，可得R(f)为酉阵。由R(f)既为上三角阵，也为酉阵，可以推导出其为对角阵，所以式(8)可转换为

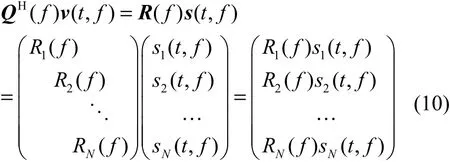
图1 基于复Givens矩阵与蝙蝠优化的卷积盲分离算法

所求的信号与源信号成比例关系，所以可以作为对源信号的估计，即为分离信号。将式(10)与式(4)对照可得，QH(f)即为分离矩阵W(f)的估计。因为QH(f)为酉阵，即正交阵在复数域的扩展，由文献[15]，正交阵可由Givens矩阵连乘的形式表示，扩展到复数域分离矩阵W(f)表示如下

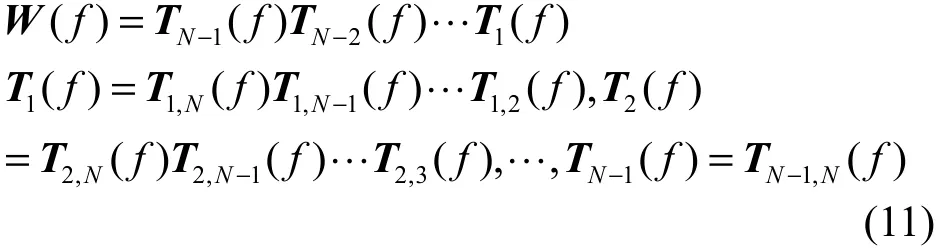
其中， Ta,b(f)为N阶复Givens矩阵，复数形式的Givens矩阵定义为[16]

其中，N为矩阵阶数，即信号路数， c= cosθ,d= sinθ ，θ为旋转角度且满足θ1+ θ4= θ2+ θ3。因为θ1+ θ4= θ2+ θ3这一约束条件，可以减少 1个未知参数，因此每个复Givens矩阵的未知参数个数为4。又因为T1(f)包含N−1个复Givens矩阵，T2(f)包含N−2个复Givens矩阵，依此类推，TN−1(f )包含1个复Givens矩阵，而每个复Givens矩阵含有4个未知参数，所以分离矩阵W(f)用复Givens矩阵连乘表示后，未知参数个数为

而如果不用复Givens矩阵连乘表示复值分离矩阵W(f)，因为W(f)是N阶的，而且每个元素都是复数形式的，含 2个未知参数，所以包含未知参数个数为22N。因此用复 Givens矩阵连乘表示分离矩阵W(f)后可以减少的未知参数个数为

对于3路信号，即N=3时，分离矩阵W(f)可表示如下

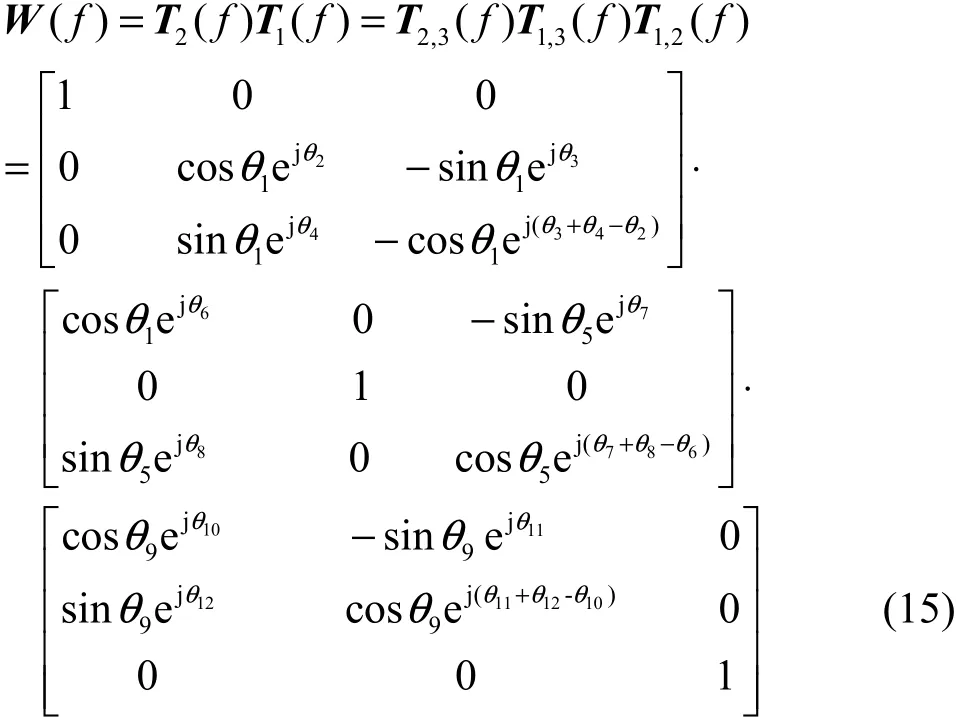
将分离矩阵表示为复Givens矩阵连乘的形式，未知参数个数为12，若不用复Givens矩阵，因分离矩阵为3阶复矩阵，未知参数个数为18，可减少6个未知参数。

由以上分析可知，依据QR分解理论，本文算法把对分离矩阵的求解转化为对复 Givens矩阵中旋转角度的求解。不仅可以保证复数域下分离矩阵的正交性，提高求解精度，而且可以减少未知参数2N个，大大简化了求解难度，降低算法计算量。

4.2 用蝙蝠算法优化复Givens矩阵中旋转角度

将各频率点的分离矩阵用复Givens矩阵表示，对分离矩阵的求解转化为对 Givens矩阵中旋转角度的求解。本文采用蝙蝠算法优化复Givens矩阵中的旋转角度，经多次迭代，当目标函数即蝙蝠算法的适应度函数取得极值时，所得到蝙蝠的最佳位置即为分离矩阵的解。

因为各频率点信号的采样点为复值，所以必须采用复数域下的目标函数。由于峭度相较负熵、互信息等目标函数避免了非线性函数及概率密度函数的选取，所需源信号先验知识较少，本文采用复数域峭度作为目标函数。对于超高斯及亚高斯信号而言，峭度分别为正和负，为了实现不同分布信号的盲分离，需要取峭度的绝对值。由式(11)可知，分离矩阵W(f)是旋转角度θ的函数，所以构造目标函数为

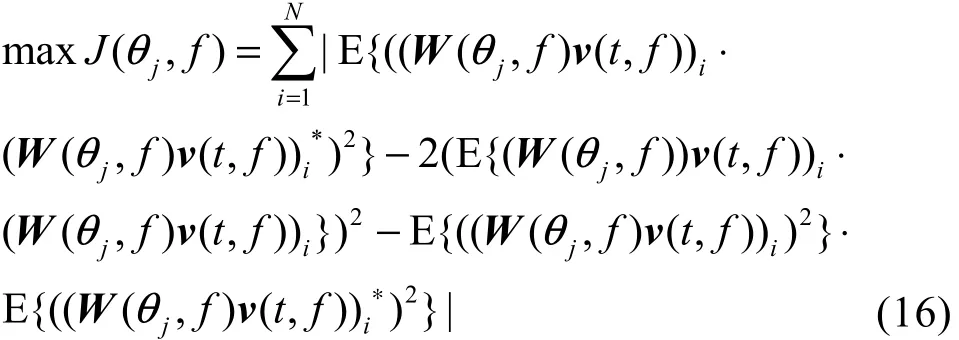
其中，N为信号的路数，上标∗为取共轭，E为取均值，⋅为取绝对值。用蝙蝠算法优化旋转角度使目标函数取得极大值，从而完成各频率点的线性瞬时混合复值信号盲分离。

进一步，需要消除各频率点分离信号存在的顺序模糊性及比例模糊性。时域下分离信号幅度的比例伸缩及顺序错位并不影响对分离结果的理解，频域下则会影响分离效果。频域下各频率点的顺序错位会导致相邻频率点来自不同信号的子信号重新混合，无法实现最终的分离。本文依据相邻频率点来自同一源信号的分离信号之间幅度相关性大于来自不同源信号的分离信号之间的幅度相关性这一准则进行排序，2个相邻频率点的复值分离信号ym(f)和 yl( f+ 1)之间的幅度相关系数如下

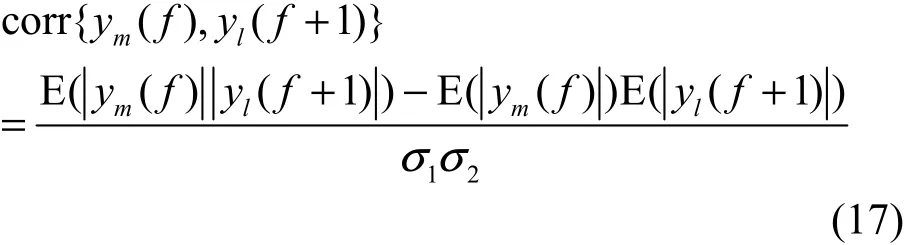
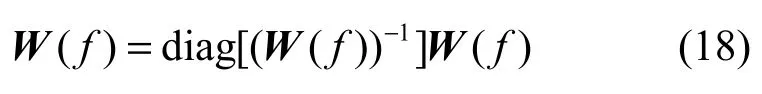
其中，diag表示对角化。

4.3 算法步骤

基于复 Givens矩阵与蝙蝠优化的卷积盲分离算法具体步骤如下。

步骤1 将时域卷积混合信号经STFT转换为各个频率点的线性瞬时混合复值信号。

步骤 2 对各频率点的混合信号进行中心化和白化预处理。

步骤 3 根据信号路数，初始化各频率点搜索种群，确定蝙蝠数量及维数，搜索范围为[−π,π]，每个蝙蝠的位置代表分离矩阵的一个可能解，由复Givens矩阵连乘的形式表示。

步骤4 依据式(4)，以每个蝙蝠的位置求得各频率点分离信号，采用式(16)作为蝙蝠算法的适应度函数，求得初始条件下各频率点最佳蝙蝠。

步骤5 对各参量进行更新，依据步骤4求得每次迭代的各频率点最佳蝙蝠。

步骤 6 若达到最大迭代次数，输出各频率点最佳蝙蝠即为分离矩阵W(f)，否则重复步骤5。

步骤7 依据式(4)求得各频率点分离信号。

步骤 8 依据式(17)和式(18)解决各频率点求得分离信号的顺序模糊性和比例模糊性。

步骤9 经ISTFT恢复时域中分离信号，即源信号的估计。

5 仿真实验与分析

为了验证本文算法的有效性，进行2组实验。实验1为不同分布复值线性瞬时混合信号盲分离，实验2为语音卷积混合信号盲分离。实验1采用卷积混合信号在各频率点进行盲分离的算法，为实验2提供基础。通过将其他一些方法作为对照，分别测试本文算法对不同分布复值线性瞬时混合信号盲分离及卷积混合信号盲分离的效果。

5.1 不同分布复值线性瞬时混合信号盲分离

本实验采用3路服从不同分布的复值信号作为源信号。s1( t)为 BPSK信号，s2( t)为实部服从Poisson分布、虚部服从 Gamma分布的信号，s3( t) =r( t) [cos(ϕ( t) ) + isin(ϕ(t ))]，r( t)服从 Poisson分布，ϕ(t)在[−π,π]之间随机产生。信号的采样点数为5 000。

判断源信号的分布特性，依据复数域峭度。峭度值为正，信号服从超高斯分布；峭度值为负，信号服从亚高斯分布。复数域峭度的定义如下[10]

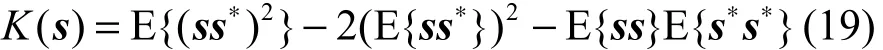
其中，s表示复值信号，∗表示取共轭，E表示取均值。判断复值源信号的正则性，依据伪协方差矩阵Css，若 Css=0则为正则信号，反之，则为非正则信号。Css的定义如下

其中，T表示转置， m = E(sr) + jE(si)表示信号的均值。s1( t)的峭度值 K( s1( t)) =−2 < 0，伪协方差矩阵 Css=1，为服从亚高斯分布的非正则信号；s2( t)的峭度值 K( s2( t))= 10.522 7 > 0，伪协方差矩阵Css=0.29，为服从超高斯分布的非正则信号；s3( t)的峭度值 K( s3( t)) = 22.9843 > 0，伪协方差矩阵Css=0，为服从超高斯分布的正则信号。

所用3阶复混合矩阵 A=[1+ 2i,3+ i,2+ i;4+2i,2 + i,1 + 0.5i;3 + i,9 + 2i,2 + 2i]。实验中分别采用复数域下的快速固定点（C-FastICA）算法[7]、基于峭度的梯度（KM-G）算法[10]、联合块对角化（JADE）算法[18]以及本文算法进行对照仿真。

各算法参数设置如下。

KM-G算法：步长0.1，分离矩阵初值向量为[0,1]内均匀分布的随机数。

JADE算法：累积量矩阵的个数为3。

本文算法：蝙蝠的个数为 20，维数为 12，搜索范围[−π,π]，脉冲音强及脉冲频率均为 0.5，频率范围[0,2]。

图2 采用不同算法分离不同分布线性瞬时混合复值信号所得分离信号星座图

因盲分离的目的为使所获取的分离信号与源信号之间的相似程度尽可能高，为了更加直观地对其进行比较，图2给出了源信号及分别采用上述4种算法所得分离信号的星座图。

C-FastICA算法不能实现正则与非正则混合信号的分离，且受非线性函数选取的影响，未恢复源信号。KM-G算法、JADE算法及本文算法对源信号的先验知识要求较少，均可实现信号分离。为了客观说明算法分离性能，本文采用相关系数的模ζ作为评价指标。因为信号采样点均为复数，相关系数为复值，所以取模。相关系数的模定义为[19]

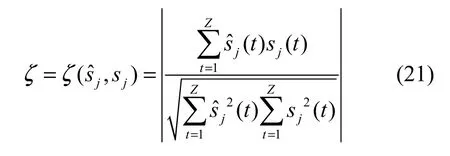
其中，Z为信号的采样点数，sj表示第j路源信号，sˆj表示分离信号中第 j路源信号 sj的估计，|·|表示求模运算。ζ取值为0～1，取值为0时说明两信号互不相关，取值越大，则两信号的相关程度越大。表1列出了KM-G算法、JADE算法及本文算法所得分离信号相关系数的模。实验结果数据为 20次仿真的平均值。

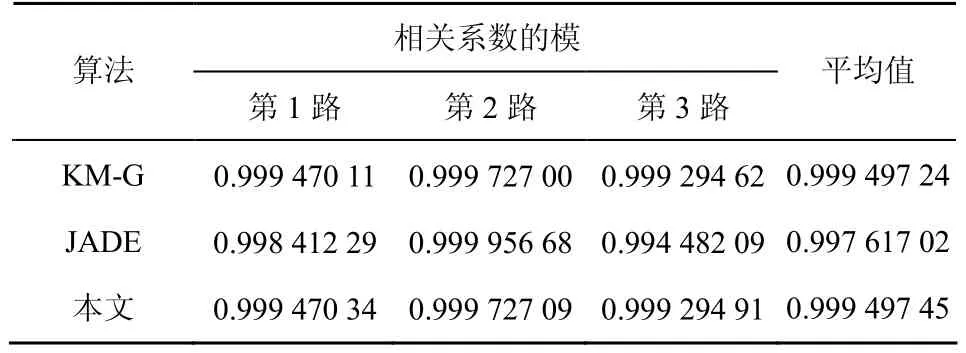
表1 采用不同算法用于3路不同分布复值信号盲分离所得相关系数的模

通过对相关系数的模分析可知，本文算法所求得信号相关系数的模均在0.999 2以上，可以精确恢复源信号。与KM-G算法及JADE算法对比，提高了分离精度。综上，本文算法可以实现不同分布线性瞬时混合复值信号盲分离，并且效果很好。因卷积混合信号转化到频域后，各频率点上为线性瞬时混合复值信号，此实验为实验2提供基础。

5.2 语音卷积混合信号盲分离

本实验采用来自NTT通信科学实验室Hiroshi Sawada的主页所提供的3路语音信号作为源信号注注1：http：//www.kecl.ntt.co.jp/icl/signal/sawada/demo/bss2to4/index.html。1。信号采样频率为8 kHz，采样周期为 1.25× 10−4s，分辨率16位/采样点，即量化位数为16，每个采样点由16位二进制数组成，数值介于-32 768和32 767之间，然后将量化电平值转为-1和1区间，得信号采样点图，信号长度为56 000。3路语音源信号的峭 度 值 分 别 为 4.5241× 10−6、 5.5768× 10−6、2.9481× 10−6，均服从超高斯分布。通过如下所示的9个5阶滤波器对源信号进行卷积混合

作为对照实验，本文分别在时域及频域进行卷积混合盲分离的求解。时域中利用快速固定点（Fast-ICA）算法[20]进行求解。频域中分别利用下述方法进行求解：直接应用于频域卷积混合盲分离的独立矢量分析（IVA）算法[8]、实验1中所采用的应用于各个频率点的复值盲分离算法（C-FastICA算法[7]、KM-G 算法[10]、JADE 算法[18]以及本文算法）。其中，频域算法所采用的STFT的阶数为1 024，窗长为256，重叠比率为，时频变化后共513个频率点，每个频率点信号的采样点数为878。

各算法参数设置如下。

Fast-ICA算法：分离矩阵初值向量为[0,1]内均匀分布的随机数。

IVA算法：步长 0.1，概率密度函数选用多维Laplace分布即分离矩阵初值为单位阵。

KM-G算法：步长0.1，分离矩阵初值向量为[0,1]内均匀分布的随机数。

JADE算法：累积量矩阵的个数为3。

本文算法：蝙蝠的个数为 20，维数为 12，搜索范围为[−π,π]，脉冲音强及脉冲频率均为 0.5，频率范围为[0,2]。

为了更加直观地对各算法所得分离信号与源信号进行比较，图3给出了源信号及各个算法所得分离信号波形图。

图3 采用不同算法分离3路卷积混合信号所得分离信号

Fast-ICA算法为在时域解决线性瞬时混合盲分离的方法，未考虑信号的衰减和时延，并不能解决卷积混合盲分离问题。其他算法为卷积混合盲分离的频域求解算法，IVA算法将每个信号的所有频点分量视为一个整体进行分离信号的求解，图3(d)～图3(g)所示算法分别在各个频点进行复值线性瞬时混合盲分离，图3(c)～图3(g)所示算法均可实现源信号的恢复。为了客观说明各算法分离性能，在实验1的基础上增加重构信噪比这一评价指标。因实验1为复数域下线性瞬时混合盲分离，信号采样值为复数，不适合计算所以并未采用这一评价指标定义为[21]

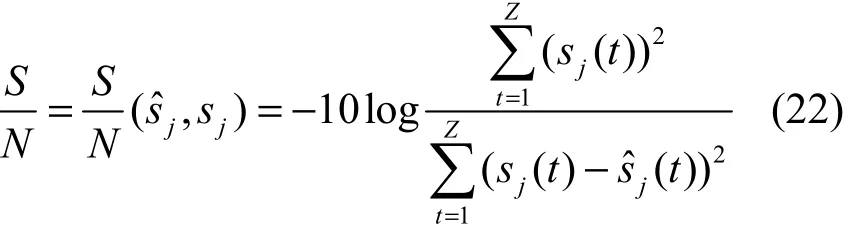
其中，Z为信号的采样点数，sj表示第j路源信号，sˆ表示分离信号中第j路源信号s的估计。的值

j

j越大，表示分离信号与源信号之间的误差越小，分离效果越好。表2分别列出了上述6种算法所得分离信号的相关系数绝对值及重构信噪比，因时域下信号采样点为实数，所以对相关系数取绝对值。实验结果数据为20次仿真的平均值。

IVA算法、C-FastICA算法及KM-G算法需要选取概率密度函数、非线性函数或步长等参量，而且均易受分离矩阵初值的影响，在一定程度上限制了分离性能。本文算法所求得分离信号相关系数绝对值的均值达到了 0.98以上，重构信噪比的均值达到15 dB以上，源信号恢复效果很好，较其他算法有所提升。虽然KM-G算法与本文算法的分离性能指标接近，但KM-G算法受步长选取的影响较大，算法的收敛速度与稳定性难以同时满足，而且分离矩阵初值向量的选取也会影响其分离性能。综上，本文算法相较其他一些算法，具有很大优越性。

6 算法复杂度分析

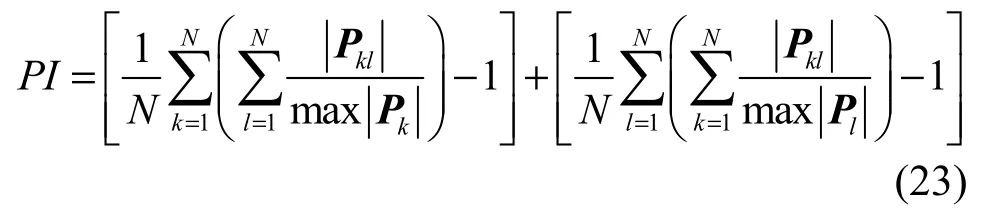
为了进一步分析算法的复杂度，作出了不同算法PI收敛曲线。PI的定义为[22]其中，N指信号的路数表示求模运算。PI值越小，分离的效果越好。因JADE算法不涉及迭代运算，图 4给出了本文算法及 KM-G算法的PI收敛曲线。

图4 本文算法及KM-G算法的PI收敛曲线

表2 采用不同算法用于3路卷积混合信号盲分离所得相关系数绝对值及重构信噪比

由图4可知，本文算法比KM-G算法的收敛速度更快，仅在第12次迭代时PI值收敛于0.082 4，PI收敛值比KM-G算法的PI收敛值更小，分离效果更好。为了进一步对算法进行比较，表3给出了当迭代次数为12时，本文算法及KM-G算法所得分离信号相关系数的模。

表3 本文算法及KM-G算法所得分离信号相关系数的模

当迭代次数为12时，KM-G算法因未收敛，所得分离信号性能不高，较表1有所降低。通过对比，本文算法所得分离信号相关系数的模较KM-G算法有较大提升。为了多方面比较算法性能，表4给出了当满足收敛条件时各算法的运行时间。

各算法的运行时间很接近，但JADE算法的分离性能并不高，KM-G算法受步长及分离矩阵初值向量的选取影响较大。步长的选取使算法的收敛速度与稳定性难以同时满足，不易确定。虽然随步长的增加，算法的收敛速度更快，但分离效果有所降低，而随步长的减小，算法的收敛速度明显减慢，运行时间也会显著增加。分离矩阵初值向量选取不当也会降低算法性能。本文算法不受步长及分离矩阵初值向量选取的影响，而且分离性能较其他算法有所提升。

此外，为了缩短群智能算法的运行时间，多种GPU并行算法的方案被提出[23～26]，时间至少可减少为原来的，效果很理想。本文所用蝙蝠算法也是群智能算法的一种，可以利用 GPU并行算法来缩减运算时间，将作为下一步的研究方向。

7 结束语

本文提出了一种基于复 Givens矩阵与蝙蝠优化的频域卷积盲分离算法。依据QR分解理论，将分离矩阵用复Givens矩阵表示，然后利用蝙蝠算法优化求解旋转角度完成各频率点线性瞬时混合复值信号盲分离。复Givens矩阵的使用减少了待求解的未知参数个数，降低了算法求解难度和计算量，而且保证了分离矩阵的正交性，提高了计算精度。利用蝙蝠算法取代传统的梯度算法优化复 Givens矩阵中旋转角度，避免了步长及分离矩阵迭代初值的选取，全局收敛性能更好。此外，在求解过程中避免了非线性函数及概率密度函数的选用，对源信号的先验知识要求较少，可以分离服从多种分布的信号。仿真结果表明，本文算法相较其他一些算法提高了分离效果。

[1] YANG Z Y, XIANG Y, RONG Y, et al. A convex geometry-based blind source separation method for separating nonnegtive sources[J].IEEE Transactions on Neural Networks and Learning Systems, 2015,26(8)： 1635-1644.

[2] RIVET B. Source separation of multimodal data： a second-order approach based on a constrained joint block decomposition of covariance matrices[J]. IEEE Signal Processing Letters, 2015, 22(6)： 681-685.

[3] FU G S, PHLYPO R, ANDERSON M, et al. Blind source separation by entropy rate minimization[J]. IEEE Transactions on Signal Processing, 2014, 62(16)： 4245-4255.

[4] OUEDRAOGO W S B, SOULOUMIAC A, JAIDANE M, et al.Non-negative blind source separation algorithm based on minimum aperture simplicial cone[J]. IEEE Transactions on Signal Processing,2014, 62(2)： 376-389.

[5] WON Y G, LEE S Y. Convolutive blind signal separation by estimating mixing channels in time domain[J]. Electronics Letters, 2008,44(21)： 1277-1279.

[6] CASTELLA M, RHIOUI S, MOREAU E, et al. Quadratic higher order criteria for iterative blind separation of a MIMO convolutive mixture of sources[J]. IEEE Transactions on Signal Processing, 2007,55(1)： 218-232.

[7] BINGHAM E, HYVARIEN A. A fast fixed-point algorithm for independent component analysis of complex valued signals[J]. International Journal of Neural Systems, 2000, 10(1)： 1-15.

[8] LEE I, KIM T, LEE T W. Fast fixed-point independent vector analysis algorithms for convolutive blind source separation[J]. Signal Processing, 2007, 87(8)： 1859-1871.

[9] CARDOSO J F. Equivariant adaptive source separation[J]. IEEE Transactions on Signal Processing, 1996, 44(12)： 3017-3029.

[10] LI H, ADALI T. A class of complex ICA algorithms based on the kurtosis cost function[J]. IEEE Transactions on Neural Networks,2008, 19(3)： 408-420.

[11] YANG X S. A new metaheuristic bat-inspired algorithm[C]// International Workshop on Nature Inspired Cooperative Strategies for Optimization. Granada, c2010： 65-74.

[12] PREMKUMAR K, MANIKANDAN B V. Speed control of brushless DC motor using bat algorithm optimized adaptive neuro-fuzzy inference system[J]. Applied Soft Computing, 2015, 32： 403-419.

[13] NIKNAM T, BAVAFA F, AZIZIPANAH-ABARGHOOEE R. New self-adaptive bat-inspired algorithm for unit commitment problem[J].IET Science Measurement & Technology, 2014, 8(6)： 505-517.

[14] JADDI N S, ABDULLAH S, HAMDAN A R. Optimization of neural network model using modified bat-inspired algorithm[J]. Applied Soft Computing, 2015, 37： 71-86.

[15] 覃和仁, 谢胜利. 基于 QR分解与罚函数方法的盲分离算法[J]. 计算机工程, 2003, 29(17)： 55-57.QIN H R, XIE S L. Blind separation algorithm based on QR decomposition and penalty function[J]. Computer Engineering, 2003, 29(17)：55-57.

[16] 杜鹃, 冯思臣. 复矩阵的Givens变换及其QR分解[J]. 成都理工大学学报(自然科学版), 2011, 38(6)： 693-695.DU J, FENG S C. Givens transformation and QR factorization of complex matrix[J]. Journal of Chengdu University of Technology (Science&Technology Edition), 2011, 38(6)： 693-695.

[17] MATSUOKA K, NAKASHIMA S. Minimal distortion principle for blind source separation[C]//International Workshop on Independent Component Analysis and Blind Signal Separation. Osaka, c2001： 722-727.

[18] CARDOSO J F, SOULOUMIAC A. Blind beamforming for non-Gaussian signals[J]. IEE Proceedings F-Radar and Signal Processing, 1993, 140(6)： 362-370.

[19] 陈晓军, 成昊, 唐斌. 基于ICA的雷达信号欠定盲分离算法[J]. 电子与信息学报, 2010, 32(4)： 919-924.CHEN X J, CHENG H, TANG B. Underdetermined blind radar signal separation based on ICA[J]. Journal of Electronics & Information Technology, 2010, 32(4)： 919-924.

[20] HYVARINEN A. Fast and robust fixed-point algorithms for independent component analysis[J]. IEEE Transactions on Neural Networks, 1999, 10(3)： 626-634.

[21] 陈雷, 张立毅, 郭艳菊, 等. 基于时间可预测性的差分搜索盲信号分离算法[J]. 通信学报, 2014, 35(6)：117-125.CHEN L, ZHANG L Y, GUO Y J, et al. Blind signal separation algorithm based on temporal predictability and differential search algorithm[J]. Journal on Communications, 2014, 35(6)： 117-125.

[22] CICHOCKI A, AMARI S. Adaptive blind signal and image processing：learning algorithms and applications[M]. New York： Wiley, 2002.

[23] DALI N, BOUAMAMA S. GPU-PSO： parallel particle swarm optimization approaches on graphical unit for constraint reasoning： case of max-CSPs[C]//International Conference on Knowledge Based on Intelligent Information and Engineering System. Singapore, c2015：1070-1080.

[24] OUYANG A, Tang Z, ZHOU X, et al. Parallel hybrid PSO with CUDA for 1D heat conduction equation[J]. Computer & Fluids, 2015, 110： 198-210.

[25] TOUTOUH J, ALBA E. Parallel swarm intelligence for VANETs optimization[C]//International Conferrence on P2P, Parallel, Grid,Cloud and Internet Computing. Victoria, Spain, c2012： 285-290.

[26] SILVA E H M, BASTOS FILHO C J A. PSO efficient implementation on GPUs using low latency memory[J]. IEEE Latin America Transactions, 2015, 13(5)： 1619-1624.

Convolutive blind separation algorithm based on complex Givens matrix and bat optimization

JIA Zhi-cheng1, HAN Da-wei1, CHEN Lei2,3, GUO Yan-ju1, XU Hao-da1
(1. Institute of Electronic Information Engineering, Hebei University of Technology, Tianjin 300401, China;2. Institute of Precision Instrument and Optoelectronics Engineering, Tianjin University , Tianjin 300072, China;3. Institute of Information Engineering, Tianjin University of Commerce, Tianjin 300134, China)

For the limitations such as many unknown parameters, the separation accuracy was easily influenced by initial value of separation matrix in traditional convolutive blind separation, a kind of frequency method based on complex Givens matrix and bat optimization was proposed. The algorithm used a series of complex Givens matrices to denote separation matrix, it reduced unknown parameters, decreased the difficulty and the amount of calculations as a result. Besides, the algorithm utilized bat algorithm instead of conventional gradient algorithm to optimize rotation angles and completed the separation of complex linear instantaneous mixing signals at each frequency point, the use of bat algorithm made the optimization ability better. In addition, little prior information was needed and signals following various distributions could be separated. Simulation results show that the proposed method can realize convolutive blind separation efficiently.

blind separation, convolutive mixtures, bat algorithm, complex Givens matrix

s: The National Natural Science Foundation of China (No. 61401307), The China Postdoctoral Science Foundation(No.2014M561184), Tianjin Research Program of Application Foundation and Advanced Technology(No. 15JCYBJC17100)

TN911.7

A

10.11959/j.issn.1000-436x.2016138

2016-01-23；

2016-04-24

陈雷，chenleitjcu@139.com

国家自然科学基金资助项目（No.61401307）；中国博士后科学基金资助项目（No.2014M561184）；天津应用基础与前沿技术研究计划基金资助项目（No.15JCYBJC17100）

贾志成（1957-），男，黑龙江齐齐哈尔人，河北工业大学教授、硕士生导师，主要研究方向为智能算法和盲源分离等。

韩大伟（1990-），女，河北廊坊人，河北工业大学硕士生，主要研究方向为盲信号处理。

陈雷（1980-），男，河北唐山人，博士，天津商业大学副教授，主要研究方向为盲信号处理、仿生智能计算等。

郭艳菊（1980-），女，河北邢台人，河北工业大学讲师，主要研究方向为盲信号处理、高光谱图像处理。

许浩达（1990-），男，河北保定人，河北工业大学硕士生，主要研究方向为基于DSP的盲信号处理、智能算法等。