考虑电源特性的逆变器控制参数选择
周欐颜,邢建春
(解放军理工大学 国防工程学院,江苏 南京210007)
考虑电源特性的逆变器控制参数选择
周欐颜,邢建春
(解放军理工大学 国防工程学院,江苏 南京210007)
可再生能源渗透率较高的孤立微电网中,储能系统作为备用电源,其控制对系统电压和频率的稳定性有着重要的影响。建立了包括储能模型在内的微电网数学模型,综合考虑储能状态及逆变器控制参数对系统的影响,深入研究分析了控制器参数影响系统稳定性的规律,最后通过仿真实验验证了结果的正确性。
微电网;电源特性;逆变器控制;稳定性分析;控制参数
0 引言
孤立型微电网常含有光伏、风力、柴油发电机组及电池储能等大量通过逆变器并网的分布式电源,一般依靠储能系统维持其电压和频率的稳定性。而且该类系统在孤岛运行模式下的动态响应特性与并网模式时存在很大的差异[1],其逆变器的控制方法与策略是整个系统稳定、高效、经济运行的关键。逆变器等电力电子装置在提高系统运行及控制灵活性的同时,存在系统惯量较小,受到扰动易发生振荡失稳的缺陷,而且在电源参数变化较大及充/放电的不同状态下系统稳定控制难度变得更高[2]。
稳定性作为电网可靠运行的判断条件之一,已经有不少学者对它进行了分析研究。一类文献专门针对单一逆变器的控制方式及控制方式之间的切换对小信号稳定性进行了分析[3-4],简化了多逆变器并网等其他因素的影响;另一类文献建立了包括微电源及负荷在内的完整的微电网模型,进行动态的小信号稳定性分析,但是往往会把储能等电源模型等效为理想电源模型[5-8]。
本文建立了包括蓄电池数学模型在内的微电网小信号模型,通过对这类系统状态矩阵进行特征值分析,分别研究了储能状态和逆变器PI控制参数对系统稳定性的综合影响,深入研究分析了控制器参数影响系统稳定性的规律,最后通过仿真实验验证了结果的正确性。
1 储能系统数学模型
如图1所示,一般的储能逆变系统由三相DC-AC逆变器负责交直流之间的转换,通过不同控制策略满足微电网的供电需求,保障较高的电能质量。

图1 储能逆变系统结构图
1.1蓄电池组
根据蓄电池的通用等效电路模型[9]建立储能单元的数学方程,如式(1)所示。忽略蓄电池内阻及容量在充放电过程中的变化,忽略蓄电池温度及自放电特性的影响。在该模型中,充放电状态(State of Charge,SOC)是唯一的状态变量。
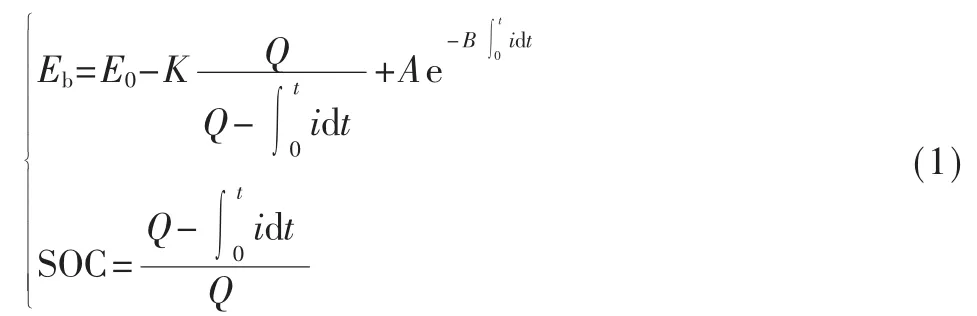
式中,E0为开路电压,K为极化电压,Q为电池容量,A、B为蓄电池特性常数,i为放电电压。
1.2DC-DC-AC逆变系统
首先,DC-DC变换器的平均数学模型如下所示。

式中,udc为直流侧电容电压,i0为输入电流,Lb为平波电抗,Cdc为直流侧电容,Rb为蓄电池等效内阻,d′为开关占空比,dd、dq为两相旋转坐标系下单极性二值逻辑开关函数。
1.3逆变器控制系统
逆变器的控制方法为下垂控制法,并通过电压电流双环控制器稳定逆变器的输出电压和电流。下垂控制的控制方程如式(3)、式(4)所示。
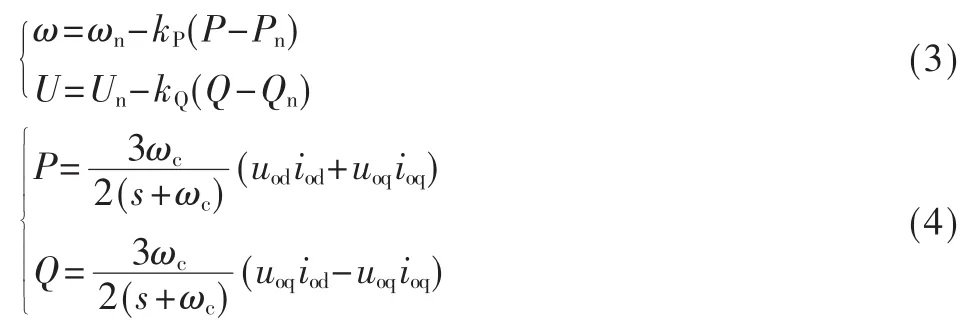
其中,kP、kQ分别为频率和电压下垂系数,ωn、Un、ω、U分别为电网角频率和电压的额定值与参考值,Pn、Qn、P、Q分别为输出有功功率及无功功率的额定值与平均值,ωc为低通滤波器的截止频率。
电压电流双环控制器通常对控制进行dq轴分量解耦,以实现更精准的控制[10],电压环和电流环控制方程分别如式(5)和式(6)所示。

其中,kVP、kVI为电压环 PI控制器的比例和积分参数,kCP、kCI为电压环 PI控制器的比例和积分参数。
1.4储能逆变系统小信号状态空间模型
式(1)~式(6)描述了整个储能逆变系统的重要部分,将这些方程线性化之后再建立LC滤波器、网络以及负荷的线性方程就可以得到整个系统的小信号模型。为方便计算,补充以下两个变量关系:
(1)频率较高(4~10 kHz)时,开关部分的动态影响可以被忽略,可以认为

2 小信号稳定性分析
为研究储能状态对逆变系统小信号稳定性的影响,首先求解出系统的稳态运行参数。针对大容量、大功率、高电压等级的储能单元向电网供电的情况,建立系统的模型。根据储能SOC的不同,利用已知的控制参数和电路参数(见表1)仿真计算出表2所示的不同SOC下系统的稳态运行参数。
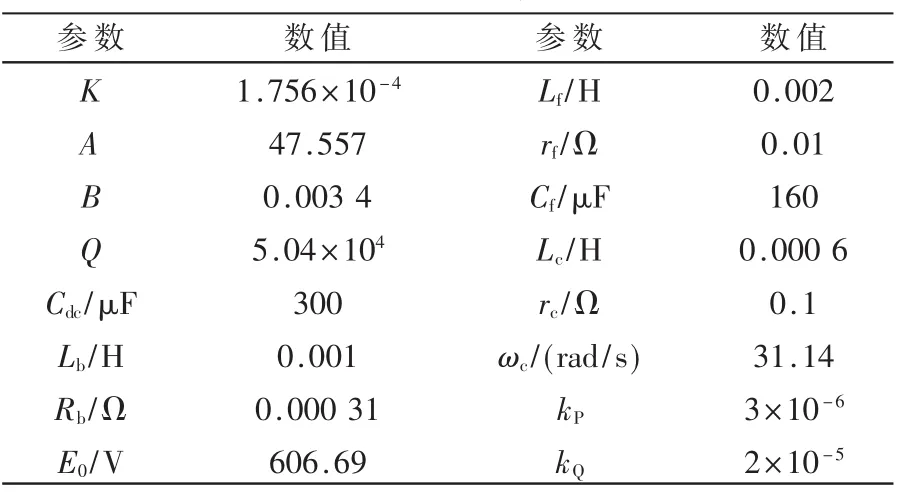
表1 系统参数
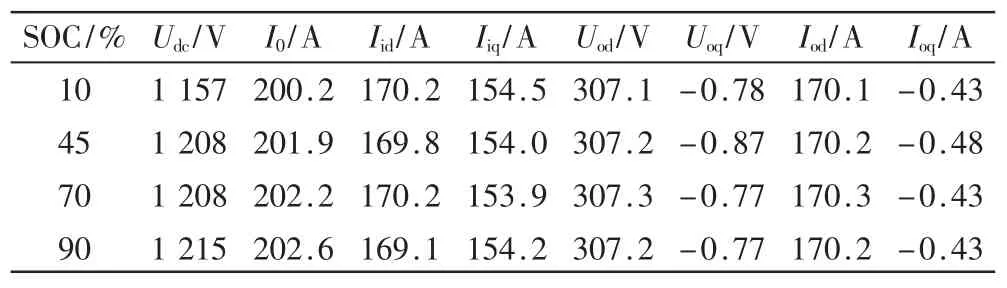
表2 不同SOC下系统的稳态参数
依据稳态运行参数的变化趋势,取SOC=10%,SOC= 90%这两组数据进行接下来的小信号稳定性分析。特征值分析法是通过计算系统状态矩阵的特征值分析系统的全部振荡模式的方法,本文将采用特征值分析法研究逆变器控制器参数和储能状态对逆变系统小信号稳定性的影响。
2.1SOC给定时
电压环及电流环PI控制器参数初值分别取 SOC= 90%,kVI=10,kVP=20,kCI=20,kCP=10。根据特征值分析法,对系统状态矩阵求取特征值,并对14个特征值进行编号。状态矩阵特征值的定义,可知特征值的实部表示系统的阻尼,虚部表示振荡的频率。由于靠近虚轴的特征值对应的系统阻尼比较小,容易引起系统的不稳定,所以低阻尼特征值的根轨迹特性是本文研究重点。本文通过改变变量法逐个分析每个控制参数的主特征根轨迹,研究该控制参数对系统小信号稳定性的影响。4个参数分别变化时的主特征根轨迹如图2~图5所示。
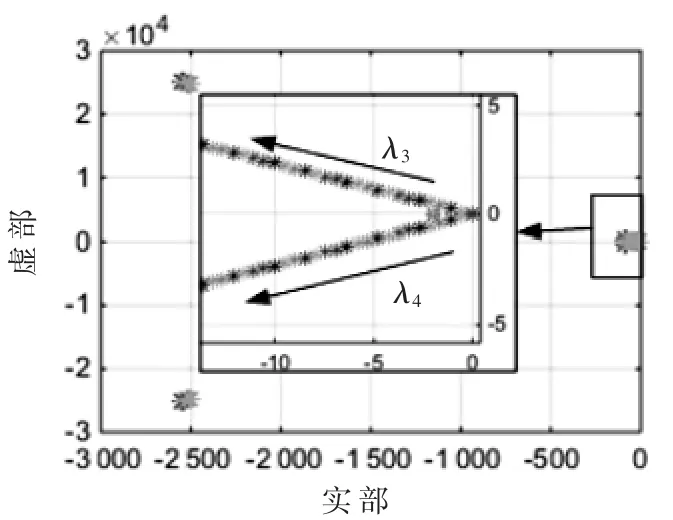
图2 kVI变化时主特征值轨迹(kVP=20,kCI=10,kCP=20,SOC=90%,0<kVI≤300)
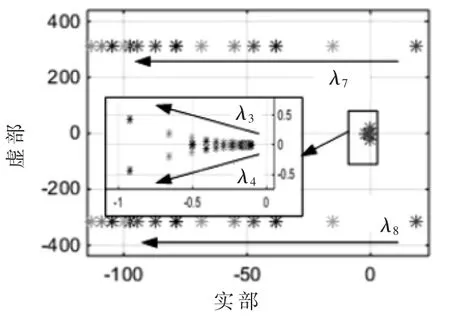
图3 kVP变化时主特征值轨迹(kVI=10,kCI=10,kCP=20,SOC=90%,0<kVP≤150)

图4 kCI变化时主特征值轨迹(kVI=10,kVP=20,kCP=20,SOC=90%,0<kCI≤200)

图5 kCP变化时主特征值轨迹(kVI=10,kVP=20,kCI=10,SOC=90%,0<kCP≤100)
通过比较分析图2~图5,可以得出以下的一些结论:
(1)逆变器控制参数对系统小信号稳定性的影响主要由 4对特征值 λ1、λ3、λ5、λ7体现(由于特征值的对称性,省略实轴以下的部分)。
(2)由于 4个参数之间的相互影响,某个参数满足系统稳定性的取值范围会随着其他3个参数的变化而变化,但这个参数的变化对特征值造成的影响是相似的。所以当 λ7不满足稳定性要求时可以增大 kVP的值;当 λ5不满足稳定性要求时可以减小 kCI的值;当 λ3不满足稳定性要求时可以增大kVP的值或减小kCI的值;当λ1不满足稳定性要求时可以减小 kCP的值。
(3)参数kVP的取值对系统小信号稳定性的影响较大,当kVP过小时,系统会不稳定。因为当kCP由0取到100时,特征根实部的变化范围只有 0.01,所以 kCP对系统稳定性影响不大。
2.2SOC变化时
当控制器参数取 kVI=20,kVP=250,kCI=5,kCP=40,SOC设定值分别10%,45%,90%时,除最靠近虚轴的特征值λ1、λ2之外,其他特征值基本不变。特征值λ1、λ2的分布图如图6所示,从中可以看出储能充足时,系统的小信号稳定性更好,应当根据SOC偏低时的稳定运行条件整定PI控制器的参数,以满足系统运行要求。根据2.1节总结的规律,调节控制器参数的取值可以减小储能状态SOC对系统性能的影响。在系统小信号稳定性不是很好的情况下,控制器参数的整定需要考虑电源输出特性变化带来的影响。

图6 SOC变化时主特征值λ1、λ2的分布图
3 仿真验证
本文在 MATLAB/Simulink软件平台上建立了大容量、高功率的储能逆变系统模型进行仿真验证。仿真开始时设置负荷为 100 kW 和 20 kvar,在仿真时间为 3 s时增加有功负荷 25 kW,无功负荷 5 kvar,电源、电路及部分控制器参数如表1所示。
依据2.2节的分析结果,若是当 SOC为10%时,系统能满足稳定性要求,则储能更加充足时,系统依然能保持稳定。依据2.1节的分析结果,适当增大kVP的取值或减小kCI的取值可以调整系统小信号稳定性。为验证这个规律,选取3组不同的控制参数,分别运行仿真程序,观察系统输出的电压及功率曲线。3组控制参数分别为:(1)kVI=20,kVP=250,kCI=5,kCP=40;(2)kVI=20,kVP=200,kCI=20,kCP=40;(3)kVI=20,kVP=200,kCI=5,kCP=40。仿真结果如图7所示,3组参数的仿真结果分别以实线、点线、虚线表示,各组参数的取值按 kVI,kVP,kCI,kCP的顺序标注在图例中。

图7 仿真结果
由图7可知,3组控制参数都能满足逆变器控制要求,即维持输出电压稳定的情况下满足负荷功率需求。其中,第(1)组控制参数的控制效果最好,输出功率曲线及输出电压曲线的波动都是最小的。对比这3组控制参数,当 kVP从 200变化为 250时(第(1)组和第(3)组)和当kCI从20变化为 5时(第(2)组和第(3)组),系统的稳定性都有所改善,与特征值分析得到的结论相符。双环控制器的 PI控制器参数选取第(1)组控制参数时,能够在满足功率负荷控制要求的基础上,降低电源特性的影响,优化电压幅值控制效果。
4 小结
本文建立了含蓄电池组通用数学模型的储能逆变系统的小信号模型,通过小信号稳定性分析方法,研究了储能状态及电压双环控制器的PI参数对微电网稳定性的影响,得出了PI参数整定的3条规律:
(1)PI参数整定时应当考虑储能不充足时的稳定性;
(2)电压环的比例参数 kVP、积分参数 kVI、电流环的积分参数 kCI对系统小信号稳定性影响较大;
(3)可以适当增加 kVP的取值或减小 kCI的取值来增强系统稳定性。
在MATLAB/Simulink中建立了储能逆变系统模型,验证了PI控制参数影响稳定性的规律,为传统双环控制控制参数的设计提供参考。
[1]陈建斌,付超,陈柔伊,等.含多种分布式电源的微网系统孤岛运行安全稳定性[J].南方电网技术,2013,7(4):71-74.
[2]金一丁,宋强,刘文华.电池储能系统的非线性控制器[J].电力系统自动化,2009,33(7):75-80.
[3]范元亮,苗逸群.基于下垂控制结构微网小扰动稳定性分析[J].电力系统保护与控制,2012,40 (4):1-7.
[4]郑竞宏,李兴旺,王燕廷,等.微电网切换至孤岛运行时的小信号稳定性分析[J].电力系统自动化,2012,36 (15):25-32.
[5]张建华,苏玲,刘若溪,等.逆变型分布式电源微网小信号稳定性动态建模分析[J].电力系统自动化,2010,34 (22):97-102.
[6]周丹,赵波,张雪松,等.并网运行的储能逆变器小信号稳定性分析[J].浙江电力,2014,33(1):1-4,29.
[7]李洋,张辉,苏冰,等.含多微源的微电网离网运行小信号稳定性分析[J].电力自动化设备,2015,35(1):159-164.
[8]杨俊虎,韩肖清,曹增杰,等.基于逆变器下垂控制的微电网动态性能分析[J].南方电网技术,2012,6(4):48-52.
[9]杨勇.太阳能系统用铅酸蓄电池综述[J].蓄电池,2009 (2):51-57.
[10]王成山,肖朝霞,王守相.微网综合控制与分析[J].电力系统自动化,2008,32(7):98-103.
Control parameter selection of micro-grid considering energy storage characteristic
Zhou Liyan,Xing Jianchun
(PLA University of Science and Technology,Nanjing 210007,China)
The control of energy storage system has important influence on the stability of the voltage and frequency of the isolated micro-grid system.In this paper,a small-signal model of micro-grid is established,especially including energy storage model. Based on the existing small signal analysis,the influence of the energy storage state and the control parameters of the inverter on the stability of islanded micro-grid is analyzed,and the rule of those influences is summarized.The simulation results show that the system has strong adaptability to load mutation and energy storage state fluctuation with controller parameters determined according to the rule.
microgird;energy storage characteristic;inverter control;stability analysis;control parameters
TM464
A
10.16157/j.issn.0258-7998.2016.05.038
2016-01-27)
周欐颜(1991-),女,硕士研究生,主要研究方向:微电网综合控制。
邢建春(1964-),男,教授,博士生导师,主要研究方向:复杂系统智能化等。
中文引用格式:周欐颜,邢建春.考虑电源特性的逆变器控制参数选择[J].电子技术应用,2016,42(5):139-142.
英文引用格式:Zhou Liyan,Xing Jianchun.Control parameter selection of micro-grid considering energy storage characteristic[J]. Application of Electronic Technique,2016,42(5):139-142.

