基于最短路径特征的社团发现算法*

杨艳新，熊小峰，乐光学

（1.江西理工大学 理学院，江西 赣州 341000；2.嘉兴学院 数理与信息工程学院，浙江 嘉兴 314000）

基于最短路径特征的社团发现算法*

杨艳新1,2，熊小峰1，乐光学1,2

（1.江西理工大学 理学院，江西 赣州 341000；2.嘉兴学院 数理与信息工程学院，浙江 嘉兴 314000）

为了准确快速地挖掘社团结构，提出基于最短路径特征的社团发现算法SPCDA（Shortest Path feature community discovery algorithm）。该算法是基于最短路径特征的启发，根据最短路径数目的特征计算每个节点的中介系数而获取社团中心，并由其长度的特征计算节点之间的相似度值。然后，取所有节点的平均相似度值作为划分社团的阈值，构成类似于聚类的模型。最后，将与社团中心的相似度值大于阈值的节点进行归类，按照此过程不断迭代，至节点集为空。将该算法应用于人工合成网络和两个经典的真实社会网络，并与GN算法和LPA算法进行比较，结果证明SPCDA算法能够准确、快速地挖掘隐藏的社团结构。

社团结构；最短路径；中介系数；相似度

0　引 言

随着经济的高速发展，信息技术日新月异，网络使用更加广泛，信息交流渠道变得多样化，社交环境也愈加复杂化。因此，从复杂网络[1]中挖掘隐藏的社团对研究网络的结构属性具有重要意义。现实世界中，如广泛使用的Email网络、万维网、遍及全球的Internet、生物系统中的蛋白质网络、社交网络以及无线mesh网络[2-3]等，都属于复杂网络的范畴。挖掘复杂网络潜在的社团结构，对于舆情控制、预防病毒传播、对未知生物功能的预测[4-6]等重要重大。

节点特征属性的复杂性、网络拓扑结构的复杂性、节点与结构之间的相互影响以及网络之间的相互影响，这都是复杂网络的复杂性所在。复杂网络中的社团结构体现在社团内部的节点连接相对紧密，社团之间的节点连接相对稀疏[7]。

近年来，复杂网络中社团的挖掘得到了不少专家学者的关注。其中，采用层次聚类[8]是一种典型的社团挖掘算法。该算法包括分裂式层次聚类和聚合式层次聚类两种，最具代表性的分裂式层次聚类算法为GN算法[9]。由美国密歇根大学的Girvan等人提出的基于边介数[10]的社团发现算法，则包括最短路径边介数、随机游走边边介数以及电流边边介数。随后，由密歇根大学的Newman等人提出了社团划分质量函数-模块度[11]度量，根据检测模块度函数值大小来选取最佳的社团结构。另外，Newman在已有算法的基础上提出了一种快速社团发现算法——Newman算法[12]。该算法属于聚合式层次聚类算法，算法起初把网络中每一个节点作为一个独立的社团，每次选择两个能使模块度函数值Q增加最大的社团进行合并，直至Q值不再增加为止。

此外，Raghavan等人[13]提出了一种简单快速的标签传播算法（Label Propagation Algorithm，LPA）[14]。该算法具有近乎线性的时间和空间复杂度。Blondel则提出了一种基于贪婪层次聚类的BGLL算法[15]，该算法基于局部模块度最优化思想。还有研究者提出了多种不同的社团结构划分算法[16]，如谱方法[17]、FN算法[18]等。

本文提出一种基于最短路径特征，根据最短路径数目的特征计算每个节点的中介系数而获取社团中心，根据最短路径长度的特征计算节点之间的相似度值，取所有节点的平均相似度值[19]作为划分社团的阈值，以构成类似于聚类[20]的模型，最后将与社团中心的相似度值大于阈值的节点进行归类，按照此过程不断迭代，至节点集为空。最后，采用标准化互信息（Normalized Mutual Information，NMI）[21]和模块度（Modularity）[22]检测社团结构的紧密性。

1　基本概念

为了研究复杂网络的结构属性，定义了最短路径特征、相似度和划分阈值等概念，并提出了中介系数的定义。

1.1最短路径特征

基于最短路径特征的启发，定义了两种不同的概念：一种是最短路径的数目特征；另一种是最短路径的长度特征。其中，最短路径的数目特征应用于计算中介系数，而最短路径的长度特征则应用于获取节点的相似度。

1.2中介系数

定义节点影响力的中介系数：

式中，pjk表示节点j和节点k之间的最短路径数目，pijk表示节点j到节点k之间的pjk条最短路径中经过节点i的最短路径数目，表示网络节点集内每对节点的最短路径中实际经过节点i的最短路径数目，表示所有网络节点对的最短路径中可能经过节点i的最短路径数目最大值。

1.3节点相似度

定义网络节点的相似度：

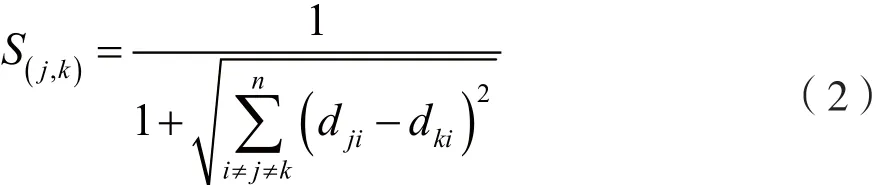
式中，dji、dki为节点j、k到节点i的最短路径长度（连接边数），S(j,k)的取值域为（0,1]。

1.4划分阈值

定义社团结构划分的阈值：

2　算法描述

2.1基本思想

通过网络中某个节点的最短路径数目来刻画节点在网络拓扑结构中的重要性和影响力，计算出网络中每一个节点的中介系数，并由大到小进行排序。通过比较网络中任意两个节点到另外某一个节点的最短路径长度差值，来判断这两个节点的相似度。按照聚类的思想，计算节点对的平均相似度值进行社团结构的划分。

2.2算法主要步骤

（1）由式（1）计算网络中每个节点的中介系数值Bi，并降序排列存储于一维数组B[]中。

（2）根据式（2）获取网络中所有节点对的相似度值S(j,k)，并存入相似度矩阵S中。

（3）按照式（3）求出社团结构的划分阈值λ。

（4）取一维数组B[]中最大元素所对应的节点作为社团中心。

（5）取网络中所有与该社团中心的相似度值大于阈值λ的节点并加入到该社团，最后在网络节点集中删除这些节点。

（6）判断网络节点集是否为空，如果为空，则算法结束；否则重复步骤（4）至步骤（6）。

2.3算法时间复杂度分析

SPCDA算法的主要时间开销包括计算网络中每个节点的中介系数值Bi和计算网络中所有节点对的相似度值S(j,k)。其中，计算网络中n个节点的中介系数值Bi，有n个网络节点，且每一个节点都要匹配成节点对，则需要循环次，所以这部分的时间复杂度是O[n(n-1)(n-2)/2]；然后，计算节点对的相似度，网络中有n个节点，则需要循环次，因此该部分的时间复杂度是由此，SPCDA算法的总时间复杂度为：

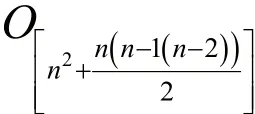
3　实验结果与分析

为了验证本文提出的SPCDA算法的有效性，将其在人工合成网络LFR benchmark和两个经典的真实社会网络上进行实验，并与GN算法、LPA算法进行比较。仿真实验环境：Intel Core i5 2.20 GHz的CPU，8 GB内存，1T硬盘容量，Windows 8操作系统；实验工具为Mysql 5.5和Matlab R2009a。

3.1评价标准

本文采用New-man[12]和Girvan[10]提出的标准化互信息（Normalized Mutual Information）NMI和模块度函数Q作为衡量社团划分结果的标准。

3.1.1标准化互信息NMI

标准化互信息NMI[21]定义如下：

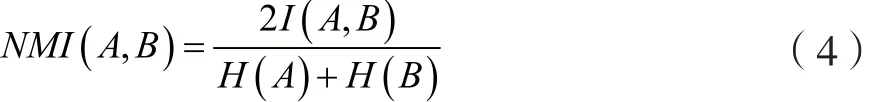
式中，A、B分别表示真实的社团集合和通过算法划分得到的社团结果，I(A,B)是A、B两个向量的交互信息，H(A)和H(B)分别表示A向量和B向量的标准熵。

3.1.2模块度函数

模块度[22]函数定义如下：

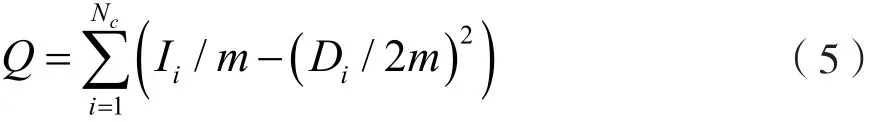
式中，Ii表示第i个社团内部边的数目，Di表示第i个社团中节点的度之和。

3.2LFR人工合成网络

在LFR网络中，设置不同的数据参数值分别测试SPCDA、GN、LPA三种算法。其中，S为社团的规模，Smin为社团的最小规模，Smax为社团的最大规模，Dmax为最大节点度，Dave为平均节点度，N为网络的节点个数，度指数t1=2，社团指数t2=3，γ为混合参数。LFR人工数据集的各种参数取值如表1所示。

表1　LFR数据集参数值

SPCDA、GN、LPA三种算法分别划分LFR人工网络，实验得到的标准化互信息NMI随混合参数γ的变化曲线如图1所示。取四组不同的参数，分别得到图1（a）、图1（b）、图1（c）、图1（d）四个子图。

图1　LFR数据集NMI值对比

其中，图1（a）设置的最小社团规模为10，最大规模为50，平均节点个数为20，最大节点个数为50，此时SPCDA算法划分LFR人工网络的NMI值介于GN和LPA之间；图1（b）设置的最小社团规模为20，最大规模为100，平均节点个数和最大节点个数与图1（a）图相同，在混合参数γ为0.5时，SPCDA算法划分LFR网络的效果开始略有降低，均低于另两种算法；图1（c）设置的社团规模与图1（a）图相同，但平均节点个数为40，最大节点个数为50，此时SPCDA算法划分LFR人工网络的效果接近GN算法，两者的效果均远优于LPA算法；图1（d）设置的社团规模与图1（b）相同，但平均节点个数和最大节点个数与图1（c）图相同，在混合参数γ为0.1到0.3之间时，GN算法和SPCDA算法的划分效果相接近；在混合参数γ处于0.3至0.7之间时，SPCDA算法划分LFR人工网络的效果最佳。分析图1结果表明：SPCDA算法划分社团精度介于LPA与GN之间，但针对算法时间复杂度分析，SPCDA算法时间复杂度更低，这也将在真实社会网络中得以验证。

3.3真实社会网络

在真实社会网络中，选取具有代表性的Zachary俱乐部网络和美国大学足球联盟网络进行实验。

3.3.1Zachary俱乐部网络

Zachary空手道俱乐部网络由34个节点78条边组成。一个节点对应一个成员，一条边对应成员之间的社交关系。由于就是否提高俱乐部收费的问题导致俱乐部主管和校长之间发生矛盾，从而形成了分别以主管和校长为中心的两个不同的社团。根据本文提出的SPCDA算法，由式（1）计算出Zachary网络的中介系数。其中，中介系数最大的节点为节点1，B1=0.835；其次是节点34，B34=0.799。网络中节点的平均相似度值λ=0.428，Zachary空手道俱乐部网络实验划分结果如图2所示。

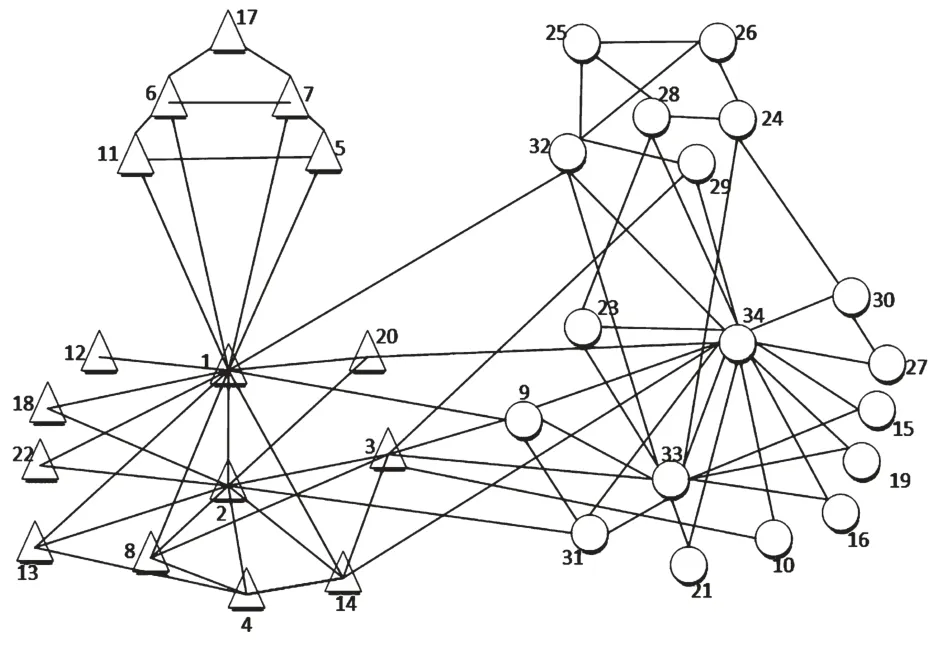
图2　Zachary俱乐部网络划分结果

本文算法与LPA、GN算法在Zachary空手道俱乐部网络进行实验比较。其中，SPCDA算法在划分社团数目为2时到达最大模块度，即社团数目为2时，该社团的结构最清晰。在社团数目为2时，SPCDA算法划分该社团的平均模块度Qave=0.4109，得到最佳社团结构的耗时T=54.3 ms；GN算法划分社团的平均模块度Qave=0.4133，耗时T=150.4 ms；LPA算法划分社团的平均模块度Qave=0.340 7，耗时T=52.7 ms。划分Zachary俱乐部网络的社团结构比较结果如图3所示。

图3　三种算法划分的社团数目对应的模块度变化

其中，SPCDA、GN、LPA三种算法划分Zachary俱乐部网络的模块度函数Q值均在社团数目为2时达到最大，并在之后开始逐渐减小。LPA算法减小的幅度较大，而GN算法与SPCDA算法减小幅度较平缓。在社团数目为5时，GN算法和SPCDA算法的模块度函数Q值几乎相等。在社团数目为7时，GN算法减小的幅度加剧，且低于SPCDA算法的划分精度。通过对比分析划分社团的个数、模块度、运行时间三个方面的实验结果，可见SPCDA算法在时间复杂度和准确性上进行了有效权衡，可以用较少的时间来准确划分社团。

3.3.2美国大学足球联盟网络

美国大学足球联盟网络由115个节点和616条边组成，其中网络中的节点对应球队，边对应两个球队之间的比赛联系。根据SPCDA算法对美国大学足球联盟网络进行社团划分，得到如图4所示的实验结果。

图4　美国大学足球联盟网络社团划分结果

其中，SPCDA算法划分美国大学足球联盟网络实验结果详情如表2所示。

表2　美国大学足球联盟网络社团划分结果详情

本文算法划分美国大学足球联盟网络得到10个社团。此时的社团结构最清晰，划分该社团的平均模块度Qave=0.5962，得到最佳社团结构的耗时T=464.4 ms。GN算法平均模块度Qave=0.6001，耗时T=5812.8 ms；LPA算法划分的平均模块度Qave=0.5879，耗时T=419.7 ms。具体的，与GN、LPA算法在划分社团结构上的实验结果如图5所示。

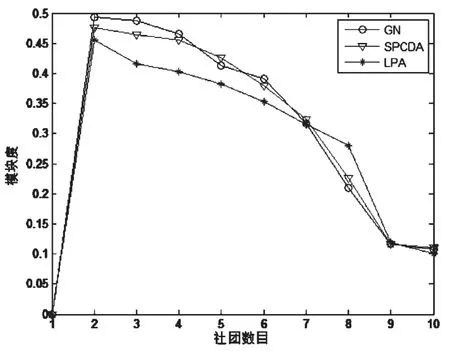
图5　三种算法划分的社团数目对应的模块度变化

其中，在社团数目为10时，SPCDA、GN、LPA三种算法均取得最大模块度函数Q值。此后，GN算法划分美国大学足球联盟网络的模块度函数Q值大幅度降低，而SPCDA算法和LPA算法均直到社团数目为12之后才开始下降，并在社团数目为10至12之间，其模块度函数Q值几乎维持不变。在社团数目增长到12时，LPA算法也开始出现大幅度降低的现象，而SPCDA算法依然保持小幅度下降，直至社团数目为14时，才开始加剧下降幅度。通过实验结果分析，本文算法划分社团的准确度比LPA算法更高，接近GN算法，而运行时间比GN算法更少。由此可知，本文算法在划分社团的精度和时间复杂度这两个衡量指标上的综合，得到了有效提高。

4　结 语

SPCDA算法是基于最短路径特征的启发，每次选取节点集合中中介系数最大的节点作为社团中心。根据最短路径的相关概念计算节点之间的相似度值，取所有节点的平均相似度值作为划分社团的阈值。将与社团中心的相似度值大于阈值的节点进行归类，按照此过程不断迭代，至节点集为空。通过仿真实验结果可知，SPCDA算法能够有效发现社团结构，并且划分社团的准确度较高，算法的时间复杂度较低。

[1] 赖大荣.复杂网络社团结构分析方法研究[D].上海:上海交通大学,2011. LAI Da-rong.Study on the Analysis Method of Complex Network Community Structure[D].Shanghai:Shanghai Jiao Tong University,2011.

[2] Kun Xie,Xin Wang,Jigang Wen,et al. Cooperative Routing with Relay Assignment in Multi-radio MultihopWireless Networks[J]. IEEE/ACM Transactions on Networking (TON), 2016,24(02): 859-872.

[3] Jigang Wen,Jiannong Cao,Kun Xie,et al.User Density Sensitive P2P Streaming in Wireless Mesh Networks[J].Journal of Parallel and Distributed Computing,2011,71(04):573-583.

[4] Spirin V,Mirny L A.Protein Complexes and Functional Modules in Molecular Networks[C].Haetwell Proceedings of the National Academy of Science.New York:The National Academy of Sciences of the USA,2003:12123-12128.

[5] Wilkinson M D,Huberma A B.A Method for Finding Community of Related Genes[A]//Mill R.Proceedings of the National Academy of Sciences[C].Palo Alto:Chemical Abstracts,2007:5241-5248.

[6] Guimera R,Amara A L.Functional Cartography of Complex Metabolic Networks[J].Nature,2005,433(07):895-900.

[7] 刘瑶.社会网络特征分析与社团结构挖掘[D].成都:电子科技大学,2013. LIU Yao.Characteristics of Social Network and Community Structure Mining[D].Chengdu: University of Electronic Science and Technology,2013.

[8] Brodka P,Saganowski S,Kazienko P.Group Evolution Discovery in Social Networks[A].Kazien-ko P.Proceedings of International Conference on Advances in Social Networks Analysis and Mining[C].New York:IEEE Computer Society,2011:247-253.

[9] 胡芳.复杂网络节点中心性多元评估与社团探测新算法研究[D].武汉:华中师范大学,2015. HU Fang.Research on the New Algorithm of Multi Evaluation and Community Detection in Complex Network Nodes[D].Wuhan:Huazhong Normal University,2015.

[10] Girvan M,Newman M E J.Community Structure in Social and Biological Networks[J].Proceeding of the National Academy of Sciences of the United States of America,2002,9(12):7821-7826.

[11] Jin J,Liu Y,Xu k,et al.Novel Dynamic Evolution Model based on Improved Cellular Auto mata in Hierarcal Complex Networks[J].Journal of Communicatio ns,2013,8(12):862-869.

[12] Newman M E J.Fast Algorithm for Detecting Community Structure in Networks[J].Physical review E,2004,69(06):066133.

[13] Raghavan U N,Albert R,Kumara S.Near Linear Time Algorithm to Detect Community Structures in Large Scale Networks[J].Physical Review E,2007,76(03):036106.

[14] 刘攻申,张浩霖,孟魁等.非随机的标签传播社区划分算法[J].上海交通大学学报,2015,49(08):1168-1173. LIU Gong-shen,ZHANG Hao-lin,MENG Kui,et al.A Non Random Label Propagation Algorithm[J].Journal of Shanghai Jiao Tong University,2015,49(08):1168-1173.

[15] Blondel V D,Lambiotee R,lefebvre E,et al.Fast Unfolding of Communities in Large Networks[J].Journal of Statistical Mechanics,2008,2(25):1000-1008.

[16] 骆志刚,蒋晓舟.复杂网络社团发现算法研究新进展[J].国防科技大学学报,2011,33(01):47-52. LUO Zhi-gang,JIANG Xiao-zhou.New Progress in the Study of Complex Network Community Discovery Algorithm [J].Journal of National University of Defense Technology,2011,33(01):47-52.

[17] 周继超,刘建生.确定FCM聚类中心的自动谱聚类社团发现算法[J].江西理工大学学报,2016,1(37):80-86. ZHOU Ji-chao,LIU Jian-sheng.An Algorithm for Automatic Spectral Clustering in the Determination of FCM Clustering Center[J].Journal of Jiangxi University of Science and Technology,2016,1(37):80-86.

[18] Zhang Y P,Wang Y,Zhao S,et al.Community Detection Algorithm base on Cover[J].Journal of Nanjing University(Natural Sciences),2013,49(05):539-545.

[19] 梁宗文,杨帆,李建平.基于节点相似性度量的社团结构划分方法[J].计算机应用研究,2015,35(05):1213-1217. LIANG Zong-wen,YANG Fan,LI Jian-ping.A Method for the Division of Community Structure based on the Similarity Measure of Nodes[J].Computer Application Research,2015,35(05):1213-1217.

[20] 杨博,刘大友,金博等.复杂网络聚类方法[J].软件学报,2009,20(01):54-66. YANG Bo,LIU Da-you,JIN Bo,et al.Complex Network Clustering Method[J].Journal of Software,2009,20 (01):54-66.

[21] Luo Z G,Jiang X Z.New Progression Community Detection in Complex network [J].Journal of National University of Defense Technology,2011,33(01):47-52.

[22] Newan M E J,Girvan M.Finding and Evaluating Community Structure in Networks[J].Physical Review E,2004, 69(02):026113.

杨艳新（1989—），男，硕士研究生，主要研究方向为计算机网络、数值分析；

熊小峰（1965—），男，硕士，教授，主要研究方向为数学建模及应用，数值计算与数值分析；

乐光学（1963—），男，博士，教授，主要研究方向为计算机网络与分布式系统、无线Mesh网络技术。

Community Discovery Algorithm based on Shortest Path Feature

YANG Yan-xin1,2, XIONG Xiao-feng1, YUE Guang-xue1,2
（1.School of Science, Jiangxi University of Science and Technology, Ganzhou Jiangxi 341000，China；2.College of Mathematic Physics and Information Engineering, Jiaxing University, Jiaxing Zhejiang 314000，China）

For quickly and accurately mining community structure the community discovery algorithm SPCDA(Shortest Path feature community discovery algorithm) based on the shortest path feature is proposed. This algorithm, based on the enlightenment of shortest path feature and the number of shortest path, calculates the intermidiary coefficient of each node and captures the community center, and in accordance with the shortest path calculates the similarity of between the nodes, then taking the average similarity of all nodes as the threshold value for dividing social community,constructs a model similar to clustering, and finally the community centers with the similarity value greater than the threshold value of the node are classified, and the algorithm continues this iterative process until the node set becomes empty. The algorithm is applied to the artificially synthetic networks and two classic real social networks. Comparison with GN algorithm and LPA algorithm, indicates that SPCDA algorithm could more accurately and quickly mine the hidden community structure.

community structure; shortest path; intermediary coefficient; similarity

TP301.6

A

1002-0802(2016)-08-01034-07

10.3969/j.issn.1002-0802.2016.08.015

2016-04-20;

2016-07-19

date:2016-04-20;Revised date:2016-07-19