大规模MIMO系统中导频污染空域降低方法*

尚国武，李 辉

（中国科学技术大学 中国科学院无线光电通信重点实验室，安徽 合肥 230026）

大规模MIMO系统中导频污染空域降低方法*

尚国武，李 辉

（中国科学技术大学 中国科学院无线光电通信重点实验室，安徽 合肥 230026）

导频污染是限制大规模MIMO通信系统总体性能的主要瓶颈。针对导频污染问题，提出了一种基于二维来波方向（2D-DOA）估计的空域降低方法。首先对该方法进行理论分析，然后根据提出的两种基于压缩感知（CS）的2D-DOA估计方法获得目标信号的DOA估计值，进而利用该估计值对接收信号做预处理，以达到抑制干扰和噪声，降低导频污染的目的。仿真结果表明：所提CS-2D-DOA估计方法是有效的；所提空域降低方法可以大幅度降低导频污染，显著提升系统性能。

大规模MIMO；导频污染；压缩感知；2D DOA估计

0　引 言

大规模MIMO（Massive MIMO或Very Large MIMO）技术已成为5G无线通信网络中的研究热点之一[1]。大规模MIMO具有提高能量效率、系统容量、频谱效率等诸多优势。理论上讲，当天线数目趋于无穷大时，大规模MIMO可完全消除热噪声和小尺度衰落的影响，因此系统性能主要受限于导频污染[2]。导频污染的存在会降低信道估计的准确性，是限制大规模MIMO系统性能的瓶颈[3]。因此，降低导频污染可以提升通信系统的整体性能，具有重大的工程意义。

目前，降低导频污染是一个开放的课题，国内外专家学者提出了一些减少导频污染的方法[4-8]。但绝大多数方法是基于功率控制、预编码、导频分配等策略实现的。文献[8]提出了一种次优的空域方法，利用目标信号的来波方向抑制导频污染的影响。但是，该文忽略了一个重要事实：在实际的通信系统中，信号的来波方向是由方向角和仰角构成的。虽然文献[8]的工作存在片面，但是为解决导频污染问题提供了新思路。经典的DOA估计算法及其衍生的诸多算法如MUSIC[9]、SPRIT[10]等，需要多快拍的采样数据，进行协方差矩阵以及奇异值分解的运算，还需要大量数据分析信号的统计特性。然而，在大规模MIMO系统中，天线数目很多，接收信号数据规模很大，提高了传统经典的DOA估计算法的运算复杂度，效率很低。

本文从空域的角度出发，提出了一种降低导频污染的方法。为了获得目标信号的仰角与方位角，本文还提出了两种高效的基于压缩感知的单快拍2D-DOA估计算法。本文首先给出了空域降低导频污染方法的理论分析，然后给出了2D-DOA的压缩感知模型的推导以及估计算法，最后将DOA估计值应用到空域方法中，实现综合仿真。仿真结果表明，本文提出的空域方法是可行的、有效的，可以大幅度抑制导频污染，大大提升系统性能。

1　系统模型

系统模型如图1所示。本文考虑的是一个多小区多用户大规模多输入多输出系统。该系统有L个小区，每个小区有K个用户。假设每个小区中，基站配置M×M的方形阵列天线，用户端是单一天线；所有小区的导频使用相同的频带和导频序列；同一个小区内的导频相互正交，且频率复用因子为1。不失一般性，设1号小区内的基站和用户分别是目标基站和目标用户。

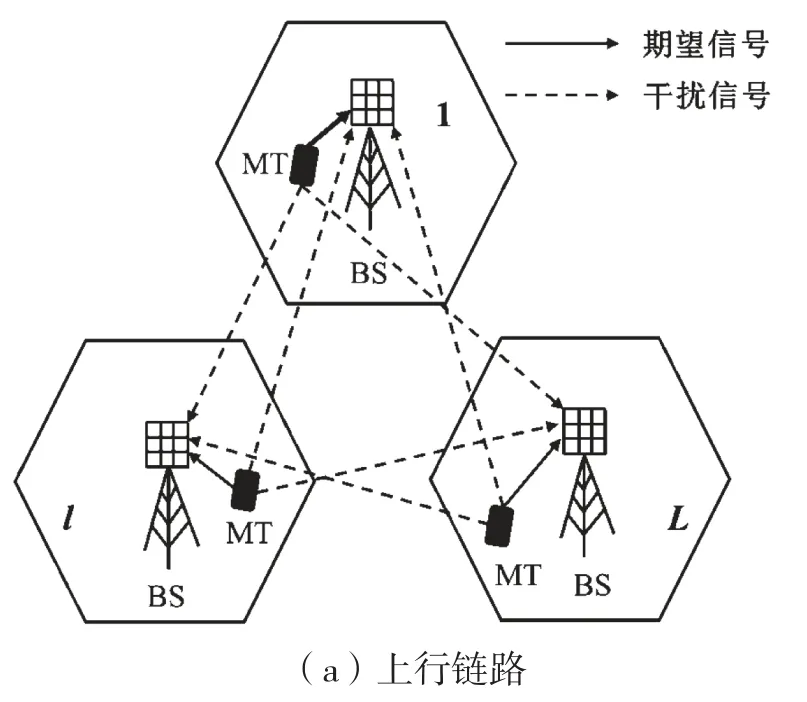
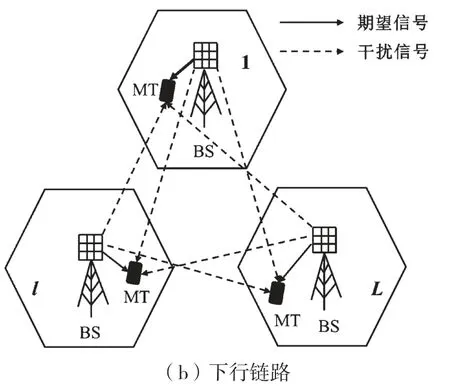
图1　系统模型

由于同一个小区内的导频序列相互正交，因此可简化为每个小区只有一个用户，即K=1。

上行链路中，目标基站接收信号R可以表示为：

式中，PU为用户的信号功率（假设所有用户均相同），Hl表示第l个用户到目标基站的信道矩阵，N为均值为0、方差为σ2的加性高斯白噪声。

如果不 考虑多径效应，采用方形阵列天线的信道矩阵可表示为：

式中，θl与φl分别表示用户l相对于目标基站的仰角与方位角。α(θl,φl)与β(θl,φl)可以看作由仰角与方位角构成的方向矢量，分别为：

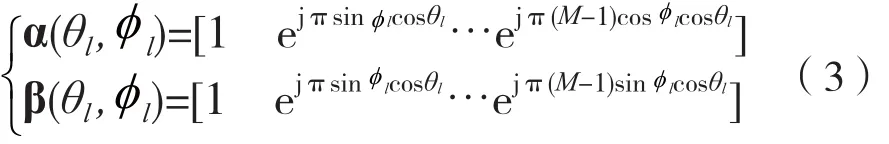
在下行链路中，目标信号的接收信号可表示为：

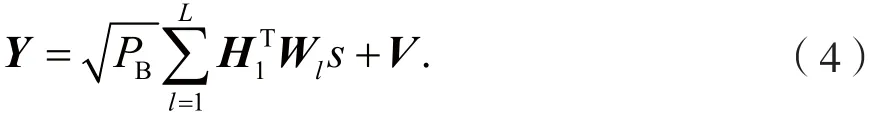
若不采取任何降低导频污染措施，则信道估计结果为：

则目标用户接收信号可以表示为：

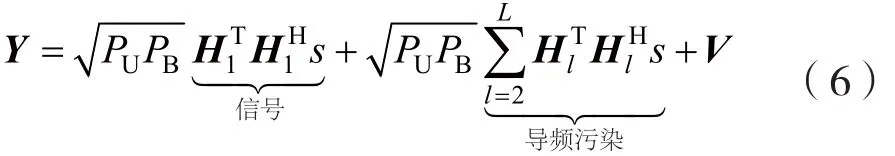
2　导频污染空域降低方法

假设目标用户的2D-DOA是已知的，则可以根据导向矢量的定义式（3）获得α(θl,φl)与β(θl,φl)。根据匹配滤波准则，对接收信号进行预处理，使期望信号在不损失的前提下，抑制干扰信号。

构造如下检测函数：

检测输出为：

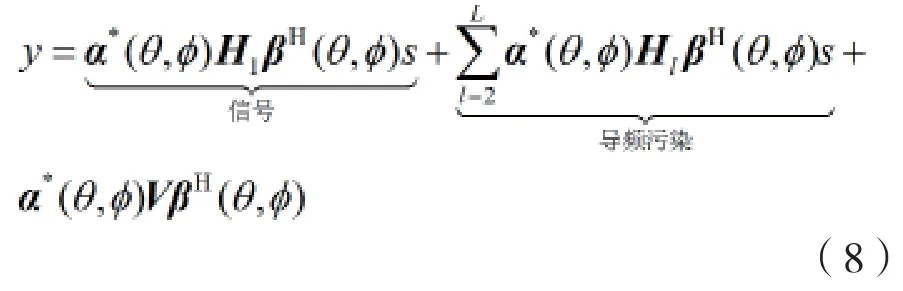
可知，如果目标用户DOA估计足够精确，则期望信号将没有损失；而干扰项将因不匹配而减弱，即导频污染得到了抑制。

由式（6）可知，可将目标信号的信干比（SIR）与信干噪比（SINR）作为衡量导频污染大小的指标。

不采取任何降低导频污染措施情况下，目标信号的SIR与SINR计算公式分别为：

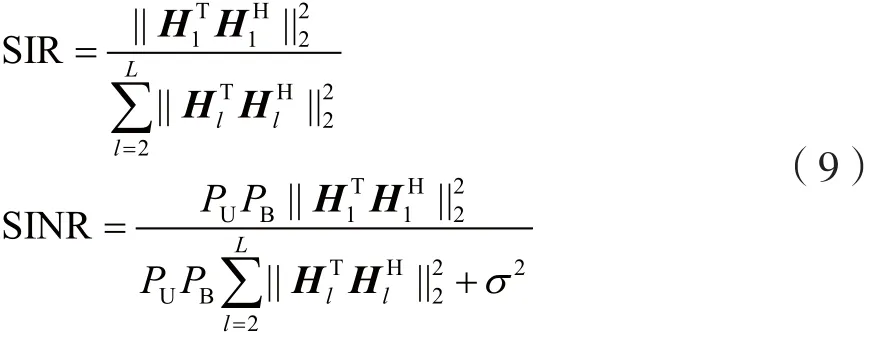
采用本文提出的空域降低导频污染方法后，目标信号的SIR与SINR分比为：

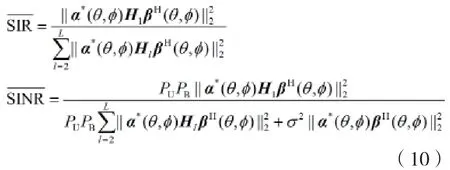
可以证明，采用导频污染降低方法后的目标信号的SIR与SINR均有所提升，表明该空域方法可以降低导频污染。

定义处理前后目标信号的性能增益分别为：

目标信号可以获得的数据速率Ω为：

3　基于压缩感知的2D-DOA估计算法

3.1压缩感知模型

将式（1）中的矩阵按列重排成向量形式，即：

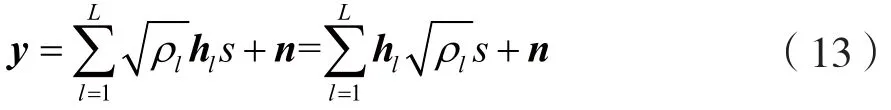
式中，hl可以看作是来波方向为θl,φl的导向矢量。假设将全空间划分为N=N1N2个潜在的来波方向，其中N1, N2分别为对应的仰角和方位角的划分数目，则式（13）可以改写为：

式中，y与n的维度是M×1，A的维度是M2×N，x的维度是N×1，有() L L≪N个非零元素，分别为L个用户的路径损耗ρl(l=1,2,…,L)，x可看作是由L个用户的路径损耗构成的输入向量，即：

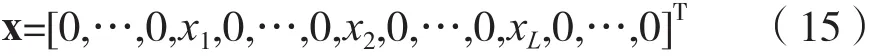
式中，x1,x2,…,xL是ρ1,ρ2,…,ρL的某一组特定排列。

因此，式（14）可以看作是一个压缩感知模型，其中A是观测矩阵，x是稀疏度为L的输入向量，y是接收信号向量。现在已知接收信号向量y和构造的观测矩阵A，只需通过压缩感知求解算法估计出稀疏向量x，再确定非零元素所对应的二维来波方向，即为2D DOA估计值：

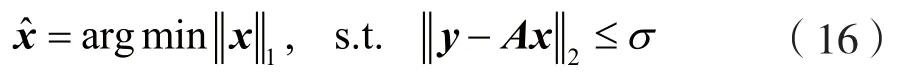
式中，σ是与噪声有关的参数。

导频污染空域降低方法是基于匹配准则实现的，这与匹配追踪（MP）[12]的基本思想类似。MP算法的基本原理是用接收信号与观测矩阵每一列向量求内积找到绝对值最大的元素所对应的位置则为稀疏输入向量的估计结果，然后去除该估计值的影响，迭代执行，直到找到所有目标输入。而这里我们只关注目标信号的来波方向，因此只需要进行一次匹配追踪算法。

优化目标方程为：

式中，集合ζ与ξ分别是θ与φ的划分集合，μ(θ,φ)表示A中来波方向为θ与φ对应的列向量。

3.2观测矩阵的构造

观测矩阵的构造是压缩感知理论中非常重要的一部分，直接关系运算复杂度以及信号恢复的精度。由式（3）可知，方位角与仰角是不可分离的。假设空域方法对估计精度的需求为0.05°，已知仰角与方位角的取值范围分别为（0，90°）与（0，180°），天线规模为M×M，则潜在的2D-DOA有6 480 000个，则观测矩阵的维度为M2×6 480 000。对于大规模MIMO系统，天线数目成百上千，可见直接运算的复杂度非常高。

为了降低运算复杂度，即减少观测矩阵的维度，可以构造合成角,ϑ φ：

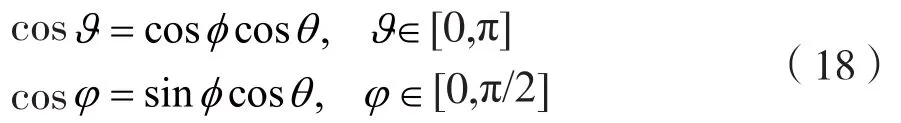
则可以将式（17）转化为对合成角的估计：

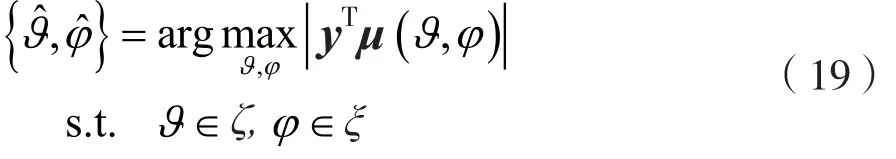
式中，ζ与ξ分别是合成角的划分集合，μ（ϑ, φ）表示A中来波方向为ϑ与φ所对应的列向量。

这样就将原来耦合的角度转化为相互独立的合成角。最后，根据式（20）反解出原来的θ,φ：

显而易见，目标方程式（19）是一个多峰值问题。通过选取合适的划分间隔，可以将其转化为单峰值问题，然后根据角度划分集合构造观测矩阵。

3.32D-DOA估计算法

3.2节介绍了直接采用MP算法极高的运算复杂度，本节将通过对合成角的适当划分改进MP算法，提出两种高效低复杂度的估计算法：二次搜索法（TSM）与迭代搜索法（ISM）。

TSM法分为粗搜索和细搜索两个过程。粗搜索是为了确定2D-DOA的大致范围，其扫描步长为γc，即在角度取值区间以γc进行采样，根据目标方程求出最佳匹配值。此时，最佳匹配值±γc的区间将是单峰值的，将该区间作为细搜索的扫描区间。细搜索则是为了获取足够精确的估计值，扫描步长为γf。该过程与粗搜索类似，在扫描区间内以γf进行采样作为目标方程的取值集合，进而求解出比较精确的估计值。

算法1：TSM

初始化：

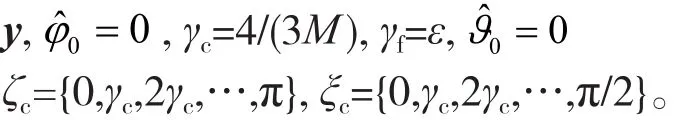
输入：

4：将合成角估计值ϑˆf,φˆf代入（20），求解θˆ, φˆ。

需注意的是，U(x,d;r)表示从x-d到x+d以间隔为y进行采样构成的离散点集合。

ISM法则是对TSM的改进，可以看作是多次搜索法。每一次迭代过程中的扫描区间和搜索间隔都会越来越小，直到满足估计精度需求。ISM方法可以进一步降低计算复杂度，提高运行效率。同样，选择合适的初始扫描间隔，确保在第一次迭代后，将原来的多峰值问题转化为单峰值问题，进而可以采用类似于二分搜索法进行迭代搜索。

算法2：ISM

初始化：

迭代：

4：else k=k+1，返回迭代。

3.4DOA估计算法复杂度分析

以复数乘法运算次数为例，不同DOA估计算法的运算复杂度对比如表1所示。由表1可知，随着天线规模的增加，运算复杂度越来越大。与MP算法对比，TSM与ISM算法的运算次数比MP低很多，约2～3个数量级，ISM的复杂度更低。

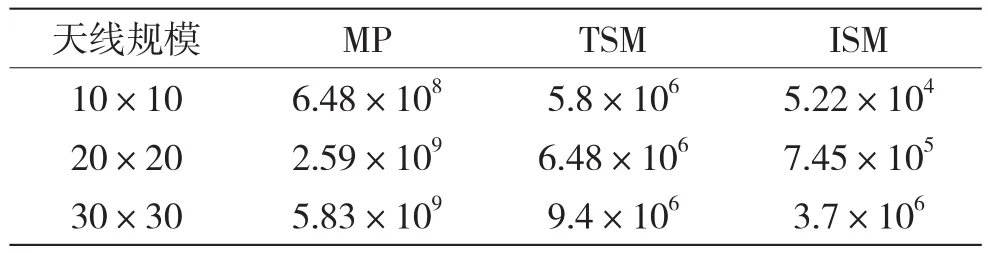
表1　DOA估计算法复杂度对比

4　仿真分析

假设用户空间分布服从均匀分布。在仿真过程中，为了满足可比性，干扰用户的位置随机产生一组，之后不再变化。仿真分别针对无噪声和带噪声两种情形进行。一些基本仿真参数如表2所示。

图2给出了不考虑噪声时，利用本文提出的2D-DOA估计算法实现的目标信号的性能增益与天线规模之间的关系。图中虚线是理论下界。由图2可知，一方面，随着天线规模的增加，信号增益越来越大，表明本文提出的空域降低方法可以有效抑制导频污染，且增加天线数目有助于提升性能。另一方面，两种DOA估计算法的仿真曲线几乎完全重合，其下界与理论下界非常接近，表明本文提出的基于压缩感知的DOA估计算法的估计精度可以满足空域方法的需求。

表2　基本仿真参数

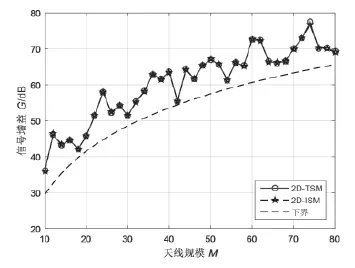
图2　信号增益与天线规模的关系

图3给出了带噪声情况下，不同天线规模时，噪声对导频污染空域降低方法的影响。

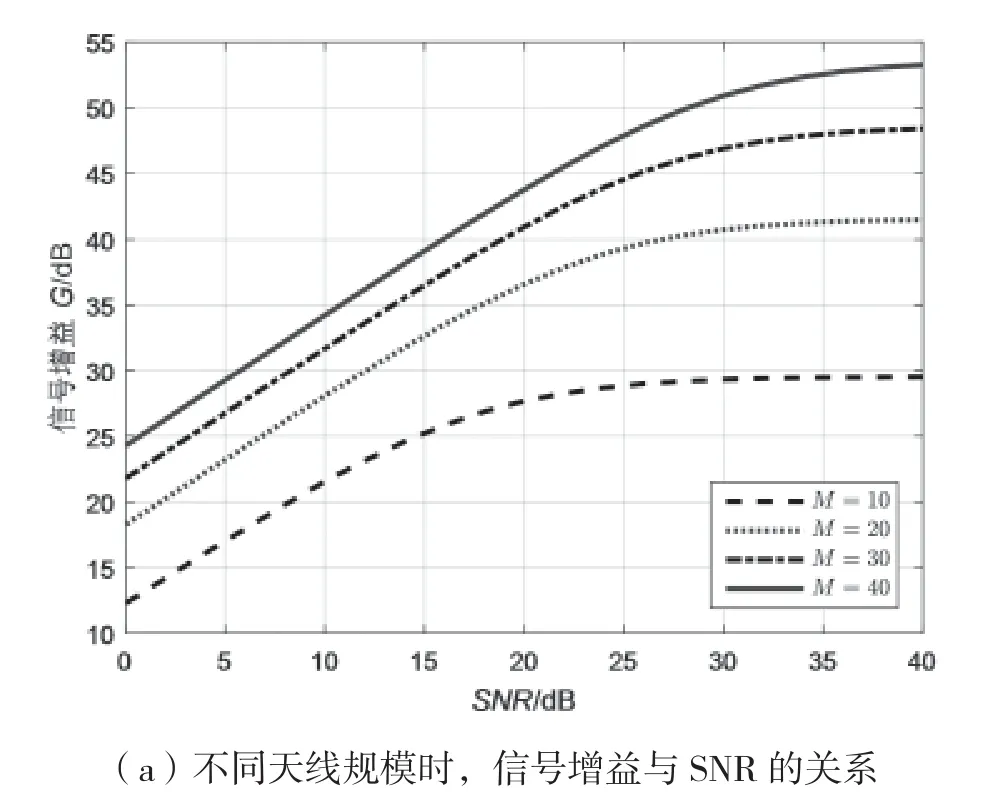
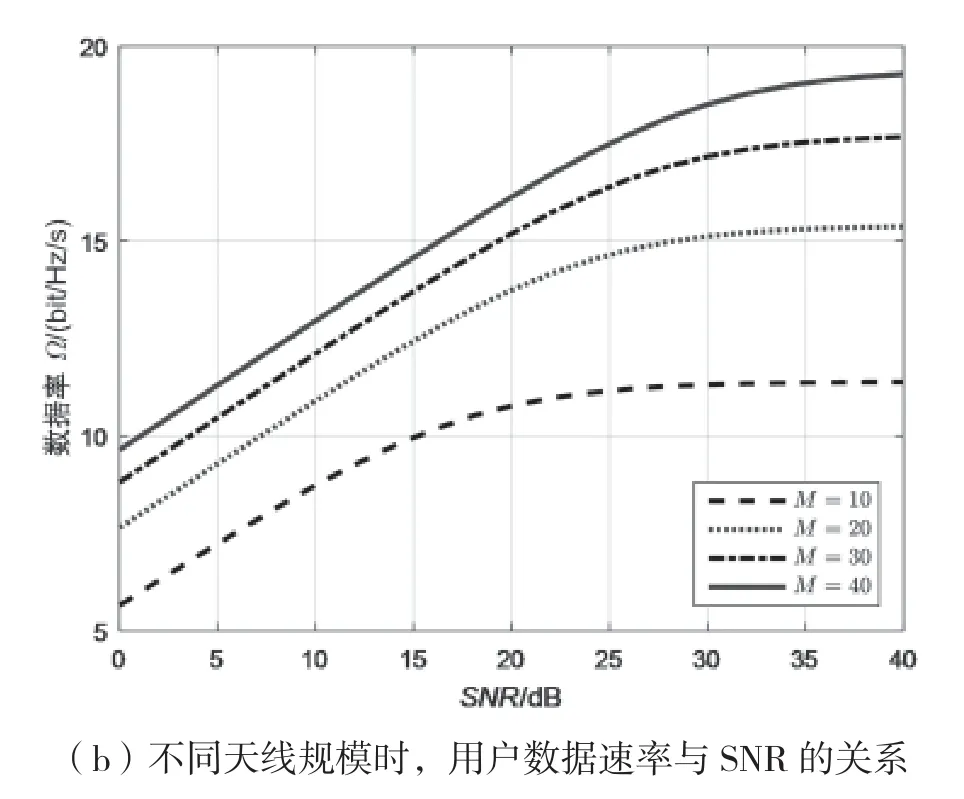
图3　噪声对性能的影响

图3（a）与图3（b）是天线规模分别为10×10、20×20、30×30、40×40时，目标信号处理前后的信号增益与处理后目标用户数据速率与SNR之间的关系（1 000次蒙特卡洛仿真）。由图3可知，当天线数目相同时，随着SNR的增加，目标信号增益先线性增加或趋于平稳。这是因为SNR比较大时，噪声的影响远远大于导频污染的影响，而当噪声减弱时，导频污染的影响占主导。当SNR相同时，目标信号的信号增益（和数据速率）随天线规模的增加而增大，与图2的仿真结果一致。

5　结 语

本文从空域的角度思考，提出了一种基于空域的降低导频污染的方法，利用目标用户DOA信息，抑制导频污染。为了高效准确地获得目标信号的2D-DOA，本文提出了两种基于压缩感知理论的估计算法。仿真结果表明，本文提出的DOA估计算法运算复杂度很低，空域降低导频污染的方法可以有效降低导频污染，大大弥补了大规模MIMO系统的不足，改善了性能。在大规模MIMO系统中，天线数目成百上千，存在大量冗余，能否通过对天线数据的压缩采样进一步降低观测矩阵的维度，降低运算复杂度仍需要进一步进行研究。

[1] 姬晓娜,张卫党,高向川.基于子空间相关信道模型的大规模MIMO信道估计[J].通信技术,2015,48(10):1106-1110. JI Xiao-na,ZHANG Wei-dang,GAO Xiang-chuan. Channel Estimation in Large-Scale MIMO based onSubspace Correlated Channel Model[J].Communications Technology,2015,48(10):1106-1110.

[2] Marzetta T L.How Much Training is Required for Multiuser MIMO?[C].Signals,Systems and Computers,2006:359－363.

[3] WEN Chao-kai,JIN Shi,Kaikit Wong,et al.Channel Estimation for Massive MIMO Using Gaussianmixture Bayesian Learning[J].Wireless Communicatio ns,2015,14(03):1356-1368.

[4] Saxena V,Fodor G,Karipidis E.Mitigating Pilot Contamination by Pilot Reuse and Power Control Schemes for Massive MIMO Systems[C].Vehicular Technology Conference(VTC Spring),2015:1-6.

[5] Liu B,Cheng Y,Yuan X.Pilot Contamination Elimination Precoding in Multi-cell Massive MIMO Systems[C]. Personal,Indoor,and Mobile Radio Communications(PIM RC),2015:320-325.

[6] Ferrante G C,Geraci G,Quek T Q S,et al.Groupblind Detection With Very Large Antenna Arrays in the Presence of Pilot Contamination[J].Mathemati cs,2015,14(12):6579-6594.

[7] Liu F,Meng Q,Zou Y,et al.An Approach to Reduce Pilot Contamination in Large-scale MIMO Systems[C].2015 IEEE 16th International Conference on Communication Technology(ICCT),2015:813-816.

[8] WANG Hua-lei,PAN Zhen-gang,NI Ji-qing,et al.A Spatial Domain Based Method Against Pilot Contamination for Multi-cell Massive MIMO Systems[C].Communications and Networking in China (CHINACOM),2013:218-222.

[9] Petrenko P,Ryabov N,Lyashev V.MUSIC for Spatial Filtering V-MIMO Users in Wireless Communication[C]. Digital Information,Networking, and Wireless Communic ations(DINWC),2015:72-76.

[10] Roy R,Kailath T.ESPRIT-estimation of Signal Parameters Via Rotational Invariance Techniques[J].Acoustics,Speech and Signal Processing,1989,37(07):984-995.

[11] 林波,张增辉,朱炬波.基于压缩感知的DOA估计稀疏化模型与性能分析[J].电子与信息学报,2014,36(03):589-594. LIN Bo,ZHANG Zeng-hui,ZHU Ju-bo.Sparsity Model and Performance Analysis of DOA Estimation With Compressive Sensing[J].Journal of Electronics & Information Technology,2014,36(03):589-594.

[12] 文首先.压缩感知匹配追踪算法的研究[D].合肥:安徽大学,2013. WEN Shou-xian.Matching Pursuit Algorithm for Reconstruction based on Compressive Sensing[D]. Hefei:Anhui University,2013.

尚国武（1988—），男，硕士研究生，主要研究方向为无线通信；

李 辉（1975—），男，博士，副教授，主要研究方向为通信信号处理、无线网络和信息论。

Spatial Domain Method for Pilot Contamination Reduction in Massive MIMO Systems

SHANG Guo-wu, LI Hui
(Key Laboratory of Wireless-Optical Communications, Chinese Academy of Sciences, University of Science and Technology of China, Hefei Anhui 230026, China)

Pilot contamination effect constitutes a major bottleneck for overall performance of massive multiple-input and multiple-output (MIMO) communication systems. Firstly, the theoretical analysis of the method is given. Then the desire signal's DOA is achieved by two 2D-DOA estimation methods based on compressive sensing (CS), which are proposed in this paper. Then the

signal is preprocessed by the estimations, so as to achieve the purpose of suppressing the interference and noise, and reducing the pilot contamination. Simulation results show that the proposed single snapshot CS-2D-DOA estimation methods are effective, while the spatial domain method can reduce pilot contamination greatly, and improve the system performance significantly.

massive MIMO; pilot contamination; compressive sensing; 2D DOA estimation

National High Technology Research and Development Program of China (No.2014AA01A703)；National Natural Science Foundation of China (No.61471335)

TN929.5

A

1002-0802(2016)-08-01011-06

10.3969/j.issn.1002-0802.2016.08.011

2016-04-26;

2016-07-23

date:2016-04-26;Revised date:2016-07-23

国家高技术研究发展计划（863计划）（No.2014AA01A703）；国家自然科学基金（No.61471335）