城市轨道交通末班车时刻表协调优化研究
张安英,胡智敏,张冰清
(1.广东省交通运输规划研究中心,广东广州 510101;2.中铁第四勘察设计院集团有限公司,湖北武汉 430063)
城市轨道交通末班车时刻表协调优化研究
张安英1,胡智敏2,张冰清1
(1.广东省交通运输规划研究中心,广东广州 510101;2.中铁第四勘察设计院集团有限公司,湖北武汉 430063)
在网络运营条件下,以城市轨道交通网络线路间的末班车换乘衔接为研究内容,以换乘衔接客流量最大为目标,同时考虑特定换乘方向约束,建立了网络末班车时刻表优化模型,并针对该模型设计了遗传算法进行求解。结果表明,原始列车时刻表只能衔接19个换乘方向实现610人换乘,设定特定换乘方向时可衔接20个换乘方向并实现858人换乘,优化率达40.66%,文中设计的末班车时刻表衔接和优化模型及遗传算法对换乘站末班车的衔接优化有效。
城市交通;轨道交通;末班车;时刻表;停站时间;遗传算法
在城市轨道交通网络化运营条件下,随着换乘站点的增加,原本独立运营的各条线路通过换乘站产生直接或间接的联系,同时轨道交通客流也通过换乘站实现不同线路的衔接。由于各条线路主要依据本条线路的客流情况确定一天的运营时间,线路结束运营的时刻不尽相同,使轨道交通网络上各车站之间的可达关系呈现动态变化的特点。一条线路的末班车时刻不仅会影响本线路乘客的出行,更大程度上会通过换乘站将影响扩大到整个轨道交通网络。因此,根据换乘客流特点及末班车乘客行为特征对网络末班车发车时刻进行协调,实现各线路末班车在换乘站的整体合理衔接显得尤为重要,这也是对网络化运营的重要补充。
在末班车时刻表优化方面,国内外学者进行了一定研究:Avishal Ceder等建立了在公交网络换乘站中各条线路车辆到达同步化模型;Chung EH.等提出了列车衔接关系维持策略,主要通过改变列车单元对乘客等待时间的影响来界定是否维持该单元衔接关系;Shafahi Y.等建立了以换乘站换乘等待时间最小为目标的城市轨道交通网络时刻表混合整数规划模型,并研究了列车停站时间对换乘衔接的影响;Chowdhury M.S.以减小列车晚点、发车延误等总费用为目标,设计了一套列车实时调度方法;Guihaire V.等从提高时刻表整体质量的角度出发,提出通过调整时刻表的方法来使换乘数量和质量达到最好;Alessandro Chierici等提出了多线地铁列车运行时刻优化方法,考虑了乘客等待时问、旅行时间、舒适度等多种因素;房霄虹初步建立了城市轨道交通网络化运输组织协调理论研究的基本体系,对不同线路模式下列车开行密度的配置方法及结合列车到发时刻在换乘节点内部的衔接与网络换乘节点间的外部协调优化策略进行了探讨;张铭等从换乘时间优化入手建立双层系统,以换乘站作为子系统建立衔接层换乘时间优化模型,然后在协调层调整衔接方案,进而推至全局,达到全局最优,并设计了并行协调算法;罗钦等分析了首末班车的可达性,将列车的到发时间定为刚性影响,乘客走行时间定为柔性影响,构建了首末班车各自的可达性衔接模型;徐瑞华等建立了以换乘乘客候车时间最小为目标的首末班车衔接模型,利用分层协调算法推算了首末班车发车时间域。该文模拟网络运营条件下,以城市轨道交通网络线路间的末班车换乘衔接为研究内容,以换乘衔接客流量最大为目标,同时考虑特定换乘方向的约束,建立网络末班车时刻表衔接模型。
1 换乘站线路衔接过程分析
1.1换乘站换乘客流与列车流到发时序关系
对于换乘站k,在线路l和p的发车间隔确定的前提下,以两线四向互换乘为例,如图1所示,线路l各列车到达换乘站k的时间依次为,各列车的到达时间间隔为为乘客在换乘站k由线路l换乘至线路p的换乘走行时间,twk,l,p为乘客在换乘站k由线路l换乘至线路p的换乘等待时间,实线表示线路l,虚线表示线路p。
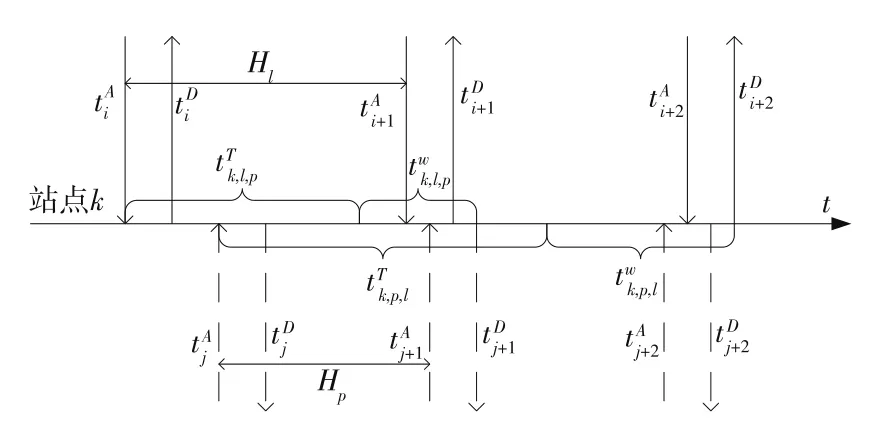
图1 换乘站两线列车到发时间关系示意图
若线路l的第i列车的乘客换乘线路p的第j +1列车,则换乘时间为:

式中:tⅠl,p为由线路l换乘线路p的换乘时间。
又因为线路换乘时间为换乘走行时间与换乘等待时间之和,即

在一个具体的换乘站中,线路间的换乘走行时间依据不同时段(高峰与平峰)以2个值取代,即换乘走行时间是确定的值,则换乘等待时间为:
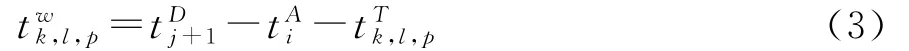
twk,l,p=0,表示换乘乘客到达目标站台不需要等待列车到达,直接上车,是理想中的换乘0,表示换乘乘客需要在目标站台等待列车到达。
1.2换乘站末班车换乘衔接过程分析
由换乘站内换乘流与列车流到发时序关系分析可知:末班车的换乘等待时间应为换出线路的末班车的客流到达换入线路的站台的时间与换入线路的列车到达该站台的时间差。然而换入线路的列车不一定是该线路的末班车,故引入末班车换乘冗余时间。换乘冗余时间指换出线路的末班车的客流到达换入线路的站台的时间与换入线路末班车到达该站台的时间差。下面分为3种情况分析末班车换乘等待时间与换乘冗余时间的异同,以在换乘站k线路l的末班车换乘线路p为例。如图2所示,线路l与p对应的末班车分别为i、j。
(1)当线路l的末班车i的客流换乘的是线路p的末班车j时,换乘等待时间与换乘冗余时间相等,即:

式中:trk,l,p为在换乘站k由线路l末班车换乘线路p末班车的换乘冗余时间。
(2)当线路l的末班车i换乘线路p的末班车j之前列车时,换乘等待时间小于换乘冗余时间,即:

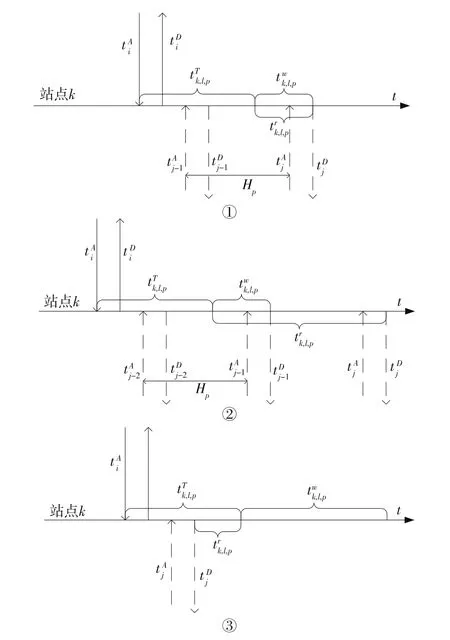
图2 两线路末班车间换乘关系示意图
(3)当线路l的末班车i换乘线路p衔接失败时,换乘等待时间将为无穷大,换乘冗余时间为负值,即:

换乘冗余时间可用于评价末班车衔接关系的可靠性:当换乘冗余时间大于等于零时,换出线路末班车与换入线路末班车的到站时间差值变化不能大于换乘冗余时间,否则将导致该方向换乘失败;当换乘冗余时间为负值时,该换乘方向已经失败。
2 网络末班车时刻表衔接模型的建立
由于线路具有上下行方向,为方便起见,将各条线上下行方向分为2条线路,建立线路集合L、换乘站集合S、各个换乘站各换乘方向的需求集合Q。
2.1换乘站内线路间换乘过程分析
线路i的换乘站集合为Si,线路j的换乘站集合为Sj,如果换乘站k为线路i和j的共同换乘站,由换乘站内部衔接过程分析可知:若线路i的末班车在换乘站k换乘线路j,则需在线路j的末班车离开站点k之前线路i的末班车乘客到达线路j的站台,即有:
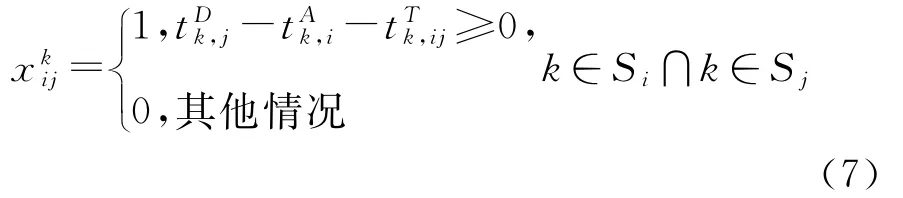
将式(7)化为不等式约束:
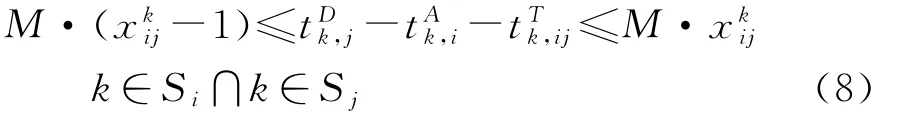
式中:M为足够大的正数。
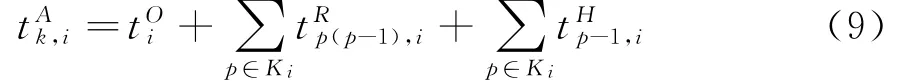
线路i的末班车在站点k的到站时刻为该车发车时刻与在到达站点k之前的各站间行驶时间与各站停站时间之和,数学表达式为:式中:tOi为线路i的末班车发车时刻;为线路i的列车在站点p-1到站点p的行驶时间;p为换乘站k在i线路所经过换乘站Si的序号;tHp,i为在线路i第p个换乘站点k的停站时间。
同理:
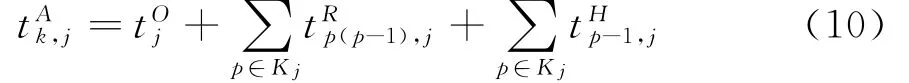
2.2同一换乘站线路间衔接约束
换乘站k为线路i和j的共同换乘站,由换乘站内部衔接过程分析可知:在换乘站k,线路i的末班车换乘线路j成功时,则线路j的末班车换乘线路i失败。在城市轨道交通网络中,在同一换乘站内线路i和j之间的换乘最多只有一个方向换乘成功,数学表达式为:
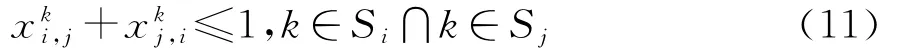
2.3特定换乘方向衔接约束
若特定换乘方向为在换乘站k,线路Ⅰ换乘线路J,则该方向衔接约束为:

对于给定的末班车发车区间:
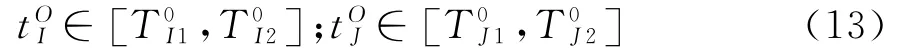
由线路Ⅰ和J各自的到达换乘k的行驶时间和停站时间,可得线路Ⅰ和J的末班车在换乘站k的到站时间区间:
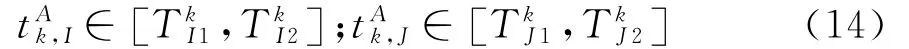
若线路J的末班车在换乘站k最晚离站前,线路Ⅰ的末班车在最早到站时,都不能衔接成功,则该特定换乘方向衔接不能实现,即:
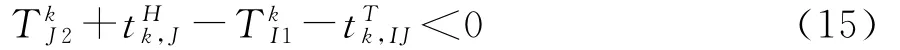
故对于特定换乘方向衔接约束,需根据实际的末班车发车区间判断是否可以衔接成功。
若该换乘方向能衔接成功,则有:

2.4模型构建
在考虑特定换乘方向衔接约束后,根据给定的各线路末班车发车时间域TO和各个换乘站各换乘衔接方向的需求集合Q,为使衔接成功的客流量最大,建立如下目标函数:
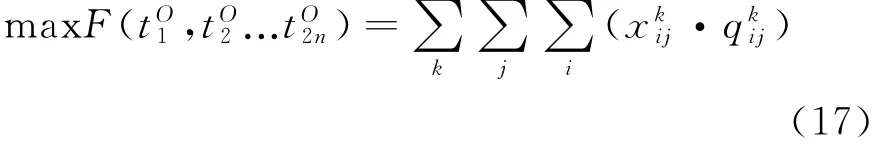
式中:qkij为在换乘站k,线路i末班车换乘线路j的需求量。
式(17)即为网络末班车时刻表优化模型,其约束条件为:
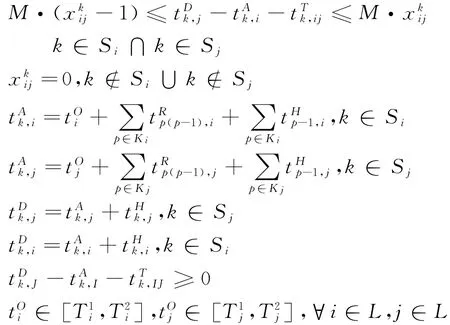
3 算法设计
3.1解空间分析
遗传算法具有快速寻找全局最优解(或准最优解)的能力、能处理复杂非线性系统优化问题、执行简单灵活等特点,被广泛应用于优化问题求解。遗传算法的主要步骤包括设计染色体编码方法、生成初始种群、适应度函数设计、评价种群中各个体的适应度值、通过遗传操作(选择、交叉和变异)产生新的种群直至满足停止迭代条件。
网络末班车时刻表优化模型的决策变量为各线路的发车时间,根据发车时间范围进行二进制编码来构建染色体。染色体由各线路发车时间的二进制顺序排列组成,染色体长度为发车时间对应二进制长度之和。因为特定换乘方向衔接约束的存在使遗传算法每产生一个个体都需要判断是否符合约束条件,同时进行每一次进化和变异的解也需要判断,这会大大降低遗传算法的效率,同时可能造成遗传算法的过早收敛,也可能造成种群的快速死亡,所以需对衔接约束作进一步处理。
利用启发式算法即遗传算法搜索最优解,将特定换乘方向衔接约束转化为对发车时间域的约束,在换乘站k的衔接约束下,线路Ⅰ、J的末班车在站点k的到达时间域分别为:
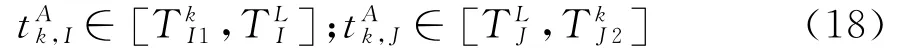
式中:TLⅠ为衔接约束下线路Ⅰ的临界到站时刻。
以满足约束的在站点k到达时间域反推线路Ⅰ和J的末班车发车时间域,在改变后的发车时间域用遗传算法搜索最优解,该最优解可能会在可行域内,也可能在非可行域内。若遗传算法搜索出的最终解在非可行域内,则用搜索域逼近法处理。操作过程如下:利用2个矩形将可行域分割成两部分,将线路Ⅰ和J的在站点k的末班车到达时间域切割为2个搜索域,分别为搜索域1:
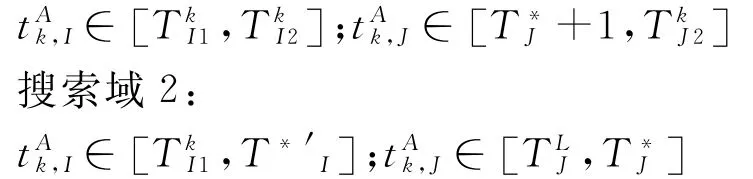
采用遗传算法在2个新的末班车发车时间域继续搜索,得到2个解,若2个解均为可行解,则取较大值作为最优解;若其中一个解为可行解,另一个为非可行解,且可行解不小于非可行解,则取可行域内的解作为最优解;其他情况均要进行下一步分割迭代(如图3所示)。
3.2算法步骤
由网络末班车时刻表衔接模型可知:当没有特定换乘方向约束时,可直接利用遗传算法求解;当考虑特定换乘方向约束时,需先对发车时间域进行约束,然后依据新的发车时间域制订搜索域方案。操作步骤如下:
(1)是否存在特定换乘方向约束,若无,直接进入第2步;若存在,则利用式(12)、式(18)计算满足约束的新发车时间域,然后将新的末班车发车时间域取代原始发车时间域,进入第2步。
(2)在发车时间域内初始化种群。
(3)将各个个体对应二进制染色体转化为具体的实数,依据各条线路到达各换乘站行程时间与各换乘方向走行时间判断各换乘方向的衔接情况,代入适应度函数计算各个体的适应度。
(4)选出适应度最大的个体直接进入下一代种群,不参与种群更新操作。其余个体按照适应度大小,利用轮盘赌算子选择N个染色体(个体)进行交叉操作,取交叉概率P1=0.9对染色体进行两点交叉,将得到的N个新个体选入新种群,没有被选中的交叉个体直接进入下一代种群;变异算子利用基本位变异,取变异概率P2=0.03对染色体进行变异,变异后新个体进入下一代,没有变异的直接进入下一代种群。
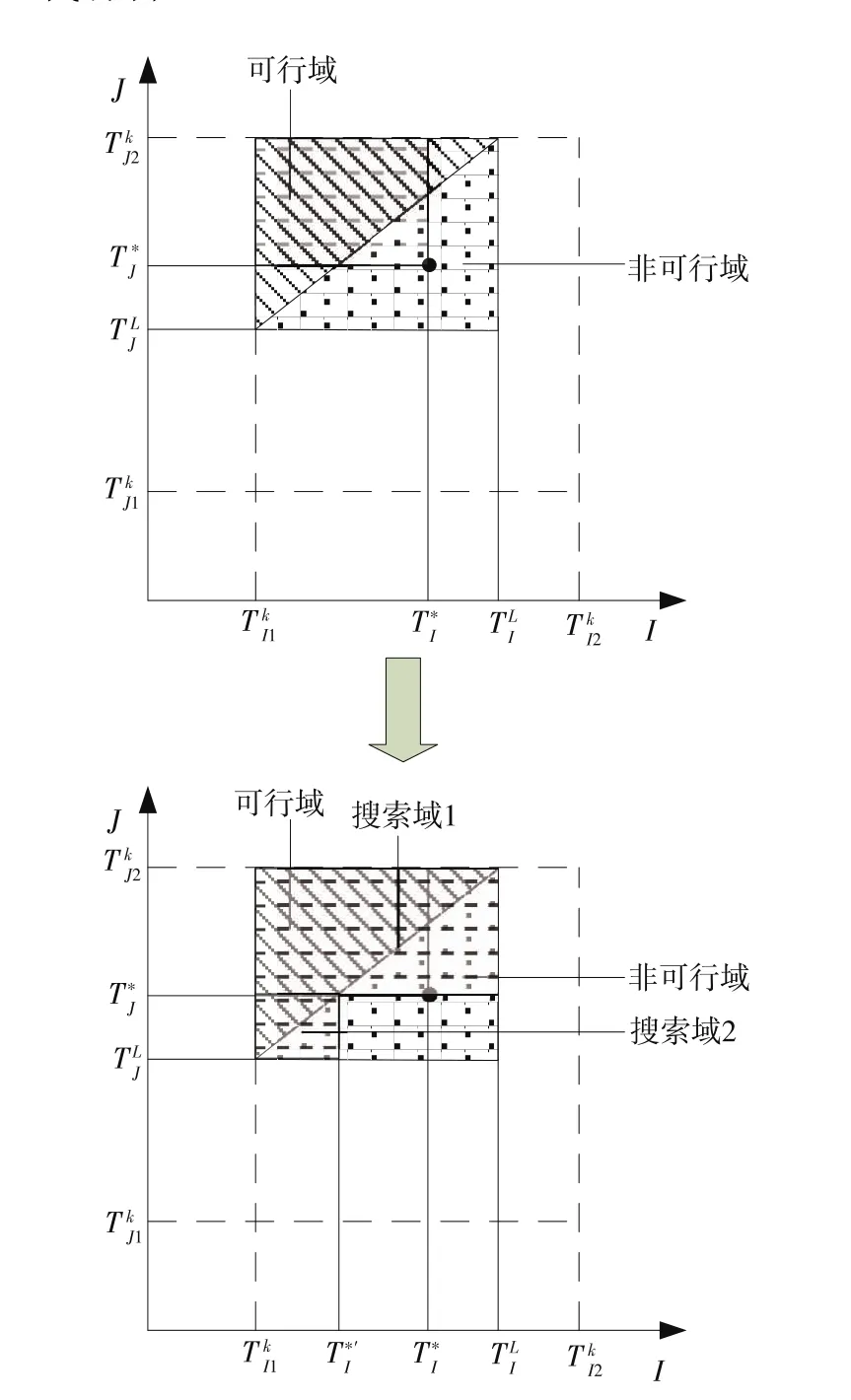
图3 搜索域与可行域关系示意图
(5)判断是否达到最终进化代数,若达到,则输出结果;否则,返回第3步。若是对于特定衔接约束,则进入第6步。
(6)判断输出结果是否在可行域内,若在,则跳至第8步;若不在,则分成若干个搜索域,将各个搜索域分别代入第2步。
(7)将各个搜索域对应的输出结果进行比较,取最大值,进入第8步。
(8)输出结果即为最优解。
4 案例分析
下面以北京市地铁1号线、2号线、5号线构成的网络作为算例进行分析。
4.1算例数据及相关参数
1号线、2号线、5号线构成的网络有5个换乘站。为了区分线路上下行,分别对线路及换乘站编号(如图4所示)。
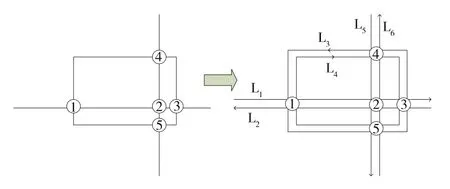
图4 城市轨道交通网络布局示意图
各条线路的末班车原始发车时刻及发车时间域如表1所示。各条线到达各换乘站的运行时间及各站停站时间如表2所示。各换乘站各换乘方向的换乘走行时间如表3所示,换乘需求如图5所示。
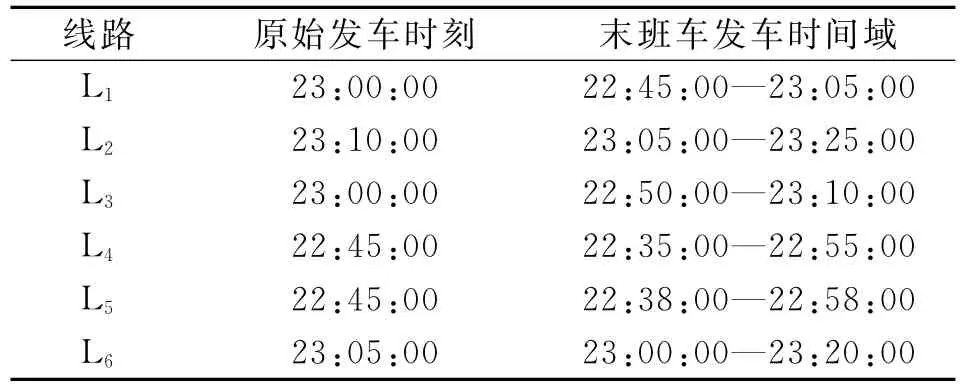
表1 网络中末班车原始发车时刻与发车时间域
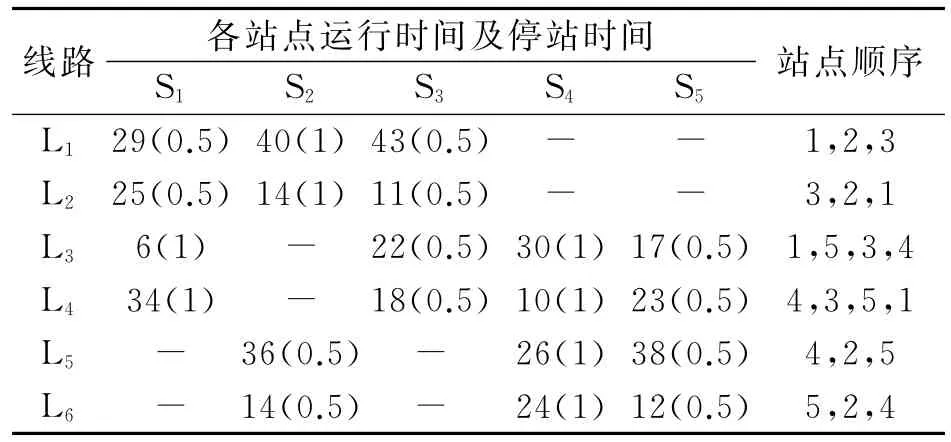
表2 末班车由起始站到各换乘站的运行时间及停站时间min
4.2算法实现及结果分析
若在换乘站S3,L3末班车换乘L1的换乘方向是由市区向市郊方向,为必须实现方向。将该换乘方向约束转化为对L1与L3的末班车发车时间域的约束。当L3的末班车发车时刻取22:55:30时,刚好对L1末班车发车时间域都能实现该方向的衔接;当L3的末班车发车时刻取23:10:00时,只能衔接L1的发车时间域为[22:59:30,23:05:00]。由无换乘方向约束求得的最优解可知其在非可行域内,现利用搜索域逼近可行域方法分成2个搜索域,搜索域1:
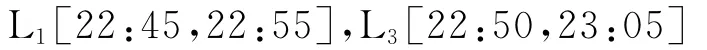
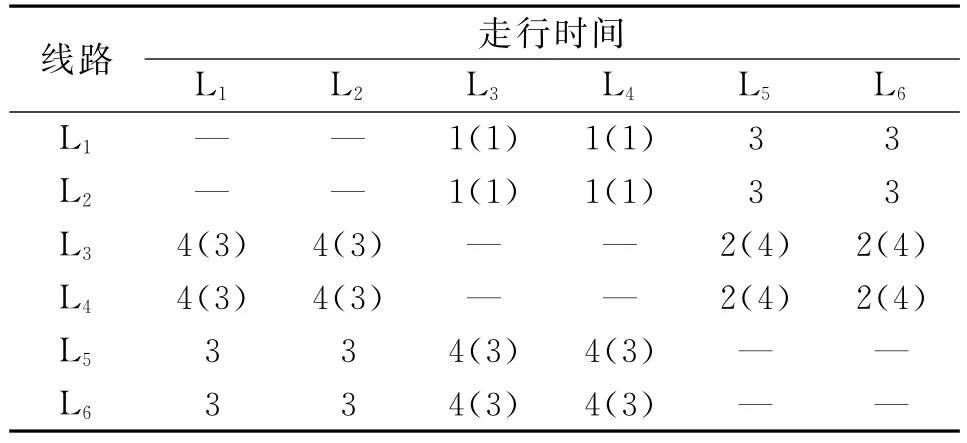
表3 各个换乘方向的换乘走行时间min
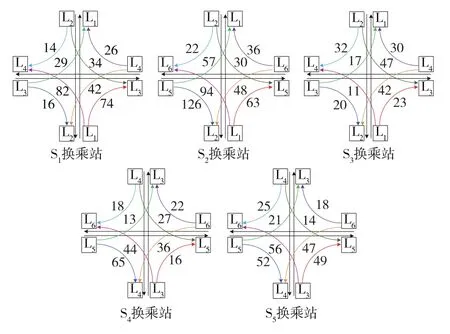
图5 各个换乘方向的换乘需求量(单位:人)
搜索域2:
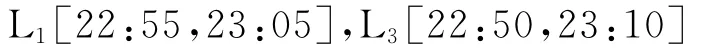
分别用遗传算法对搜索域1和2求解,得到搜索域1:衔接成功的客流量为858人;搜索域2:衔接成功的客流量为816人。对应末班车发车时刻如表4所示,遗传算法适应度变化如图6所示。
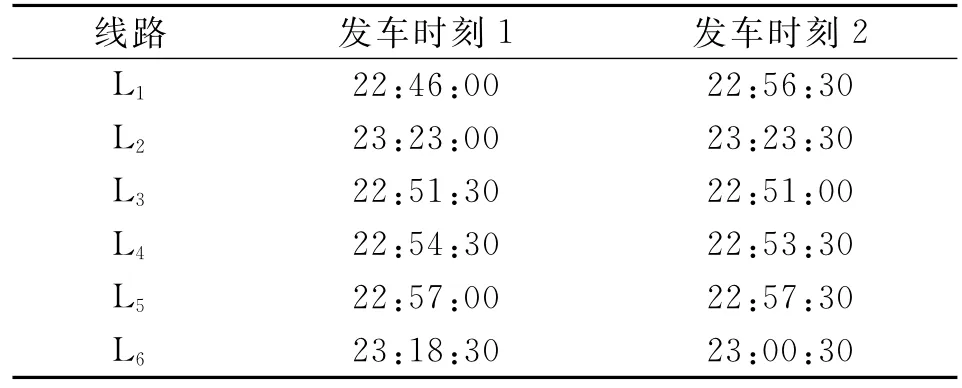
表4 单个换乘方向约束下末班车最优发车时刻
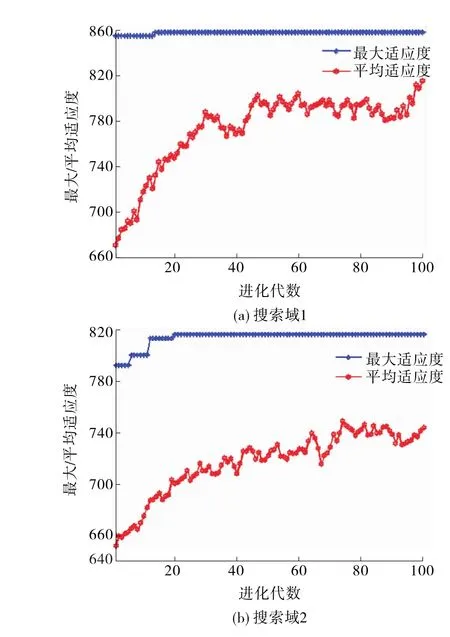
图6 单个换乘方向约束下适应度变化图
比较2个搜索域对应最优解,可知搜索域1中的解优于搜索域2,因此将搜索域1中的解作为满足该方向约束的最优解。各衔接成功方向的具体情况如表5所示。由输出的末班车时刻得到各衔接成功的方向,添加换乘方向约束优化后结果为:衔接20个换乘方向,换乘成功的客流量为858人。
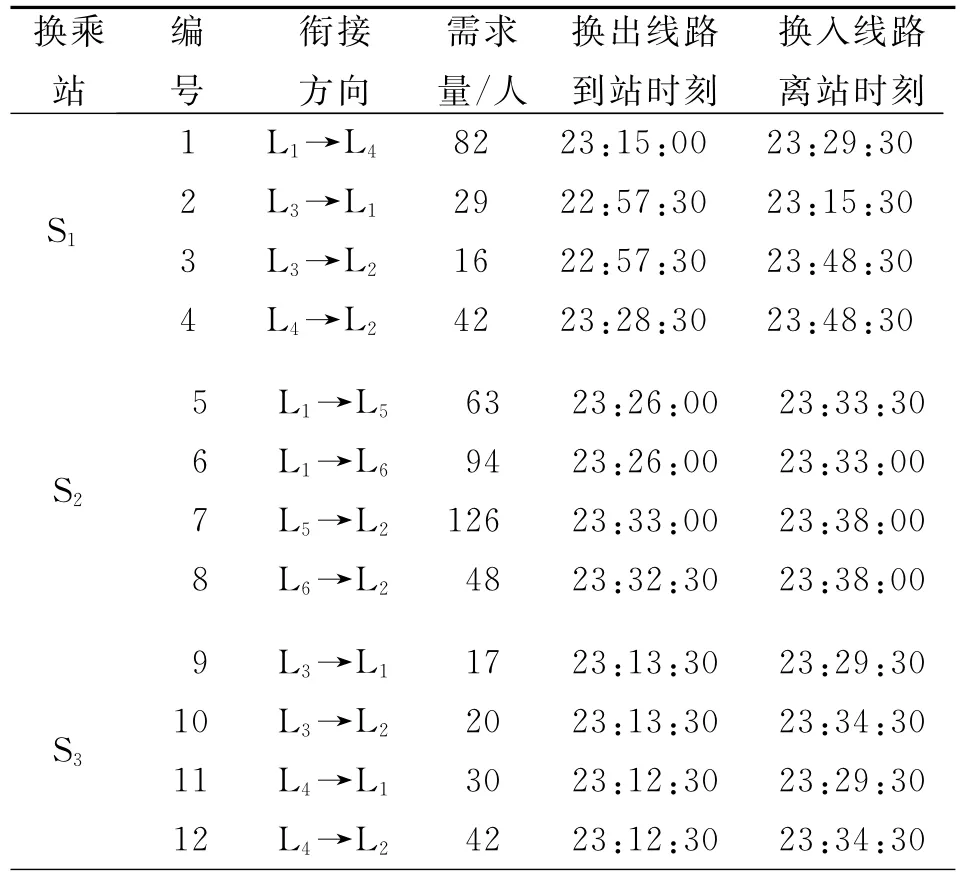
表5 单个换乘方向约束下末班车发车时刻对应的衔接情况
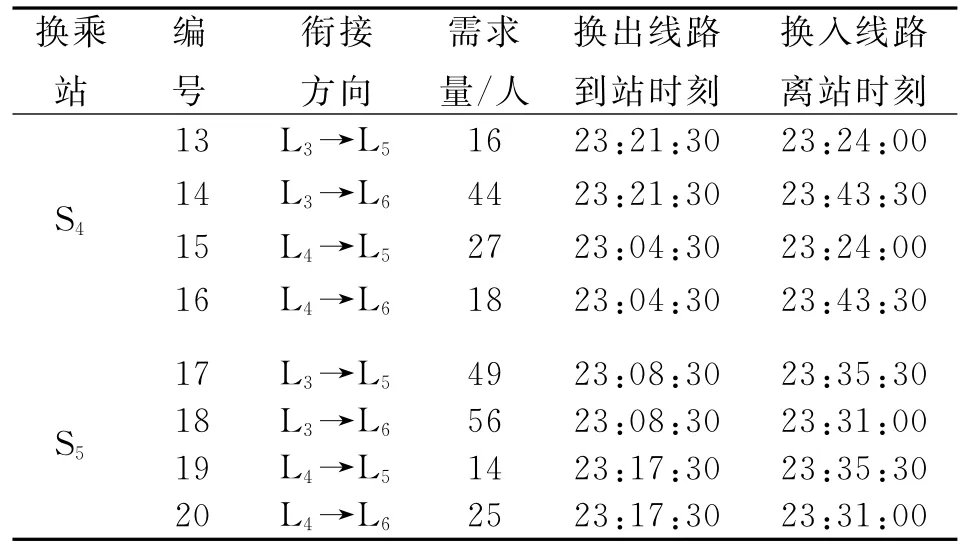
续表5
网络采用原始末班车发车时刻只能衔接19个换乘方向,换乘成功客流量为610人。当对末班车时刻表进行单个换乘方向约束优化后,可衔接20个换乘方向,换乘成功的客流量为858人,优化率达40.66%。改变的衔接关系如图7所示。
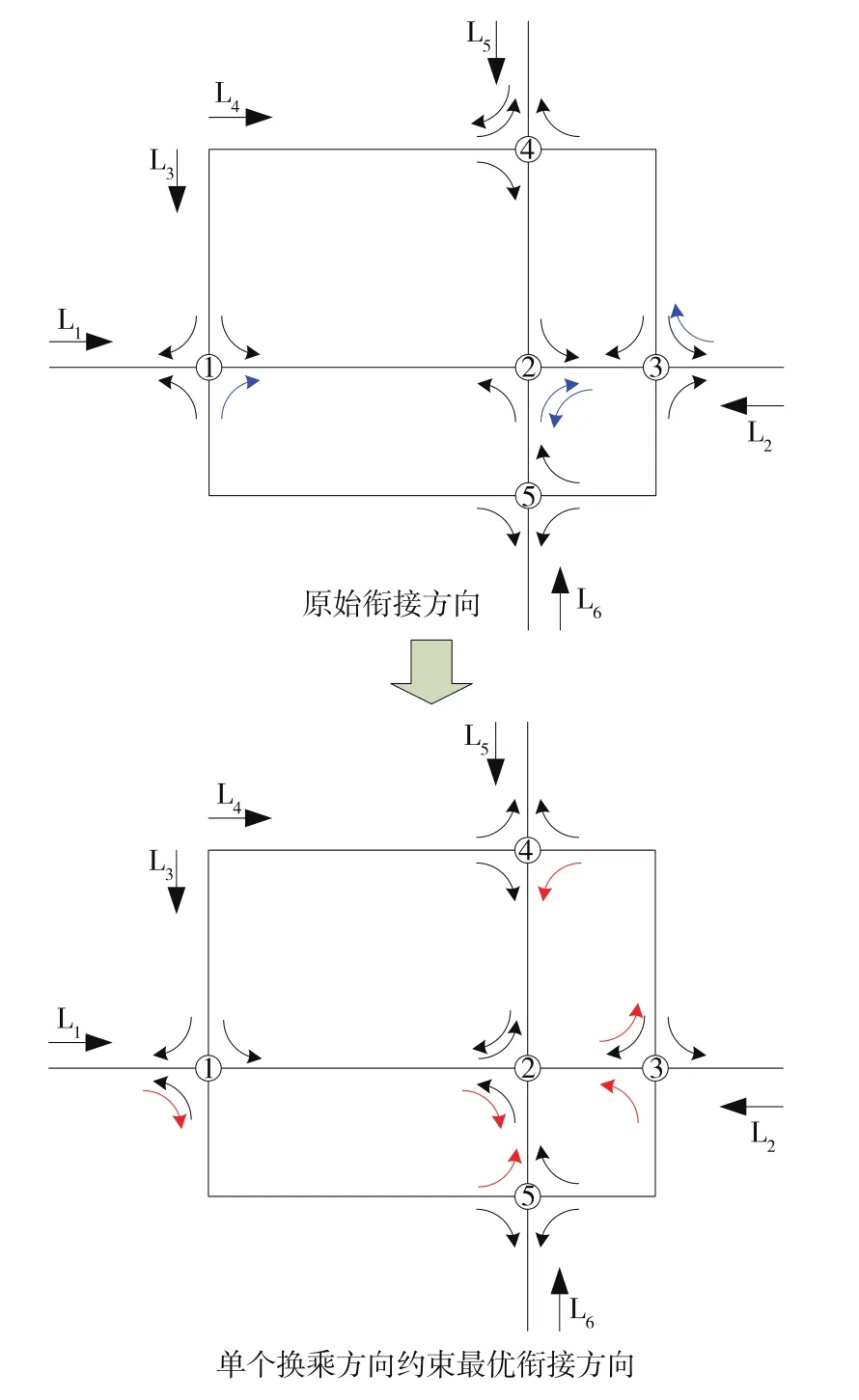
图7 单个换乘方向约束下衔接方向图
5 结语
随着城市轨道交通线路数量的增加,城市轨道交通网络逐步形成,原本的轨道交通单线运营组织模式难以适应网络化运营需求。在实际运营中,由于各条线路末班车运营时间没有承接性,经常发生乘客无法经换乘抵达目的站的现象,且对于一些换乘站末班车衔接预留的换乘时间不足,导致部分乘客换乘失败。该文分析了换乘站列车流与换乘客流的到发顺序关系,进而分析了换乘站内末班车衔接过程的特殊性。针对城市轨道交通网络末班车,建立了考虑特定换乘方向的网络末班车时刻表衔接模型,并设计遗传算法对模型求解。根据该模型和算法可得到满足特定方向换乘情况下的网络整体最优末班车衔接时刻表,对协调网络中末班车的衔接具有重要现实意义。
该考虑特定换乘方向的网络末班车时刻表模型是建立在假设各换乘站间的行驶时间不变的前提下的,而在实际运营过程中,列车运行延误的情况经常发生,针对存在延误情况下末班车时刻表的调整还有待深入研究。
[1] A Ceder,B Golanyb,O Talb.Creating bus timetables with maximalsynchronization[J].Transportation Research Part A:Policy and Practice,2001,35(10).
[2] Chung E-H,A Shalaby.Development of a controlstrategy for inter-modal connection protection of timedtransfer transit routes[R].Transportation Research Record,2006.
[3] Shafahi Y,Khani A.A practical model for transfer optimization in a transit network:model formulations andsolutions[J].Transportation Research Part A: Policy and Practice,2010,44(6).
[4] Chowdhury M S,Chien S I J.Dynamic vehicle dispatching at intermodal transferstation[R].Transportation Research Record,2001.
[5] Guihaire V,HAO J-K.Improving timetable quality inscheduled transit networks[A].Trends in Applied Intelligent Systems[C].2010.
[6] Alessandro chierici,Roberto Cordone.The demand-dependent optimization of regular train timetables[J].E-lectronic Notes in Discrete Mathematics,2004,17.
[7] 房霄虹.城市轨道交通网络化运输组织协调理论及方法研究[D].北京:北京交通大学,2010.
[8] 张铭,徐瑞华,江志彬,等.轨道交通网络列车衔接组织的递阶协调优化[J].系统工程,2007,25(9).
[9] 罗钦,徐瑞华.基于运行图的轨道交通网络动态可达性研究[J].同济大学学报:自然科学版,2010,38(1).
[10] 徐瑞华,张铭,江志彬.基于线网运营协调的城市轨道交通首末班列车发车时间域研究[J].铁道学报,2008,30(2).
[11] 白广争,郭进.基于离站时刻协调的地铁换乘站列车衔接优化研究[J].交通运输系统工程与信息,2013,13(5).
[12] 赵鹏,张秀媛,孙晚华,等.管理运筹学教程[M].第二版.北京:清华大学出版社,2014.
[13] 陈团生,毛保华,何宇强.旅客列车发车时间域优化研究[J].铁道学报,2006,28(4).
[14] 马超云.城市轨道交通换乘站列车时刻表的协调和优化[D].北京:北京交通大学,2010.
U492.2
A
1671-2668(2016)05-0042-07
2016-02-24

