基于多层统计模型的城市快速路汇入区通行能力影响因素分析

刘好德，郑进炫，孙剑，杜荣华

（1.交通运输部科学研究院，北京 100029；2.同济大学交通运输工程学院，上海 201804；3.长沙理工大学智能交通与车路协同技术研究所，湖南长沙 410076）

基于多层统计模型的城市快速路汇入区通行能力影响因素分析

刘好德1，郑进炫2，孙剑2，杜荣华3

（1.交通运输部科学研究院，北京 100029；2.同济大学交通运输工程学院，上海 201804；3.长沙理工大学智能交通与车路协同技术研究所，湖南长沙 410076）

为了探究城市快速路汇入区通行能力及其影响因素，选取2011年上海市快速路111个汇入区交通流检测数据，根据速度-流量曲线确定8个可获得实测通行能力的有效汇入区瓶颈点，利用15min最大小时流率法计算汇入区通行能力，然后基于多层统计模型，综合考虑静态与动态影响因素，构建了汇入区通行能力估计模型，检验结果显示其估计误差仅2.6%，可准确估计城市快速路汇入区通行能力；最后以模型结果为依据，提出了快速路通行能力影响因素修正系数，并与美国HCM2010、中国《公路通行能力分析细则》及相关研究资料进行了对比分析。

城市交通；城市快速路；汇入区；多层模型；通行能力

汇入区是城市快速路系统的重要组成部分，通常定义为两股或多股车流汇合成一股车流的路段。由于大量车辆汇入，交通流极易受到干扰，常形成常发性拥堵瓶颈。遗憾的是中国还未提出较为完整的汇入区通行能力估计模型。由于中国城市快速路与高速公路设施设计、交通组成及驾驶行为等方面的差异，直接参考国外研究成果可能导致较大的应用误差。同时国内现有关于通行能力的研究大多是在有限观测条件下获得的有限样本基础上进行的，鲜有基于大量实测数据分析通行能力影响因素并建立估计模型。随着中国交通信息化的建设，城市快速路已建立了完善的交通流检测系统，基于海量交通流数据获取大量实测通行能力样本已成为可能。该文基于大量快速路实测数据，在分析汇入区影响因素的基础上构建汇入区通行能力多层统计分析模型，为城市快速路规划、设计与运行管理提供理论支持和技术支撑。

1 研究综述

通行能力影响因素一直以来都是通行能力领域的研究重点。在以往的研究中，通行能力影响因素通常包括道路条件、交通条件、环境条件与管理控制条件等。根据静态与动态的观点，通行能力影响因素可分为两类：一类是面向规划设计的静态影响因素；另一类是面向管理控制的动态影响因素。

在静态通行能力影响因素研究方面，HCM2010提出了车道宽度、侧向净空、匝道密度、纵向坡度、地形、速度等道路条件与管理控制条件对通行能力的影响；Chandra S.等利用回归分析方法研究了车道宽度因素，提出通行能力随车道宽度的增大而增大；温学钧基于回归分析方法研究城市快速路通行能力，指出通行能力与车道宽度存在二次函数关系；钟连德等采用对比分析方法确定城市快速路基本路段通行能力，提出了不同车道的通行能力修正系数；胡章立利用层次分析法，研究了包含道路、交通与环境在内的20个影响因素，得到各因素对通行能力影响的相对权重；茹红蕾基于对比分析与回归分析方法，提出通行能力随车道数的增加而降低、通行能力与车道宽度和主线段长度均符合三次函数、路段S线形对上游通行能力影响非常明显等结论。

在动态通行能力影响因素研究方面，HCM2010提出了交通组成、驾驶员组成、恶劣天气、星期特性、道路施工等交通条件与环境条件对通行能力的影响；Ibrahim A.T.等利用对比分析方法对恶劣天气展开研究，提出大雨与大雪天气分别导致最大流率降低10%～20%与30%～48%；Brilon W.等对比分析了日夜、路面湿度与星期特性对通行能力的影响，得到了不同条件下通行能力折减比例；Agarwal M.等通过对比分析，提出了不同降雨/雪强度下通行能力折减比例；胡章立应用层次分析法，得到了交通与环境因素对通行能力影响的相对权重；杨忠良等通过对比分析，提出了恶劣天气下通行能力折减系数。

综上所述，目前关于通行能力影响因素的研究既有专门针对静态因素，也有特地针对动态因素，在研究方法上则大多采用对比分析与回归分析得到通行能力修正系数，缺乏从统计学视角的动静态影响因素的统筹研究。因此，该文针对城市快速路，进行系统、综合考虑静态因素与动态因素的通行能力影响因素分析。

2 数据准备

2.1交通流数据来源

数据来源于2011年上海市快速路感应线圈检测数据，检测参数包含以车道为基础的分车型流量、分车型速度与占有率，数据采集间隔为5min。根据HCM2010关于汇入区的定义，选取上海市快速路111个汇入区作为研究对象。根据研究需要，选点感应线圈检测数据必须完整并达到通行能力状态，经过严格筛选，有效汇入区瓶颈仅8个，其几何布置见图1～8。

图1 瑞金南路汇入区瓶颈点（NHNX10）几何布置（单位：m）

图2　五一路汇入区瓶颈点（NHNX32）几何布置（单位：m）

图3　宛平南路汇入区瓶颈点（NHWX12）几何布置（单位：m）

图4　吴中路汇入区瓶颈点（NHWX21）几何布置（单位：m）

图5　武宁路汇入区瓶颈点（NHWX38）几何布置（单位：m）

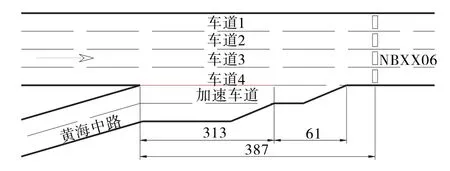
图6　黄海中路汇入区瓶颈点（NBXX06）几何布置（单位：m）

图7　虹许路汇入区瓶颈点（YANX08）几何布置（单位：m）

图8　江苏路汇入区瓶颈点（YANX21）几何布置（单位：m）

2.2变量采集

对于实测通行能力的估计，采取最大值选择法（15min最大小时流率）。该方法与HCM2010关于通行能力的定义取值一致，在交通运输领域得到广泛认可。

参考HCM2010、《公路通行能力分析细则》、相关研究资料与工程经验，结合上海市快速路自身特点，选取10余个可能影响因素作为自变量进行分析（见表1）。其中：车道数、车道宽度、侧向净空、平曲线曲率、汇入长度等几何设计信息通过设计图纸、电子地图与实地测量得到；天气数据来源于气象部门，由于数据有限，仅分晴、雨、雪三类；对于时段特性，基于上海市快速路高峰时段（7：30—9：30、16：30—18：30）对外地牌照限行的考虑进行高峰与平峰时段划分；车型比例数据通过交通流检测数据得到。

表1　变量说明

3 汇入区通行能力估计模型

通行能力影响因素大致可分为两类：一类针对特定观测点保持不变，如车道宽度、车道数等在短时间内无法改变，称为静态因素；另一类则动态变化，如天气、车型比例等，称为动态因素。相比于传统回归分析数据，该文研究中采用多个观测点多天数据，即针对一个观测点，车道数与车道宽度是一样的，而天气与车型比例等有数百条，正是由于这种数据结构特点，不同观测点间的通行能力可能存在差异，传统的回归分析模型不再适用。为此，采用多层统计分析方法构建汇入区通行能力模型。

3.1多层统计分析模型

多层统计分析模型所分析的多层数据不仅包括在微观水平观察到的信息，也包括从宏观角度得到的数据，可用于纵向数据处理。所谓纵向数据是指对同一批个体对象进行多次重复测量所获得的数据，这类数据可看作是多层数据，其中重复测量嵌套在个体对象中。在多层模型分析中，被解释变量是在个体水平测量的变量；而解释变量既在个体水平，也在组群水平测量。为简便起见，下面是在一个两水平多层模型中包括两个水平1解释变量和一个水平2解释变量：

式中：yij表示在第j个水平2单位（如第j个检测点）中的第i个个体的水平1结局测量；i=1，2，…，N；N为总样本量；j=1，2，…，J；J为水平2的单位数。

绣襦香风阵阵来，粉红衣裳荷花裁，巧笑盈盈，牵着大鹏小鲲，站在抱日台暖黄朝阳中等候着湿淋淋如水老鼠般依次由落星湖中钻出来的四个人的，不是花圣宇晴，却是谁？可站在她身边，长身危立，紫襦黑衣，面如白玉，黑须漆漆，一手拈须，四十开外，沉静如水的中年男子，他是谁？他高大的身形为什么这么眼熟，这位大叔，好像在哪里见过……

从概念上讲，可把两水平多层模型看作是通过两个步骤进行估计的：第一步，分别在每个水平2观察单位中进行水平1观察的回归运算，即同样的回归模型在J个组群中运算J次，产生J组回归系数，组成J个水平1截距和斜率的数据集。第二步，将水平1随机回归系数看成是某些水平2变量（如ωij）的函数，生成水平2方程或宏观模型。

将式（2）和式（3）代入式（1），得：

式（4）是一个组合模型或复合模型，是多层模型的单一公式表述。该模型看起来与带有一个交互作用项的普通回归模型有些相似，但与固定效应模型不同，该模型具有一个符合残差的结构，即式（4）中括弧内的各项，包括水平2误差项u0j和u1j、水平1误差项及水平1解释变量z1ij。需注意的是，水平2误差项u0j和u1j的下标不是“ij”，而只有“j”，表示其值在各组群内并没有变化，只是在组间有变化。换而言之，各组内的观察值共同分享非解释性水平2随机变异，因而各组内观测值互补独立。

3.2相关性检验

为了保证多层统计分析模型回归的有效性，避免出现共线性问题，对解释变量进行spearman相关性检验。备选的解释变量有汇入长度ml、车道数n、车道宽度lw、左侧侧向净空llc、右侧侧向净空rlc、匝道密度rd、平曲线曲率cur、星期特性w、时段特性pd、天气特性wer、大车比例lv及中车比例mv等，spearman相关性检验结果见表2。

表2　spearman相关性检验结果

从表2来看，车道宽度lw和左侧侧向净空llc、右侧侧向净空rlc与平曲线曲率cur的相关度很高，汇入长度和匝道密度rd也高度相关。为确保模型的准确性，选用车道宽度与汇入长度而放弃另外4个变量进行模型构建，然后把自变量分为两层，汇入长度、车道数与车道宽度为一层，星期特性、时段特性、天气、大车比例与中车比例为另外一层。

3.3模型结果

基于SAS数据分析软件对备好的分层数据进行多层统计分析模型构建，模型形式如下：

式中：工作日w=1，反之w=0；天气为晴时sun= 1，反之sun=0；天气为雨时rain=1，反之rain=0；通行能力在6：00—7：30达到时p1=1，反之p1= 0；通行能力在7：30—9：30达到时p2=1，反之p2=0；通行能力在9：30—10：30达到时p3=1，反之p3=0；通行能力在10：30—16：30达到时p4=1，反之p4=0；通行能力在16：30—18：30达到时p5= 1，反之p5=0；通行能力在18：30—19：30达到时p6=1，反之p6=0。

为了验证汇入区通行能力多层统计模型的有效性，对模型估计值与实测值进行对比分析（见图9）。由图9可知：通行能力估计值与实测值非常接近，估计误差平均值仅为2.6%，表明多层统计模型能很好地估计汇入区通行能力。

图9　汇入区通行能力多层统计模型检验结果

4 通行能力影响因素分析

4.1修正系数建议值

为了方便交通工程人员估计快速路汇入区通行能力，基于多层统计回归模型结果对通行能力影响因素模型中的系数作进一步整理分析。汇入区基本通行能力取2 300 veh/（h·车道），以该值为基准，得到通行能力影响因素修正系数（见表3～10）。

表3　车道数修正系数

表4　车道宽度修正系数

表5　汇入长度修正系数

表6　星期特性修正系数

表7　时段修正系数

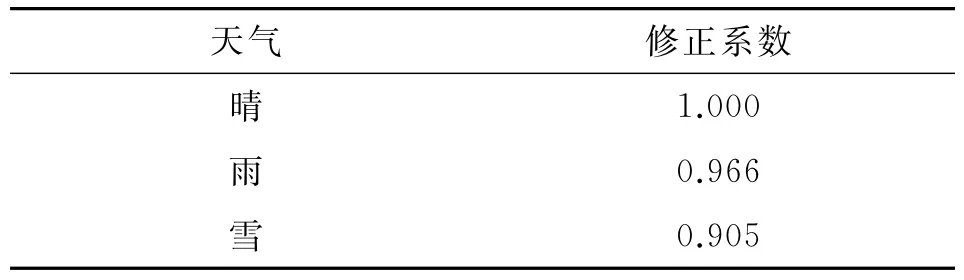
表8　天气修正系数

表9　大车比例修正系数

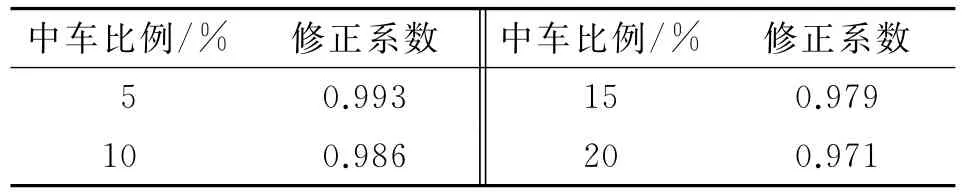
表10　中车比例修正系数

4.2影响因素分析

为了进一步探讨通行能力影响因素修正系数的准确性，与HCM2010、《公路通行能力分析细则》及过去研究成果进行对比分析。

（1）车道数。HCM2010中没有明确提出车道数对通行能力的影响；《公路通行能力分析细则》中规定了车道数对自由流速度的影响，车道数越少，自由流速度越低。由于通行能力与自由流速度存在一定关系，车道数越少，通行能力越低。根据多层统计分析模型结果，通行能力随车道数的增加而降低，该趋势与HCM2010和《公路通行能力分析细则》相反，但与茹红蕾的研究成果一致。

（2）车道宽度。根据多层统计分析模型的分析结果，车道宽度对通行能力存在正影响，该结果与HCM2010及《公路通行能力分析细则》相一致。HCM2010中针对施工区提供了专门的车道宽度修正系数（见表11）。对比文中修正系数与HCM2010修正系数，文中修正系数总体上大于HCM2010，以2.75～3.00m为例，HCM2010的车道宽度修正系数为0.86，文中为0.975～0.981，远高于HCM2010修正系数推荐值。

表11　HCM2010车道宽度修正系数

（3）工作日特性。模型结果显示，汇入区工作日通行能力比非工作日高72 veh/（h·车道），工作日通行能力明显高于非工作日。根据HCM2010，工作日与非工作日汇入区通行能力差值为109～188 veh/（h·车道）。对比国内外数据，中国工作日与非工作日通行能力差值略低于国外研究值，但研究结果均体现了驾驶员总体特征的影响，鉴于工作日多数是通勤交通，驾驶员总体上技术更熟练，也更熟悉行驶路段，因而通行能力高于非工作日。

（4）天气特性。许多研究表明恶劣天气对通行能力具有显著影响。上海监测数据显示在恶劣天气情况下，雨天通行能力折减3.4%，雪天通行能力折减9.5%。表12为HCM2010研究结果，对比可知上海雨天通行能力折减比例在HCM2010低降雨强度范围内，雪天通行能力折减比例在中等降雪强度范围内，与HCM2010大体一致。由于上海研究数据没有详细的降雨/降雪强度，在通行能力估计时可结合降雨/降雪实际情况借鉴HCM2010的成果。

表12　HCM2010恶劣天气通行能力折减

（5）时段特性。从时段特性回归结果可知早高峰时段（6：00—7：30，7：30—9：30）与晚高峰时段（16：30—18：30）的通行能力修正系数明显高于其他时段，可能由两方面原因造成：一是上海快速路高峰时段禁止外地牌照车辆通行；二是高峰时段主要由通勤交通组成，与平峰时段交通组成存在差异。这两方面因素促使高峰时段与平峰时段间的驾驶员特征不同，造成两时段通行能力存在差异。

（6）中车比例与大车比例。在HCM2010与《公路通行能力分析细则》中，中车与大车对通行能力的影响均通过交通组成修正系数来实现，计算公式见式（6）。通常，上海快速路达到通行能力时最大通过量高于1 600veh/（h·车道），参考《公路通行能力分析细则》中的车辆折算系数（见表13），中型车与大型车分别取2.5与4.0。HCM2010中未针对车型进行详细划分，大型车与中型车折算系数均取1.5。表14为文中研究、中国公路通行能力手册（简称CHCM2015）与HCM2010修正系数值对比，从中可见文中研究所得大型车与中型车修正系数均大于HCM2010与CHCM2015，与HCM2010更为接近，但远高于CHCM2015。此外，大型车修正系数与HCM2010差值较小，中型车修正系数差值较明显，这可能是由于美国只考虑货车和巴士车辆，而上海城市快速路禁止货车通行，中型车基本为中型客车，故中型车修正系数较高，对通行能力影响较小。

式中：fHV为交通组成修正系数；pi为道路上车型i的交通量占总交通量的百分比；Ei为车型i的车辆折算系数。

表13　《公路通行能力分析细则》中的车辆折算系数

表14　交通组成修正系数比较

（7）汇入长度。HCM2010与《公路通行能力分析细则》都没有提出汇入长度对通行能力的影响。根据文中研究结果，通行能力随汇入长度的减小而降低，说明提供足够的加速段给车辆汇入可促进交通更高效地运行。

5 结论

（1）综合考虑静态与动态影响因素的多层统计分析模型估计误差仅为2.6%，能很好地估计城市快速路汇入区的通行能力。

（2）基于多层统计分析模型结果提出通行能力修正系数，包含汇入长度、车道数、车道宽度、星期特性、时段特性、天气特性及交通组成等因素，可为通行能力手册中通行能力修正系数修正提供参考。

（3）在多层统计分析模型研究中，一些通行能力影响因素之间存在高度相关性，为了保证模型回归的准确性，对这些影响因素进行了一定取舍。进一步研究建议扩大样本量，对所有可能影响因素进行回归建模，分析其对通行能力的影响程度。

［1］ Transportation Research Board.Highway capacity manual 2010［R］.Transportation Research Board，2010.

［2］ Chandra S，Kumar U.Effect of lane width on capacity under mixed traffic conditions in India［J］.Journal of Transportation Engineering，2003，129（2）.

［3］ 温学钧.上海城市快速路通行能力的研究［J］.上海建设科技，2005（1）.

［4］ 钟连德，李秀文，荣建，等.城市快速路基本路段通行能力的确定［J］.北京工业大学学报，2006，32（7）.

［5］ 胡章立.快速路基本路段通行能力影响因素研究［D］.长沙：长沙理工大学，2007.

［6］ 茹红蕾.城市道路通行能力的影响因素研究［D］.上海：同济大学，2008.

［7］ Ibrahim A T，Hall F L.Effect of adverse weather conditions onspeed-flow-occupancy relationships［J］. Transportation Research Record，1994，1457.

［8］ Brilon W，Ponzlet M.Auswirkungen von zeitlich veraenderlichen leistungsfahigkeiten：schlussbericht［R］. Lehrstuhl fur Verkeshrswesen，Ruhr Universitat Bochum，1995.

［9］ Agarwal M，Maze T H，Souleyrette R.Impacts of weather on urban freeway traffic flow characteristics and facility capacity［A］.Proceedings of the 2005 Mid-continent Transportation Research Symposium［C］.2005.

［10］ 杨中良，林瑜，高霄.恶劣天气条件下城市快速路通行能力研究［J］.交通信息与安全，2010，28（1）.

［11］ 周荣贵，荣建.公路通行能力分析细则［R］.北京：交通运输部科学研究院，2015.

U491.2

A

1671-2668（2016）05-0016-06

2016-05-17