一个新四维超混沌系统的构建与电路实现
朱 雷, 刘艳云, 王 轩, 武花干, 周小勇
(1.江苏理工学院 电气信息工程学院, 江苏 常州 213001; 2.南京航空航天大学 电子信息工程学院, 南京 210016;3.常州纺织服装职业技术学院 机电工程系, 江苏 常州 213164; 4.南京理工大学 电子工程系, 南京 210094)
一个新四维超混沌系统的构建与电路实现
朱 雷1,2*, 刘艳云3, 王 轩1, 武花干4, 周小勇1
(1.江苏理工学院 电气信息工程学院, 江苏 常州 213001; 2.南京航空航天大学 电子信息工程学院, 南京 210016;3.常州纺织服装职业技术学院 机电工程系, 江苏 常州 213164; 4.南京理工大学 电子工程系, 南京 210094)
利用基本Sprott-B系统仅具有两个涡卷平衡点的特点,通过系统改造与推广,提出一个具有3个平衡点的三维混沌系统,进而通过增加一维线性控制器并反馈至三维系统状态方程,构建出一个新四维超混沌系统.采用相轨图、Lyapunov指数谱和分岔图等动力学工具对超混沌系统进行了仿真分析.结果表明,当参数变化时,系统可以在周期或复杂周期、混沌与超混沌之间演变,存在复杂而奇异的动力学行为.研制电子电路并生成了超混沌吸引子,完成了实验验证.
超混沌系统; 平衡点; Lyapunov指数谱; 电路实现
由于超混沌系统具有两个或两个以上的正Lyapunov指数,因而比混沌系统具有更为复杂的动力学行为,从而在保密通信等工程技术领域具有重要的应用价值[1].长期以来学术界对于超混沌系统的研究与发掘从未停歇,在三维混沌系统状态方程上加载不同的反馈控制器构造四维或更高维的系统,成为一种有效的探索手段.文献[2]和文献[3]分别从Chua系统和Colpitts振荡器模型出发,添加反馈控制器并引入分段线性函数,构造并物理生成了相应的多涡卷超混沌吸引子.
除上述从电子电路原型中抽象出的混沌系统以外,更多的研究焦点集中在具有对称蝴蝶混沌吸引子的三维连续混沌系统上.2007年,王光义等学者通过对Lorenz系统施加线性反馈控制器,实现并电路生成了两翼超混沌吸引子[4];2009年,包伯成等提出一个新三维混沌系统,即Bao系统[5],并利用线性反馈控制得到相应的超混沌系统[6];2010年,贾立新等通过对Chen系统进行线性反馈控制,得到一种超混沌Chen系统[7];包伯成等通过对增广Lü系统进行线性反馈控制,得到一个四翼蝴蝶超混沌系统[8];2012年,李春来与禹思敏通过对Yang系统的三个状态方程同时施加线性控制器,构建了一种超混沌系统并完成电路实验验证[9];2014年以来,新的超混沌系统依然在陆续出现[10,11].
作为三维连续混沌系统,基本Sprott-B系统[12]由美国学者Sprott于1994年提出,相关的研究报道较少,文献[13]和[14]基于其数学模型分别构建了两种不同的分段线性混沌系统.从相轨图角度看,基本Sprott-B系统具有两翼蝴蝶混沌吸引子,从平衡点角度看,与上文提到的三维两翼蝴蝶混沌系统不同,仅具有两个涡卷平衡点,从这个差别出发,本文尝试对基本Sprott-B系统进行改造,从而提出一个具有3个平衡点的新三维混沌系统,并进一步构建出一个新四维超混沌系统,同时搭建电子电路验证并观察系统生成的两翼蝴蝶超混沌吸引子.
1 新四维超混沌系统的构建
基本Sprott-B混沌系统[12]状态方程为:

(1)
与其它典型连续混沌系统如Lorenz系统等相同的是,系统(1)具有一对指标2的鞍焦平衡点S1=(1, 1, 0)和S-1=(-1,-1, 0),从而呈现出一个两翼蝴蝶混沌吸引子.不同的是,系统(1)缺少一个指标1的鞍点.而从目前四维连续蝴蝶超混沌系统构建的角度来看,一般都是基于现有三维连续混沌系统,通过引入一维线性或非线性控制器并反馈至三维系统方程中获得,大多数情况下,原三维系统中指标1的鞍点对应于四维超混沌系统中唯一的不稳定平衡点,并往往成为生成超混沌吸引子的关键.
基于上述思想,本文首先对系统(1)进行一种巧妙地改进,在第3个方程中增加一个线性项-z,并引入正参数a, b, c进行系统推广,从而提出一个新的三维混沌系统,其数学模型为:

(2)

图1 系统(2)的混沌吸引子Fig.1 Chaotic attractor of system (2)

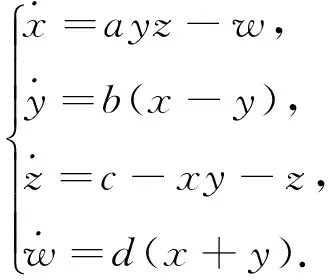
(3)
式中参数,a, b, c, d均大于0,当取参数a=10, b=4, c=1, d=0.5时,系统表现出两翼蝴蝶超混沌吸引子,如图2所示.此时系统(3)的四个Lyapunov指数为LE1=0.1452, LE2=0.1013, LE3=0.0014, LE4=-5.2478,其Lyapunov维数为dL=3.047,因此系统处于超混沌状态.下面对其动力学特性进行详细的分析.

图2 系统(3)的超混沌吸引子Fig.2 Hyperchaotic attractor of system (3)
2 超混沌系统的动力学分析
2.1 基本动力学分析
对于系统(3),满足
.
(4)
因此系统(3)耗散.代数计算可知,系统(3)仅有一个平衡点E0=(0, 0, c, 0),在E0处线性化系统(3),得其Jacobi矩阵

(5)
以及相应的特征多项式
f(λ)=(λ+1)g(λ),
(6)
式中,
g(λ)=λ3+bλ2+(d-abc)λ+2bd.
(7)
对于g(λ),根据Routh-Hurwitz判据,由于-bd-ab2c<0,所以E0是不稳定平衡点.展开(6)式,得到
f(λ)=λ4+(b+1)λ3+(b+d-abc)λ2+
(d+2bd-abc)λ+2bd.
(8)
当取参数a=10, b=4, c=1, d=0.5时,数值计算得到四个特征根λ1=-8.6305,λ2=4.5281,λ3=-1,λ4=0.1024,因此平衡点E0为不稳定的鞍点.
2.2 Lyapunov指数谱和分岔图
系统参数变化,动力学行为将随之发生改变,下面从Lyapunov指数谱和分岔图的角度动态观察这一影响.限于篇幅,这里仅分析参数b和d变化对系统的影响,且为了图形清晰起见,这里忽略了第四根负Lyapunov指数LE4.
固定参数a=10, c=1, d=0.5,改变参数b,当b∈[0.1,20]时,数值仿真得到系统(3)的Lyapunov指数谱和分岔图,如图3所示.这里x-b分岔图仿真时选择的Poincaré截面为z=0平面.从图3可见,随着b的改变,系统状态在周期或复杂周期、混沌与超混沌之间演变.当b∈[0.1,0.7)时,Lyapunov指数LE1=0, LE2, LE3, LE4< 0,系统处于周期或复杂周期状态;当b∈[0.7,1.5)时,除在b=1.22处存在一个周期窗口以外,Lyapunov指数LE1> 0, LE2=0, LE3, LE4< 0,系统处于微弱的混沌状态;当b∈[1.5,2.3)时,Lyapunov指数LE1=0, LE2, LE3, LE4< 0,系统处于周期状态;当b∈[2.3,2.6)时,Lyapunov指数LE1 > 0, LE2=0, LE3, LE4<0,系统处于混沌状态;当b∈[2.6,11.3)时,Lyapunov指数LE1> 0, LE2> 0, LE3=0, LE4< 0,系统处于超混沌状态;当b∈[11.3,20]时,除个别瞬态、微弱的混沌窗口以外,Lyapunov指数LE1=0, LE2, LE3, LE4< 0,系统处于周期状态,且为周期3.

图3 b变化时系统(3)的Lyapunov指数谱和分岔图Fig.3 Lyapunov exponent spectrum and bifurcation diagram with changing b of system (3)
固定参数a=10, b=4, c=1,改变参数d,当d∈[0.1,1.6]时,数值仿真得到系统(3)的Lyapunov指数谱和分岔图,如图4所示.这里z-d分岔图选择的Poincaré截面为y=1平面.显而易见,当d∈[0.1,1.06)时,除个别混沌窗口外,Lyapunov指数LE1> 0, LE2> 0, LE3=0, LE4< 0,系统处于超混沌状态;当d∈[1.06,1.6]时,除个别瞬态混沌窗口以外,Lyapunov指数LE1=0, LE2, LE3, LE4< 0,系统处于周期状态.进一步的相轨图仿真研究表明,当1.06 ≤ d < 1.4时,系统呈现出单翼周期吸引子,当1.4 ≤ d ≤ 1.6时,呈现出对称两翼周期吸引子.且在单翼周期区域中,隐藏着局部的吸引子共存窗口,例如,当d=1.1时,参数初值(x0, y0, z0, w0)分别为(1, 1, 1, 1)和(1, 1, 1,-1)时,分别对应着右吸引子和左吸引子.
3 电路实现与实验验证
根据系统(3)的微分方程组,可以设计并制作硬件实现电路,如图5所示.这里τ=R0C0为积分电路时间常数,也是时间尺度变换因子,为了保证实验观测效果,取R0=100 kΩ,C0=0.1 μF,从而电路生成的超混沌信号在相轨图不变的情况下,时间域被压缩100倍.为了保证电路实现精度,集成运算放大器和模拟乘法器分别选择了TI公司的TL084和MPY634集成芯片,并采用±12 V线性电源电压供电,电阻采用了多圈电位器精密调节得到,而电容则采用大量CBB电容精密测量筛选获得.
当取电阻Ra=2 kΩ,Rb=5 kΩ,Rd=40 kΩ,电压-5c V为-5 V时,对应于系统(3)的参数a=10,b=4,c=1,d=0.5.采用高分辨率的安捷伦数字示波器DSO7054B进行实验观测,可以精密捕获超混沌系统的相轨迹,实验结果如图6所示.通过与图2对比可以发现,电路工作后得到的超混沌吸引子与数值仿真结果保持一致,上述电路可以准确实现本文所构建的超混沌系统.

图4 d变化时系统(3)的Lyapunov指数谱和分岔图Fig.4 Lyapunov exponent spectrum and bifurcation diagram with changing d of system (3)

图5 超混沌系统(3)的电路实现Fig.5 Circuit implementation of hyperchaotic system (3)

图6 超混沌系统(3)的电路实验结果Fig.6 The circuit experimental results of hyperchaotic system (3)
4 结论
本文从仅具有两个涡卷平衡点的基本Sprott-B混沌系统出发,巧妙地在第3个方程中增加一个线性项-z,并引入正参数进行系统推广,提出一个具有3个平衡点的新三维混沌系统,新混沌系统与基本Sprott-B系统具有不同的拓扑结构与混沌吸引子.在此基础上,引入线性控制器w并反馈至新三维混沌系统的第一个方程,从而构建出一个新四维超混沌系统,典型参数下的Lyapunov指数计算表明系统处于超混沌状态,而相轨图仿真表明系统具有两翼蝴蝶超混沌吸引子.在对系统的耗散性、平衡点稳定性分析的基础上,结合Lyapunov指数谱和分岔图等动力学分析手段对系统参数的影响进行了详细分析,结果表明,参数b的变化可以导致系统状态在周期或复杂周期、混沌与超混沌之间演变,参数d的变化可以导致系统状态在周期与超混沌之间演变,且在单翼周期区域中,隐藏着局部吸引子共存窗口.在理论分析和仿真研究的基础上,设计了相应的硬件电路并进行了实验验证,通过对超混沌吸引子的观察,证实了本文所提出的新四维超混沌系统是一个物理可实现的系统.
[1] 瞿少成, 刘 娣, 陈 婵. 基于超混沌Lorenz系统同步控制的保密通信[J]. 计算机工程, 2011, 37(20): 69-70.
[2] XI H L, YU S M, ZHANG C X. Generation and implementation of hyperchaotic Chua system via state feedback control[J]. International Journal of Bifurcation and Chaos, 2012, 22(5): 1250119(1-11).
[3] 包伯成, 刘 中, 许建平. 基于Colpitts振荡器模型生成的多涡卷超混沌吸引子[J]. 物理学报, 2010, 59(3): 1540-1548.
[4] 王光义, 郑 艳, 刘敬彪. 一个超混沌Lorenz吸引子及其电路实现[J]. 物理学报, 2007, 56(6): 3113-3120.
[5] 包伯成. 混沌电路导论[M]. 北京:科学出版社,2013.
[6] BAO B C, LIU Z, XU J P. New chaotic system and its hyperchaos generation[J]. Journal of Systems Engineering and Electronics, 2009, 20(6): 1179-1187.
[7] JIA L X, DAI H, HUI M. A new four-dimensional hyperchaotic Chen system and its generalized synchronization[J]. Chin. Phys. B, 2010, 19(10): 100501(1-11).
[8] BAO B C, XU J P, LIU Z. Hyperchaos from an augmented Lü system[J]. International Journal of Bifurcation and Chaos, 2010, 20(11): 3689-3698.
[9] 李春来, 禹思敏. 一个新的超混沌系统及其自适应追踪控制[J]. 物理学报, 2012, 61(4): 040504(1-7).
[10] LI C L, XIONG J B, LI W. A new hyperchaotic system and its generalized synchronization[J]. Optik, 2014, 125(1): 575-579.
[11] 王 宏, 马朝华. 一个双参数恒Lyapunov指数的超混沌系统及电路仿真[J]. 华中师范大学学报(自然科学版), 2015, 49(3): 378-382.
[12] SPROTT J C. Some Simple Chaotic Flows [J]. Physical Review E, 1994, 50(2): R647-R650.
[13] 陈建军, 禹思敏. 一个分段Sprott系统及其混沌机理分析[J]. 物理学报, 2009, 58(11): 7525-7531.
[14] 朱 雷, 刘艳云. 一个具有调幅特性的分段线性混沌系统与微控制器实现[J]. 电子器件, 2012, 35(6): 652-656.
Construction and circuit implementation of a new four-dimensional hyperchaotic system
ZHU Lei1,2, LIU Yanyun3, WANG Xuan1, WU Huagan4, ZHOU Xiaoyong1
(1.School of Electrical and Information Engineering, Jiangsu University of Technology, Changzhou, Jiangsu 213001; 2.School of Electronic and Information Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016; 3.Department of Mechanical and Electrical Engineering, Changzhou Textile Garment Institute, Changzhou, Jiangsu 213164; 4.Department of Electronic Engineering, Nanjing University of Science and Technology, Nanjing 210094)
Based on the characteristics of the only two equilibrium points in the basic Sprott-B system, a three-dimensional chaotic system is proposed through system reforming and extension, which possess three equilibrium points. Furthermore, by adding a linear controller and feeding back into the state equation of the three-dimensional system, a four-dimensional hyperchaotic system is constructed. The simulation analysis of the hyperchaotic system is carried out by the dynamics tools of phase portrait, Lyapunov exponent spectrum and bifurcation diagram. The results indicate that the change of the parameters leads the system to evolve between period or complex period and chaos or hyperchaos, with complicated and marvelous dynamics behavior. By developing the electronic circuit, the hyperchaotic attractor is generated and the experiment verification is completed.
hyperchaotic system; equilibrium point; Lyapunov exponent spectrum; circuit implementation
2015-07-25.
国家自然科学基金项目(51277017);江苏省自然科学基金项目(BK2012583);江苏省产学研联合创新资金资助项目(BY2014038-06);江苏省高等学校大学生创新创业训练计划项目(201511463004Z).
1000-1190(2016)02-0206-05
TM132
A
*E-mail: zhuleei@126.com.

