基于熵值法的Goodgrant基金最优分配策略

姜宝胜，吴　飞，张静怡，龚佃选

(1. 华北理工大学 数学建模创新实验室，河北 唐山　063000；2. 华北理工大学 理学院，河北 唐山　063000)

基于熵值法的Goodgrant基金最优分配策略

姜宝胜1，吴飞1，张静怡1，龚佃选2*

(1. 华北理工大学 数学建模创新实验室，河北 唐山063000；2. 华北理工大学 理学院，河北 唐山063000)

Goodgrant基金会是美国的一个慈善组织，它希望通过慈善捐助来提高本科生教育绩效。为了更好的利用这笔资金，需要进行投资策略的研究。首先将所有候选学校用SPSS进行K -均值聚类分析，依据聚类结果分为6类。在相同类别中的学校，用MATLAB中的三角形线性插补法进行缺失数据的填补。然后将13个绩效影响因素归纳为生源质量、学校发展情况、学校及学生财务状况三个一级指标。通过熵值法客观地确定学校绩效评价的权重系数。利用熵值法计算出一级二级指标的权重，进行综合评价。按照评价标准计算出每个学校当前的绩效值，并以此对所有学校进行初步排名。选取排名前十的学校，依据每个学校的绩效值及办学规模确定奖学金金额。

K-均值聚类；熵值法；性插补法；绩效值

本文著录格式：姜宝胜，吴飞，张静怡，等. 基于熵值法的Goodgrant基金最优分配策略[J]. 软件，2016，37（9）：24-26

0　引言

高等教育捐赠是一种常见的慈善捐赠，是美国高校尤其是民办高校的重要收入来源。Goodgrant基金会是一个新的慈善组织，该组织计划每年给符合条件的学校捐赠2亿美元[1]。在对学校进行主观评价时，从整体性能上往往难以进行评价。所以，一般先根据评价系统中的整体特性判断评价指标，而确定各指标权重则结合相应的数学方法，评价指标的最终得分由指标得分和权重确定[2]。在评价方法的选取上常用层次分析法和模糊层次分析法，但这些方法都包含了主观赋值的过程，评价结果受评价者主观意愿影响较大[3]。熵值法是基于信息熵的原理，通过各指标值所提供信息量的大小来确定指标权重，属于客观赋权法。熵值法有效地弥补了层次分析法等方法主观随意性较大的缺陷[4]。因此，本文提出了基于熵值法的学校绩效评价方法，通过熵值法对权重指标进行计算，制定科学的评价标准。

1　数据处理

在收集学校指标数据的过程中，不可避免回出现数据缺失的现象，需要进行缺失数据的填补。由于不同学校的差别很大，根据整体样本数据进行填补的话误差较大，所以要对学校进行分类。本文采用K-均值聚类进行分类[5]。

1.1K-均值算法

1）假设数据样本集的大小为n，设1I=,选取K个初始聚类中心：；如果满足则

2）计算聚类中心到每一个数据样本的距离：

3）进行误差平方和准则函数JC计算：

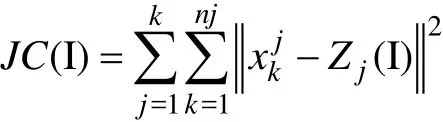
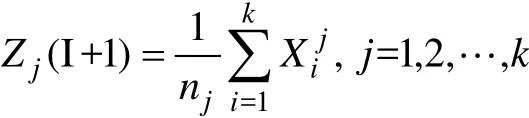
1.2聚类结果

将样本数据进行聚类，分为6类。由于数据量过大只展示部分结果。聚类的结果如图1：

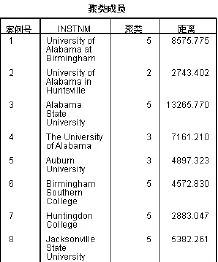
图1　聚类结果

根据聚类结果，在相同类别中的学校，用MATLAB中的三角形线性插补法进行缺失数据的填补。

2　利用熵值法确定指标权重

2.1熵值法进行综合评价的步骤

1）无量纲化处理

将各指标值ijx转化为无单位的相对数ijx＇。计算方法为：对于正向指标对于逆向指标：

第j项指标的信息熵值为：式中常数K和系统样本数m相关。在一个信息完全无序的系统中，其有序度为零，熵值最大，1e=，m个样本处于完全无序分布状态时，，这时

3）指标信息熵值e和信息效用值d的计算[6]。某项指标的信息效用价值取决于该指标的信息熵je与1之间的差值：

2.2评价指标权重的计算

利用熵值法估算各指标的权重,本质上是利用指标信息的价值系数来计算，其价值系数与评价的重要性成正比。最后能够得到第j项指标的权重，为：

权重结果如表1：

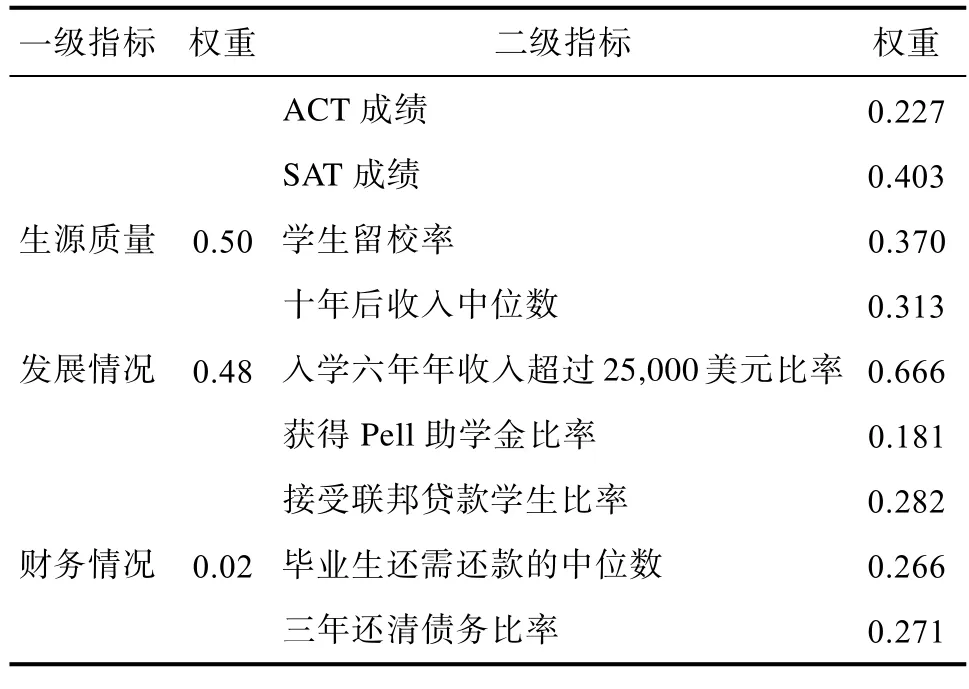
表1　绩效指标权重

2.3绩效指数的计算

绩效值的高低直接反映了一个学校的综合实力及学生的培养质量。据学校的绩效指标选取排名前10的学校,然后用绩效指标乘以学校的人数，并将结果进行归一化处理来确定分配比。分配比乘以获得奖学金总数就是每个学校奖学金的分配金额。结果如下表2：

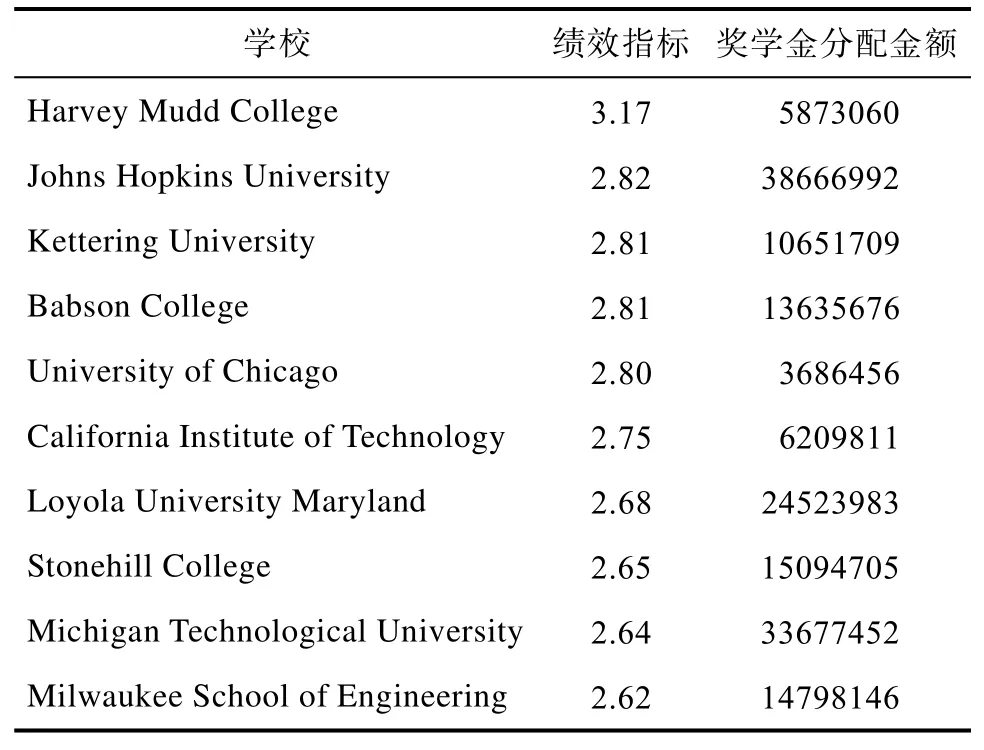
表2　绩效指标

3　结论

本文收集了522所学校的数据，样本很大，并且评价与决策都是基于数据的，结果具有一定的合理性。而且在填补缺失数据方面，采用聚类思想，利用同一类相似性较高的数据来填补并采用客观赋权法的熵值法确定权重，最大限度上的少了误差。

[1] 蒙有华, 徐辉. 美国高等教育捐赠制度探析[J]. 高等教育探索, 2006(6): 41-43.

[2] 王生昌, 付迪, 陈娟娟, 蔡凤田, 张学文. 基于熵值法的汽车动力性能主观评价指标权重确定方法[J]. 路交通科技, 2015, 07: 153-158.

[3] 黄国庆, 王明绪, 王国良. 效能评估中的改进熵值法赋权研究[J]. 计算机工程与应用, 2012, 28: 245-248.

[4] 王化吉, 宗长富, 管欣, 邢如飞, 刘立国. 基于模糊层次分析法的汽车操纵稳定性主观评价指标权重确定方法[J].机械工程学报, 2011, 24: 83-90.

[5] 胡伟. 改进的层次K均值聚类算法[J]. 计算机工程与应用, 2013, 02: 157-159.

[6] 江岸, 黄复刚. 基于熵值法的经济增长质量探析——以甘肃省为例[J]. 财会研究, 2013, 11: 72-75.

Based on the Entropy Method Optimal Allocation Strategy of Goodgrant Fund

JIANG Bao-sheng1, WU Fei1, ZHANG Jing-yi1, GONG Dian-xuan2※
(1. North China University of science and technology, Mathematical modeling innovation laboratory, Tangshan, Hebei, 063000; 2. North China University of science and technology, CollegeofScience, Tangshan, Hebei, 063000)

Goodgrant foundation is a charitable organization in America, It hopes to improve attended universities undergraduate education performance by Charitable donations. In order to use of the funds better, it is necessary to research investment strategy. First of all, all candidate school should be classified by k-means clustering from SPSS. According to the clustering results, these schools are divided into 6 categories. In the same category, filling the missing data by linear in matlab. then classify 13 performance influence factors as the quality of students, the development situation of school and the financial status three first grade indexes. In order to determine objectively the school performance evaluation weight coefficient, Using entropy method to study it. Using Entropy method to calculate the weights of first grade indexes and second grade indexes to make comprehensive evaluation. Use the current performance evaluation standard to calculate each school performance and Ranke all of the schools. Select the top ten schools. Based on the performance of each school performances and the scale of higher education to determine the amount of scholarship allocation.

K-means clustering; Entropy method; Linear; Performance

O29

A

10.3969/j.issn.1003-6970.2016.09.006

国家自然科学基金项目(No.11301120,No.11601151)，河北省自然基金项目(No.A2015209189)，河北省青年拔尖人才支持项目。

通讯联系人: 龚佃选(1981-)，副教授，北京大学访问学者，主要研究方向为计算几何。