基于比例引导法对平行追击问题的研究
曾钰耀
摘 要:文章采用了比例导引法对平行追击问题进行了研究,通过基于比例导引法的导弹平行追击问题模型进行了算法设计。利用MATLAB工具对算法进行编程实现模拟,能够直观有效地看出导弹与目标各自的运动轨迹模型。再根据模拟仿真的结果分析,验证了比例导引法的正确性和有效性。
关键词:平行追击;比例引导法;MATLAB
中图分类号:TP391 文献标识码:A 文章编号:1006-8937(2016)30-0056-04
1 概 述
平行追击问题在运动学当中,属于比较典型的问题。随着科学技术的发展,空战中导弹的使用日益增多。导弹如何采用一种有效合理的攻击方式去攻击目标成为了研究热点。而导弹对攻击目标的打击问题也就是所谓的平行追击问题,本文就是基于此例探讨平行追击问题,通过对导弹追击的连续模型进行离散化,设计算法达到能过MATLAB编程实现模型的地步,对平行追击问题进行研究。
2 引导方法简述
对于导弹平行追击问题来说,选择一种合适的引导方法,就能有效、充分的发挥其性能。通过选择较为合适的引导方法,又或者通过完善现有的引导方法以及去创新一种新的引导方法,这些都是导弹发展环节重要的技术之一。人们在研究导弹的经典引导方法这一问题上得到的结论颇多、贡献较大。常见的有追踪法、平行接近法、比例引导法这三种基本引导方法。
在这三种方法当中,比例引导发是在追踪法与平行接近法这两者方法之间的一种方法。比例引导法,是指导弹在飞行的过程中,导弹的速度矢量的转动角速度和其与追击目标连线的转动的角速度有一定比例的一种引导方法。它能通过自身的参数的调整,来满足对另外两种方法的变化。故与其他两种方法比较起来,比例引导法有较大的优势。本文主要应用比例引导法在导弹平行追击问题的应用进行深层次的研究以及探讨。
3 基于比例引导法的导弹追击问题模型
3.1 模型的基本假设
在导弹平行追击过程中,作如下基本假设:
①不考虑地球曲率以及地球自转影响;
②不计风速等天气状况的影响;
③默认目标物没有较强的机动性;
④认为导弹与追击目标均做匀速运动;
⑤认为导弹有良好的控制系统;
⑥把导弹与追击目标都视于做质点运动。
3.2 导弹与追击目标相对运动模型
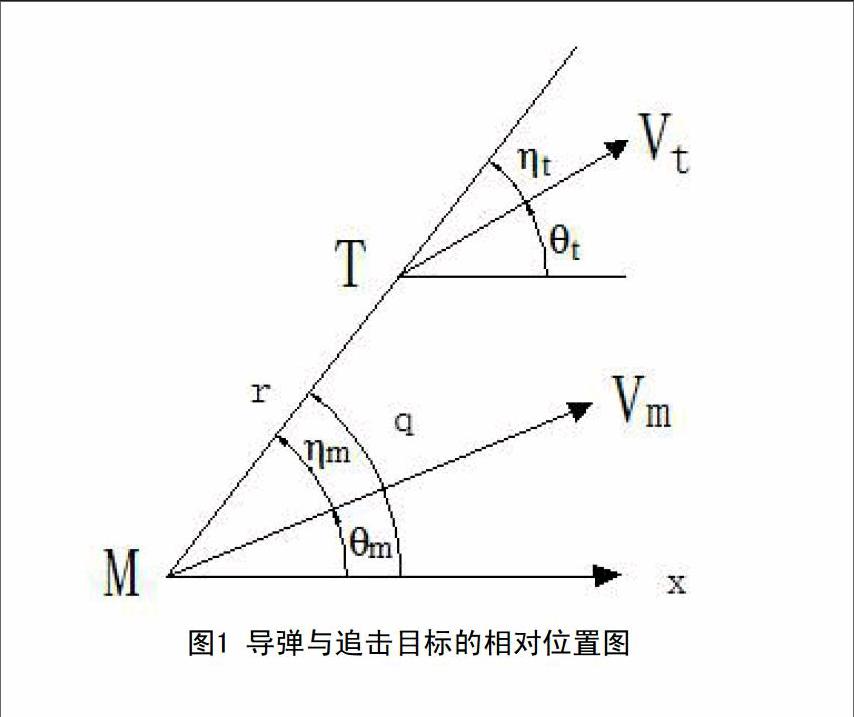
在导弹平行追击问题中,导弹与追击目标的相对运动关系,如图1所示。
比例引导法,是指导弹在飞行的过程中,导弹的速度矢量的转动角速度dθm/dt和目标线的转动的角速度dq/dt有一定的比例的一种引导方法,其中引导关系式为:
导弹M与目标T的相对距离的变化率dr/dt可以表示为导弹速度矢量和目标速度矢量在目标线上分量的代数和;目标线的旋转角速度dq/dr等于导弹和目标的速度矢量分别在垂直面上的矢量代数和再除以它们之间的相对距离r。
综上,导弹与目标相对运动方程:
分析(1)式,我们可以发现导弹击中目标的特性由下面几个因素所决定:
①目标物的特性,比如速度等;
②导弹的特性,比如速度等;
③导弹飞行的时候轨迹的变化规律;
④导弹采用的引导方法,即的选取;
⑤初始时候的取值。
3.3 差分法导弹运动轨迹模型
大多数导弹运动轨迹仿真的文献中,居多数都是只给出了导弹和追击目标在同一平面运动的时候的轨迹的二维图形。本文基于比例导引法的原理,对导弹和追击目标的运动轨迹进行三维的模拟。本文采用差分法,来求得各个时刻的导弹与追击目标各自的离散的三维坐标。通过绘出其坐标点的变化,就能得到模拟的平行追击问题的运动轨迹,同时求出飞行时间、撞击点的坐标。
K-1时刻到k时刻的导弹和追击目标关系,如图2所示。
更改了Δq值后需要将其带入(2)式中再进行迭代差分计算一次,最后得到一系列值。
4 基于MATLAB的导弹追击问题算法实现
4.1 算法设计
根据算法利用MATLAB软件对导弹与目标的运动轨迹模型进行模拟。在实现模拟时,通过采取导弹与目标不同时刻的坐标点进行绘制,用每隔一段时间的三维坐标变化(当导弹与目标之间的距离r等于60时,就判断导弹有效的击中了目标),最终绘制出平行追击问题的一个完整的三维的运动轨迹图。
具体的比例导引法的算法流程图,如图3所示。
4.2 仿真结果
本例采用的初始参数,见表3。
将以上参数带入MATLAB,对应的三维运动轨迹图如图4所示。
经过计算,得到导弹击中目标时导弹运行时间为48.3 s;导弹与目标的最终撞击点A的坐标为(2423.060,9992.971,
25129.392)。
4.2.1 比例导引系数K对导弹轨迹的影响
当采取不同导引系数K值的时候,导弹攻击目标三维运动轨迹图,如图5所示。
从图中我们可以清楚地看到,当K=1的时候,导弹轨迹弯曲是最大的,当K=7时,导弹轨迹弯曲时最小的,基本趋于直线,由此可以得出结论:
当K较小时,导弹运动轨迹越弯曲;K越大时,越接近平行接近法,导弹运动轨迹几乎是平直的,这一点就证明了比例导引法的理论的观点是正确的。
4.2.2 比例导引导弹的速度对导弹轨迹的影响
当设定不同的导弹速度的初始值时,导弹攻击目标三维运动轨迹图,如图6所示。
从图中可以看出,对于不同的导弹初始速度,仿真得到的导弹运动轨迹也有所不同,主要表现在以下方面:导弹初始速度越小,导弹运动轨迹初始段半径越大,轨迹相应就会较为平直;反之,速度比p越大,轨迹初始段曲率半径越小,轨迹就会变得越弯曲;导弹初始越大,相遇距离越近,相遇时间越短;反之,距离越远,时间越长。
4.3 算法优缺点分析
4.3.1 优点
可以得到较为平直的导弹运动轨迹,在与追踪法和平行接近法相比,它没有对发射初始条件有严格的要求,从而能够在技术上得以实施。
4.3.2 缺点
比例导引法还存在明显的缺点,即命中点导弹需用法向过载受导弹速度和攻击方向的影响。为了消除比例导引法的缺点,多年来人们一直致力于比例导引法的改进,研究出了很多形式的比例导引方法。例如,需用法向过载与目标视线旋转角速度成比例的广义比例导引法。
4.4 结果分析
本节根据设计意图绘制出设计流程图,进行比例引导法的算法设计,用MATLAB绘制出导弹与目标的运动轨迹图。
通过以上结果可以清楚地看见导弹与追击目标各自的运动轨迹以及他们之间的运行时间、导弹与追击目标相撞时坐标点的数据情况。这些数据都表明了本次设计初步到达了对平行追击问题的算法设计的要求。
5 结 语
本文通过结合一定的数学知识,通过对平行追击问题的模型进行了连续的离散化,对追击问题进行了经典方式方法的探讨,基于MATLAB软件,对平行追击问题绘制出三维的导弹追击目标模拟运动轨迹图,进一步验证了比例导引法这一导引律的正确性。得出在平行追击问题的关键技术就是对导弹的导引技术。
参考文献:
[1] 姜启源,谢金星,叶俊.数学模型[M].北京:高等教育出版社,2011,01.
[2] 李庆扬,王能超,易大义.数值分析[M].北京:清华大学出版社,2008,12.
[3] 张德丰.MATLAB数值计算方法[M].北京:机械工业出版社,2010.1.
[4] 成叶红.基于Matlab/simulink 的地空导弹制导控制系统动态仿真[J].
战术导弹控制技术,2003,(3):44-48
[5] 张中南,童幼堂,张卫峰.比例导引法导引弹道仿真研究[J].战术导弹技 术,2005(2):56-59
[6] 文仲辉.导弹系统分析与设计[M].北京:北京理工大学出版社,
1989.179-189
[7] 王建成.简明军事科技发展史[M].北京:国防工业出版社,2005.2-33
[8] 谷良贤,温炳坤.导弹总体设计原理[M].西安:西北工业大学出版社,
2004.73-75
[9] 孟秀云.导弹制导与控制原理[M].北京:北京理工大学出版社,2004.
[10] 黄德庆.防空导弹控制与制导[M].西安:陕西人民教育出版社,1989.
[11] 李忠应.空空导弹全向攻击最优制导规律研究[J].北京航空航天大学
学报,1990,16(10):110-116.
[12] 胡建和,李忠应.地-空导弹自适应最优制导律初探[J].北京航空航天 大学学报,1991,17(3):101-110
[13] George Voulgaris. Book Reviews: A Guide to MATLAB for Beginn
ers and Experienced Users by Brian R. Hunt, Ronald L. Lipsman,
and Jonathan M. Rosenberg with Kevin R. Coombes, John E.
Osborn, and Garret J. Stuck. Data Analysis in the Earth Sciences
Using MATLAB by Gerard V. Middleton[J]. Mathematical Geology,
2004,360-364.
[14] Denis Talay. Model Risk in Finance: Some Modeling and Numeric
al Analysis Issues[J].Handbook of Numerical Analysis,2009,15.25
-30.
[15] Bezick S.Guidance of a homing missile via nonlineear geometric
control method[J]..Control and Dynamics,1995,18(3):441-448.

