基于条件数理论的高维组合导航系统可观测性分析

石静+杨建华+曹晓欢+迪玉茹

摘要： 为了更好地完善惯导系统误差补偿和抑制技术， 对SINS/GPS组合导航系统进行可观测性分析， 从而对系统误差进行补偿， 提高导航精度。 利用分段线性定常理论得到系统的提取可观测性矩阵， 再计算该矩阵的条件数， 根据条件数分析在不同量测及不同机动方式下系统的可观测性。 针对SINS/GPS组合导航系统， 建立高维数学模型， 设置复杂运动轨迹， 比较不同量测下误差源的可观测性。 仿真结果表明：与机动方式的激励作用相比， 增加量测能更有效地提高系统的可观测性。

关键词： 捷联惯性导航系统； 全球定位导航系统； 组合导航； 分段线性定常理论； 条件数； 可观测性分析

中图分类号： TJ765；TN967.2文献标识码： A文章编号： 1673-5048（2016）04-0025-05

Abstract： In order to improve the error compensation and suppression technology of inertial navigation system， the observability analysis is carried out on the high precision SINS/GPS integrated navigation system， so as to compensate the system error and improve its navigation accuracy. The extraction observability matrix is obtained by the theory of piecewise linear constant system， and the condition number of this matrix is calculated to analyzing the observability of the system errors under different measurements and maneuver mode. For the SINS/GPS integrated navigation system， high dimension model is established， complex trajectory is set， and different measurement equations are chosen to compare the observability. Simulation results show that adding velocity measurement can obviously improve the observability， and this effect is better than the excitation of maneuver mode.

Key words： strapdown inertial navigation system； global positioning system； integrated navigation； piecewise linear constant system； conditioning number； observability analysis

0引言

国外先进的惯导产品采用了一系列误差补偿和抑制技术， 而国内相关技术研究起步较晚， 与国外存在较大差距。 对系统进行可观测性分析， 确定最优激励方法[1-2]， 从而提高系统可观测性， 完善惯导系统误差补偿技术。

捷联惯导中存在的各种误差源是影响导航精度的主要因素[3-4]。 类似惯导解算误差、 器件误差、 安装误差等如果得不到有效补偿， 由此引起的等效漂移或零偏将会持续增大， 必将导致系统导航精度降低。 如果能够对各种误差源的可观测性做出准确分析， 获取误差模型的关键参数， 对系统实时地加以动态补偿， 则可以有效提高导航精度[5]。 然而， 对于高维数系统， 目前还没有有效的可观测性分析方法。

对于时变系统， 通常使用分段线性定常系统理论（Piece-Wise Constant System， PWCS）得到系统的可观测性矩阵来分析误差状态的可观测性[6-7]，并通过计算该可观测性矩阵的特征值或奇异值来分析误差状态的可观测度[8]。 当可观测性随时间变化时， 需要计算从0时刻到当前时刻矩阵的秩， 此计算量非常大， 对于高维系统更是如此。 鉴于此， 为简化计算量使用提取可观测性矩阵， 并通过计算该矩阵的条件数来分析系统的可观测性[9]。

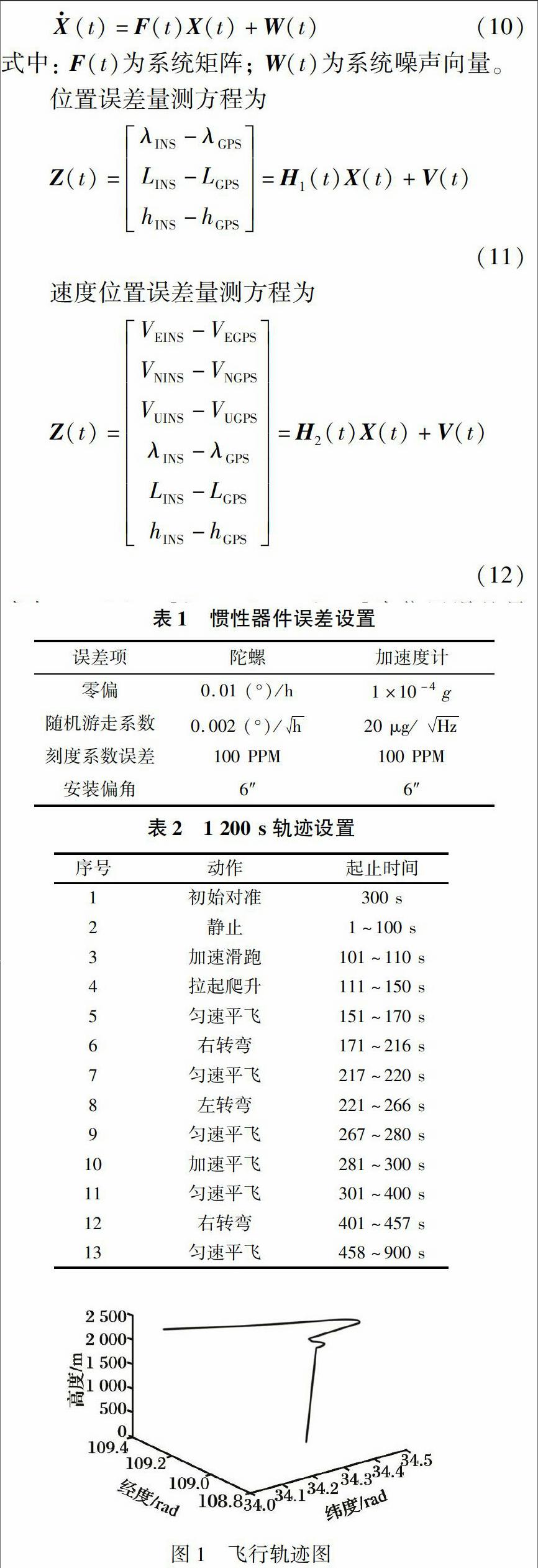
针对SINS/GPS组合导航系统， 建立高维数学模型， 选择不同量测并设置复杂运动轨迹， 分析该系统的可观测性。

1基于条件数的可观测性分析方法

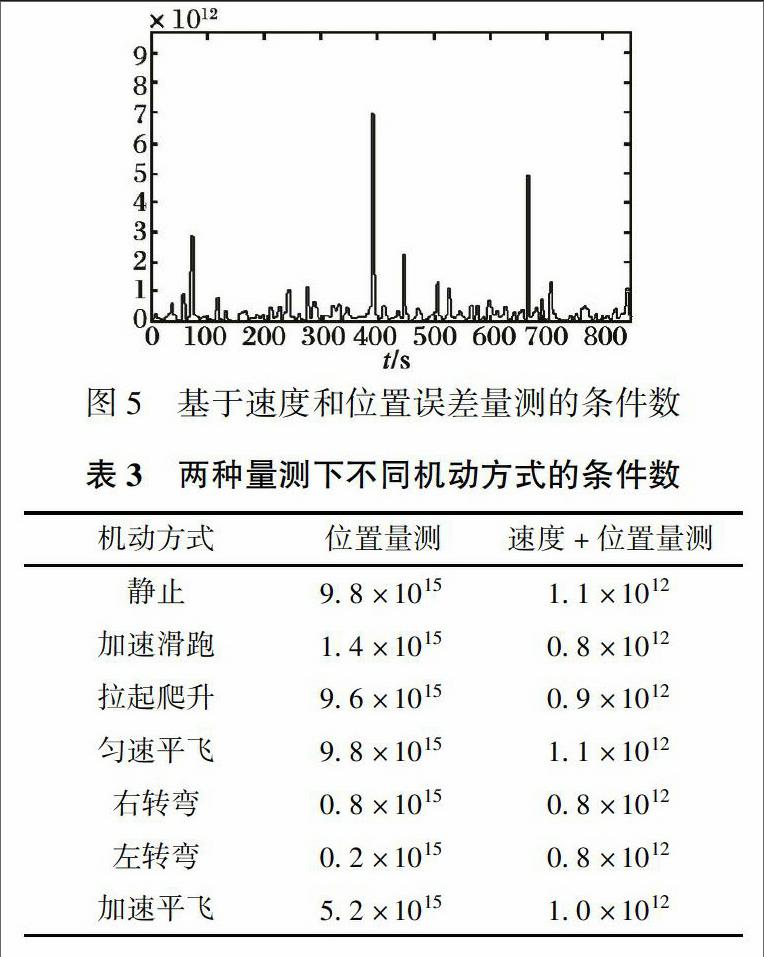
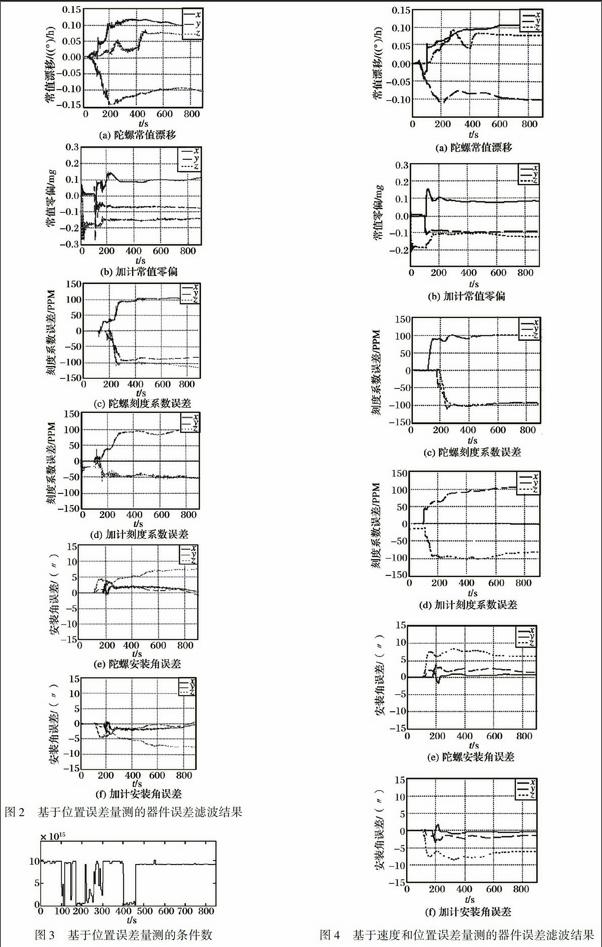
基于位置误差量测的Kalman滤波结果见图2， 该量测下的条件数见图3。 基于速度和位置误差量测的Kalman滤波结果见图4， 该量测下的条件数见图5。 另外， 在两种量测下不同机动方式的条件数见表3。

对比图2和图4可以发现， 基于速度位置误差量测的方法对器件误差的整体估计效果更好。 从图3可以看到， 基于位置误差量测的条件数整体位于一个较高的水平（数量级为1015）， 而在加速和转弯这两种机动状态下， 条件数有所下降， 结合表3可知， 加速滑跑、 右转弯、 左转弯阶段的条件数分别为1.4×1015， 0.8×1015和0.2×1015， 明显小于其他机动状态下的条件数， 可见， 这三种运动方式能够提高系统的可观测性。 从图5可以看到， 基于速度位置误差量测的条件数整体位于一个较低的水平（数量级为1012）， 说明增加了速度误差量测后有效提高了系统的可观测性， 但在这种情况下， 机动方式对误差可观测性的激励作用不明显， 表3中给出的不同机动方式下条件数的具体数值也说明了这点， 可见， 增加量测对改善系统可观测性的作用更大。

4结论

本文针对SINS/GPS组合导航系统， 建立高维数学模型， 应用分段线性定常系统理论得到系统的提取可观测性矩阵， 然后计算该矩阵的条件数， 根据条件数并结合滤波结果分析系统在不同量测及不同机动方式下的可观测性。 仿真结果表明：增加速度量测能有效提高系统可观测性， 并且与机动方式的激励作用相比效果更好。

参考文献：

[1] 吴晓. 长航时高精度捷联惯导系统误差抑制技术研究[D]. 啥尔滨： 哈尔滨工程大学， 2012.

[2] 高贤志， 王丹. 单轴旋转式惯导系统误差抑制机理分析[J]. 舰船科学技术， 2012， 34（8）： 67-72.

[3] 王新龙， 谢佳， 王君帅. SINS/GPS不同组合模式适应性分析与验证[J]. 航空兵器， 2013（3）： 3-8.

[4] 孙兆妍， 王新龙， 车欢. GPS/SINS深组合导航技术综述[J]. 航空兵器， 2014（6）： 14-19.

[5] 杨晓霞， 阴玉梅. 可观测度的探讨及其在捷联惯导系统可观测性分析中的应用[J]. 中国惯性技术学报， 2012， 20（4）： 405-409.

[6] GoshenMeskin D， BarItzhack I. Observability Analysis of PieceWise Constant systems. I. Theory[J]. IEEE Transactions on Aerospace and Electronic System， 1992， 28（4）： 1056-1075.

[7] 孔星炜， 董景新， 吉庆昌， 等. 一种基于 PWCS 的惯导系统可观测度分析方法[J]. 中国惯性技术学报， 2012， 19（6）： 631-636.

[8] Ma Yanhong， Hu Jun. Counterexamples for Degree of Observability Analysis Method Based on SVD Theory[J]. Journal of Chinese Inertial Technology， 2008（4）： 19.

[9] 刘准， 陈哲. 条件数在系统可观测性分析中的应用研究[J]. 系统仿真学报， 2004， 16（7）： 1552-1555.

[10] 秦永元， 张洪钺， 汪叔华. 卡尔曼滤波与组合导航原理[M]. 西安： 西北工业大学出版社， 1998.

[11] Cao Jingyu， Tang Jianjun， Wang Yu， et al. Observability Analysis of FourPosition Alignment for Laser Gyroscope StrapDown Inertial Navigation System[C]∥2011 International Conference on Electronics and Optoelectronics （ICEOE）， 2011： 227-230.