小波分解层数对电离层预报的影响

周淼，方辉

(桂林市测绘研究院，广西 桂林 541002)



小波分解层数对电离层预报的影响

周淼*，方辉

(桂林市测绘研究院，广西 桂林 541002)

针对电离层总电子含量(TEC)所具有的非线性、非平稳的特性，本文将小波分析理论引入到时间序列分析方法中，对IGS中心提供的不同纬度前8 d电离层格网点观测数据进行不同层数的分解，而后采用ARIMA模型预报后4d TEC数据。将预报结果与观测数据对比并统计精度，实验结果表明对电离层格网点数据进行1层～3层分解能够取得较好的预报效果，并且采用1层分解所得预报效果最佳。

电离层；小波分解；ARIMA；TEC；时间序列

1 引 言

自美国于2000年取消SA政策之后，电离层延迟误差就成为GNSS的主要误差来源，在极端情况下误差甚至可达 100 m[1]。电离层总电子含量(Total Electronic Content，TEC)是表征电离层特性的一个重要参量，如何对其进行预报已经成为国内外学者研究的热门课题。原有的Klobuchar模型[2]、IRI模型[3]等经典模型虽然具有计算简便、应用广泛等优点，但存在对电离层整体改正率不高的缺陷。为此，有些学者采用一定的方法对其进行改进，但依旧存在对夜间改正率无法提高，使用范围比较有限等缺点[4～6]。另一方面，国内外学者根据GNSS对电离层的实测数据，采用神经网络[7，8]、时间序列[9～11]、集合卡尔曼滤波[12]等方法进行预报，取得了较好的预报效果，但仍存在网络优化复杂，参数选取困难，研究范围单一等缺陷。

自回归移动平均模型(ARIMA)是对时间序列进行分析的一种常用方法，通过差分能将非平稳时间序列转变为平稳时间序列，是对非平稳时间序列的数据进行平稳化处理并预报的一种常用方法。另一方面，小波分析(Wavelet Analysis)是近年来发展起来的一种时频分析方法，其对信号具有良好的局部化性质，能够提取信号的任何细节等特性，为非平稳时间序列数据的预处理提供了一种新方法[13]。目前，已有研究表明，将小波分析与ARIMA模型相结合对电离层TEC数据进行预报能取得较好的预报效果，但对数据分解层数的选择存在问题，有待进一步解决[14]。基于此，本文将采用IGS中心提供的电离层格网点TEC的前 8 d观测数据进行不同层数的小波分解，对分解数据采用ARIMA模型对未来 4 d的TEC值进行预报，并对预报值进行精度评定。

2 模型简介

2.1 ARIMA简介

ARIMA(p ，d，q)×(P，D，Q)因其具有计算简单、操作方便的特点，成为非平稳时间序列预报的一种常用方法。其中，非负整数p为自回归阶数；非负整数d为d阶常规差分；非负整数q为滑动平均阶数；非负整数P为季节性自回归阶数；非负整数D为D阶常规差分；非负整数Q为季节性滑动平均阶数。建模预报前，根据非平稳时间序列表现的周期性，选取相应的差分类型对其进行差分。关于ARIMA的详细内容可参考文献[10]。

2.2 小波分析基本理论

根据小波分析理论可知，小波分解具有良好的局部化特性，能够聚焦到信号的任意细节。根据小波分解的层数，可将原始序列分解成一个概貌序列和与分解层数相同个数的细节序列，且分解得到的序列具有更好的平稳性和平滑性。因此，对于一些非平稳时间序列，经过小波分解后便可以使用传统的时间序列方法建模预报。关于小波分解的详细内容可参考文献[13]。

2.3 模型建立

(1)利用db4正交小波对IGS中心提供的前8天TEC序列分别进行分解层数为1层～5层的小波分解，得到概貌序列和细节序列。

(2)分别判断概貌序列和细节序列的平稳性。如为非平稳序列，则需要根据表现出来的特性选用相应性质的差分类型对其进行差分。

(3)根据差分所得序列的自相关图和偏相关图所表现出来的特性，确定p(P)、q(Q)的取值。

(4)根据p(P)、q(Q)的取值对模型进行相关性检验及不断尝试，选择使SBC函数取得最小值的模型预报值分别作为概貌序列和细节序列的预报值。

(5)对预报值进行小波重构，得到最终预报序列。

3 实验分析

3.1 实验数据

本文选取IGS站提供的2013年年积日为072-083的高纬度(75°N、125°E)、中纬度(45°N、125°E)、低纬度(15°N、125°E)TEC值作为实验数据。对前 8 d数据，分别进行1层～5层分解，而后对分解数据建立ARIMA模型。并选取均方根误差RMSE和相对精度P对预报数据进行精度评定，其计算公式如下：

(1)

(2)

式中，Ipre[i]表示预报结果；Iigs[i]表示IGS站提供的TEC观测值；n表示预报天数的第n天；RMSE表示预报结果与IGS站提供的TEC观测值误差的日平均均方根误差；P表示预报结果的日平均相对精度。

3.2 实验结果

利用db4小波对前8 d观测数据分别进行分解层数为1层～5层的小波分解，并对分解所得数据采用ARIMA模型进行4 d预报，所得预报结果与实际观测数据的对比如图1所示。图中，横坐标轴表示时间，单位为h，其中每 2 h为一个历元；纵坐标轴表示TEC值，单位为TECu；黑色表示IGS中心提供的观测值；红色、蓝色、绿色、紫色、粉色分别表示对观测数据进行1层～5层分解所得的预报值。从图中可以看出，对三个纬度区域的IGS观测数据采用小波分解与ARIMA模型对其进行预报，大多数情况下均能较好的反映电离层变化特性。其中，对观测数据进行1层～3层分解所得预报效果较对其进行4层～5层所得预报效果更好。并且，在中纬度地区和低纬度地区，对观测数据进行1层～3层分解所得预报效果大致相同。

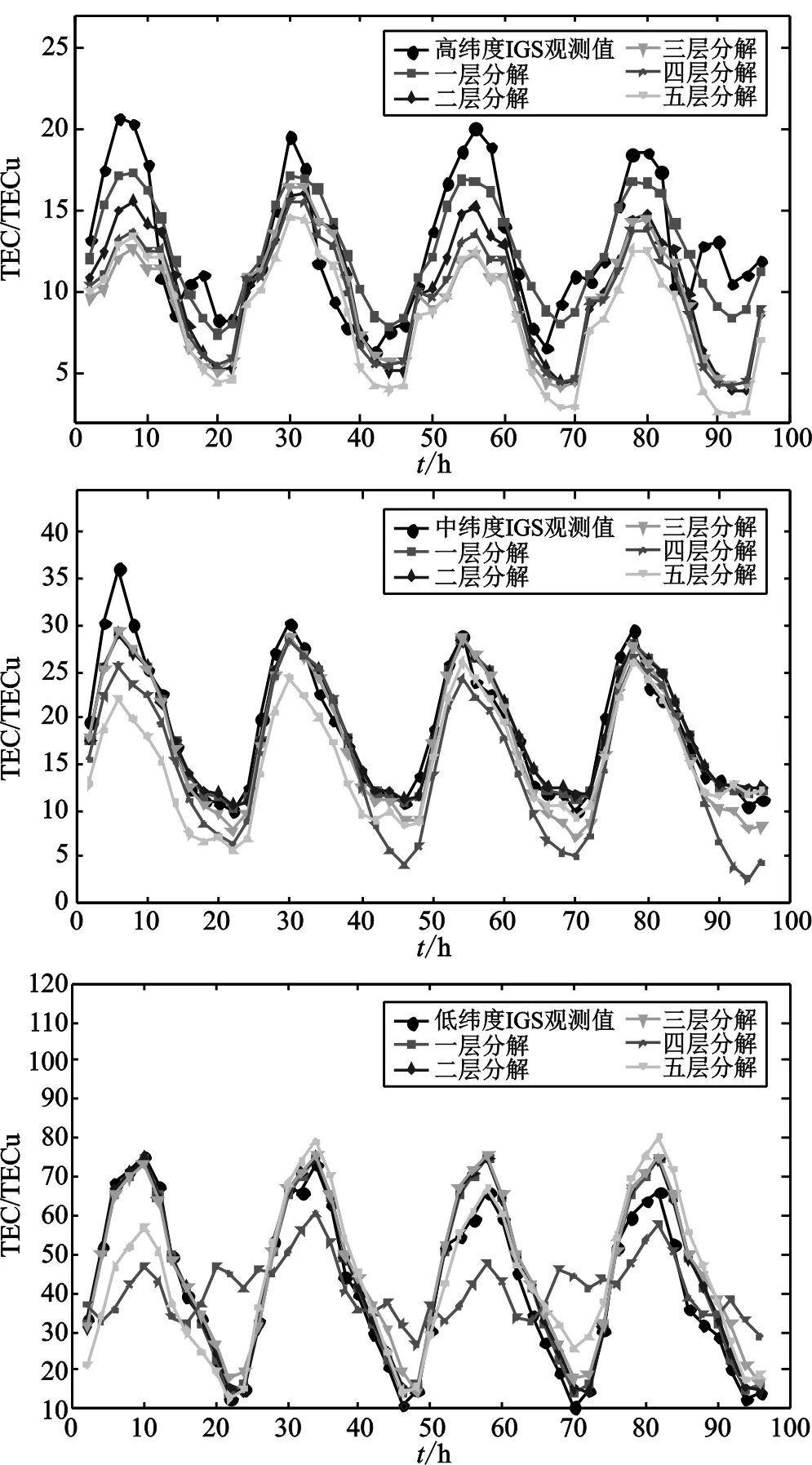
图1 不同纬度不同分解尺度预报对比图

为了说明对观测数据进行不同分解层数预报所能达到的预报效果，将预报所得结果与IGS中心提供的观测数据进行对比，统计其日平均均方根误差与日平均相对精度，其结果可如表1所示。

从表1中可以看出，对观测数据采用相同分解层数进行预报，对预报所得的日平均均方根误差，在中纬度地区最小，其次为高纬度地区，最后是低纬度地区；比较预报所得日平均相对精度可以发现，中纬度地区最高，其次是低纬度地区，最后是高纬度地区。造成这种情况的主要原因可能是：中纬度地区电离层变化规律相对简单、稳定，不存在异常性突变，因此便于预报；对低纬度地区，虽然预报具有较高的相对精度，但是由于其TEC值的基数比较大，使得其日平均均方根较大；对高纬度地区，由于受太阳直射影响较小，TEC值也较小，导致预报所得相对精度和均方根误差均介于中纬度地区和高纬度地区之间。

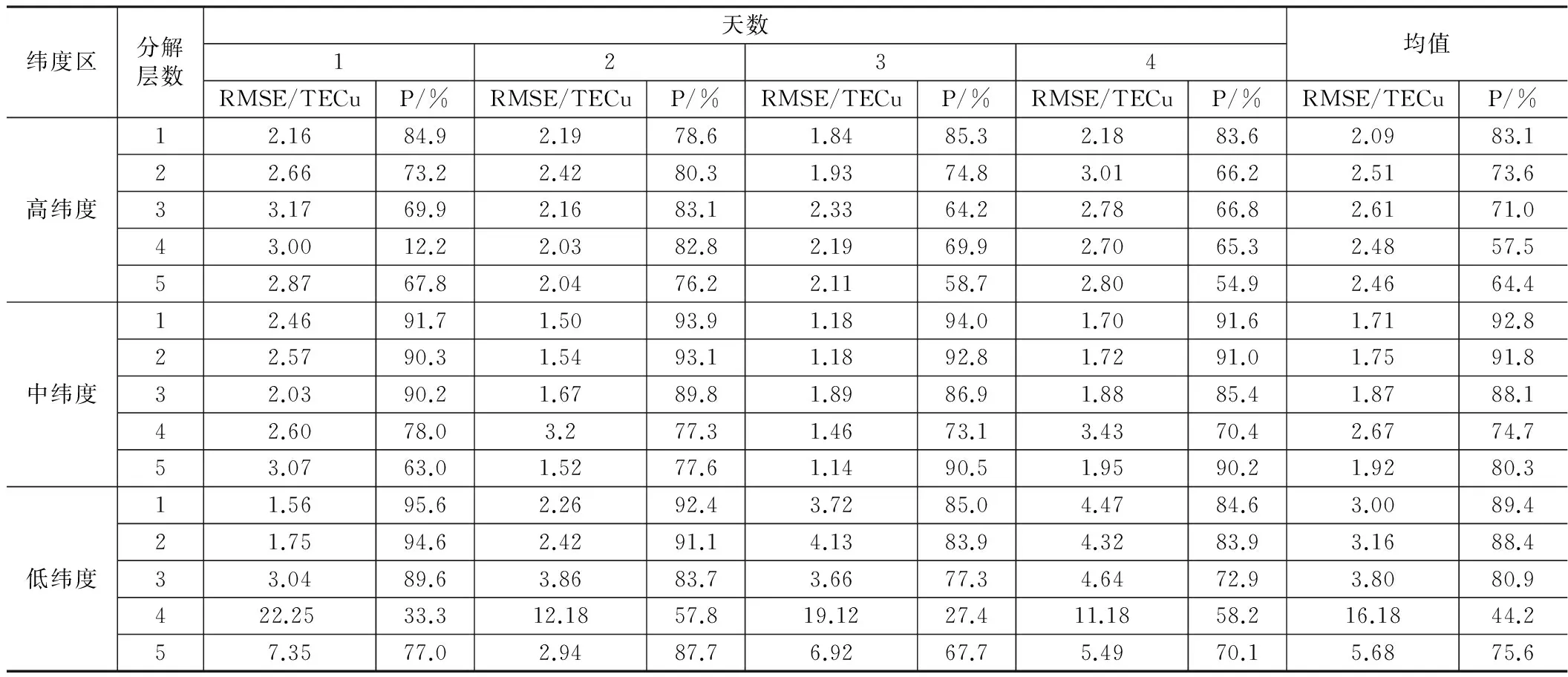
不同分解层数预报精度统计 表1

对同一纬度区的观测数据，进行不同层数的分解所得预报结果均具有类似的变化规律：1层分解预报效果最好，其次是2层分解，3层分解，5层分解，最后是4层分解。这一变化规律在低纬度地区表现特别明显，在高纬度地区则没有那么明显的变化规律。其中，采用1层～3层分解所得预报结果效果较好。但是当采用4层分解进行预报的时候，预报效果锐减，而5层分解所得预报结果有所回升。造成这一变化规律的主要原因可能是：由于小波重构是对小波分解所得系数进行重构，在预报中也是对分解所得系数进行预报，因此，在重构过程中将产生重构误差。同时，对所采用的TEC数据，重构误差将随着分解层数的增加而增加，并在在4层分解进行重构的时候，所产成的重构误差达到最大，因此4层分解效果最差；当对TEC5层分解数据进行重构时，误差减小，因此5层分解预测效果优于4层分解。

4 结 论

本文分别对IGS中心提供的前8 d电离层观测数据，采用1层～5层的小波分解，并对分解所得数据采用ARIMA模型进行4 d建模预报，通过将预报所得数据与所提供的观测数据进行对比分析后其结论如下：

(1)采用1层～5层小波分解对观测数据进行分解预报，所得预报结果均能够较好地反应电离层变化特性。

(2)对观测数据采用1层～3层小波分解预报，能够获得较好的预报效果。其中，进行一层分解所得预报效果最佳。

致谢：

感谢IGS中心提供的电离层格网点数据。

[1] 张强，赵齐乐，章红平等. 北斗卫星导航系统Klobuchar模型精度评估[J]. 武汉大学学报·信息科学版，2014(2)：142～146.

[2] Klobuchar J A. Ionospheric time delay algorithm for single frequency GPS Users[J]. IEEE Trans. Aerospace Elec. Syst.，1987，23(3)：325～331.

[3] 方涵先，翁利斌，杨升高. IRI、NeQuick和Klobuchar模式比较研究[J]. 地球物理学进展，2012(1)：1～7.

[4] 蔡成辉，刘立龙，黎峻宇等. 基于改进的Klobuchar模型建立南宁市区域电离层延迟模型[J]. 大地测量与地球动力学，2015(5)：797～800.

[5] 蔡成辉，刘立龙，黎峻宇等. 基于附有限制条件的多项式模型建立中国区域电离层模型[J]. 大地测量与地球动力学，2015(6)：1007～1011.

[6] 章红平，平劲松，朱文耀等. 电离层延迟改正模型综述[J]. 天文学进展，2006(1)：16～26.

[7] 范国清，王威，郗晓宁. 基于广义回归神经网络的电离层VTEC建模[J]. 测绘学报，2010(1)：16～21.

[8] 翁利斌，方涵先，缪子青等. 利用人工神经网络提前1h预报电离层TEC[J]. 空间科学学报，2012(2)：204～208.

[9] 陈鹏，姚宜斌，吴寒. 利用时间序列分析预报电离层TEC[J]. 武汉大学学报.信息科学版，2011(3)：267～270.

[10] 张小红，任晓东，吴风波等. 自回归移动平均模型的电离层总电子含量短期预报[J]. 测绘学报，2014(2)：118～124.[11] 汤俊，姚宜斌，陈鹏等. 利用EMD方法改进电离层TEC预报模型[J]. 武汉大学学报.信息科学版，2013(4)：408～411.

[12] 陈春，吴振森，孙树计等. 集合卡尔曼滤波在电离层短期预报中的应用[J]. 空间科学学报，2010(2)：148～153.

[13] 徐科，徐金梧，班晓娟. 基于小波分解的某些非平稳时间序列预报方法[J] . 电子学报，2001(4)：566～568.

[14] 鲍亚东，刘长建，柴洪洲. 小波分解改进电离层VTEC时间序列预报模型[J]. 大地测量与地球动力学，2015(5)：784～787.

Wavelet Decomposition Level Impact on Ionospheric Prediction

Zhou Miao，Fang Hui

(Guilin Surveying and Mapping Research Institute，Guilin 541002，China)

This paper brings wavelet analysis theory into time series analysis method aiming at the nonlinear and non-stationary characteristic of Total Electronic Content in ionosphere. We decomposed the former 8 days’ ionospheric grid observe TEC data in different latitude provided by IGS center in different layer，then forecast the latter 4 days’ TEC data with ARIMA model. Then we compare the forecast result with observe data and get the statistical accuracy，the result shows that we can achieve a rather good prediction effect decomposed in 1～3 layers. Also，we can get the best forecast result just decomposed in 1 layer.

ionosphere；wavelet decomposition；ARIMA；TEC；time series

1672-8262(2016)05-99-04

P228

A

2016—06—05

周淼(1988—)，男，硕士，助理工程师，研究方向GNSS气象学。

国家自然科学基金项目(41541032，41664002)；广西空间信息与测绘重点实验室项目(15-140-07-29)；广西“八桂学者”岗位专项经费项目；广西高校中青年教师基础能力提升项目(KY2016YB189)。