基于中心差分卡尔曼滤波的初始对准方法研究

贾鹤鸣，杨泽文，宋文龙

(东北林业大学 机电工程学院，哈尔滨 150040)



基于中心差分卡尔曼滤波的初始对准方法研究

贾鹤鸣，杨泽文，宋文龙*

(东北林业大学 机电工程学院，哈尔滨 150040)

由于建立的大方位失准角下的捷联惯性导航系统误差模型具有非线性的特点，本文选用中心差分卡尔曼滤波(CDKF)方法对捷联惯导系统的控制对象进行初始对准仿真。并与无迹卡尔曼滤波(UKF)和扩展卡尔曼滤波(EKF)两种滤波方式进行比较，最后得出CDKF可以提高系统的图像和目标的滤波精度的结论，并且不需要具体模型计算出解析方程，节约了计算复杂的具有驱动约束方程的雅可比(Jacobian)矩阵的时间。最后的仿真结果证明CDKF对系统状态进行最优估计的算法明显优于EKF和UKF，同时具有较高的精度和收敛性，能够满足在非线性模型下的系统对导航的要求。

大方位失准角；捷联惯导；初始对准；CDKF

0 引 言

SINS(捷联惯性导航系统)中所不可或缺的一项技术是初始对准，在初始对准过程中的控制精度和所用时间会影响到整个系统的工作静态和动态性能[1-5]。扩展卡尔曼滤波(EKF)方法在失准角误差模型的非线性系统应用很多[6-7]，然而这种滤波方法存在精确度和准确性的缺点，例如在将非线性方程问题变成线性方程问题来的求解过程中，通常会忽略泰勒级数展开式中部分的高阶项，因此造成EKF滤波方式出现了较大的线性化误差，从而降低滤波精度甚至会使结果发散，造成工作状态难以稳定，并且推导具有驱动约束方程的雅可比(Jacobian)矩阵需要的时间长，因此在实际中很难广泛应用。

针对EKF的不足，近年来人们提出了Sigma点卡尔曼滤波(SPKF)方法，其分析系统的性能较EKF比有较大的改善。SPKF主要分为两种，一种是中心差分卡尔曼滤波(CDKF)，另一种是无迹卡尔曼滤波(UKF)。 CDKF 最早由ITO[8]和Norgaard[9]等人提出，他们基于卡尔曼在NASA埃姆斯研究中心时产生灵感发现的滤波方法，使CDKF避开了EKF滤波时需要被控系统模型计算出具体解析方程的劣势，并能隔离随机变量噪声，具有较低的线性化误差和高定位准确度的优点。另外，CDKF比 UKF的理论精度高。因此CDKF方法在目前导航、航空领域中有诸多的应用，效果也十分完善。

本文首先介绍了中心差分卡尔曼滤波的原理，然后从基于欧拉平台误差角描述实际地理坐标系再到分析其与计算地理坐标系的变换关系，最后创建一个SINS在失准角为大方位条件下的非线性模型；研究CDKF在SINS大方位失准角初始对准条件下滤波效果。本文分别利用了EKF、UKF和CDKF三种方法进行了仿真验证并进行比较，仿真结果进一步证明了中心差分卡尔曼滤波(CDKF)方法显著优于EKF和UKF。是一种更为优越，实用性强的非线性滤波方法。

1 SINS大方位失准角初始对准误差模型

上者的转移关系可用以下列矩阵来表示：

(1)

(2)

(3)

(4)

当φx，φy很小时cosφx=cosφy=1，sinφx≈φx，sinφy≈φy，则

(5)

(6)

1.1 速度误差方程

理论上，SINS的速度微分方程表示为：

(7)

不忽略外界干扰情况下，SINS的速度微分方程为：

(8)

(9)

1.2 姿态角误差方程

(10)

(11)

失准角运动方程为：

(12)

(13)

(14)

(15)

1.3 建立非线性捷联惯性导航系统初始对准模型

假设计算出的陀螺仪的误差漂移εb是一个恒定值；加速度计的误差是恒定值零偏b；假定在静基座快速初始对准条件下，所在位置是恒定不变的且已知的，此刻满足=[0 ωiecosL ωiesinL]Tvt=0；其中R为地球半径，L为纬度，忽略重力误差项δgt以及不考虑δvz，则可得状态方程为：

(16)

令状态向量X为：

用捷联惯性导航系统两程度速度误差X=δVt作为观测误差并测量，建立非线性对准模型：

(17)

其中，f(X)的表达式可以参考公式(16)进行表示，G是10×5维的矩阵系数，G(1,1)=G(2,2)=G(3,3)=G(4,4)=G(5,5)=1，H代表量测矩阵H=[02×3∶I2×2∶02×5]，V代表量测噪声。

2 基于CDKF的状态估计

2.1 中心差分变换 中心差分变换是研究在SINS在失准角为大方位条件下中心差分卡尔曼滤波滤波器的基础，同时它也是一种以插值理论为基础的高效的非线性变换方法，是SPKF的一种，可以用来求解经过非线性变换后的一些统计学量，例如均值和方差。研究CDKF的切入点是借助sterling差值定理，进而求取逼近多项式非线性方程的导数，节约了进行复杂求导运算的时间，它运用了中心差分方法代替泰勒展开式中指数为1和2[10]。

y=f(x)。

(18)

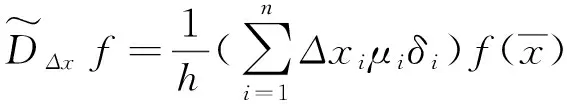
(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

其中Sxi表示柯勒斯基(cholesky)分解中Sx的第i列。

2.2 中心差分卡尔曼滤波方法研究

CDKF虽然表达形式与EKF类似，实际上却是利用先验分布构造一组确定性采样点 Sigma 点，充分考虑了高斯随机变量的统计特性[13-14]，并用经过线性回归变换后得到的Sigma(一组确定性采样点)来表示实验状态的后验分布。针对非线性滤波的难题[15-16]CDKF 采用了中心差分变换方法，并且发现CDKF较传统EKF算法具有滤波精度高，过程较稳定的优点，且不需要计算具有约束方程的Jacobian；节约了大量的时间，而与UKF滤波算法相比较，其又具有精度高，对状态协方差敏感性要低的优点。同时，在CDKF中，当出现系统测量噪声和系统本身自有噪声均为复杂加性噪声的情况时，为了减轻滤波计算，可不进行状态增广。由此可见，CDKF与上面两种滤波算法相比而言，在处理SINS大方位失准角初态对准方面问题中具有相当明显的优势。

设非线性系统为：

(28)

其中，k时刻的状态向量为xk，观察向量用yk，wk和vk为两两互不关联的均值为0的高斯噪声。针对上述非线性模型，利用中心差分变换方法进行状态估计，推导出中心差分卡尔曼滤波的算法[17]如下：

(1)初始化

(29)

(30)

(2)确定权值

(31)

(32)

(3)确定sigma点集

(33)

(4)时间更新

(34)

(35)

(36)

(5)sigma点更新

(37)

(6)量测更新

yk/k-1=h(χk/k-1)。

(38)

(39)

(40)

(41)

(42)

(43)

(44)

3 仿真研究

3.1 仿真条件

在静基座初始对准状态下，假定当前的初态失准角度φx=φy=0.6°，φz=10°；陀螺仪常值漂移为0.02°/h；随机漂移为0.01°/h；加速度计零偏为100 μg；随机偏差为50 μg；速度测量误差为0.1 m/s；当地地理纬度为45.779 6°，则P(0)、Q、R可表示为：

P(0)=diag{(0.6°)2,(0.6°)2,(10°)2,(0.1 m/s)2,(0.1 m/s)2,(0.02°/h)2,(0.02°/h)2,(0.02°/h)2,(100 μg)2,(100 μg)2}

Q=diag{(0.01°/h)2,(0.01°/h)2,(0.01°/h)2,(50 μg)2,(50 μg)2,0,0,0,0,0}

R=diag{(0.1 m/s)2,(0.1 m/s)2}。

得到上述仿真条件，分别采用扩展卡尔曼滤波器(EKF)、无损卡尔曼滤波(UKF)和中心差分卡尔曼滤波(CDKF)三种方法对系统进行滤波仿真比较，仿真时间均设定为300 s。

3.2 仿真结果分析

失准角估计误差的对比情况见表1。系统的仿真结果如图1和图2所示。

表1 大方位失准角的估计误差Tab.1 Estimation error of large azimuth misalignment

因为北向和东向的水平失准角仿真估计结果类似，所以图中只列出了系统中北向估计的结果。从北向水平失准角的曲线图和大方位失准角的误差表很容易得出，每个滤波算法对在两方向失准角条件下的仿真结论基本相当，收敛速度都很快，均能得到很好很稳定的滤波结果。从图2和表1得出，UKF和CDKF两者对大方位失准角的估计，收敛速度、时变系统跟踪速度与收敛精度优于EKF，首要原因是 EKF在线性化滤波过程中存在一阶截断问题，会产生截断误差，造成方位失准角误差的急剧增大，而UKF因为算法中存在二阶截断问题，会使方位失准角误差增加的更快，所以效果也不如CDKF。CDKF与UKF相比，CDKF具有在相同增长时，接近稳定值的速度较快和滤波精度高的特点。因此CDKF在三种滤波方式中拥有相当显著实用的优点。

图1 北向水平失准角的误差曲线Fig.1 Estimation error curves of north misalignment

图2 天向失准角预计的误差曲线Fig.2 Estimation error curves of azimuth misalignment

4 结 论

本文内容深入研究CDKF滤波，并在SINS大方位失准角初始对准中得到了广泛的应用，利用其具有精度高，稳定性好的优点，有效解决了复杂的误差模型具有的非线性问题。以上仿真出的图形和表格表现出CDKF比EKF具有更高滤波精度，同时节约了求解复杂的雅可比矩阵的时间，提高了系统可靠性，这些优点都将是CDKF成为更主流滤波方法的重要因素。CDKF与UKF相比，CDKF不但具有滤波精度高和保证收敛速度比较快的特点，同时减少了工作量，使数值的稳定程度提高。仿真结果证实了CDKF的确在基于中心差分卡尔曼滤波对大方位失准角初始对准问题中较其他仿真方法而言优越性非常的显著，实现功能更加容易便捷，实际应用愈加广泛，是一种研究非线性系统滤波十分高效的算法。

[1]Ito K，Xiong K.Gaussian filters for nonlinear filtering problems[J].IEEE Transactions on Automatic Control，2000,45(5)：910-927.

[2]NØrgaard M，Poulsen N K，Ravn O.Advances in derivative-free state estimation for nonlinear systems[R].Informatics and Mathematical Modelling，Technical University of Denmark，DTU，1998.

[3]刘国海，李康吉.基于PDA的GPS定位精度提高方法[J].江苏大学学报：自然科学版.2005，26(5)：448-452.

[4]Norgaard M，Pouisen N K，Ravn O.New Developments in State Estimation for Nonlinear System[J]．Automatica，2000，36(11)：1627-1638.

[5]Van Der Merwe R.Sigma-point Kalman filters for probabilistic inference in dynamic state-space models[D].Oreg：Oregon Health & Science University，2004.

[6]王海勃，陈红林，韩惠珍.CDKF在GPS/SINS组合导航系统非线性模型中的应用[J].现在电子技术，2011，34(11)：19-23.

[7]龙 瑞，秦永元，夏家和.CDKF在捷联惯导系统大失准角初始对准的应用[J].西北工业大学学报，2010，28(3)：364-368.

[8]严恭敏，严卫生，徐德民.简化UKF滤波在SINS大失准角初始对准中的应用[J].中国惯性技术学报，2008，16(3)：253-264.

[9]黄凤荣，孙伟强，翁海娜.基于UKF的旋转式SINS大方位失准角初始对准方法[J].中国惯性技术学报，2010，18(5)：513-517.

[10]Gao W，Xu B，Sun H，et al.Application of nonlinear filtering for SINS initial alignment[C].2006 International Conference on Mechatronics and Automation.IEEE，2006：2259-2263.

[11]孙 枫，唐李军.Cubature卡尔曼滤波-卡尔曼滤波算法[J].控制与决策，2012，27(10)：1561-1565.

[12]赵 奇.卡尔曼滤波在GPS定位中的研究与实现[D].成都：电子科技大学.2013.

[13]钱华明，葛 磊，彭 宇.多渐消因子卡尔曼滤波及其在SINS初始对准中的应用[J].中国惯性技术学报，2012，20(3)：287-291.

[14]杨 丹.卡尔曼滤波器设计及其应用研究[D].湘潭：湘潭大学.2014.

[15]杜党波，张 伟，胡昌华，等.含缺失数据的小波-卡尔曼滤波故障预测方法[J].自动化学报，2014，40(10)：2115-2125.

[16]韩 萍，桑威林，石庆研.一种新型非线性卡尔曼滤波方法[J].仪器仪表学报，2015，36(3)：632-638.

[17]李方能，许江宁，亓洪标 基于边缘采样UKF滤波的捷联惯导初始对准方法[J].中国惯性技术学报，2014，22(5)：612-618.

Study on Initial Alignment Method Basedon Central Difference Calman Filter

Jia Heming ，Yang Zewen，Song Wenlong*

(College of Mechanical and Electrical Engineering，Northeast Forestry University，Heilongjiang，Harbin 150040，China)

Because the error model of the strapdown inertial navigation system is of nonlinear characteristics under the established large azimuth misalignment，the Central Difference Kalman Filter (CDKF) method was used to conduct the initial alignment simulation for controlling object of the strapdown inertial navigation system in this paper.Compared with the extended Kalman filter (EKF) and the unscented Kalman filter (UKF)，CDKF would improve the filtering precision of the system image and the objective，and did not need specific models to calculate the analytical equation，which saved the time for computing Jacobian matrix of driven complex constraint equations.The final simulation results demonstrated that the use of CDKF for the optimal estimation of system sate was better than EKF and UKF methods，the CDKF algorithm was of the high precision and convergence and could satisfy the system requirements for navigation under the nonlinear model.

Large azimuth misalignment；strapdown inertial navigation system；initial alignment；CDKF

2016-03-08

中央高校基本科研业务费专项资金资助项目(2572014BB03)；国家自然科学基金(31470714)

贾鹤鸣，博士，副教授。研究方向：非线性系统控制理论与应用、智能控制与滤波技术。

*通信作者：宋文龙，博导，教授。研究方向：控制系统的检测与滤波技术。E-mail：wlsong@126.com

贾鹤鸣，杨泽文，宋文龙.基于中心差分卡尔曼滤波的初始对准方法研究[J].森林工程，2016，32(6)：66-70.

TP 273

A

1001-005X(2016)06-0066-05