钛合金动态本构关系的研究及应用

韩悌信 ， 曾祥国 ， 盛 鹰 ， 陈 军 ，陈华燕

(1.四川大学，四川 成都 610065)(2.北京应用数学与力学研究所，北京 100088)



钛合金动态本构关系的研究及应用

韩悌信1， 曾祥国1， 盛 鹰1， 陈 军2，陈华燕1

(1.四川大学，四川 成都 610065)(2.北京应用数学与力学研究所，北京 100088)

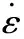
钛合金；S型曲线；修正Johnson-Cook模型；遗传算法

0 引 言

具有优良力学性能和耐腐蚀性能的钛及钛合金被越来越多地应用于航空航天、化工、舰船等领域，也就越来越要求人们了解和掌握其在各种情况下的力学行为。众多研究表明，钛合金是应变率高度敏感材料，且在高应变率下呈现出特殊的力学性能[1]。因此，在涉及高速成形、高速碰撞、动态断裂以及弹塑性波传播等工程应用中，有必要研究钛合金在高应变率下的力学性能[2]。但是，在实际中要得到钛合金在极高应变率、极高温度下的应力、应变数据比较困难，更不可能得到钛合金在所有应变率及温度下的力学性能。一种可行的方法是用相关理论提出的本构关系模型来描述应力与应变率、温度之间的关系，采用实验数据拟合出模型中的待定参数，再以此本构关系来预测材料在任意应变率及温度下的力学行为。

Johnson-Cook模型形式简单、各参数含义清晰、易拟合，被广泛用于描述金属材料的力学行为，且已被众多商用有限元软件所采用，用于结构或构件在动态载荷作用下的动力学有限元分析[3-6]。但经典的Johnson-Cook模型不能很好地描述钛合金在高应变率下的力学性能。这是因为在高应变率下，钛合金内部温升会影响流变应力的大小，即温升会减弱应变、应变率的强化效应。为此，众多学者对Johnson-Cook模型进行了修正，以更好地描述钛合金在高应变率下的力学行为。

1 修正的Johnson-Cook模型

经典Johnson-Cook模型考虑了加工硬化效应、应变率强化效应和温度软化效应，被广泛用来描述金属材料的塑性变形行为，其表达式为[8]：

(1)

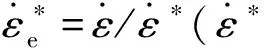
在102～105s-1下，钛合金往往表现出热粘塑性，其内部温升会影响本构关系中的流变应力σp，而经典的Johnson-Cook模型很难描述材料在高应变率下的粘塑性行为[9]，因此需对其修正。当材料经历由εp1到εp2的塑性应变时，其内部的温升ΔT及流变应力变化量Δσp由下式决定[1]：

(2)

式中β为功热转换系数，ρ为材料密度，Cp为材料的比热容。

(3)

式中，k1、k2为材料常数，且k1>1,k2>0，需要通过实验数据来确定。

(4)

2 修正的Johnson-Cook模型的常数确定

2.1 常数拟合

人们确定Johnson-Cook模型中的材料参数时，一般都是从特殊的实验曲线出发，逐个确定待定参数，这样做的弊端是忽略了不同应变率下的实验数据对本构参数的影响，而使用最小二乘法并考虑所有试验曲线的枚举法则计算效率太低。因此希望找到一种算法，既能考虑多条实验数据之间的影响，又能大大减小计算量，而遗传算法正好可以满足这一要求。遗传算法[11](GA)模拟了自然选择和遗传中发生的复制、交叉和变异等现象，从任一初始群体出发，通过随机选择、交叉和变异操作，产生一群更适应环境的个体，使群体进化到搜索空间中越来越好的区域，这样一代一代地不断繁衍进化，最后收敛到一群最适应环境的个体，从而求得问题的最优解。

修正的Johnson-Cook模型中有A、B、n0、C、m、K 、k1、k2共8个待定参数，不妨令X=[A，B，n0，C，m，K，k1，k2]T，则目标函数为：

(5)

考虑多组实验数据点(εpi,σpi)(i=1,2,…,n)，以式(5)为目标函数，采用2.1节中介绍的遗传算法对式(4)中的8个材料参数进行求解。各变量需给定搜索域：

A∈[Amin,Amax]；B∈[Bmin,Bmax]；

n0∈[n0min,n0max]；C∈[Cmin,Cmax]；

m∈[mmin,mmax]；K∈[Kmin,Kmax]；

k1∈[k1min,k1max]；k2∈[k2min,k2max]。

至此，修正Johnson-Cook模型中的8个材料常数已全部确定，方程为：

(6)

2.2 修正的Johnson-Cook模型的增量形式

修正的Johnson-Cook模型式(6)适用于描述钛合金在任意应变率及温度下的本构关系。Johnson-Cook模型表示的是流变应力与塑性应变、应变率、温度之间的关系，而最终想要得到的是真应力-真应变曲线，因此，需要采用应力增量法求得特定真应力下的真应变，具体步骤如下。

当真应力>屈服应力时，修正后的真应力为：

(7)

对式(7)两边取增量：

(8)

则应力增量迭代的表达式为：

(9)

式中，n表示增量步开始时的值，n+1表示增量步结束时的值。

根据式(8)、式(9)，可以得到钛合金在应力控制条件下，在不同应变率及温度下的真应力-真应变曲线，然后可以将这些曲线与实验数据进行对比。

3 Ti-6Al-4V合金本构模型算例

3.1 Ti-6Al-4V合金动态本构方程

Ti-6Al-4V合金的Tm=1 933 K，E=107 800 MPa。基于文献[7]中不同应变率及温度下的流变应力-塑性应变数据，采用本文提出的修正的Johnson-Cook模型及参数求解方法，得到Ti-6Al-4V合金的本构参数，如表1所示。根据参考文献[7]中的结果，给定各变量的搜索域为：

A∈[500,2 000]；B∈[600,1 500]；

n0∈[0.01,0.99]；C∈[0.01,0.02]；

m∈[0.6,0.8]；K∈[-1,1]；

k1∈[10,2 000]；k2∈[0,0.01]。

表1 修正的Johnson-Cook模型中Ti-6Al-4V合金的本构参数

(10)

图的函数图Fig.2 Function image of β

图3 β曲线斜率图Fig.3 Slope image of β curve

修正的Johnson-Cook模型适用于任意应变率及温度下钛合金的本构关系。代入表1所给出的Ti-6Al-4V合金的本构参数，得式(11)：

(11)

3.2 Ti-6Al-4V合金的真应力-真应变曲线

由式(11)可得：

(12)

低应变率、不同温度下，Ti-6Al-4V合金的6组真应力-真应变曲线(10-5s-1、296 K；10-3s-1、296 K；1 s-1、296 K；10-3s-1、422 K；10-3s-1、588 K；10-3s-1、755 K)的实验值(文献[7])和本文计算值的比较如图4所示。

图4 低应变率、不同温度下Ti-6Al-4V合金真应力-真应变曲线的实验值和本文计算值比较Fig.4 Comparison of true stress-true strain curves of experiment and calculation at low strain rates for various temperatures for Ti-6Al-4V alloy

高应变率、不同温度下，Ti-6Al-4V合金的4组真应力-真应变曲线(3 700 s-1、998 K；、3 100 s-1、798 K；2 700 s-1、598 K； 1 900 s-1、296 K)的实验值(文献[7])和本文计算值的比较如图5所示。

图5 高应变率、不同温度下Ti-6Al-4V合金真应力-真应变曲线的实验值和本文计算值比较Fig.5 Comparison of true stress-true strain curves of experiment and calculation at high strain rates for various temperatures for Ti-6Al-4V alloy

从图4和图5可以看出，高应变率下给定应变的流变应力明显高于低应变率下的，且应变率越高，给定应变下的流变应力越大，动态屈服强度也随应变率的增加而增大，说明Ti-6Al-4V合金是一种应变率敏感材料。低应变率下的流变应力随应变增大逐渐升高，表现出明显的应变强化效应，而高应变率下的流变应力在应变超过一定值后逐渐停止升高，甚至有下降的趋势。这表明，低应变率下的应变强化效应强于应变率强化效应，高应变率下的应变率强化效应强于应变强化效应，绝热温升是影响流变应力的主要因素，绝热温升引起流变应力的改变量抵消了应变强化引起的流变应力增量。由低应变率下的真应力-真应变曲线(图4)可知，在同一应变率下，变形温度越高，给定应变下的流变应力越低，表明Ti-6Al-4V合金具有温度软化效应，高应变率下的绝热温升引起的流变应力降低也证实了这一点。修正的Johnson-Cook模型可以很好的描述Ti-6Al-4V合金的力学行为，既符合低应变率下的实验结果，也符合高应变率下的实验结果。

4 结 论

(2)用遗传算法拟合本构方程参数，这种拟合方法可信度高，且具有普遍意义。

(3)经过Ti-6Al-4V合金算例验证，修正的Johnson-Cook模型适用于任何应变率及任何温度下描述钛合金力学行为，并对预测材料在高应变率、高温下的力学行为具有重要的工程意义。

[1] 刘旭阳. TC4钛合金动态本构关系研究[D]. 南京:南京航空航天大学, 2010.

[2] 徐天平,王礼立,卢维娴. 高应变率下钛合金Ti-6Al-4V的热-粘塑性特性和绝热剪切变形[J]. 爆炸与冲击, 1987,7(1): 1-8.

[3] 汤铁钢, 刘仓理. 高应变率拉伸加载下无氧铜的本构模型[J]. 爆炸与冲击, 2013,33(6): 581-586.

[4] 汤铁钢, 李庆忠, 陈永涛, 等.实现材料高应变率拉伸加载的爆炸膨胀环技术[J]. 爆炸与冲击, 2009, 29(5): 546-549.

[5] 汤铁钢, 刘仓理. 一种新型爆炸膨胀环实验装置[J]. 实验力学, 2013, 28(2): 247-254.

[6] 曾祥国, 盛鹰，韩悌信，等. 考虑热粘塑性钛合金动态本构关系及其实验验证[J]. 四川大学学报(工程科学版), 2014,46(6): 152-157.

[7] Khan A S, Suh Y S, Kazmi R. Quasi-static and dynamic loading responses cand onstitutive modeling of titanium alloys[J]. International Journal of Plasticity, 2004, 20(12): 2233-2248.

[8] 曾祥国,陈华燕,胡益平. 工程弹塑性力学[M]. 成都:四川大学出版社, 2013.

[9] 杨扬,曾毅,汪冰峰. 基于Johnson-Cook模型的TC16钛合金动态本构关系[J]. 中国有色金属学报, 2008,18(3): 505-510.

[10] 严慧吕, 效国南. S 型曲线自回归模型的自回归分析[J]. 高等函授学报: 自然科学版, 2010, 23(5): 95-96.

[11] 周明,孙树栋. 遗传算法原理及应用[M]. 北京:国防工业出版社, 1999: 1-202.

Study and Application of Dynamic Constitutive Relation for Titanium Alloy

Han Tixin1,Zeng Xiangguo1,Sheng Ying1,Chen Jun2,Chen Huayan1

(1.Sichuan University, Chengdu 610065,China)(2.Institute of Applied Physics and Computational Mathematics, Beijing 100088,China)

titanium alloy; S-curve; modified Johnson-Cook model; genetic algorithm

2016-06-05

国防重点基金项目(B1520132013-1)

曾祥国(1960—)，男，教授。

TG146.2+3

A

1009-9964(2016)04-0017-05