创新网络与输出型开放式创新关系的实证

崔海云

一、文献回顾与假设提出

1.创新网络“结构洞”与输出型开放式创新之间的关系。输出型开放式创新是指企业向外部“释放”、授权或者出售创新信息和技术知识，实现创新成果商业化的创新模式。企业通过主动地溢出或者出售“于己无用”的冗余技术知识给其他组织，不仅可以缓解自身进行创新成果商业化的压力，而且还可以获得可观的技术转让收益。根据企业向外部输出知识的过程中是否存在经济交易，输出型开放式创新可分为授权和免费释放两种。授权是指企业通过将自身的研发成果出售或者授权给其他组织的方法，来实现新创技术和创意的商业化的过程。免费释放是指企业将内部的技术知识、创新信息和资源无偿输出到外部环境中，而不追求任何直接的经济回报。

企业的创新绩效受到其在创新网络的结构洞的影响（Burt，2004；Zaheer &Soda，2009；Insead A V S.，2006；Shipilov & Li，2008）。“结构洞”是指社会网络中的“洞隙”，这些“洞隙”的存在导致网络中的行为主体之间不能直接建立连接或者行为主体之间的关系出现中断（Burt，1992）。一些学者认为，结构洞能够为网络中的聚焦节点带来信息优势和控制优势：一方面，结构洞是信息流动的缺口，占据结构洞的网络节点企业更有可能获取更棒的新创意、更多的异质性信息（Gargiulo et al，2009）。另一方面，“结构洞”企业可以凭借自身的“中介”地位和信息优势，扮演网络中信息交换的搭桥机构或组织。横跨不同企业间的“结构洞”可以使网络节点企业获得操纵其他互不相连企业之间信息流动的优势，进而迫使它们让步或者竞争（Burt，1997）。

笔者认为，输出型开放式创新不仅可以缓解企业自身进行创新成果商业化的压力，而且还“激活”了大量被企业闲置的“无用”技术，为企业获得更多的研发回报。创新网络的结构洞有利于企业准确识别和甄选技术需求方，推动技术快速转移。因此，在企业的输出型开放式创新过程中，合理占据创新网络的结构洞并对其科学管理将有利于快速、有效地实现企业技术成果的外部商业化。基于此，本文提出如下假设：

假设la预期 创新网络结构洞对授权具有正向的促进作用。

假设lb预期 创新网络结构洞对免费释放具有正向的促进作用。

2.创新网络强联系及其中介作用。强联系（strong ties）是某一联系中所包含的频繁的、亲密的、互惠的联系状态（Reagans & McEvily，2003；Lechner et al.，2010）。强联系对企业创新绩效的积极作用主要体现在三方面：第一，强联系有利于促进信任的形成，增强合作伙伴转移知识的意愿，促进复杂与缄默知识在组织之间的有效转移（McEvily & Marcus，2005）。第二，强联系能够有效地抑制合作伙伴的机会主义行为（Dyer & Nobeoka，2000），降低合作伙伴之间的冲突水平，提升知识分享的效率。第三，强联系有利于形成共同解决问题的意愿和机制，促进合作伙伴柔性地解决问题（Uzzi，1997）。

笔者认为，企业与创新网络其他成员之间的强联系能够修补创新网络结构洞造成的沟通“洞隙”，有助于增进网络中成员间的信任和互惠关系，降低知识转移的不确定性和风险，推动技术知识（特别是复杂的隐性知识）的转移和扩散，为企业顺利开展输出型开放式创新创造良好条件。基于此，本文提出如下假设：

假设2a预期 强联系在创新网络结构洞与授权的关系中扮演中介变量角色。

假设2b预期 强联系在创新网络结构洞与免费释放的关系中扮演中介变量角色。

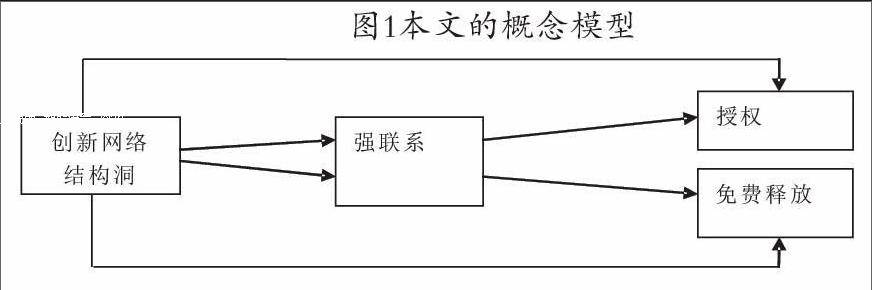
综上所述，本文的研究框架如图1所示。

二、研究设计

1.样本选取与数据收集。数据收集包括两个阶段：预调研阶段（2014年7月）和正式调研阶段（2014年8月～2014年10月）。本次调研一共发放问卷300份，回收问卷237份，有效问卷226份，回收率79%，有效率75.3%。

2.变量测量。①因变量：输出型开放式创新。本项研究借鉴了Lichtenthaler（2009）和陈钰芬（2008）等学者的研究成果。“授权”包括2个题项：a.贵公司经常出售专利或者进行专利授权。b.贵公司只出售或对外授权那些非核心技术。“免费释放”包括2个题项：a.贵公司经常主动到其他企业进行创新项目的介绍和报告。b.贵公司愿意为其他企业或组织的创新工作提供建议和帮助。②自变量：结构洞。学者们通常用“控制信息流的能力”来测度结构洞。“创新网络结构洞”包括2个题项：a.创新网络内的其他企业之间的技术交流必须经过贵公司。b.贵公司在外部创新网络内拥有一定的地位和影响力。③中介变量：强联系。本文参照了Hansen（1999）和Reagans & McEvily（2003）的测量方法，“强联系”包括2个题项：a.贵公司与外部网络合作伙伴联系很频繁。b.贵公司与外部网络合作伙伴的关系很亲密。④控制变量。为了保证研究结果的可靠性和有效性，本文将企业规模、企业年龄和企业家精神作为控制变量处理。本次调查均采用Likert7分量表。

三、 实证分析和假设检验

1.信度与效度分析。本项研究采用因子分析检验变量测量的信度与效度。因子分析结果表明，各题项都落在预设的因子上，并且因子载荷均在0.7以上，表示变量测量具有较好的聚合效度与区分效度。结构洞、免费释放的Cronbachs α系数略低（分别为0.793、0.786），但仍然在可接受范围之内。强联系、授权的Cronbachs α系数均在0.8以上（分别为0.812、0.832），可知数据具有良好的信度。上述分析表明本项研究的变量具有较好的效度和信度，适宜进一步做回归分析与假设检验。

2.描述性统计与相关系数。强联系与结构洞的相关系数是0.092，授权与结构洞、强联系的相关系数分别是0.259、0.193，免费释放与结构洞、强联系、授权的相关系数分别是0.213、0.203、-0.082。

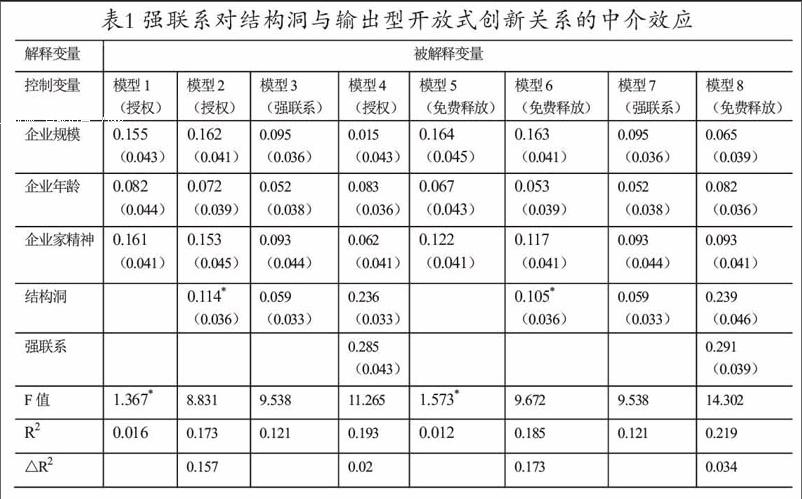
3.回归分析及假设检验。本研究运用层次回归法对研究假设进行检验。在检验变量是否具有中介效应时，我们采用Baron和Kenny（1986）以及温忠麟等人（2004）所建议的方法。分析结果如表1所示。

模型1是输出型开放式创新（授权）对控制变量的回归。模型2是输出型开放式创新（授权）同时对控制变量和自变量（结构洞）做回归（回归系数显著，p<0.05），模型的F值明显增大，因此，与模型1相比，模型2增加解释变量（结构洞）后，模型拟合度得以优化，R2也增大，R2增加了15.7%（p<0.05），表明结构洞对输出型开放式创新（授权）具有一定的解释作用。假设1a得到支持。

模型3是中介变量（强联系）对解释变量（结构洞）做回归（回归系数不显著，p>0.1）。模型4是输出型开放式创新（授权）同时对解释变量（结构洞）和中介变量（强联系）做回归（回归系数显著，p<0.05），模型的F值明显增大，与模型2 相比，R2也增大，R2增加了2%（p <0.05）。也就是说，模型4在模型2的基础上增加中介变量（强联系）后，对输出型开放式创新（授权）的解释能力迅速提升。在模型4中，输出型开放式创新（授权）对解释变量（结构洞）和中介变量（强联系）的回归系数显著（p <0.05）。由于模型3中的中介变量（强联系）对解释变量（结构洞）的回归系数不显著，而模型4中的输出型开放式创新（授权）对中介变量（强联系）的回归系数显著，根据温忠麟等人（2004）的建议，需要进行Sober检验。Sober检验（双尾）的统计值为2.291（p<0.05），说明Sober检验的效应显著，因而，强联系在结构洞和输出型开放式创新（授权）之间的中介效应得到支持。假设2a得到支持。

模型5是输出型开放式创新（免费释放）对控制变量的回归。模型6是输出型开放式创新（免费释放）同时对控制变量和自变量（结构洞）做回归（回归系数显著，p<0.05），模型的F值明显增大，因此，与模型5相比，模型6增加解释变量（结构洞）后，模型拟合度得以优化，R2也增大，R2增加了17.3%（p<0.05），表明结构洞对输出型开放式创新（免费释放）具有一定的解释作用。假设1b得到支持。

模型7是中介变量（强联系）对解释变量（结构洞）做回归（回归系数不显著，p>0.1）。模型8是输出型开放式创新（免费释放）同时对解释变量（结构洞）和中介变量（强联系）做回归（回归系数显著，p<0.05），模型的F值明显增大，与模型6相比，R2也增大，R2增加了3.4%（p<0.05）。也就是说，模型8在模型6的基础上增加中介变量（强联系）后，对输出型开放式创新（免费释放）的解释能力迅速提升。在模型8中，输出型开放式创新（免费释放）对解释变量（结构洞）和中介变量（强联系）的回归系数显著（p<0.05）。由于模型7中的中介变量（强联系）对解释变量（结构洞）的回归系数不显著，而模型8中的输出型开放式创新（免费释放）对中介变量（强联系）的回归系数显著，根据温忠麟等人（2004）的建议，需要进行Sober检验。Sober检验（双尾）的统计值为2.256（p<0.05），说明Sober检验的效应显著，因而，强联系在结构洞和输出型开放式创新（免费释放）之间的中介效应得到支持。假设2b得到支持。

本文以科技型企业作为样本实证检验了强联系在创新网络结构洞与输出型开放式创新之间的关系中发挥的中介作用。实证研究结果表明，强联系在创新网络结构洞与输出型开放式创新的关系之间扮演中介变量角色。[基金项目：北京物资学院高级别科研项目培育基金（GJB20164002）]

（作者单位：北京物资学院商学院）